[leetcode hot 150]第一百零八题,将有序数组转换为二叉搜索树
题目:给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵
平衡二叉搜索树。
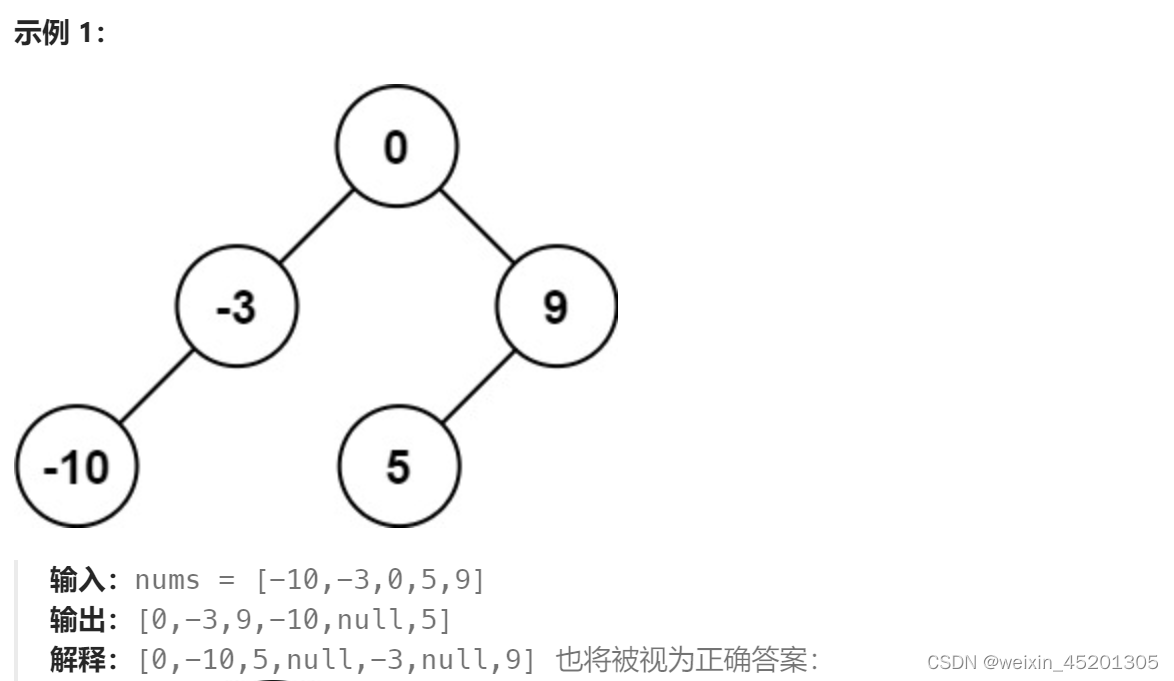
给定一个有序的整数数组,我们需要构建一棵平衡的二叉搜索树。平衡二叉树是指任意一个节点的左右子树的高度差不超过1。
由于给定的数组是有序的,可以利用这个特性来构建二叉搜索树。可以选择数组中间的元素作为根节点,然后递归地构建左子树和右子树。
public class no_108 {public static void main(String[] args) {int[] arr = {-10, -3, 0, 5, 9};TreeNode treeNode = sortedArrayToBST(arr);}public static TreeNode sortedArrayToBST(int[] nums) {return buildTree(nums, 0, nums.length - 1);}public static TreeNode buildTree(int[] nums, int left, int right) {if (left > right) return null;int mid = left + (right - left) / 2;TreeNode root = new TreeNode(nums[mid]);root.left = buildTree(nums, left, mid - 1);root.right = buildTree(nums, mid + 1, right);return root;}
}
利用有序数组的特点,将树构建出来。
相关文章:

[leetcode hot 150]第一百零八题,将有序数组转换为二叉搜索树
题目:给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡二叉搜索树。 给定一个有序的整数数组,我们需要构建一棵平衡的二叉搜索树。平衡二叉树是指任意一个节点的左右子树的高度差不超过1。 由于给定的数组是有序的…...

科普丨什么是数字孪生灌区(平台)?如何建设?有何好处?
在农业发展的新时代,数字孪生灌区的概念逐渐走进大众视野,成为推动农业现代化、提升粮食安全保障能力的关键力量。那么,究竟什么是数字孪生灌区?它又是如何建设的?又能为我们带来哪些好处呢? 数字孪生灌区…...

Python爬虫如何入门:一步步走向精通的指南
Python爬虫如何入门:一步步走向精通的指南 在信息爆炸的时代,爬虫技术已经成为获取、整理和分析数据的必备技能。Python,以其简洁易懂的语法和强大的库支持,成为了爬虫开发的热门语言。那么,如何入门Python爬虫呢&…...

Linux用户和用户组的操作
用户管理 以Tom做为用户名 以dev做为用户组 增加用户 sudo adduser Tom #不建议使用useradd/userdel系列的命令删除用户 sudo deluser Tom --remove-home # 删除Tom用户及home目录 重置密码 sudo passwd Tom加入用户组 sudo usermod -a -G dev Tom # sudo usermod -aG …...
)
git命令行分支(增删改查)
文章目录 一、创建分支并推送到远程仓库二、拉取指定分支代码三、删除分支 一、创建分支并推送到远程仓库 初始化git git init如果有远程仓库就进行克隆远程仓库 origin 表示远程仓库地址 git clone origin# 如果没有远程仓库 就进行创建一个远程仓库 git remote add origin ht…...

地理加权回归GWR简介
地理加权回归GWR简介 一、定义: 地理加权回归(Geographically Weighted Regression,简称GWR)是一种空间数据分析方法,专门用于处理空间异质性(spatial heterogeneity)问题。以下是对GWR的详细简…...
康谋技术 | 自动驾驶:揭秘高精度时间同步技术(一)
众所周知,在自动驾驶中,主要涵盖感知、规划、控制三个关键的技术层面。在感知层面,单一传感器采集外界信息,各有优劣,比如摄像头采集信息分辨率高,但是受外界条件影响较大,一般缺少深度信息&…...
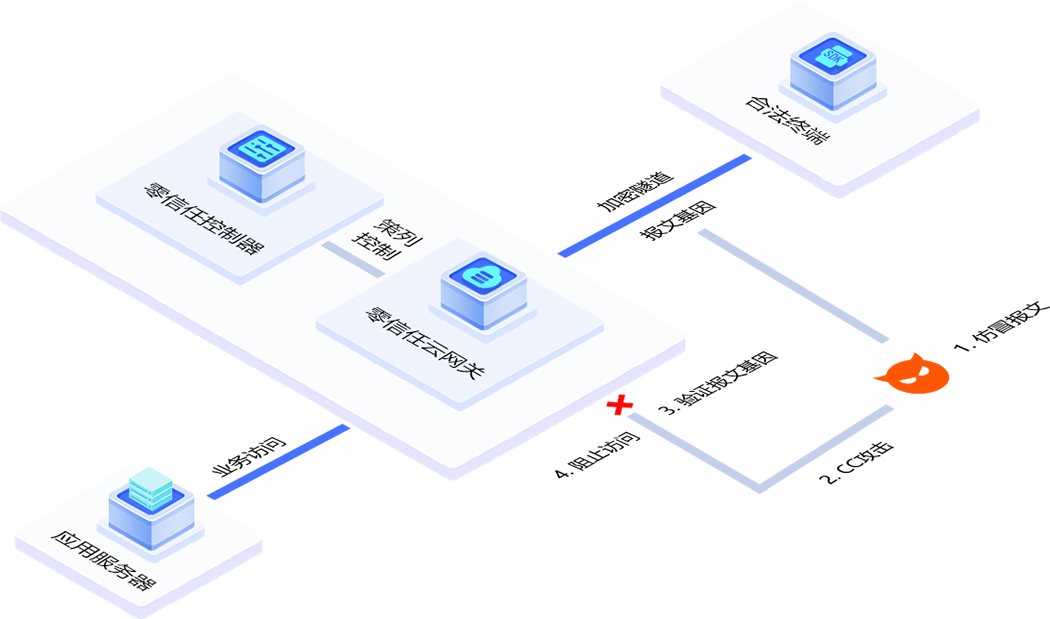
客户端被攻击怎么办,为什么应用加速这么适合
随着科技的进步和互联网的普及,游戏行业也正在经历前所未有的变革。玩家们不再满足于传统的线下游戏,而是转向了线上游戏。然而,随着游戏的线上化,游戏安全问题也日益凸显。游戏受到攻击是游戏开发者永远的痛点,谈“D“…...

Introduction to HAL3
目录 HAL3 behavior Overview of HAL1 v.s HAL3 HAL3 behavior: HAL3 - detail: HAL3 operation and pipeline Framework Diagram Problem of current code Operation mode Full v.s limited Do: Don’t: Metadata Manual control – ISP control...

Vue02-搭建Vue的开发环境
一、Vue.js的安装 1-1、直接用 <script> 引入(CDN) 1、CDN的说明 2、Vue的版本说明 生产版本是开发版本的压缩。 3、Vue的引入 验证是否存在Vue函数: 4、搭建Vue的开发环境 ①、下载开发版本的Vue,并在代码中引入 ②、安…...

Python | 句子缩写
字符串大小的比较Unicode码值 类似于asc|| 码 小写字母从 a 到 z 对应的 Unicode 码值是从 97 到 122,而大写字母从 A 到 Z 对应的 Unicode 码值是从 65 到 90, 大小写字母之间的差值为32,所以可以通过数学运算将小写字符减去32后转换为大写字符。 字…...
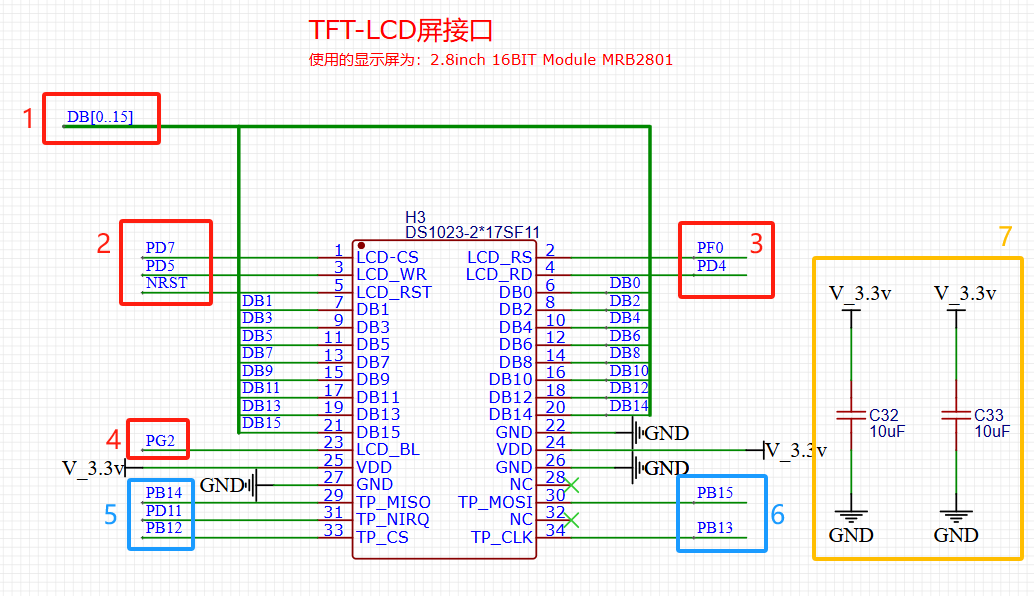
STM32自己从零开始实操04:显示电路原理图
一、TFT-LCD 屏接口 1.1指路 以下是该部分的设计出来后的实物图,我觉得看到实物图可能更方便理解这部分的设计。 图1 实物图 这部分设计的是一个屏幕的接口,很简单。使用的屏幕是:2.8inch 16BIT Module MRB2801。 1.2数据手册 ࿰…...

数分—AB测试
一、介绍 AB测试是一种常用于比较两种或多种不同版本的产品、服务或策略效果的实验方法。在AB测试中,被比较的版本被标记为A组和B组,然后两组被随机分配给不同的用户群体或实验对象。接着,针对每个组收集数据,比如用户行为、转化…...
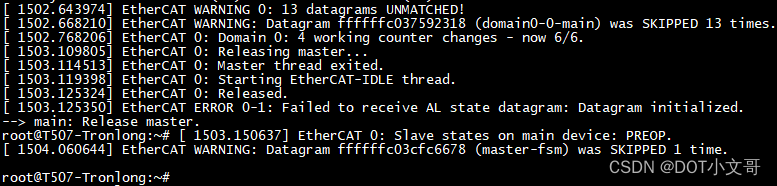
基于全志T507-H的Igh EtherCAT主站案例分享
基于全志T507-H的Linux-RT IgH EtherCAT主站演示 下文主要介绍基于全志T507-H(硬件平台:创龙科技TLT507-EVM评估板)案例,按照创龙科技提供的案例用户手册进行操作得出测试结果。 本次演示的开发环境: Windows开发环…...
)
刷题记录(20240605)
1.数组构造 题目描述 小红的数组构造小红希望你构造一个数组满足以下条件: 1.数组共有 n个元素,且所有元素两两不相等。 2.所有元素的最大公约数等于 k。 3.所有元素之和尽可能小。请你输出数组元素之和的最小值。 输入描述: 两个正整数 n 和 k。 输出描述ÿ…...

CUDA和OpenGL纹理texture结合
cuda和OpenGL纹理结合,并进行直方图计算 针对于单通道16位图像。结合方式在CUDA_equalizeHistogram_16函数中。 其他的为CUDA核函数。 #define HISTOGRAM_LENGTH 65536 // 2^16 表示16位深度定义直方图长度为65536,对应16位像素值的范围(0-65535)。 __global__ void com…...
市场凌乱,智能算法哪种效果好?
当我们在面对市场波动,个股震荡,无从下手的时候,不懂算法的朋友就只懂做t;懂算法的朋友这会儿就迷茫并不知道选择哪种智能算法交易?今天小编给大家整理一套性价比高的,适合个人投资者搞的算法交易ÿ…...

学会这14大招,30天涨粉两三千没问题!沈阳新媒体运营培训
很多小白在刚转入公司做新媒体时,基本都是从帮助公司运营账号开始的。但不同于个人号,一个企业本身是没有ip属性的,它的风格、调性等,都需要通过你的运营,让它变成一个活灵活现的、赋予独立个性人设的账号。 目前&…...

SQL数据库性能优化
1.查询尽量避免使用select * 1.1 增加磁盘开销:数据库本质上是将记录存储在磁盘上,查询操作就是一种进行磁盘IO的行为,我们查询的字段越多,读取的内容也就越多,对IO磁盘的开销也就会增大,特别是某些字段,如…...

eNSP学习——RIP路由协议基础配置
目录 主要命令 原理概述 实验内容 实验目的 实验拓扑 实验编址 实验步骤 1、基本配置 2、使用RIPv1搭建网络 开启 RIP调试功能 3、使用RIPv2搭建网络 RIPv1和RIPv2的不同 需要eNSP各种配置命令的点击链接自取:华为eNSP各种设备配置命令大全PD…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
