【docker】docker的安装
如果之前安装了旧版本的docker我们需要进行卸载:
卸载之前的旧版本
卸载
# 卸载旧版本
sudo apt-get remove docker docker-engine docker.io containerd runc
# 卸载历史版本
apt-get purge docker-ce docker-ce-cli containerd.io docker-buildx-plugin docker-compose-plugin docker-ce-rootless-extras -y
# 删除docker目录
rm -rf /var/lib/docker
rm -rf /var/lib/containerd
安装docker
配置docker下载源
#curl 命令安装
sudo apt install curl -y
#创建 gpg key 目录
sudo mkdir -m 0755 -p /etc/apt/keyrings
#下载 gpg key
curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo gpg --dearmor --yes -o /etc/apt/keyrings/docker.gpgecho \
"deb [arch=$(dpkg --print-architecture) signedby=/etc/apt/keyrings/docker.gpg] https://download.docker.com/linux/ubuntu \
$(lsb_release -cs) stable" | sudo tee /etc/apt/sources.list.d/docker.list > /dev/null# 写到了/etc/apt/sources.list.d/文件内,下面可以查看验证。
cat /etc/apt/sources.list.d/docker.list
安装docker
apt-get update
apt-get install docker-ce docker-ce-cli containerd.io docker-buildx-plugin docker-compose-plugin -y
配置自动启动
#配置加载
sudo systemctl daemon-reload
#启动服务
sudo systemctl start docker
#开启启动 --> 开机自启
sudo systemctl enable docker
#查看服务状态
sudo systemctl status docker
验证docker是否运行成功
# 检测是否运行成功
docker run hello-world
# 检查安装版本
docker version
docker安装不上 提示NO_PUBKEY:
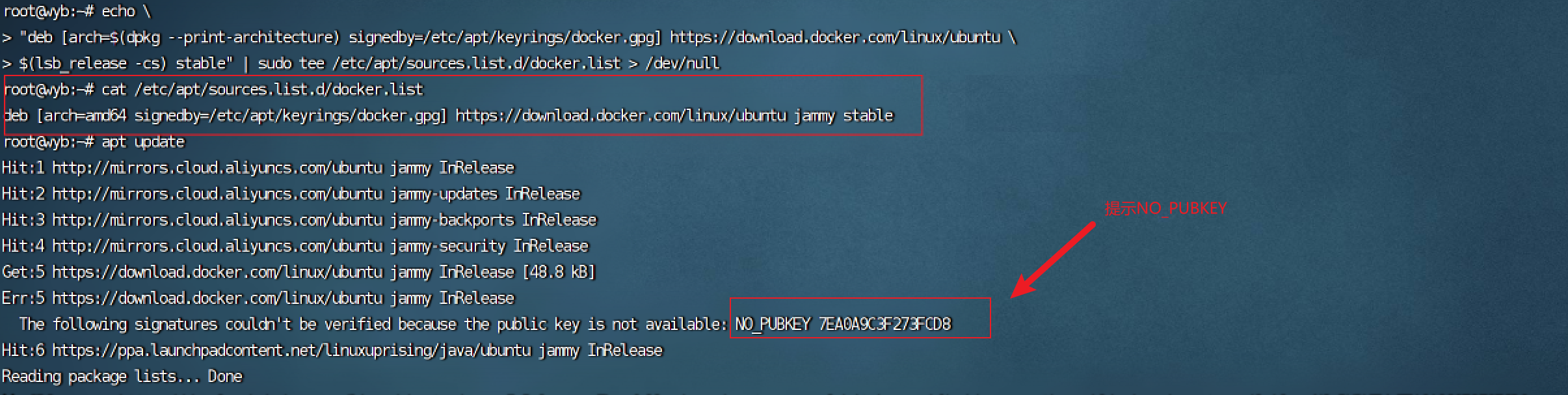
# 手动验证 xxxxx 就是 提示的 NO_PUBKEY
apt-key adv --keyserver keyserver.ubuntu.com --recv-keys xxxxx
安装docker-compose
# docker-compose 的安装
apt install docker-compose
# 检验 docker-compose 是否安装成功
docker-compose
相关文章:

【docker】docker的安装
如果之前安装了旧版本的docker我们需要进行卸载: 卸载之前的旧版本 卸载 # 卸载旧版本 sudo apt-get remove docker docker-engine docker.io containerd runc # 卸载历史版本 apt-get purge docker-ce docker-ce-cli containerd.io docker-buildx-plugin docker…...
OC IOS 文件解压缩预览
热很。。热很。。。。夏天的城市只有热浪没有情怀。。。 来吧,come on。。。 引用第三方库: pod SSZipArchive 开发实现: 一、控制器实现 头文件控制器定义: // // ZipRarViewController.h // // Created by carbonzhao on 2…...

python-web应用程序-Django-From组件
python-web应用程序-Django-From组件 添加用户时 原始方法(本质)【麻烦】 def user_add(req):if req.method GET:return render(req,XXX.html)#POST请求处理:XXXXX-用户数据没有校验 -出现错误提示 -页面上的每一个字段都需要我们重新写一遍 -关联数…...

K8s(Kubernetes)常用命令
大家好,当谈及容器编排工具时,Kubernetes(常简称为K8s)无疑是当今最受欢迎和广泛使用的解决方案之一。作为一个开源的容器编排平台,Kubernetes 提供了丰富的功能,可以帮助开发人员和运维团队管理、部署和扩…...

C#-for循环语句
for循环语句 语法: for(初始化变量; 判断条件; 增量表达式) { // 内部代码 } 第一个空(初始表达式): 一般用来声明一个临时的局部变量 用来计数第二个空(条件表达式): 表明进入循环的条件 一个bool类型的值(bool类型 条件表达式 逻辑运算符)第三个空(增量表达式): 使用第一个空…...

css动画案例练习之会展开的魔方和交错的小块
这里写目录标题 一级目录二级目录三级目录 下面开始案例的练习,建议第一个动手操作好了再进行下一个一、交错的小块效果展示1.大致思路1.基本结构2.实现动态移动 2.最终版代码 二、会展开的魔方1.大致思路1.基本结构;2.静态魔方的构建3.让静态的魔方动起来 2.最终版…...
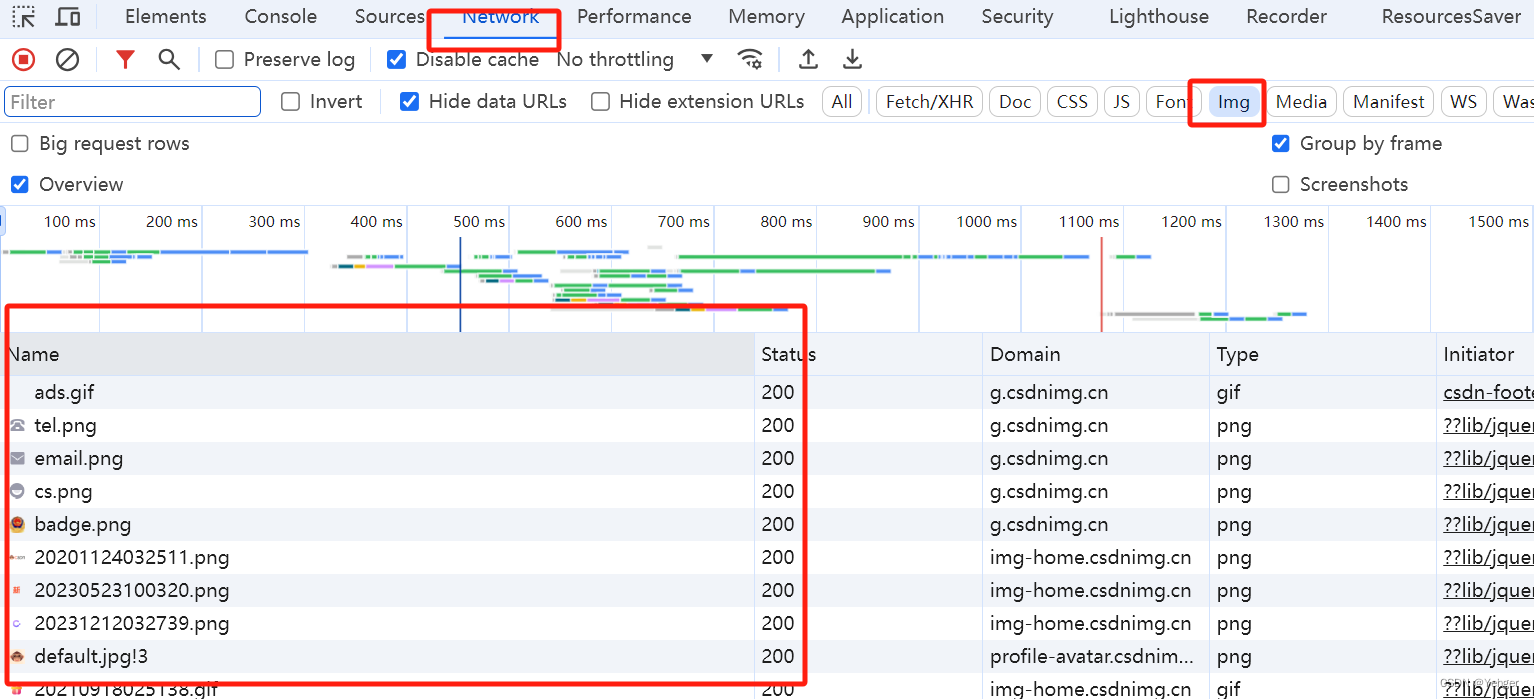
前端逆向之下载canvas引用的图片
前端逆向之下载canvas引用的图片 一、来源二、解决三、如果在Network这里也找不到呢? 一、来源 当我们用dom检查器的时候无法选中想要扒下来的图片,只能选中canvas,这种时候该怎么办呢? 二、解决 这个时候应该换个脑子…...

深度学习手撕代码题
目录: PyTorch实现注意力机制、多头注意力与自注意力Numpy广播机制实现矩阵间L2距离的计算Conv2D卷积的Python和C++实现Numpy实现bbox_iou的计算Numpy实现FocallossPython实现nms、softnmsPython实现BN批量归一化PyTorch卷积与BatchNorm的融合分割网络损失函数Dice Loss代码实…...
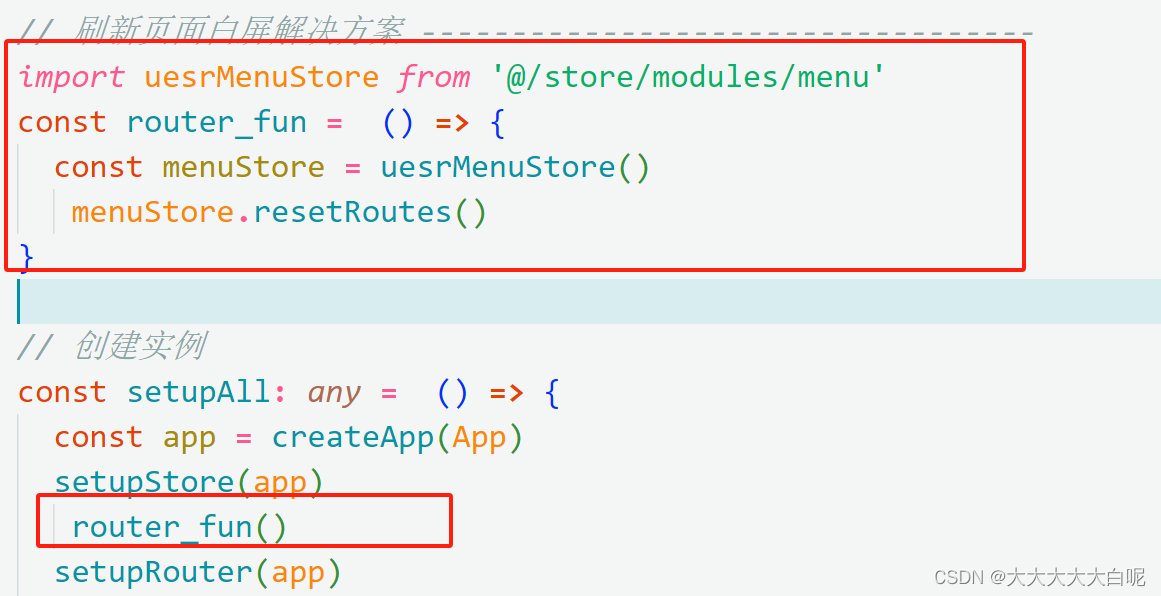
vue3 + ts 动态添加路由,刷新页面白屏问题解决方案
1、store 中添加路由的方法 2、main.ts中使用该方法 然后就可以任意刷新页面了,有问题可以随时滴我...........

【Kubernetes】k8s的调度约束(亲和与反亲和)
一、调度约束 list-watch 组件 Kubernetes 是通过 List-Watch 的机制进行每个组件的协作,保持数据同步的,每个组件之间的设计实现了解耦。 用户是通过 kubectl 根据配置文件,向 APIServer 发送命令,在 Node 节点上面建立 Pod 和…...

Java数据结构- Map和Set
目录 1. Map和Set2. Map的使用3. Set的使用 1. Map和Set Java中,Map和Set是两个接口,TreeSet、HashSet这两个类实现了Set接口,TreeMap、HashMap这两个类实现了Map接口。 带Tree的这两个类(TreeSet、TreeMap)底层的数…...
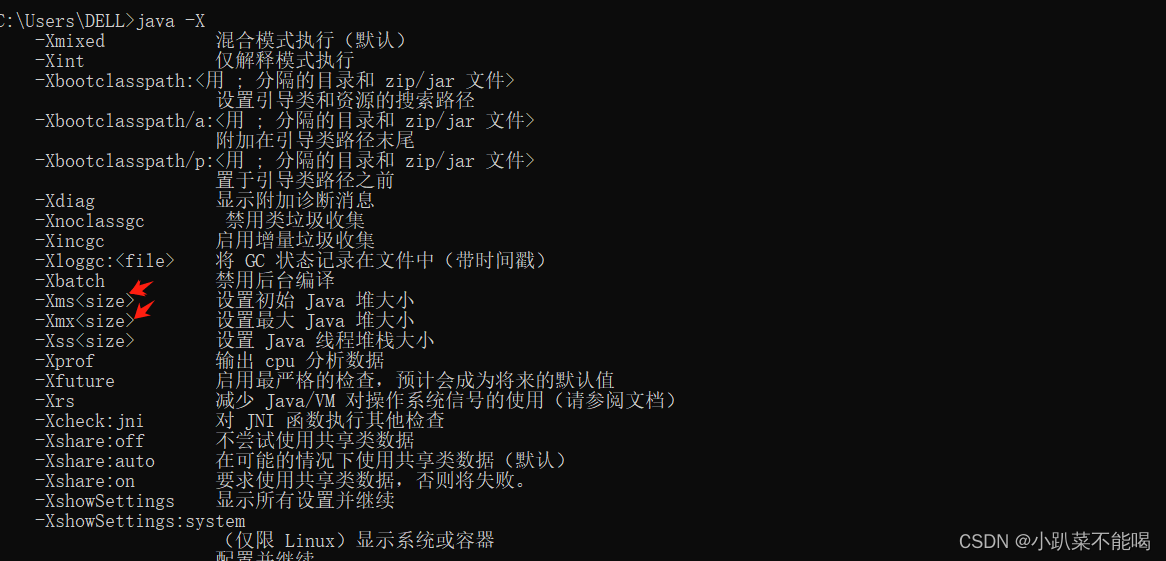
JVM参数配置
JVM参数的三种表示方法 在jvm中,jvm虚拟机参数有以下三种表示方法: 标准参数(-)所有的JVM实现都必须实现这些参数的功能,而且向后兼容非标准参数(-X),默认jvm实现这些参数的功能&…...

Vue 实现的精彩动画效果
在 Vue 开发中,我们可以利用<transition>组件来打造各种令人惊艳的动画效果。下面来详细看看这些有趣的动画效果及其实现代码。 一、缩放类效果 zoom-in(整体放大进入) <template><div><button click"isShow ! …...
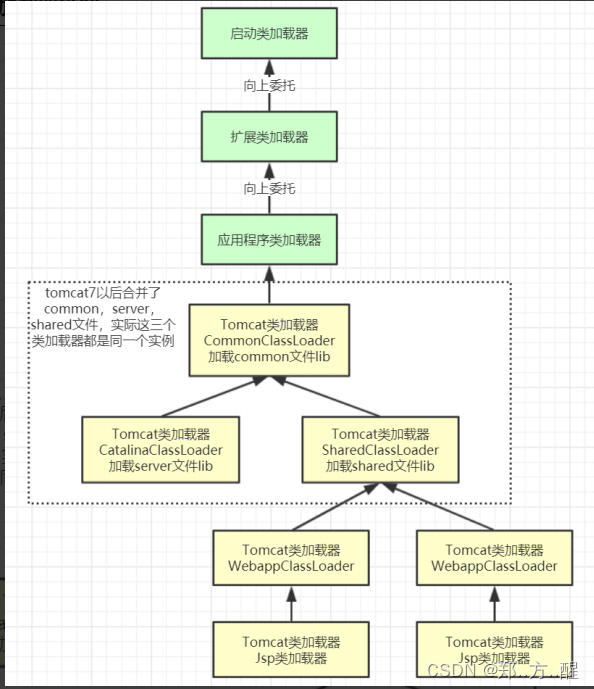
JVM类加载机制详解(JDK源码级别)
提示:从JDK源码级别彻底剖析JVM类加载机制、双亲委派机制、全盘负责委托机制、打破双亲委派机制的程序、Tomcat打破双亲委派机制、tomcat自定义类加载器详解、tomcat的几个主要类加载器、手写tomcat类加载器 文章目录 前言一、loadClass的类加载大概有如下步骤二、j…...

美国年轻人热衷床上“摆烂”,沃尔玛发掘床上用品新商机!
美国年轻人近年来热衷于床上“摆烂”生活方式,这反映了他们对舒适放松的追求和现代生活的压力。沃尔玛作为零售业巨头,敏锐地捕捉到这一市场变化,发现了床上用品的新商机。 美国年轻人忙碌中渴望宁静空间。床成为他们放松、逃离现实压力的理想…...

3168. 候诊室中的最少椅子数
给你一个字符串 s,模拟每秒钟的事件 i: 如果 s[i] E,表示有一位顾客进入候诊室并占用一把椅子。如果 s[i] L,表示有一位顾客离开候诊室,从而释放一把椅子。 返回保证每位进入候诊室的顾客都能有椅子坐的 最少 椅子…...
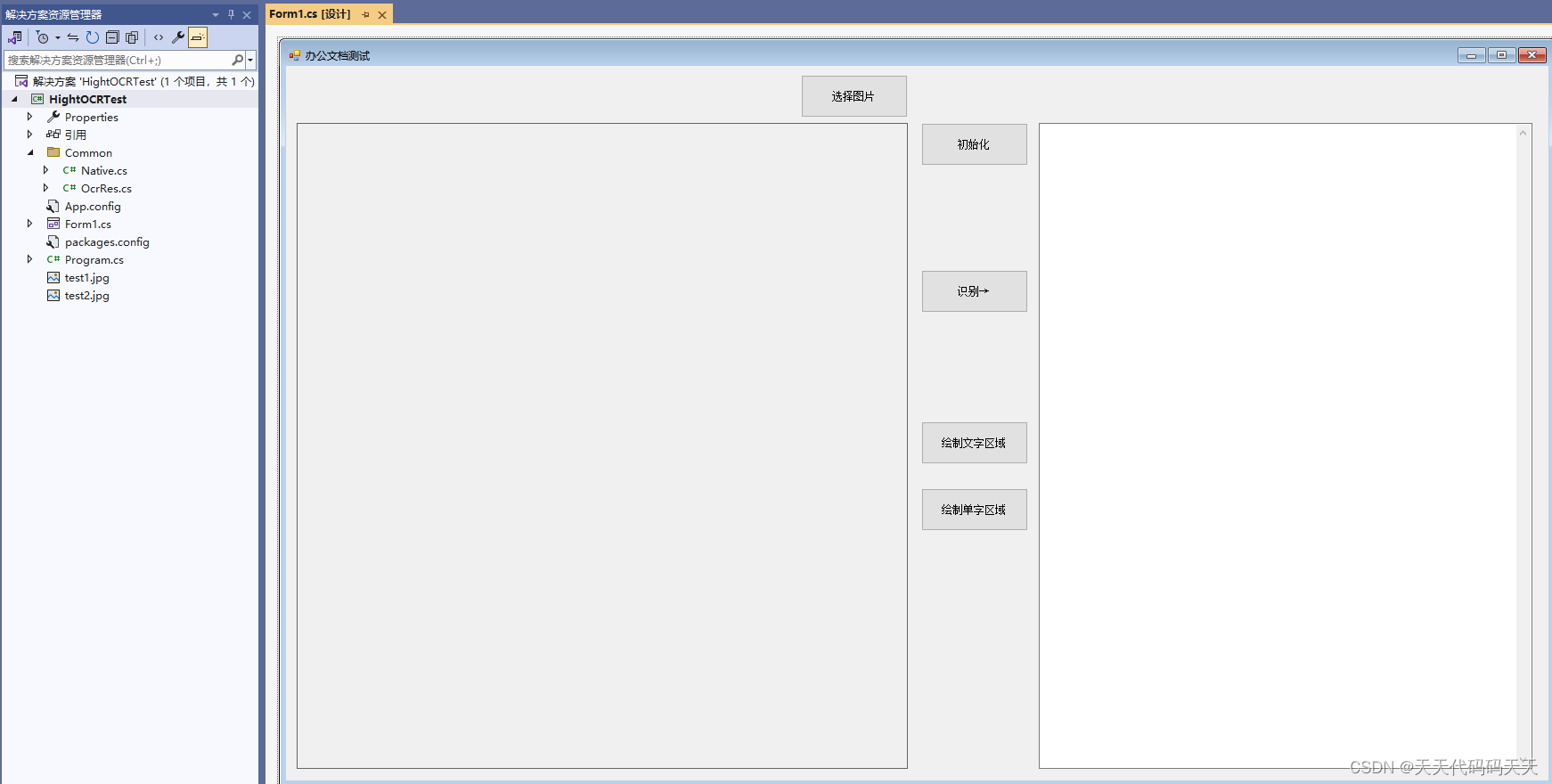
C# PaddleOCR 单字识别效果
C# PaddleOCR 单字识别效果 效果 说明 根据《百度办公文档识别C离线SDKV1.2用户接入文档.pdf》,使用C封装DLL,C#调用。 背景 为使客户、第三方开发者等能够更快速、方便的接入使用百度办公文档识别 SDK、促进百度 OCR产品赋能更多客户,特设…...

pyopengl 立方体 正投影,透视投影
目录 顶点和线的方式 划线的方式实现: 顶点和线的方式 import numpy as np from PyQt5 import QtWidgets from PyQt5.QtCore import Qt from PyQt5.QtWidgets import QApplication, QMainWindow, QPushButton from OpenGL.GL import * from OpenGL.GLU import * import sys…...
人工智能任务5-高级算法工程师需要学习哪些课程与掌握哪些能力
大家好,我是微学AI,今天给大家介绍一下人工智能的任务5-高级算法工程师需要学习哪些课程,需要掌握哪些能力。高级算法工程师需要掌握的算法模型有:人脸检测模型MTCNN,人脸识别方法Siamese network、center loss、softm…...
服务器上创建搭建gitlab
一、下载与安装 在主目录操作~ 1.使用wget下载 wget --no-check-certificate https://mirrors.tuna.tsinghua.edu.cn/gitlab-ce/yum/el7/gitlab-ce-14.0.1-ce.0.el7.x86_64.rpm 可以在开源软件镜像站选择合适的版本,版本不同页面菜单会稍有差异,此次选…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
