当前位置： 首页 > news >正文

【ARM Cache 系列文章 2.1 -- Cache PoP 及 PoDP 介绍】

news 2025/12/25 12:13:02


请阅读【ARM Cache 及 MMU/MPU 系列文章专栏导读】
及【嵌入式开发学习必备专栏】

文章目录

    • PoP 及 PoDP
      • Cache PoDP
      • Cache PoP
      • 应用和影响

PoP 及 PoDP

在这里插入图片描述

Cache PoDP

点对深度持久性（Point of Deep Persistence, PoDP）是内存系统中的一个点，在该点达到的任何写操作即使在系统供电瞬时硬件故障的情况下也是持久的。这意味着，一旦数据写入操作达到 PoDP&

相关文章：

【ARM Cache 系列文章 2.1 -- Cache PoP 及 PoDP 介绍】

请阅读【ARM Cache 及 MMU/MPU 系列文章专栏导读】 及【嵌入式开发学习必备专栏】 文章目录 PoP 及 PoDPCache PoDPCache PoP应用和影响PoP 及 PoDP Cache PoDP 点对深度持久性（Point of Deep Persistence, PoDP）是内存系统中的一个点，在该点达到的任何写操作即使在系统供电…...

编程日记 2024/6/5 23:24:12

一文了解JVM面试篇（上）

Java内存区域 1、如何解释 Java 堆空间及 GC？ 当通过 Java 命令启动 Java 进程的时候，会为它分配内存。内存的一部分用于创建 堆空间，当程序中创建对象的时候，就从对空间中分配内存。GC 是 JVM 内部的一 个进程，回收无效对象的内存用于将来的分配。 2、JVM 的主要组成…...

编程日记 2024/6/5 23:21:09

C#WPF控件Textbox绑定浮点型数据限制小数位方法

本文讲解C#WPF控件Textbox绑定浮点型数据限制小数位方法。 XAML中，使用StringFormat来格式化TextBox的文本 <Window x:Class="WpfApp.MainWindow"xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x="http://schemas.m…...

编程日记 2024/6/5 23:20:08

mysql引入表名称的注意事项

1、遇到问题 mapper中的文件是这样的 解析出来的sql是这样的 sql显示为&#xff1a;select * from ‘tableName’ 2、解决方法 mapper文件种使用${tableName}而不是#{tableName}...

编程日记 2024/6/5 23:19:07

C语言数据结构快速排序的非递归、归并排序、归并排序的非递归等的介绍

文章目录 前言一、快速排序非递归二、归并排序五、归并排序非递归总结 前言 C语言数据结构快速排序的非递归、归并排序、归并排序的非递归等的介绍 一、快速排序非递归 快速排序非递归的定义 快速排序非递归&#xff0c;需要使用栈来实现。将左右下标分别push到栈中。在栈为…...

编程日记 2024/6/5 23:14:01

学生成绩管理系统（大一大作业）

功能 实现添加&#xff0c;排序&#xff0c;修改&#xff0c;保存等功能 库函数 #include<stdio.h> #include<stdlib.h> #include<windows.h> #include<string.h> 头文件 #define functioncreate(major) void major##compare(mana mn){\int i,j,s…...

编程日记 2024/6/5 23:10:58

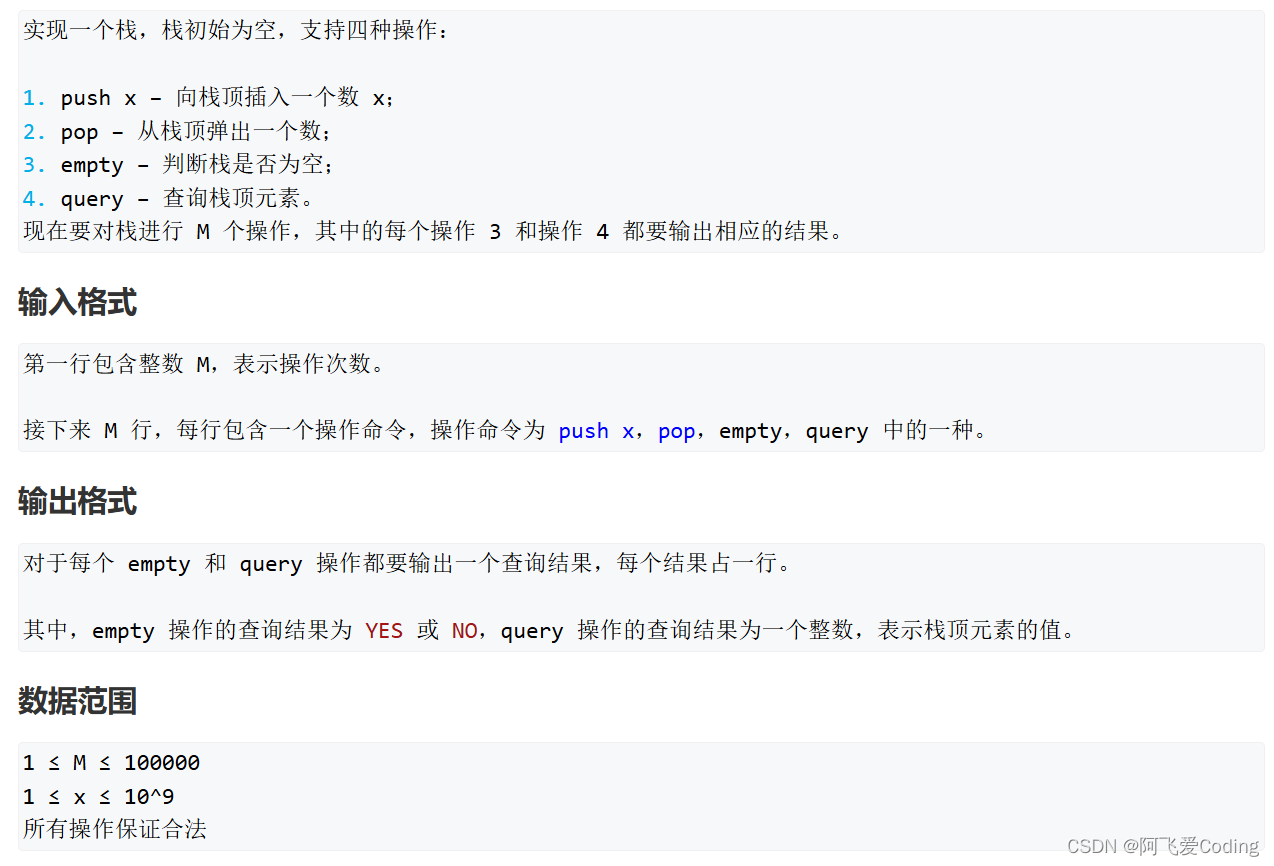
数据结构：模拟栈

数据结构&#xff1a;模拟栈 题目描述参考代码 题目描述 输入样例 10 push 5 query push 6 pop query pop empty push 4 query empty输出样例 5 5 YES 4 NO参考代码 #include <iostream>using namespace std;const int N 1000010;int m, x; int q[N]; string op; int…...

编程日记 2024/6/5 23:09:57

02-2.3.6 顺序表和链表的比较

喜欢《数据结构》部分笔记的小伙伴可以订阅专栏&#xff0c;今后还会不断更新。&#x1f9d1;‍&#x1f4bb; 此外&#xff0c;《程序员必备技能》专栏和《程序员必备工具》专栏&#xff08;该专栏暂未开设&#xff09;日后会逐步更新&#xff0c;感兴趣的小伙伴可以点一下订阅…...

编程日记 2024/6/5 23:08:54

C++ : 模板初阶

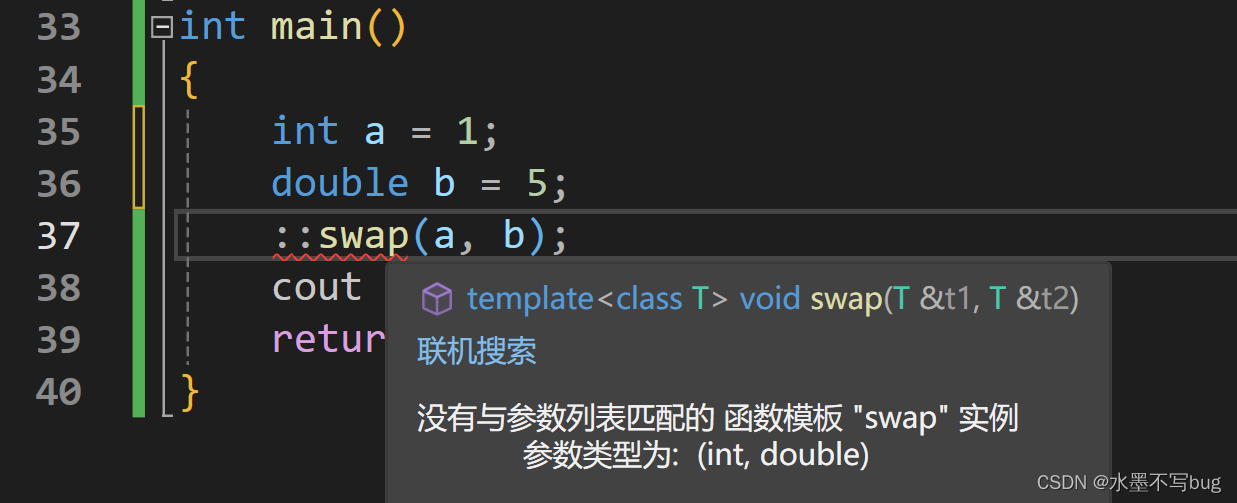
标题&#xff1a;C : 模板初阶 水墨不写bug 正文开始&#xff1a; C语言的问题 &#xff1a; 写不完的swap函数 在学习C语言时&#xff0c;我们有一个经常使用的函数swap函数&#xff0c;它可以将两个对象的值交换。 我们通常这样实现它&#xff1a; void swap(int t1,int t2)…...

编程日记 2024/6/5 23:07:53

FFA-Net：用于单图像去雾的特征融合注意力网络

摘要 论文链接&#xff1a;https://arxiv.org/pdf/1911.07559v2 在这篇论文中&#xff0c;我们提出了一种端到端的特征融合注意力网络&#xff08;FFA-Net&#xff09;来直接恢复无雾图像。FFA-Net架构由三个关键组件组成&#xff1a; 一种新颖的特征注意力&#xff08;FA&…...

编程日记 2024/6/5 23:04:50

网工内推 | 联通公司，云计算售前，AWS认证优先

01 联通数字科技有限公司 &#x1f537;招聘岗位&#xff1a;云计算售前工程师 &#x1f537;职责描述&#xff1a; 1.了解私有云&#xff0c;公有云&#xff0c;混合云等云计算技术知识&#xff0c;了解云计算行业现状及发展趋势。 2.承担区域项目售前工作支持&#xff0c;为…...

编程日记 2024/6/5 23:03:49

[Redis]Zset类型

Zset有序集合相对于字符串、列表、哈希、集合来说会有一些陌生。 它保留了集合不能有重复成员的特点&#xff0c;但与集合不同的是&#xff0c;有序集合中的每个元素都有一个唯一的浮点类型的分数&#xff08;score&#xff09;与之关联&#xff0c;着使得有序集合中的元素是可…...

编程日记 2024/6/5 22:55:37

【云原生】Kubernetes----Ingress对外服务

目录 引言 一、K8S对外方式 &#xff08;一&#xff09;NodePort 1.作用 2.弊端 3.示例 &#xff08;二&#xff09;externalIPs 1.作用 2.弊端 3.示例 &#xff08;三&#xff09;LoadBalancer 1.作用 2.弊端 &#xff08;四&#xff09;Ingress 二、Ingress的…...

编程日记 2024/6/5 22:54:36

项目管理之maven svn

管理jar包之间依赖关系 编译、打包、清理、测试等一系列构建工具 一、Maven的标志 1、每一个maven工程都有一个pom.xml maven项目坐标 <groupId>com.aaa</groupId>//项目路径 <artifactId>web</artifactId>项目名称 <version>0.0.1-SNAPS…...

编程日记 2024/6/5 22:53:35

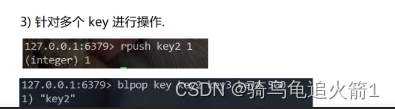
Redis篇 list类型在Redis中的命令操作

list在redis基本的命令 一.基本命令1.lpush和range2.lpushx rpushx3.lpop rpop4.lindex linsert llen5.lrem6.ltrim lset7.blpop brpop 一.基本命令 list在redis中相当于数组或者顺序表. 1.lpush和range 2.lpushx rpushx 3.lpop rpop 4.lindex linsert llen 如果要插入的列表中…...

编程日记 2024/6/5 22:52:34

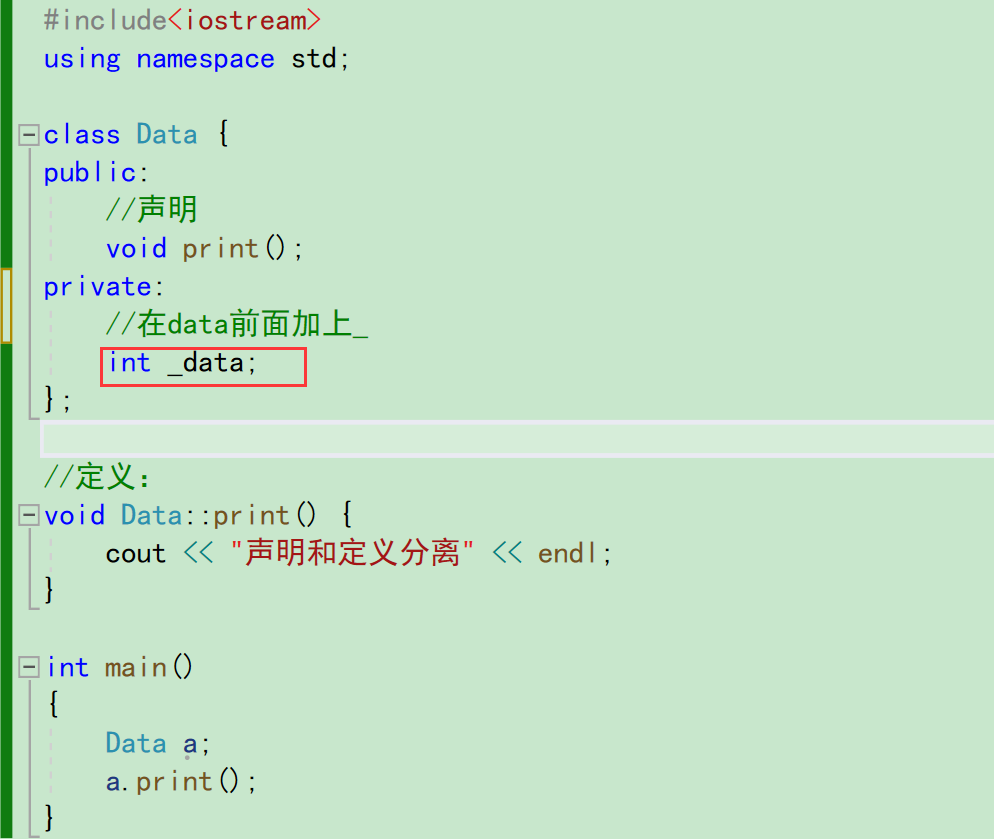
【C++课程学习】：类和对象（上）（类的基础详细讲解）

&#x1f381;个人主页&#xff1a;我们的五年 &#x1f50d;系列专栏&#xff1a;C课程学习 &#x1f389;欢迎大家点赞&#x1f44d;评论&#x1f4dd;收藏⭐文章 目录 &#x1f35f;1.1类的引出&#xff1a; &#x1f35f;1.2类的结构&#xff1a; &#x1f35f;1.3类的…...

编程日记 2024/6/5 22:51:33

HTML 转义字符（escape characters）及其对应的符号（symbols）

以下是常见的 HTML 转义字符及其对应的符号&#xff0c;这些可以用于在 HTML 或 JSX 中避免解析错误和特殊字符的冲突&#xff1a; 空格 ( ): 或 引号: 单引号&#xff08;&#xff09;&#xff1a;&apos;、&lsquo;、、&rsquo;双引号&#xff08;"&#x…...

编程日记 2024/6/5 22:45:27

CPASSOC代码详解

加载环境 library("MASS") require(MASS) # Modern Applied Statistics with S&#xff0c;"S"指的是S语言&#xff0c;由贝尔实验室的约翰钱伯斯&#xff08;John Chambers&#xff09;等人开发。S语言是R语言的前身&#xff0c;许多R语言的语法和功能都…...

编程日记 2024/6/5 22:42:24

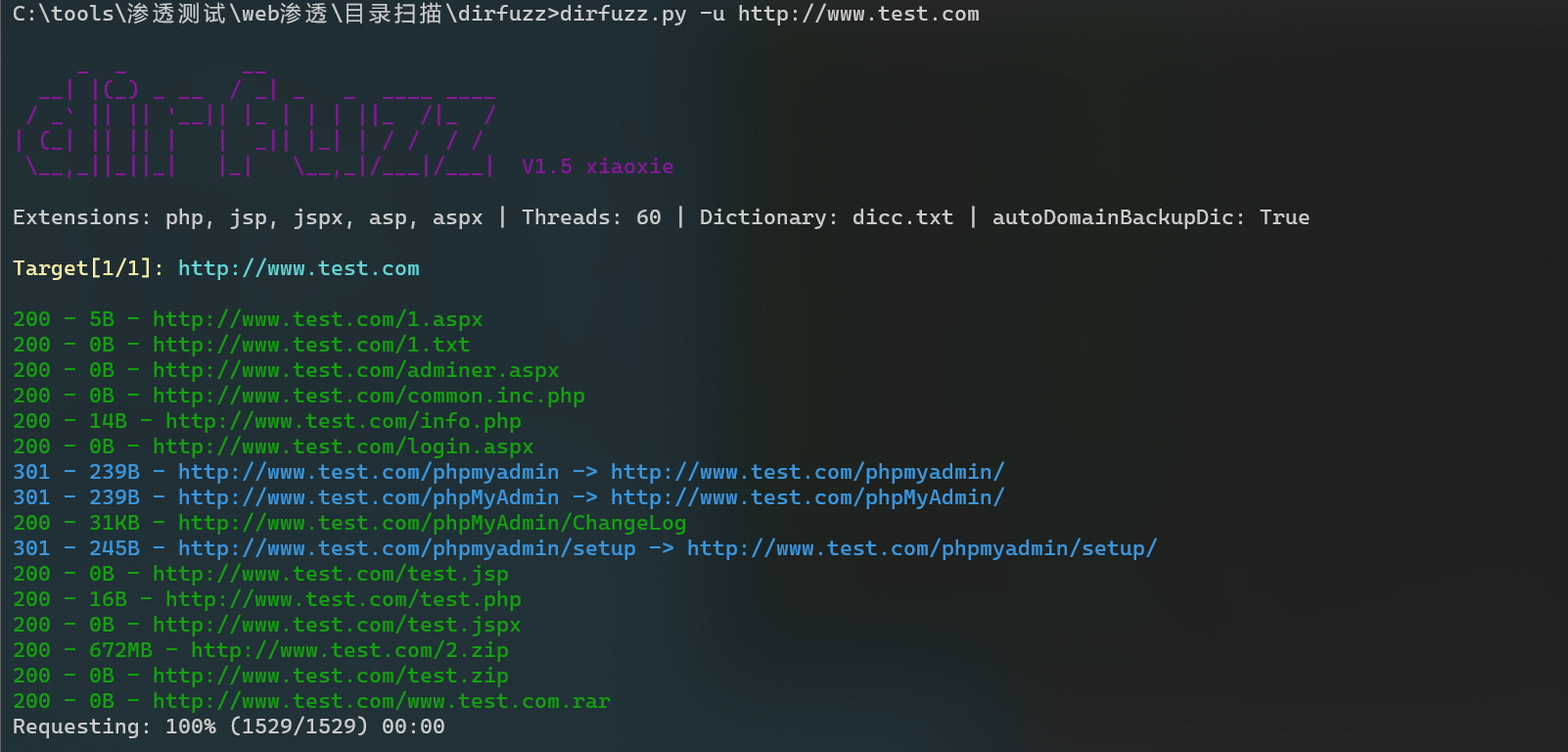
dirfuzz-web敏感目录文件扫描工具

dirfuzz介绍 dirfuzz是一款基于Python3的敏感目录文件扫描工具&#xff0c;借鉴了dirsearch的思路&#xff0c;扬长避短。在根据自身实战经验的基础上而编写的一款工具&#xff0c;经过断断续续几个月的测试、修改和完善。 项目地址&#xff1a;https://github.com/ssrc-c/di…...

编程日记 2024/6/5 22:41:23

计算机发展史 | 从起源到现代技术的演进

computer | Evolution from origins to modern technology 今天没有参考资料哈哈 PPT&#xff1a;&#xff08;评论区&#xff1f;&#xff09; 早期计算工具 算盘 -算盘是一种手动操作的计算辅助工具&#xff0c;起源于中国&#xff0c;迄今已有2600多年的历史&#xff0c;是…...

编程日记 2024/6/5 22:40:22

大数据学习栈记——Neo4j的安装与使用

本文介绍图数据库Neofj的安装与使用&#xff0c;操作系统&#xff1a;Ubuntu24.04&#xff0c;Neofj版本&#xff1a;2025.04.0。 Apt安装 Neofj可以进行官网安装&#xff1a;Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

编程新知 2025/12/22 11:05:42

ubuntu搭建nfs服务centos挂载访问

在Ubuntu上设置NFS服务器 在Ubuntu上&#xff0c;你可以使用apt包管理器来安装NFS服务器。打开终端并运行&#xff1a; sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享&#xff0c;例如/shared&#xff1a; sudo mkdir /shared sud…...

编程新知 2025/8/27 13:05:41

PHP和Node.js哪个更爽?

先说结论&#xff0c;rust完胜。 php&#xff1a;laravel&#xff0c;swoole&#xff0c;webman&#xff0c;最开始在苏宁的时候写了几年php&#xff0c;当时觉得php真的是世界上最好的语言&#xff0c;因为当初活在舒适圈里&#xff0c;不愿意跳出来&#xff0c;就好比当初活在…...

编程新知 2025/9/14 7:59:52

【第二十一章 SDIO接口(SDIO)】

第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

编程新知 2025/12/24 18:48:44

高防服务器能够抵御哪些网络攻击呢？

高防服务器作为一种有着高度防御能力的服务器&#xff0c;可以帮助网站应对分布式拒绝服务攻击&#xff0c;有效识别和清理一些恶意的网络流量&#xff0c;为用户提供安全且稳定的网络环境&#xff0c;那么&#xff0c;高防服务器一般都可以抵御哪些网络攻击呢&#xff1f;下面…...

编程新知 2025/9/3 19:14:38

【论文阅读28】-CNN-BiLSTM-Attention-（2024）

本文把滑坡位移序列拆开、筛优质因子&#xff0c;再用 CNN-BiLSTM-Attention 来动态预测每个子序列&#xff0c;最后重构出总位移&#xff0c;预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵&#xff08;S…...

编程新知 2025/12/14 18:18:37

【Oracle】分区表

个人主页&#xff1a;Guiat 归属专栏&#xff1a;Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

编程新知 2025/12/24 9:55:32

uniapp 字符包含的相关方法

在uniapp中&#xff0c;如果你想检查一个字符串是否包含另一个子字符串&#xff0c;你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的&#xff0c;但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

编程新知 2025/9/28 19:00:18

关于uniapp展示PDF的解决方案

在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项&#xff1a; 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库&#xff1a; npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

编程新知 2025/9/18 20:16:52

解析奥地利 XARION激光超声检测系统：无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用

在工业制造领域&#xff0c;无损检测&#xff08;NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统&#xff0c;以非接触式光学麦克风技术为核心&#xff0c;打破传统检测瓶颈&#xff0c;为半导体、航空航天、汽车制造等行业提供了高灵敏…...

编程新知 2025/12/24 20:37:35