【LeetCode】每日一题 2024_6_4 将元素分配到两个数组中 II(二分、离散化、树状数组)
文章目录
- LeetCode?启动!!!
- 题目:将元素分配到两个数组中 II
- 题目描述
- 代码与解题思路
- 每天进步一点点
LeetCode?启动!!!

又有段时间没写每日一题的分享了,原本今天是打算早上发完晨起计划之后发的,但是今天太忙了,忙着忙着一直没时间把文章写完,拖着拖着就拖到晚上了
只能在晚上离散数学的课上悄摸摸写完发了
题目:将元素分配到两个数组中 II
题目链接:将元素分配到两个数组中 II
题目描述

代码与解题思路
// 树状数组
type fenwick []int// 维护 [1, i] 的元素个数
func (f fenwick) add(i int) {for ; i < len(f); i += i & -i {f[i]++}
}// 获取 [1, i] 的元素个数和
func (f fenwick) pre(i int) (res int) {for ; i > 0; i &= i - 1 {res += f[i]}return res
}func resultArray(nums []int) []int {// 排序去重 -> 离散化sorted := slices.Clone(nums)slices.Sort(sorted)sorted = slices.Compact(sorted)m := len(sorted)a, b := []int{nums[0]}, []int{nums[1]}// 维护树状数组t1, t2 := make(fenwick, m+1), make(fenwick, m+1)for i, v := range sorted {if v == nums[0] {t1.add(i+1)} if v == nums[1] {t2.add(i+1)}}for _, x := range nums[2:] {// 二分查找离散化数组的下标位置l, r := 0, len(sorted)for l < r {mid := (l+r)>>1if sorted[mid] < x {l = mid+1} else {r = mid}}v := l+1// greaterCount: 用数组所有元素 - 小于等于 val 元素的数量 = 大于 val 元素的数量gc1 := len(a) - t1.pre(v)gc2 := len(b) - t2.pre(v)if gc1 > gc2 || gc1 == gc2 && len(a) <= len(b) {a = append(a, x)t1.add(v)} else {b = append(b, x)t2.add(v)}}return append(a, b...)
}
代码的核心思路比较短,题目比较好理解(看着像是一个简单的模拟题)但是他给到的数据范围是 10^5,也就是他没法用暴力的算法去做
根据题目需要维护大于某个数的元素个数的要求,以及 10^9 次方的数字大小,我们可以用离散化 + 维护树状数组解决
两个问题
1)如何离散化?
sorted := slices.Clone(nums)
slices.Sort(sorted)
sorted = slices.Compact(sorted)
排序去重好的 sorted 数组,假设是 [ 7, 12, 23, 40 ],我们在 nums 数组找到 23 这个元素的时候,就能根据这个元素在 sorted 数组中的位置,求的有 2 个数比他小,1 个数比他大
这就是离散化的意义
2)树状数组?
// 树状数组
type fenwick []int// 维护 [1, i] 的元素个数
func (f fenwick) add(i int) {for ; i < len(f); i += i & -i {f[i]++}
}// 获取 [1, i] 的元素个数和
func (f fenwick) pre(i int) (res int) {for ; i > 0; i &= i - 1 {res += f[i]}return res
}
关于上述代码的解释:(对于树状数组的简单解释)
为什么用树状数组?因为树状数组能够 logN 获取一个区间的前缀和,并能够 logN 的复杂度修改区间的值。
树状数组中,通过不断加上 lowbit 可以获得每个关键区间,让 [1, i] 区间增加或减少一个值(add 操作)
而通过不断减去 lowbit 可以获得区间和 [1, i](pre 操作)
求 lowbit 的方法:i & -i
减去 lowbit 的方法:i &= i-1
什么是 lowbit?
=> 10010 中,10 就是 lowbit
每天进步一点点
可以和我刷一辈子的每日一题吗?
一题一题,积累起来就是一辈子。
相关文章:

【LeetCode】每日一题 2024_6_4 将元素分配到两个数组中 II(二分、离散化、树状数组)
文章目录 LeetCode?启动!!!题目:将元素分配到两个数组中 II题目描述代码与解题思路 每天进步一点点 LeetCode?启动!!! 又有段时间没写每日一题的分享了,原本今…...
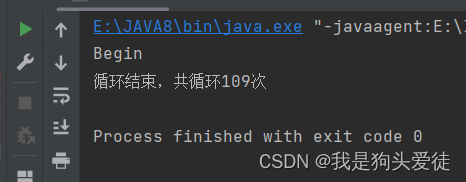
JAVA小案例-break练习,随机数,到88停止
JAVA小案例-break练习,随机数,到88停止 代码如下: public class Break {/*** break练习,随机数,到88停止* param args*/public static void main(String[] args) {int count0;//计数器System.out.println("Begi…...
C++第三方库【httplib】断点续传
什么是断点续传 上图是我们平时在浏览器下载文件的场景,下载的本质是数据的传输。当出现网络异常,浏览器异常,或者文件源的服务器异常,下载都可能会终止。而当异常解除后,重新下载文件,我们希望从上一次下载…...
[SaaS] AI+数据,tiktok选品,找达人,看广告数据
TK观察专访丨前阿里“鲁班”创始人用AIGC赋能TikTok获千万融资用AI数据做TikTokhttps://mp.weixin.qq.com/s/xp5UM3ROo48DK4jS9UBMuQ主要还是爬虫做数据的。 商家做内容:1.找达人拍内容,2.商家自己做原生自制内容,3.广告内容。 短视频&…...
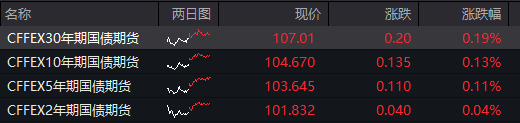
A股冲高回落,金属、地产板块领跌,新股N汇成真首日暴涨753%
行情概述 AH股有色金属、教育及地产板块领跌,军工航天及半导体板块逆势走强;锂电池、创新药概念股也走强。创业板新股N汇成真首日暴涨753%,触发二次临停。 周三A股冲高回落,上证指数收跌0.83%,深成指跌0.8%ÿ…...
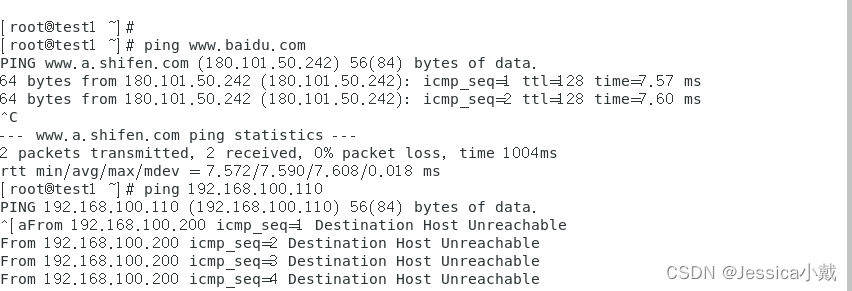
dns域名解析服务和bond网卡
目录 dns域名解析服务 一、DNS 1、定义 2、以www.baidu.com为例 3、域名体系结构 4、DNS解析使用的协议和端口 5、dns域名解析的过程 6、dns解析的优先级 二、如何实现域名解析 1、域名解析 2、bind配置文件位置 (一)正向解析 (…...

视频生成框架EasyAnimate正式开源!
近期,Sora模型的热度持续上涨,社区中涌现了一些类Sora的开源项目,这些项目均基于Diffusion Transformer结构,使用Transformer结构取代了UNet作为扩散模型的基线,旨在生成更长、更高分辨率、且效果更好的视频。EasyAnim…...
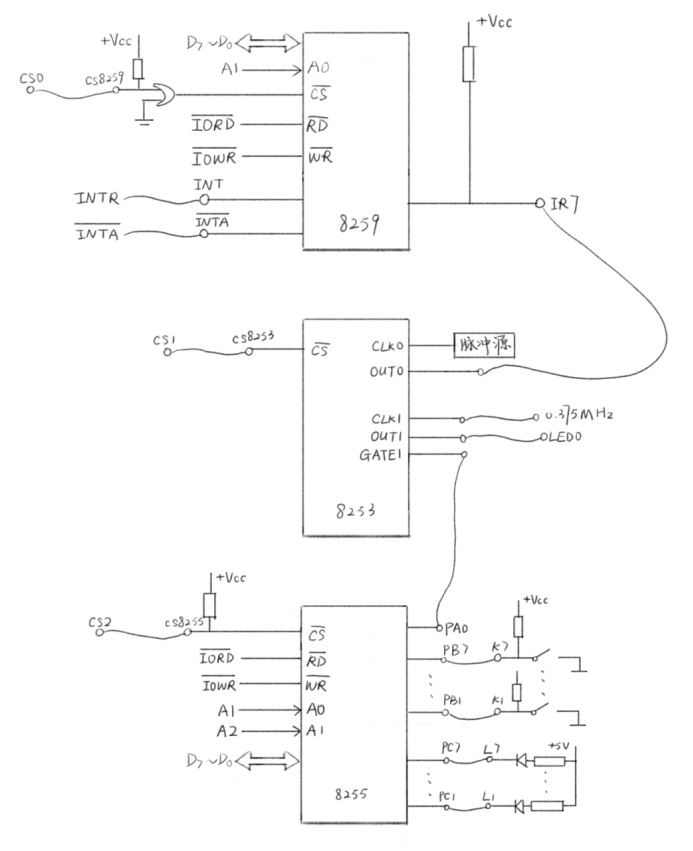
【微机原理与汇编语言】并行接口8255实验
一、实验目的 掌握可编程并行接口芯片8255的工作原理及初始化方法掌握8255在实际应用中的硬件连接及编程应用 二、实验要求 根据实验室现有条件,针对实验任务,设计实验方案并进行实现。 三、实验内容 启动0#计数器,每计5个数(…...

Oracle表分区的基本使用
什么是表空间 是一个或多个数据文件的集合,所有的数据对象都存放在指定的表空间中,但主要存放的是表,所以称为表空间 什么是表分区 表分区就是把一张大数据的表,根据分区策略进行分区,分区设置完成之后,…...
6月5号作业
设计一个Per类,类中包含私有成员:姓名、年龄、指针成员身高、体重,再设计一个Stu类,类中包含私有成员:成绩、Per类对象p1,设计这两个类的构造函数、析构函数 #include <iostream>using namespace std; class Slu { priv…...

中继器、集线器、网桥、交换机、路由器和网关
目录 前言一、中继器、集线器1.1 中继器1.2 集线器 二、网桥、交换机2.1 网桥2.1.1 认识网桥2.1.2 网桥的工作原理2.1.3 生成树网桥 2.2 交换机2.2.1 交换机的特征2.2.2 交换机的交换模式2.2.3 交换机的功能 三、路由器、网关3.1 路由器的介绍3.2 路由器的工作过程3.2.1 前置知…...

揭秘相似矩阵:机器学习算法中的隐形“纽带”
在机器学习领域,数据的处理和分析至关重要。如何有效地从复杂的数据集中提取有价值的信息,是每一个机器学习研究者都在努力探索的问题。相似矩阵,作为衡量数据之间相似性的数学工具,在机器学习算法中扮演着不可或缺的角色。 相似矩…...
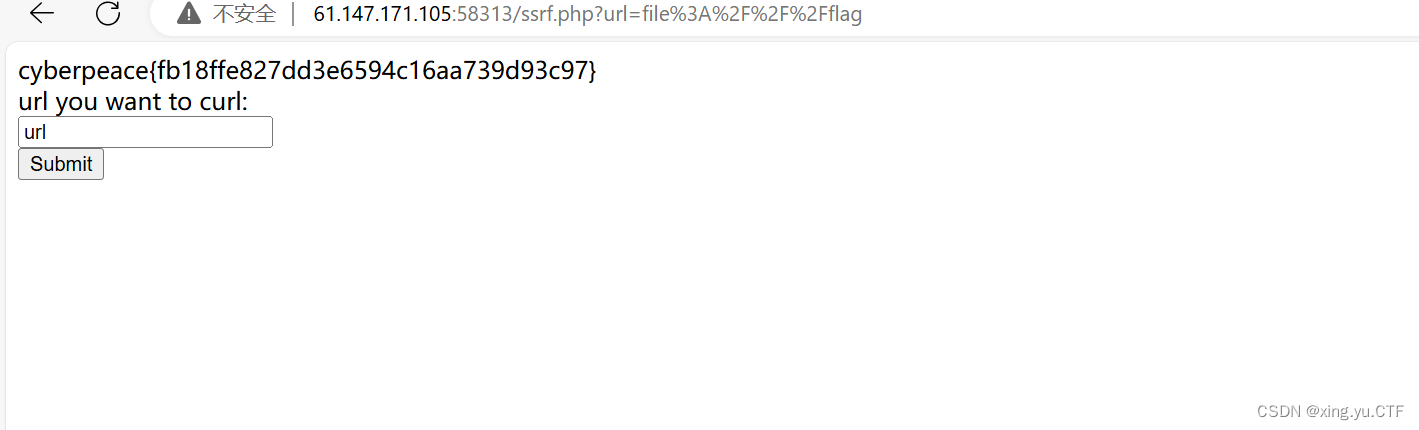
攻防世界—webbaby详解
1.ssrf注入漏洞 ssrf(服务端请求伪造)是一种安全漏洞,攻击者通过该漏洞向受害服务器发出伪造的请求,从而访问并获取服务器上的资源,常见的ssrf攻击场景包括访问内部网络的服务,执行本地文件系统命令&#…...
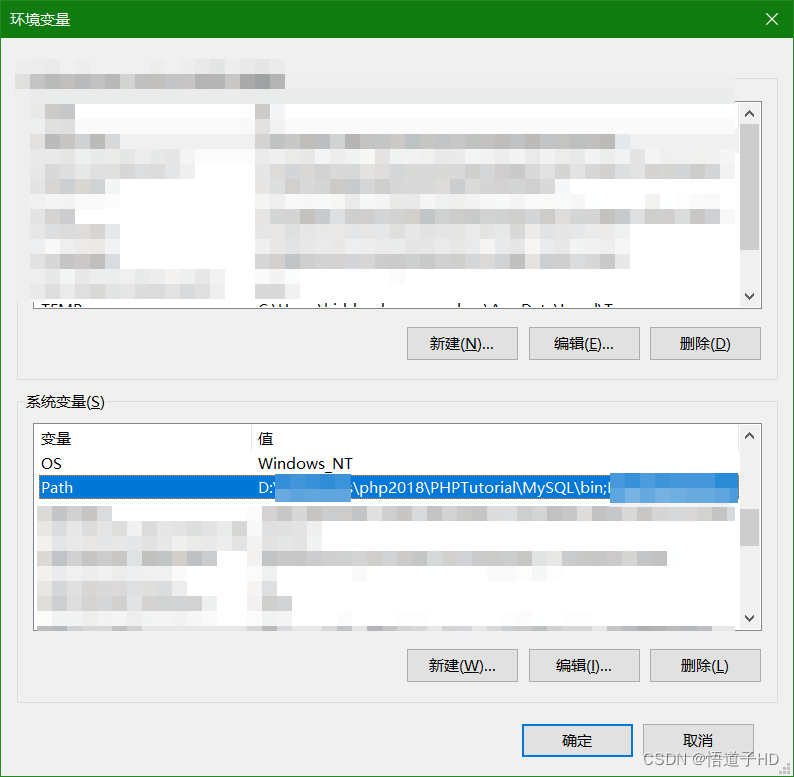
MySQL中:cmd下输入命令mysql -uroot -p 连接数据库错误
目录 问题cmd下输入命令mysql -uroot -p错误 待续、更新中 问题 cmd下输入命令mysql -uroot -p错误 解决 配置环境变量:高级系统设置——环境变量——系统变量——path编辑——新建——MySQL.exe文件路径(如下图所示) phpstudy2018软件下&am…...

【开发利器】使用OpenCV算子工作流高效开发
学习《人工智能应用软件开发》,学会所有OpenCV技能就这么简单! 做真正的OpenCV开发者,从入门到入职,一步到位! OpenCV实验大师Python SDK 基于OpenCV实验大师v1.02版本提供的Python SDK 实现工作流导出与第三方应用集…...
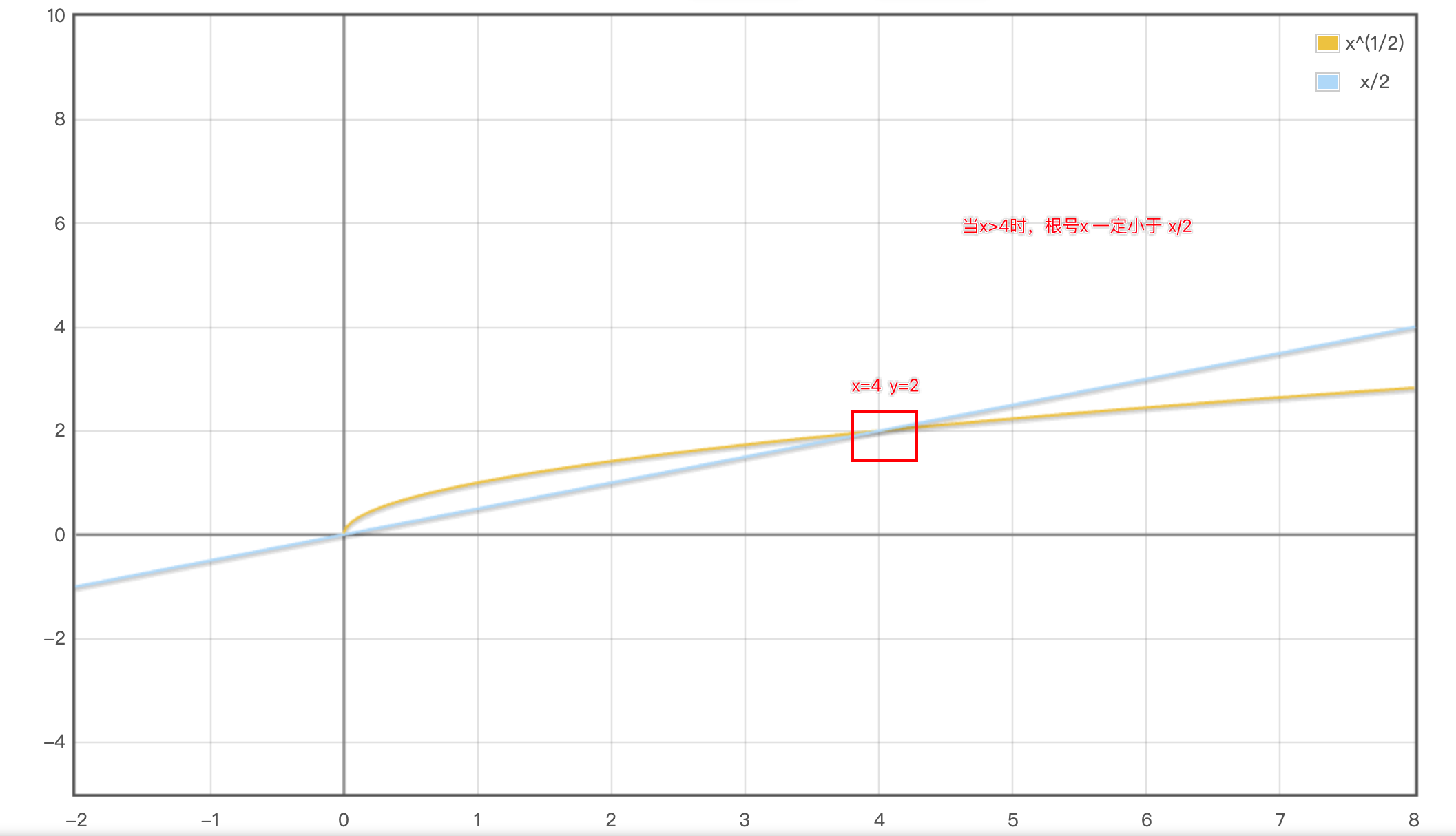
基础数学-求平方根(easy)
一、问题描述 二、实现思路 1.题目不能直接调用Math.sqrt(x) 2.这个题目可以使用二分法来缩小返回值范围 所以我们在left<right时 使 mid (leftright)/21 当mid*mid>x时,说明right范围过大,rightright-1 当mid*mid<x时,说明left范…...

c语言项目-贪吃蛇项目2-游戏的设计与分析
文章目录 前言游戏的设计与分析地图:这里简述一下c语言的国际化特性相关的知识<locale.h> 本地化头文件类项setlocale函数 上面我们讲到需要打印★,●,□三个宽字符找到这三个字符打印的方式有两种: 控制台屏幕的长宽特性&a…...

力扣2831.找出最长等值子数组
力扣2831.找出最长等值子数组 思路:用二维数组存每个数字的出现下标 遍历所有数字求结果当前子数组大小:pos[i] - pos[j] 1;当前相同数个数:i - j 1;需要删去的数的个数:pos[i] - pos[j] - i j; class Solution {public:int…...

17K star,一款开源免费的手机电脑无缝同屏软件
导读:白茶清欢无别事,我在等风也等你。 作为程序员,在我们的工作中经常需要把手机投票到电脑进行调试工作,选择一款功能强大的投屏软件是一件很必要的事情。今天给大家介绍一款开源且免费的投屏软件,极限投屏ÿ…...

正则表达式二
修饰符 i:将匹配设置为不区分大小写,即A和a没有区别 var str"Google Runoob taobao runoob"; var n1str.match(/runoob/g); //runoob var n2str.match(/runoob/gi); //Runoob,runoobg:重找所有匹配项࿰…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
