代码随想录算法训练营第四十四天 | 01背包问题理论基础、01背包问题滚动数组、416. 分割等和子集
背包问题其实有很多种,01背包是最基础也是最经典的,软工计科学生一定要掌握的。

01背包问题
代码随想录
视频讲解:带你学透0-1背包问题!| 关于背包问题,你不清楚的地方,这里都讲了!| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili
思路
直接上动态规划五部曲
1、dp数组及其下标的含义
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
2.确定递推公式
再回顾一下dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
那么可以有两个方向推出来dp[i][j],
- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
3.初始化
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。
再看其他情况。
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
4.确定遍历顺序
在如下图中,可以看出,有两个遍历的维度:物品与背包重量
那么问题来了,先遍历 物品还是先遍历背包重量呢?
其实都可以!! 但是先遍历物品更好理解。
5.举例验证,直接看链接里的吧。
代码
def test_2_wei_bag_problem1():weight = [1, 3, 4]value = [15, 20, 30]bagweight = 4# 二维数组dp = [[0] * (bagweight + 1) for _ in range(len(weight))]# 初始化for j in range(weight[0], bagweight + 1):dp[0][j] = value[0]# weight数组的大小就是物品个数for i in range(1, len(weight)): # 遍历物品for j in range(bagweight + 1): # 遍历背包容量if j < weight[i]:dp[i][j] = dp[i - 1][j]else:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])print(dp[len(weight) - 1][bagweight])test_2_wei_bag_problem1()
01背包滚动数组
代码随想录
视频讲解:带你学透01背包问题(滚动数组篇) | 从此对背包问题不再迷茫!_哔哩哔哩_bilibili
看链接吧,老是复制粘贴累了。
416.分割等和子集
本题是 01背包的应用类题目代码随想录
视频讲解:动态规划之背包问题,这个包能装满吗?| LeetCode:416.分割等和子集_哔哩哔哩_bilibili
思路
就是01背包的应用,背包的大小是总和的一半,遍历每一个物品,看看遍历到最后能不能装满这个背包。
代码(二维版本在链接里)
class Solution:def canPartition(self, nums: List[int]) -> bool:if sum(nums) % 2 != 0:return Falsetarget = sum(nums) // 2dp = [0] * (target + 1)for num in nums:for j in range(target, num-1, -1):dp[j] = max(dp[j], dp[j-num] + num)return dp[-1] == target相关文章:

代码随想录算法训练营第四十四天 | 01背包问题理论基础、01背包问题滚动数组、416. 分割等和子集
背包问题其实有很多种,01背包是最基础也是最经典的,软工计科学生一定要掌握的。 01背包问题 代码随想录 视频讲解:带你学透0-1背包问题!| 关于背包问题,你不清楚的地方,这里都讲了!| 动态规划经…...

【PingPong_注册安全分析报告】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞 …...
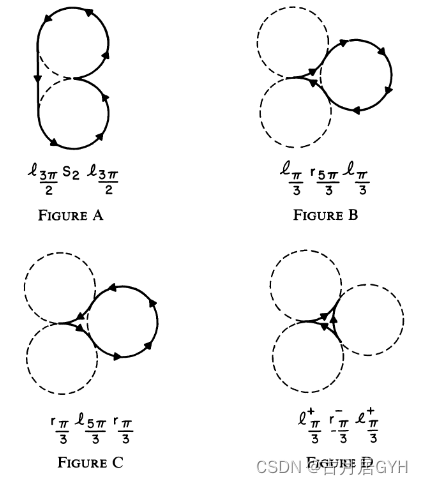
车辆路径规划之Dubins曲线与RS曲线简述
描述 Dubins和RS曲线都是路径规划的经典算法,其中车辆运动学利用RS曲线居多,因此简单介绍Dubins并引出RS曲线。 花了点时间看了二者的论文,并阅读了一个开源的代码。 Dubins曲线 Dubins曲线是在满足曲率约束和规定的始端和末端的切线&#…...

PostgreSQL 和Oracle锁机制对比
PostgreSQL 和Oracle锁机制对比 PostgreSQL 和 Oracle 都是业界广泛使用的关系型数据库管理系统,它们在锁机制方面都有独到的设计来控制并发访问,确保数据的一致性和完整性。下面我们详细比较一下这两个数据库系统的锁机制。 1. 锁类型 PostgreSQL P…...

6月05日,每日信息差
第一、特斯拉在碳博会上展示了其全品类的可持续能源解决方案,包括首次在国内展出的超大型电化学商用储能系统 Megapack 和家庭储能系统 Powerwall。此外,特斯拉还展示了电动汽车三电系统的解构和电池回收技术产品 第二、2024 年第一季度,全球…...

MongoDB~俩大特点管道聚合和数据压缩(snappy)
场景 在MySQL中,通常会涉及多个表的一些操作,MongoDB也类似,有时需要将多个文档甚至是多个集合汇总到一起计算分析(比如求和、取最大值)并返回计算后的结果,这个过程被称为 聚合操作 。 根据官方文档介绍&…...

HTML+CSS+JS 动态登录表单
效果演示 实现了一个登录表单的背景动画效果,包括一个渐变背景、一个输入框和一个登录按钮。背景动画由多个不同大小和颜色的正方形组成,它们在页面上以不同的速度和方向移动。当用户成功登录后,标题会向上移动,表单会消失。 Code <!DOCTYPE html> <html lang=&q…...

统一返回响应
前言 我们为什么要设置统一返回响应 提高代码的可维护性:通过统一返回请求的格式,可以使代码更加清晰和易于维护,减少重复的代码,提高代码质量。 便于调试和测试:统一的返回格式使得在调试和测试时更为简单ÿ…...
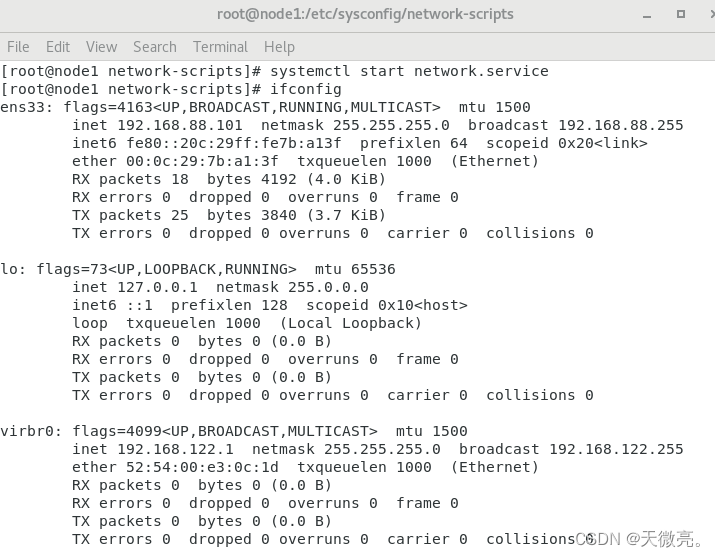
大数据学习问题记录
问题记录 node1突然无法连接finalshell node1突然无法连接finalshell 今天我打开虚拟机和finalshell的时候,发现我的node1连接不上finalshell,但是node2、node3依旧可以链接,我在网上找了很多方法,但是是关于全部虚拟机连接不上finalshell&a…...
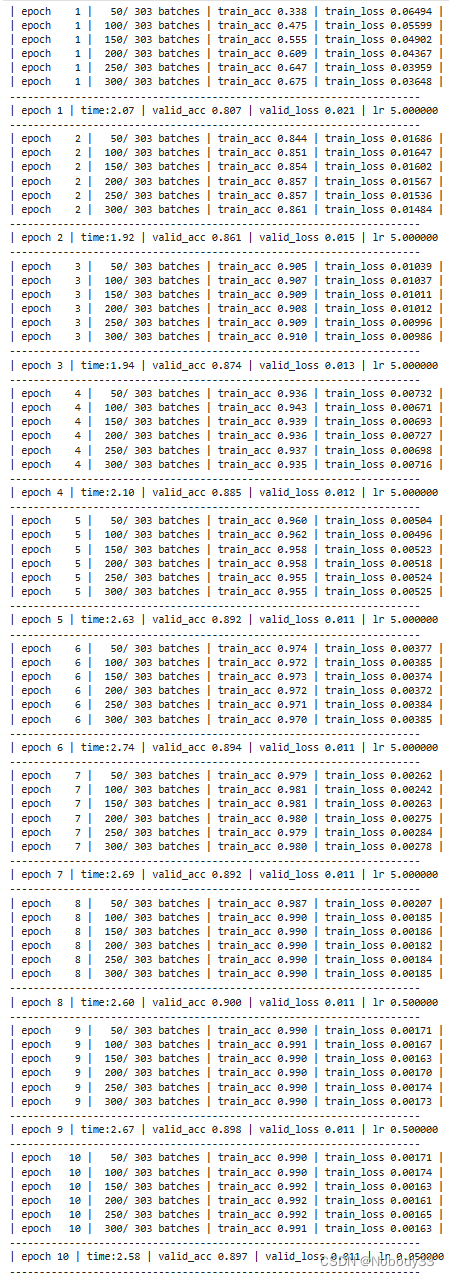
第N4周:中文文本分类
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 一、预备知识 中文文本分类和英文文本分类都是文本分类,为什么要单独拎出来个中文文本分类呢? 在自然语言处理(NLP&#x…...
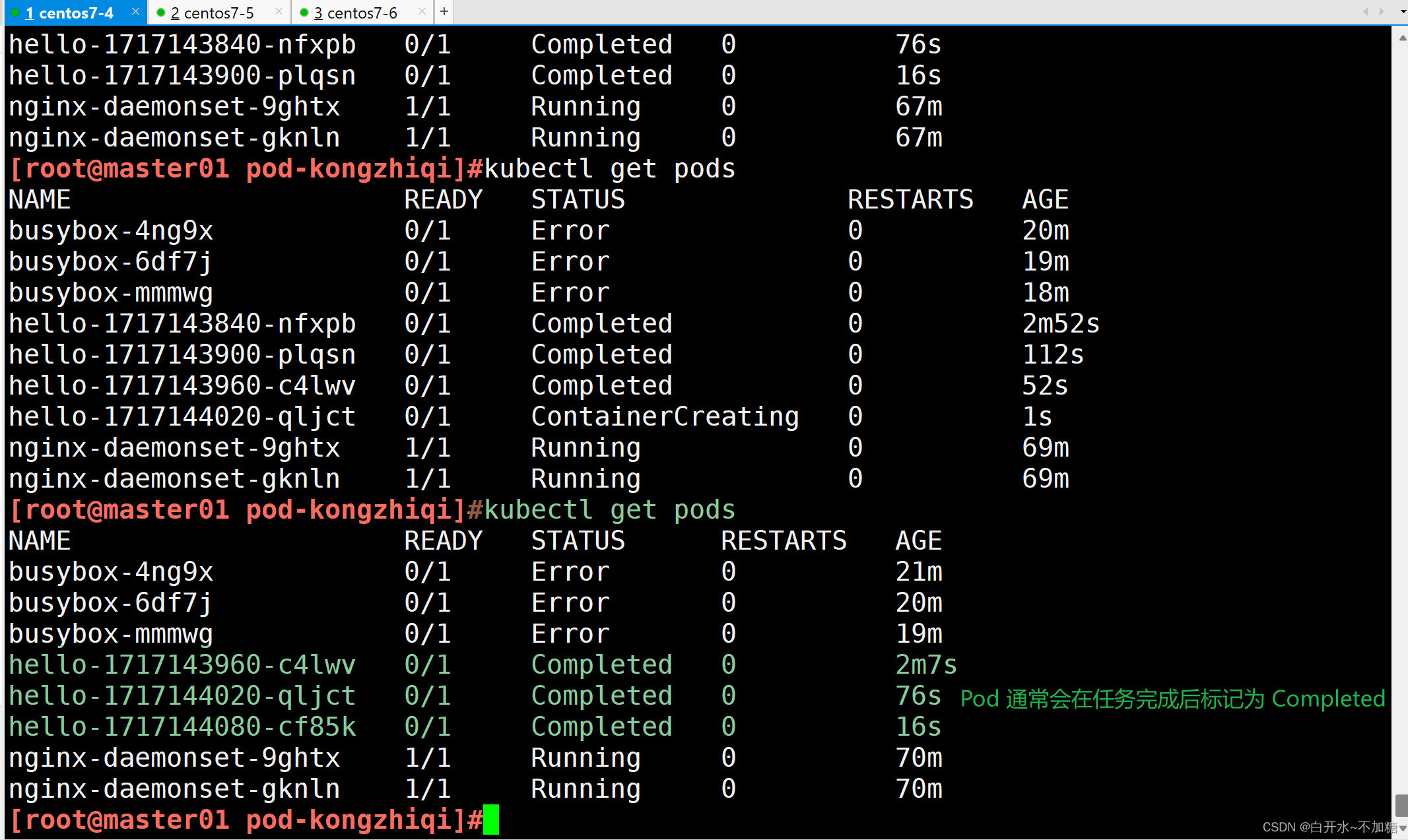
【kubernetes】探索k8s集群的pod控制器详解(Deployment、StatefulSet、DaemonSet、Job、CronJob)
目录 一、Pod控制器及其功用 二、pod控制器有多种类型 2.1ReplicaSet 2.1.1ReplicaSet主要三个组件组成 2.2Deployment 2.3DaemonSet 2.4StatefulSet 2.5Job 2.6Cronjob 三、Pod与控制器之间的关系 3.1Deployment 3.2SatefulSet 3.2.1StatefulSet三个组件 3.2.2为…...

直接插入排序
#include <stdio.h>void insert_sort(int arr[], int n) {int i;int j;int tmp;for (i 1; i < n; i){tmp arr[i];j i - 1;// 将要插入的元素与数组中的元素比较(从后向前比) while (j > 0 && arr[j] > tmp){arr[j 1] arr[…...

esp32s3 nvs 存储过程中使用malloc和free函数的一点困惑
我的项目中,大量使用了malloc()和free()函数,在使用nvs存储之前没有出现问题。 esp32厂家nvs的blob存储的例程中,有使用malloc()和free(),我参照例程写了自己的blob存储函数f,一开始是可以正常使用的,后来…...

除visio以外的几款好用流程图绘制工具
流程图绘制软件在嵌入式软件开发中扮演着重要的角色,它们能够帮助用户清晰、直观地展示工作流程。以下是几款流行的流程图绘制软件及其特点的详细报告: 思维导图MindMaster MindMaster作为一款专业的思维导图软件,不仅具备强大的思维导图制作…...

CentOS 7 64位 常用命令
一、系统管理命令 systemctl start firewalld.service:启动防火墙服务 systemctl stop firewalld.service:停止防火墙服务 systemctl enable firewalld.service:设置防火墙服务开机自启 systemctl disable firewalld.service:禁止…...

ChatGPT-4o抢先体验
速度很快,结果很智能,支持多模态输入输出,感兴趣联系作者。 windows/linux/mac 客户端下载参考:https://github.com/lencx/Noi...

STM32实验之USART串口发送+接受数据(二进制/HEX/文本)
涉及三个实验: 1.USART串口发送和接收数据 我们使用的是将串口封装成为一个Serial.c模块.其中包含了 void Serial_Init(void);//串口初始化 void Serial_SendByte(uint8_t Byte);//串口发送一个字节 void Serial_SendArray(uint8_t *Array,uint16_t Length);//…...

网关(Gateway)- 内置过滤器工厂
官方文档:Spring Cloud Gateway 内置过滤器工厂 AddRequestHeaderGatewayFilterFactory 为请求添加Header Header的名称及值 配置说明 server:port: 8088 spring:application:name: api-gatewaycloud:nacos:discovery:server-addr: 127.0.0.1:8847username: nacos…...
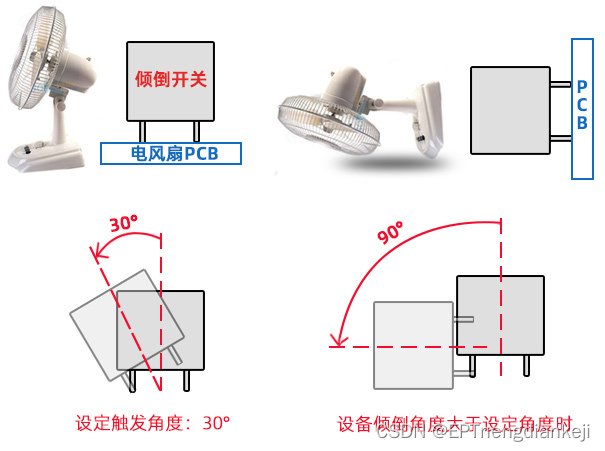
电风扇如何实现跌倒断电保护功能
电风扇作为日常生活中常用的家电产品,为了提升安全性能,在设计上通常会考虑加入跌倒断电保护功能。其中,光电倾倒开关是实现跌倒断电保护功能的关键组件之一。 光电倾倒开关内置红外发光二极管和光敏接收器,其工作原理非常巧妙。…...

编译原理总结
编译器构成 1. 前端分析部分 1.1 词法分析 确定词性,输出为token序列 1.2 语法分析 识别短语 1.3 语义分析 分析短语在句子中的成分 IR中间代码生成 2. 机器无关代码优化 3. 后端综合部分 目标代码生成 机器相关代码优化 4. 其他 全局信息表 异常输出...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
