2024最新华为OD算法题目
在一个机房中,服务器的位置标识在 n*m 的整数矩阵网格中,1表示单元格上有服务器,0 表示没有。如果两台服务器位于同一行或者同一列中紧邻的位置,则认为它们之间可以组成一个局域网。请你统计机房中最大的局域网包含的服务器个数。
输入描述
第一行输入两个正整数,n和m,0 < n,m <= 100
之后为n*m的二维数组,代表服务器信息
输出描述
最大局域网包含的服务器个数。
示例
输入
2 2
1 0
1 1
输出
3
补充说明
[0][0]、[1][0]、[1][1]三台服务器相互连接,可以组成局域网。
解法1
//练习平台:https://oj.algomooc.com/
//题目汇总:https://www.algomooc.com/3159.html
import java.util.Scanner;public class Main {static final int[][] DIRECTIONS = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};static int n, m;static int[][] grid;static boolean[][] checkList;static int area;public s相关文章:

2024最新华为OD算法题目
在一个机房中,服务器的位置标识在 n*m 的整数矩阵网格中,1表示单元格上有服务器,0 表示没有。如果两台服务器位于同一行或者同一列中紧邻的位置,则认为它们之间可以组成一个局域网。请你统计机房中最大的局域网包含的服务器个数。 输入描述 第一行输入两个正整数,n和m,…...

Redis集群方案有哪些?
今天咱们来聊聊Redis集群方案,想象一下Redis是个超级大的储物柜,里面放满了你各种各样的宝贝(数据)。但随着宝贝越来越多,一个储物柜不够用了,这时候我们就得想方设法扩大空间,还要保证找东西依…...

数字影像产业园的三大赋能:科技、创新与无限可能
数字影像产业园作为文创产业的重要载体,以科技为核心驱动力,不断推动产业的技术革新和升级。 园区内汇聚了最前沿的数字技术资源,高清摄影设备、虚拟现实技术、人工智能应用等尖端科技在这里得到广泛应用,不仅提升了生产效率&…...
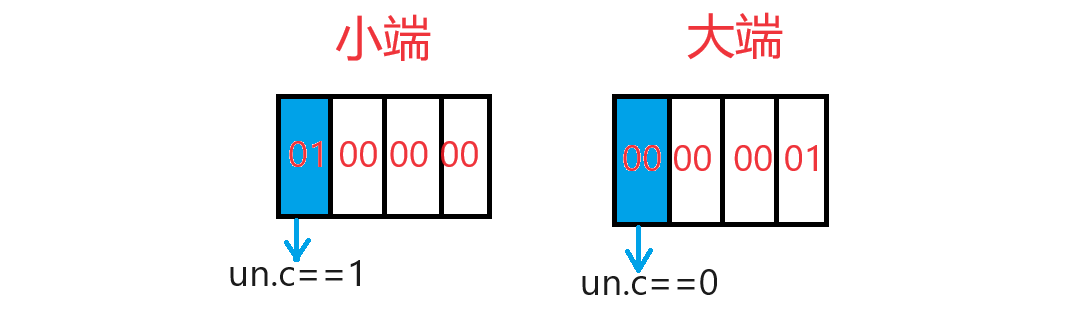
枚举(enum)+联合体(union)
枚举联合 一.枚举类型1.枚举类型的声明2.枚举类型的优点3.枚举类型的使用 二.联合体1.联合体类型的声明2.联合体的特点3.相同成员的结构体和联合体对比4.联合体大小的计算5.联合体的练习(判断大小端)6.联合体节省空间例题 一.枚举类型 1.枚举类型的声明…...

postman教程-15-前置脚本
上一小节我们学习了Postman生成随机数的方法,本小节我们讲解一下Postman前置脚本的使用方法。 Postman中的前置脚本(Pre-request Script)允许你在发送请求之前运行JavaScript代码。这可以用于修改请求头、查询参数、请求体等,或者…...

AIGC会带来失业潮吗?紧紧跟时代第一步,如何学习AIGC
会,但AI淘汰的始终是跟不上时代的人。 现在很多公司都有AI培训,不仅GPT,还有Midjourney、Stable DIffusion等一系列AI工具。 像我们公司虽然今年招的少,但也会对新招的应届生统一进行AI培训。 用任正非先生的话来说就是&#x…...
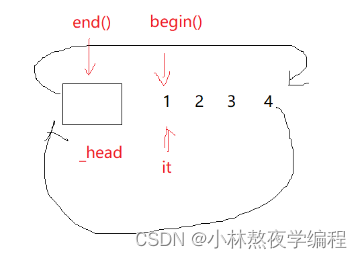
C++第二十四弹---从零开始模拟STL中的list(上)
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】【C详解】 目录 1、基本结构 2、基本函数实现 2.1、默认构造函数 2.2、尾插数据 3、迭代器的封装 3.1、迭代器的基本结构 3.2、迭代器重载函数的实现 4、迭…...
关于社情民意调查研究的内容)
大宋咨询(深圳社情民意调查)关于社情民意调查研究的内容
社情民意调查内容,是一项至关重要的社会研究活动,它涵盖了社会生活的方方面面,通过深入了解民众的需求、态度和看法,为决策提供了宝贵的参考依据。 首先,社会经济状况是社情民意调查不可或缺的一部分。这包括了对当地…...
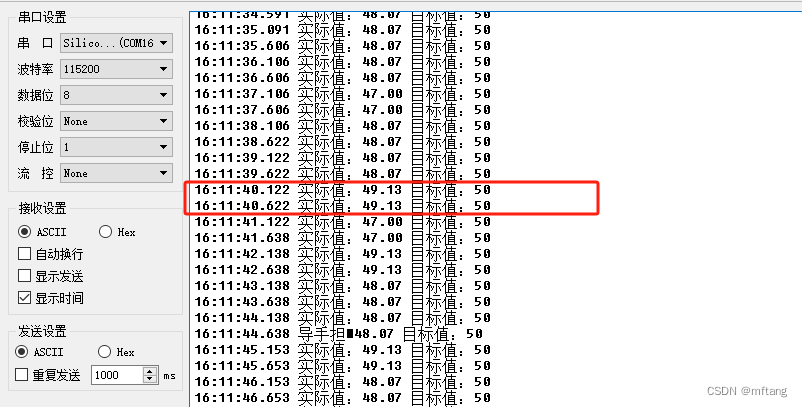
PID算法在电机速度控制上的应用
目录 概述 1 系统硬件框架 1.1 框架介绍 1.2 硬件实物图 2 STM32Cub生成工程 2.1 软件版本信息 2.2 配置参数 编辑2.3 生成项目 3 PID算法实现 3.1 概念 3.2 代码实现 4 其他功能实现 4.1 设置电机速度 4.2 PID算法控制电机 4.3 功能函数的调用 5 测试 5.1 …...

埃隆·马斯克 - 从梦想家到改变世界的企业家
埃隆马斯克 - 从梦想家到改变世界的企业家 本文内容是埃隆马斯克传的重点章节精华提炼,介绍了马斯克传奇一生 参考资料内容:埃隆马斯克传&造梦者埃隆马斯克 参考资料在文末获取,关注我,分享优质前沿资料(IT、运…...

微信小程序长图片自适应
/*wxss中的代码*/ .image-container { display:flex;width: 100%; /* 或其他需要的宽度 */ /* margin-bottom: 10px; //图片之间的间距 */height: auto; } 核心:要真正自适应,就要在wxml中加入固定宽度style“width:750rpx” /*wxml中的代码*/ &l…...

elasticsearch hanlp 插件安装操作
elasticsearch hanlp 插件安装操作 下载 hanlp 插件上传hanlp插件到elasticsearch服务器安装hanlp插件kibana测试 下载 hanlp 插件 这里大家根据自己对应的 elasticsearch 版本下载匹配版本的 hanlp 插件,由于 hanlp 及 elasticsearch 各个版本之间差别较大&#x…...

为什么进程和线程 ID 总是 4 的倍数?
如果您研究下任务管理器中的的进程 ID (PID),则你会发现这样一个规律:它们都是 4 的倍数。 基于 Windows NT 内核的操作系统上,不止是进程 ID,实际上,线程 ID (TID) 也遵守这样的规律:也即它们都是 4 的倍…...
LabVIEW版本控制
LabVIEW作为一种流行的图形化编程环境,在软件开发中广泛应用。有效地管理版本控制对于确保软件的可靠性和可维护性至关重要。LabVIEW提供了多种方式来管理VI和应用程序的修订历史,以满足不同规模和复杂度的项目需求。 LabVIEW中的VI修订历史 LabVIEW内置…...

不输Kimi的AI插件——Elmo Chat (免费,无需注册)
🌚 前阵子不是写了篇《一分钟上手AI神器——Kimi (附_ 官方提示词)》 嘛,给大伙安利了一波 Kimi Chat 这个AI 神器,不知道是不是用户量上来了,算力一下子跟不上,感觉变笨了不少🤣。在别的推文看到多轮对话后…...
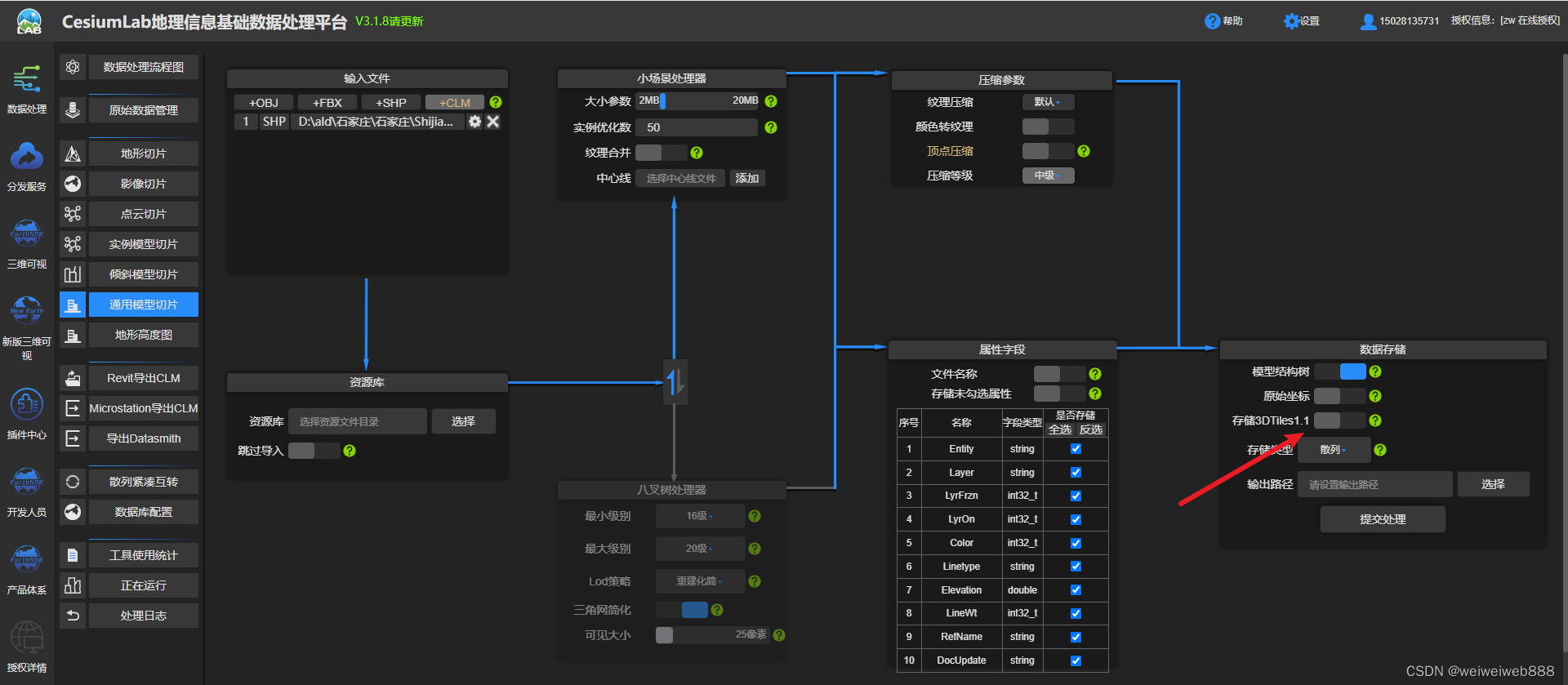
使用cesiumLab使shp转为3dtlies
过程不做赘述,网上大把,说下注意事项。 1. 存储3DTiles 选项 若是打开则输出的文件为glb格式文件,因为glb文件好储存易传输跨平台。cesium可以使用但无法处理,例如改变颜色,改着色器等。若是不打开则输出的文件为bm3d格式文件,此…...

中科数安 | 透明加密防泄密系统!如何有效防止企业内部核心数据资料外泄?
中科数安提供的透明加密防泄密系统是一种专为企业设计的数据保护解决方案,它通过以下关键特性有效防止企业内部核心数据资料外泄: PC地址:——www.weaem.com 自动智能透明加密:系统能够在操作系统级别无缝集成,对指定类…...
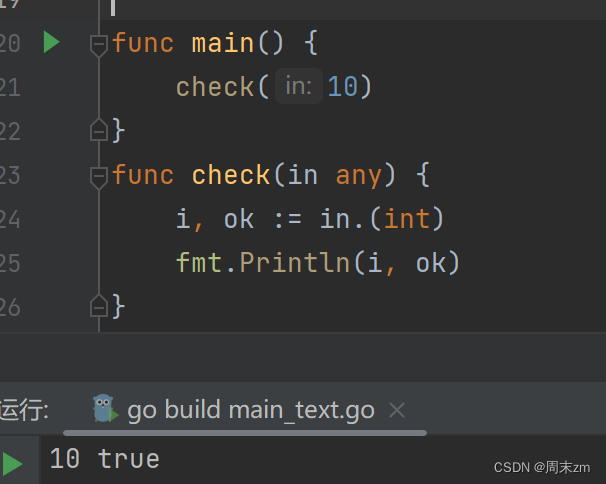
go的反射和断言
在go中对于一个变量,主要包含两个信息变量类型(type)和变量值(value) 可以通过reflect包在运行的时候动态获取变量信息,并能够进行操作 对于Type可以通过reflect.TypeOf()获取到变量的类型信息 reflect.Ty…...

打造新引擎,迈向数智金融新未来
数智技术正在全面赋能金融机构转型升级以及促进金融与实体经济的加速融合,已呈现出金融机构数智化经营加速、产业 数字金融深度融合、数字技术驱动绿色金融发展、金融信创成果涌现、金融机构加快数字化组织管理变革等行业趋势。 根据银行业协会调研,78%…...

广东智慧物流2024年端午节放假安排
广东智慧物流2024年端午节放假安排...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

英国云服务器上安装宝塔面板(BT Panel)
在英国云服务器上安装宝塔面板(BT Panel) 是完全可行的,尤其适合需要远程管理Linux服务器、快速部署网站、数据库、FTP、SSL证书等服务的用户。宝塔面板以其可视化操作界面和强大的功能广受国内用户欢迎,虽然官方主要面向中国大陆…...

git删除本地分支和远程分支
删除本地分支 git branch -d 分支名删除远程分支 git push origin --delete 分支名...
