线性模型-分类
一、线性判别分析LDA
线性判别分析是一种经典的线性学习方法,在二分类问题上最早是Fisher提出的,亦称为Fisher判别分析。
Fisher判别分析是一种用于降维和分类的统计方法,旨在找到可以最好区分不同类别的特征。它基于类内方差和类间方差的比值来选择最佳的投影方向,从而实现数据的最佳分类
思想:将训练集的样本投影到一条直线上,使得正类和反类投影在直线上的距离尽可能的分开。当测试集的样本被投影到直线上的时候,通过观察他的位置就可以知道该测试集的样本属于哪一类。
示意图

给定一个数据集D={xi,yi},Xi,μi,Σi分别表示例数集合,均值向量、协方差矩阵
投影之后再直线上的两类样本的中心点就是wTμ0和wTμ1,协方差:wTΣ0w,wTΣ1w
因为投影改变了数据的分布,所以协方差会随之改变。
就像我们之前讲到了,希望他们同类别的更接近,不同类别的就远离。其实就是最大化类中心之间的距离,最小化他们的协方差。这两个我们同时考虑的话。
将其定义为:


①类内散度矩阵
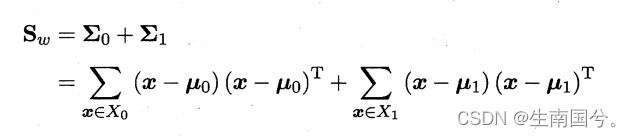
②类间散度矩阵
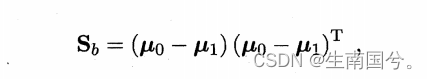
现在LDA就想要最大化目标Sb和Sw。
也叫做Sb与Sw的‘广义瑞利商’
如何确定w?
先介绍一下拉格朗日乘子法
我的理解就是:有变量,以及对于发原函数,有约束,求偏导,即求最优解

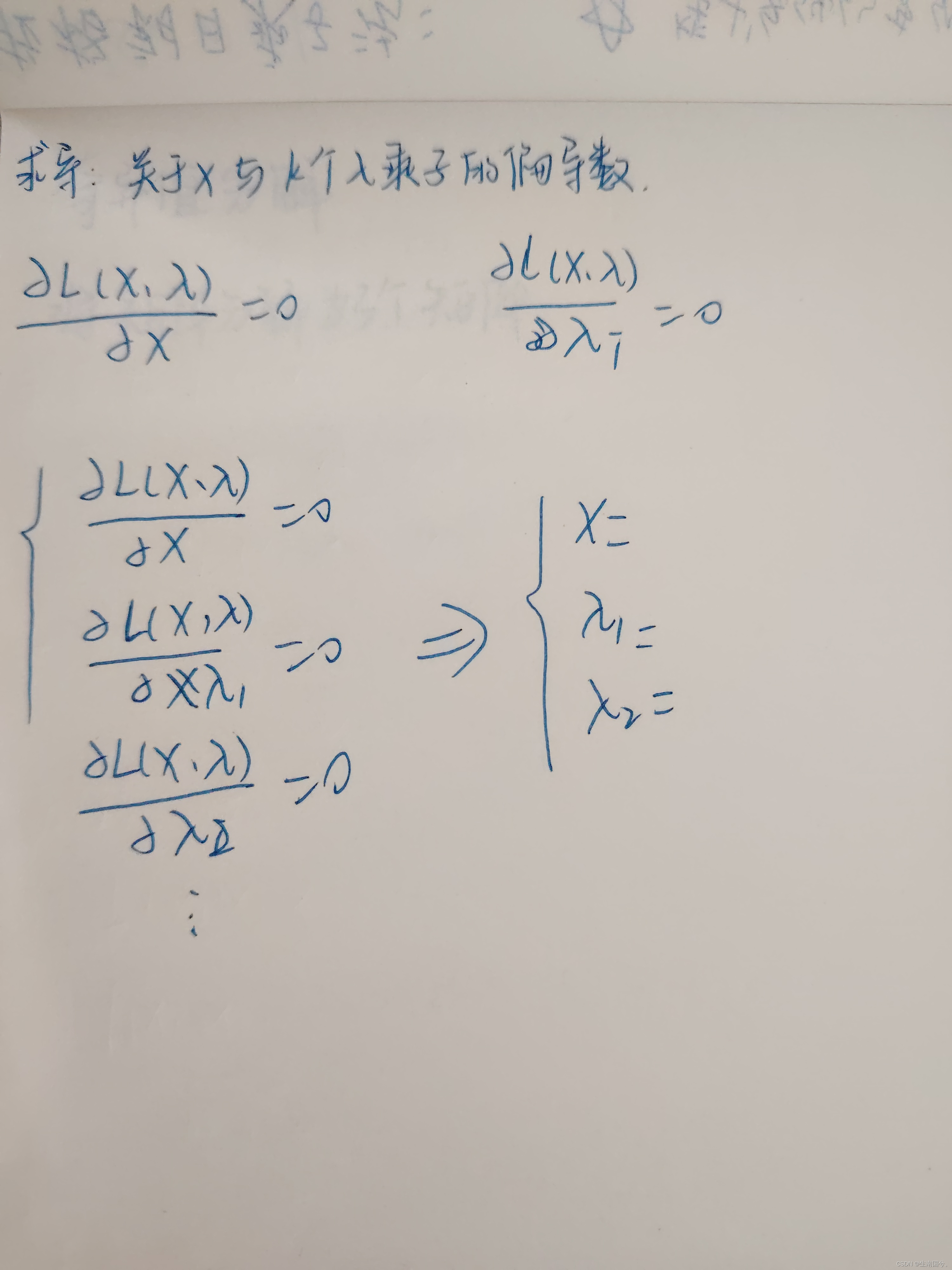
下面是对w的求解


在求解Sw的时候会使用到奇异值的分解
对于奇异值分解不太理解的可以参考这个
降维算法之奇异值分解SVD:7000字长文,看这一篇就够了!_奇异值分解降维-CSDN博客
二、多分类LDA
新定义了一个St,全局散度矩阵
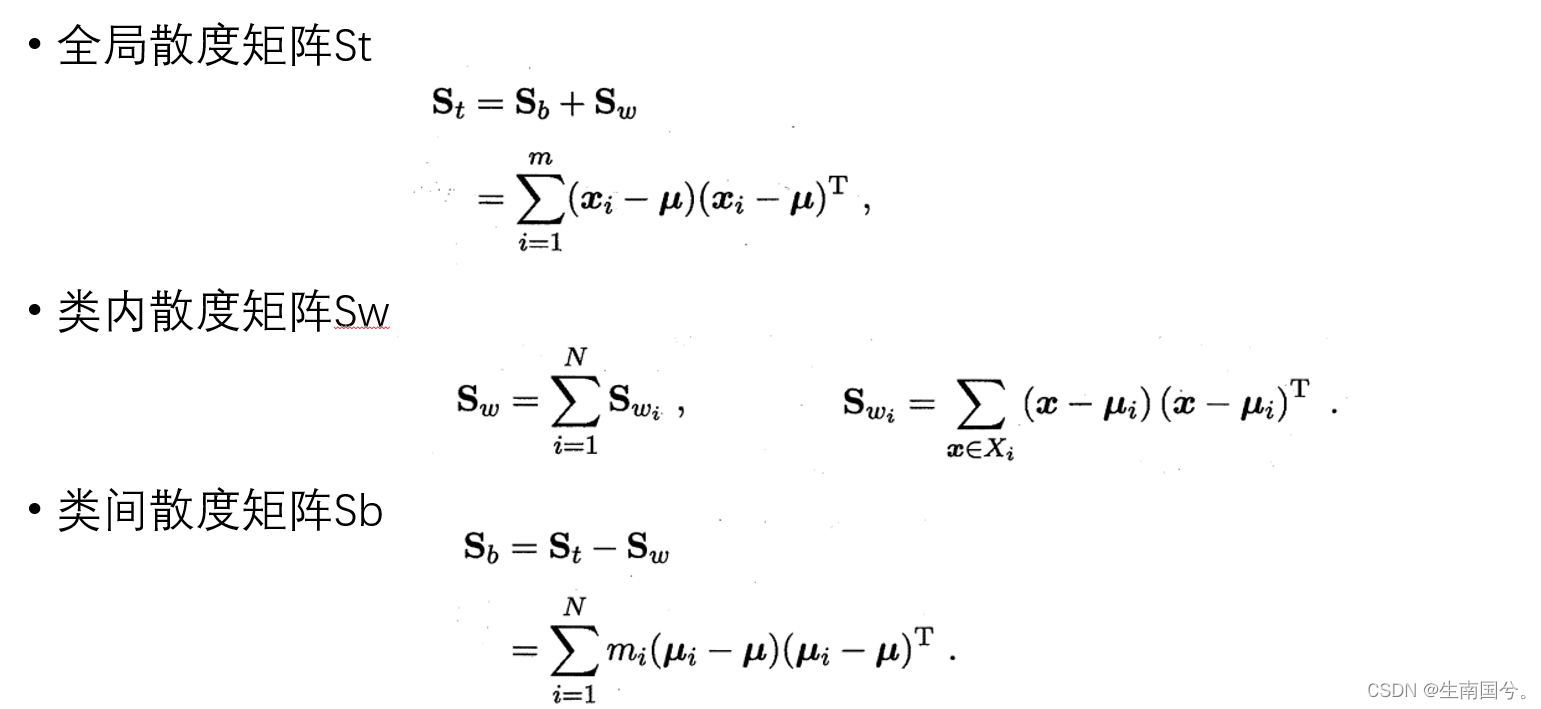
同样的要求解W
这里采用的是优化目标
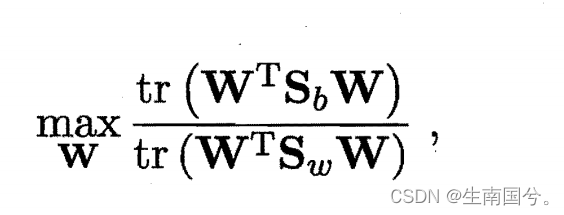
tr(·):代表矩阵的迹,是矩阵的主对角线上元素的总和。
对于多分类LDA的话就是将N个类别的投影到N-1个维度上,实现一个降维
因此,被视为一种经典的降维技术。
三、多分类学习
利用2分类策略解决多分类问题。
多分类学习的基本思路就是“拆解法“。最经典的有三种:一对一(O vs O),一对多(O vs R),多对多(M vs M).讲到这里,说不定你可以想到之前我们学过的也是类似分割的方法,对于模型评估那一块:有留出法、K折交叉验证法、自助法。
3.1 O vs O
将N个类别两两配对,看作排列组合就是,那么就会产生N(N-1)/2个二分类任务。
最终得到N(N-1)/2个分类结果,最终结果通过投票产生,即把预测的最多的类别作为最终分类结果
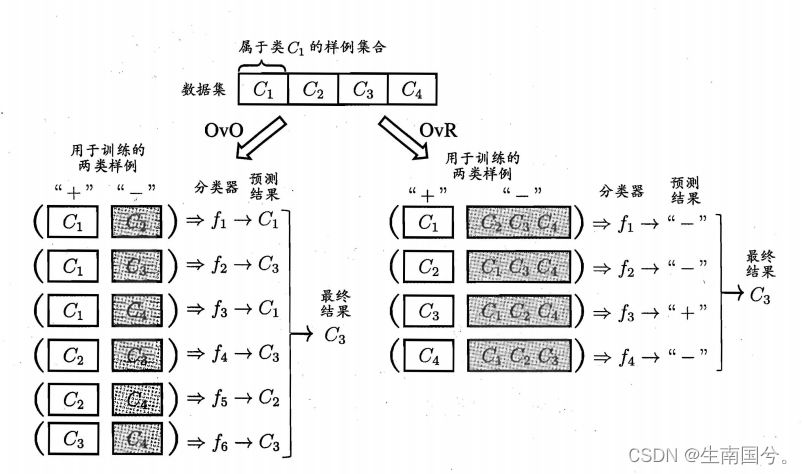
3.2 O vs R
将每一个类的样例作为正例,所有其他类的样例作为反类,训练N个分类器,在测试时若有一个分类器预测为正类,则对应的类别标记作为最终的分类结果。丢进去一个样本,若有多个分类器预测为正类,则通常考虑分类器的阈值置信度,选择置信度最大的类别标记作为分类结果。如上图。
其中,OVR需要训练N个分类器,但是OVO,却要训练N(N-1)/2个人分类器。因此一对一的存储开销和测试时间开销通常比一对多的更大,但是在训练的时候,一对多的每个分类器会使用全部的训练样本,而一对一的仅用到两个类的样本,因此在类别很多的时候,一对一的训练时间开销通常比一对多的 小。至于预测性能则却决于具体的数据分布,在多数情形下两者差不多。
3.3 M vs M
是每次将若干个类作为正类,若干个类作为反类。
但是多对多的正类和反类必须要有特殊的设计、不能随意的选取,在这里我们就介绍一种技术
纠错输出码(ECOC)
第一步:编码:
对N个类别做M次划分,每次划分将一部分类别作为正类,一部分作为反类,从而形成一个二分类发训练集,一共产生M个训练集,可以训练出M个分类器
第二部:解码:
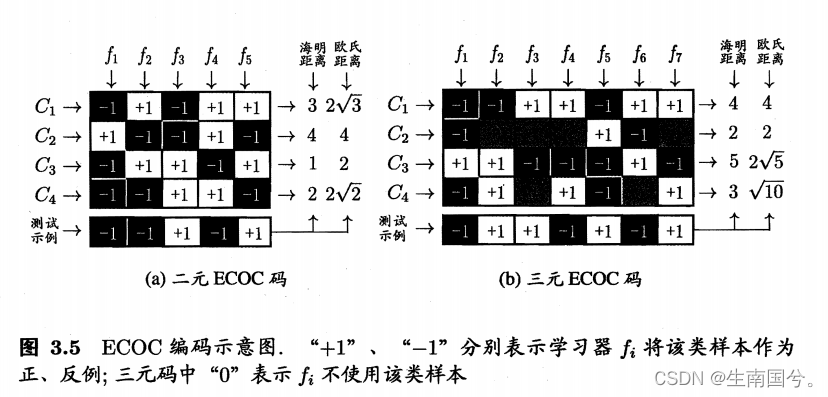
M个分类器分别对测试样本进行预测,这些预测标记组成一个编码,将这个预测编码与每个类别各自的编码进行比较,放回其中距离最小的类别作为最终预测结果
类别划分通过“编码矩阵“指定,编码矩阵有多种形式,常见的主要有——二元编码、三元编码前者将每个类别分别指定为正类和反类,后者在正类和反类之外,还指定了一个停用类。
相关文章:

线性模型-分类
一、线性判别分析LDA 线性判别分析是一种经典的线性学习方法,在二分类问题上最早是Fisher提出的,亦称为Fisher判别分析。 Fisher判别分析是一种用于降维和分类的统计方法,旨在找到可以最好区分不同类别的特征。它基于类内方差和类间方差的比…...

OpenAI前董事会成员称Sam Altman因 “ 向董事会撒谎 ” 而被解雇
据前 OpenAI 董事会成员称,据称 Altman 隐瞒了他对 OpenAI 创业基金的所有权。 更详细的内容请参考原文: https://cointelegraph.com/news/sam-altman-fired-openai-board-allegations 据一位前董事会成员称,Sam Altman 因涉嫌向董事会隐瞒…...

【启明智显分享】WIFI6开发板ZX6010:开源OpenWrt SDK,接受定制!
在数字化飞速发展的当下,网络速度和稳定性已成为各行各业不可或缺的关键因素。今天,我们为大家推荐一款基于IPQ6010的AX1800方案ZX6010 Wi-Fi6开发板,为您的网络世界注入强大动力。 一、超强硬件配置 ZX6010搭载IPQ6010四核ARM Cortex A53处…...
 函数清除多余的输⼊?)
C语言能否使⽤ fflush( ) 函数清除多余的输⼊?
一、问题 在从终端输⼊数据时,很可能会输⼊多余的数据,那么能否使⽤ fflush( ) 函数清除呢? 二、解答 fflush( ) 函数只是⽤在⽂件以写的⽅式打开时,将缓冲区内容写⼊到⽂件。因此 fflush( ) 函数仅对输出流有效,对输…...

如何把试卷上的字去掉再打印?分享三种方法
如何把试卷上的字去掉再打印?随着科技的不断发展,现代教育和学习方式也在逐渐变革。在学习过程中,我们经常需要对试卷进行整理和分析,以便更好地掌握知识点和复习。然而,传统的试卷整理方法往往效率低下且容易出错。幸…...

Android开机动画压缩包zip,自制开机动画(基于Android10.0.0-r41)
文章目录 Android开机动画压缩包zip,自制开机动画1.Android加载压缩包原理2.自制开机动画 Android开机动画压缩包zip,自制开机动画 1.Android加载压缩包原理 这里有个md文件我们看下 核心部分, 首先要创建一个文件叫做desc.txt,这是规定的…...

手机站怎么推广
随着手机的普及和移动互联网的快速发展,越来越多的人开始使用手机进行在线购物、社交娱乐、阅读资讯等,同时也催生了越来越多的手机站的出现。但是,在海量的手机站中,要让自己的手机站脱颖而出,吸引更多用户访问和使用…...

Mysql疑难报错排查 - Field ‘XXX‘ doesn‘t have a default value
项目场景: 数据库环境 :mysql8; 工程使用:MyBatisPlus 表情况: 问题描述 某一个插入语句使用了 MyBatisPlus 的 save 方法,因为end_time1 end_time2都并没有值,所以在MyBatisPlus默认情况下,…...
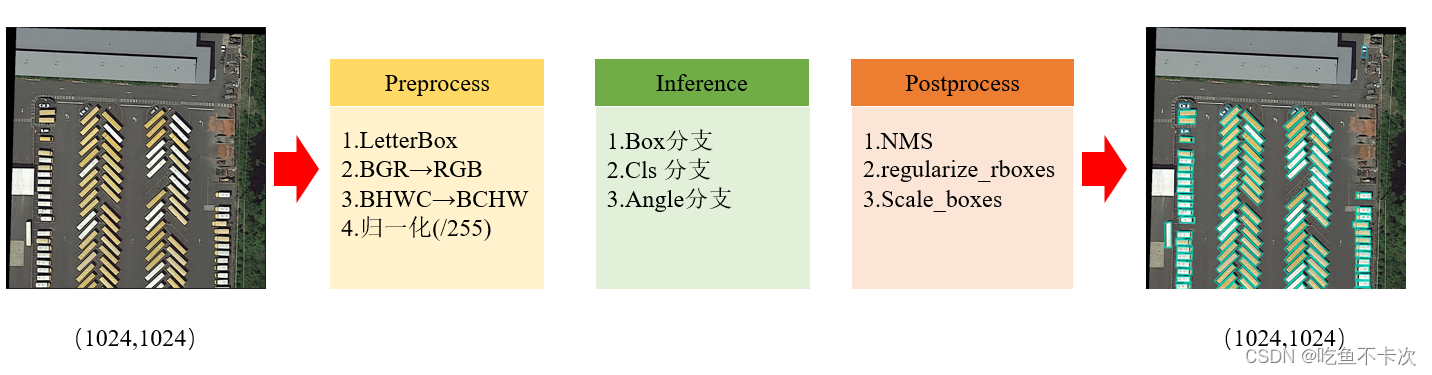
YOLOv8_obb预测流程-原理解析[旋转目标检测理论篇]
YOLOv8_obb的预测流程,主要分预处理模块、推理模块和后处理模块。这里面有很多内容是和目标检测预测流程是重合的,主要区别在于Angle分支、NMS后处理以及regularize_rboxes部分。本文也主要介绍一下这三个模块,其他模块可以结合YOLOv8预测流程-原理解析[目标检测理论篇]一起…...

02JAVA字符串和集合
1.字符串 1.String 介绍: String在java.lang包下,使用不需要导包,String代表字符串,带""字符串都是String类的对象 字符串的特点: 字符串不可变,他们的值在创建后不能被改变 字符串效果相当于(char[]),底层原理是字节数组(byte[]) String构造方法: String 变量名 ne…...
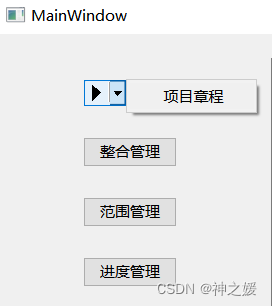
Qt如何让按钮的菜单出现在按钮的右侧
直接上代码,我们用到了一个eventfilter的函数功能。这个函数比较厉害和重要,大家务必经常拿出来看看。 void MainWindow::initMenu() { QMenu* menuLiXiang new QMenu; QAction* actXiangMuZhangCheng new QAction("项目章程"); …...

C++的类和new和delete和菱形继承机制
文章目录 参考虚函数使用虚函数的class结构相关实现源码IDA反编译子类虚表和父类虚表调用函数菱形继承 参考 https://showlinkroom.me/2017/08/21/C-%E9%80%86%E5%90%91%E5%88%86%E6%9E%90/ https://www.cnblogs.com/bonelee/p/17299985.html https://xz.aliyun.com/t/5242?t…...
:Redis的过期删除和缓存淘汰策略)
Redis教程(二十二):Redis的过期删除和缓存淘汰策略
传送门:Redis教程汇总篇,让你从入门到精通 一、过期删除策略 Redis 中的过期删除策略是与 Redis 管理键的生命周期相关的一系列操作,用于删除过期的Key以释放内存。Redis 提供了三种主要的过期删除策略: 1、惰性删除(Lazy Expiration) 工作原理:当客户端尝试访问一个…...
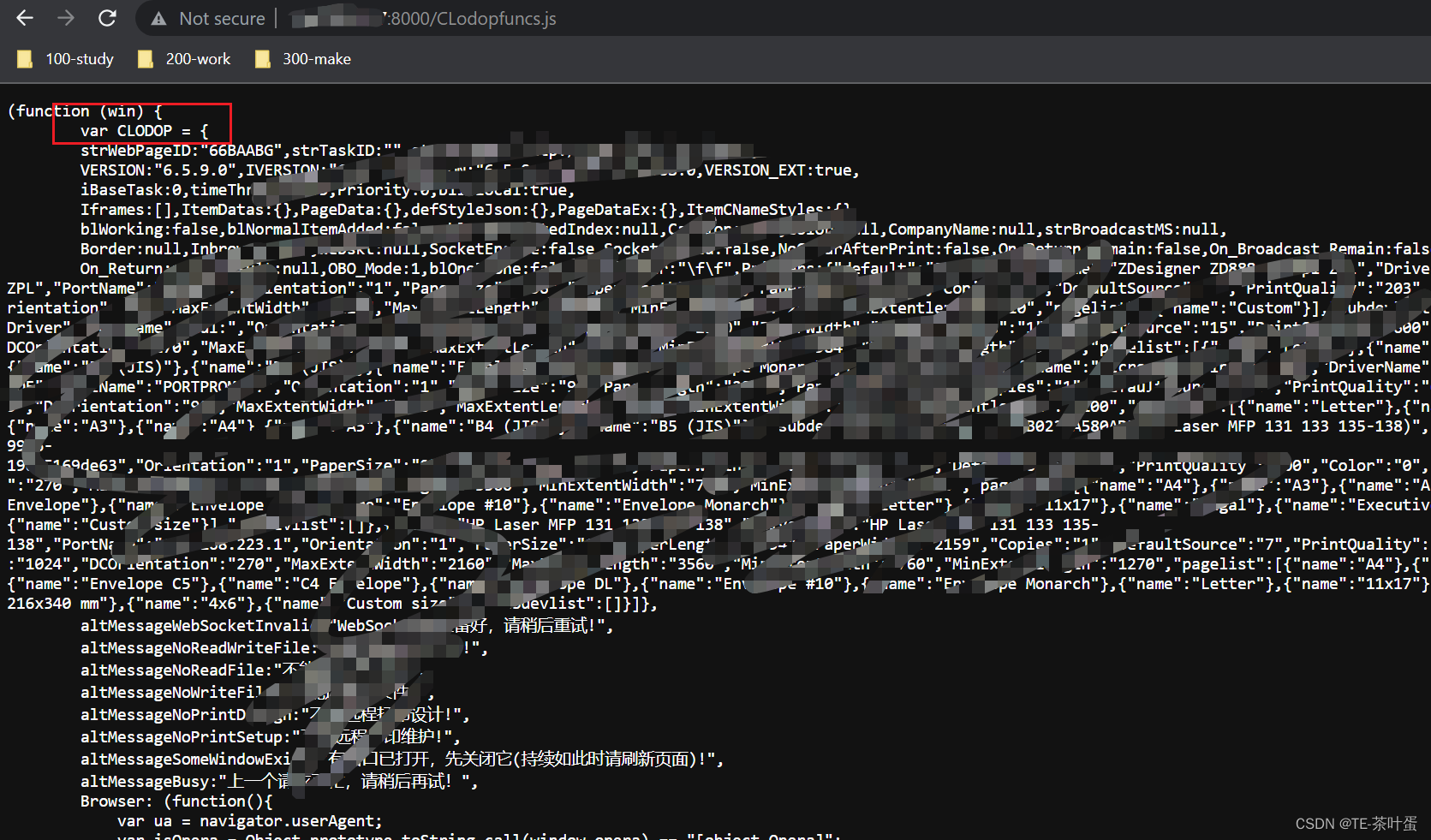
Lodop 实现局域网打印
文章目录 前言一、Lodop支持打印的方式lodop 打印方式一般有3种:本地打印局域网集中打印广域网AO打印 二、集成步骤查看lodop 插件的服务端口:查看ip后端提供接口返回ip,前端动态获取最后步骤 前言 有时候会根据不同的ip来获取资源文件&…...

HarmonyOS(二十四)——Harmonyos通用事件之触摸事件
1.触摸事件。 触摸事件是HarmonyOS通用事件的一种事件之一,当手指在组件上按下、滑动、抬起时触发。 名称是否冒泡功能描述onTouch(event: (event?: TouchEvent) > void)是手指触摸动作触发该回调,event返回值见下面TouchEvent介绍。 2. TouchEve…...

2024-前端面试的正确打开方式(GitHub火爆场景题剖析)
写在前面 最近前端面试大家有没有感觉到场景题的压迫感!!! 很显然普通面试八股不会怎么更新,而且就前端来说,面试并不是真正困难的,常规八股显示不出面试者的技术水平。 前端作为一个技术行业,…...

Vue3项目炫酷实战,检测密码强度值
在前端项目开发中,确保用户密码的强度是保护账户安全的重要措施。本文将演示如何使用Vue 3实现一个简单的密码强度检测功能。通过实时反馈,帮助用户创建更安全的密码,从而提升整体系统的安全性。无论您是前端开发新手还是经验丰富的开发者&am…...
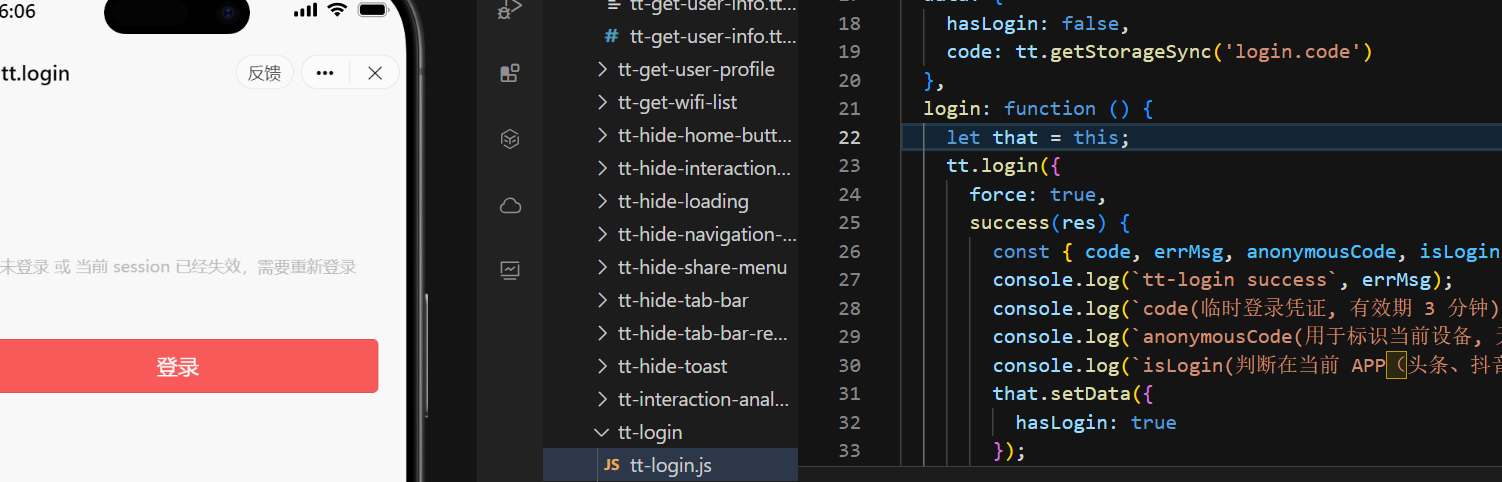
PHP实现抖音小程序用户登录获取openid
目录 第一步、抖音小程序前端使用tt.login获取code 第二步、前端拿到code传给后端 第三步、方法1 后端获取用户信息 第四步、方法2 抖音小程序拿到用户信息把用户信息传给后端 code2Session抖音小程序用户登录后端文档 第一步、抖音小程序前端使用tt.login获取code 前端 …...

Linux进程无法被kill
说明:记录一次应用进程无法被kill的错误; 场景 在一次导出MySQL数据时,使用下面的命令,将数据库数据导出为.sql文件,数据量大,导出时间长,于是我就将服务器重启了。 mysqldump -u username -…...

MySQL binlog三种模式
1.statement statement 记录的是sql语句。比如一条sql,update table_user set age 20 where id between 1 and 100。这条sql会更新100条数据,但是statement 模式下只会记录这条sql语句。 优点:不需要记录数据的变化,减少了bin …...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...
