当前位置： 首页 > news >正文

勒索软件分析_目标文件扫描行为分析

news 2025/9/16 21:03:11

BlackBasta首先通过 FindFirstVolumeW 与 FindNextVolumeW 实现系统中第一个卷的搜索和其余卷的遍历，之后通过 GetVolumePathNamesForVolumeNameW 检索指定卷的驱动器号和挂载的文件夹路径列表，然后通过 GetVolumeInformationW 获取关于指定卷的信息，具体代码如下所示。

  • FindFirstVolumeW vs. FindNextVolumeW：FindFirstVolumeW函数是Windows API中的一个函数，用于搜索计算机上的第一个卷的相关信息。它会打开一个卷搜索句柄，并返回与第一个找到的卷相关的信息。这个函数通常与FindNextVolume函数一起使用，后者用于搜索其他的卷。通过使用FindFirstVolumeW函数，我们可以枚举计算机上的所有卷，获取它们的名称以及其他属性信息。
  • GetVolumePathNamesForVolumeNameW：该函数用于检索指定卷的驱动器号和挂载的文件夹路径列表。它的功能是通过传入卷名，获取该卷对应的驱动器号以及挂载点的路径列表。这个函数的返回值是一个布尔类型，指示操作是否成功。当函数成功执行后，它会通过传入的缓冲区指针，返回驱动器号和挂载点路径的列表。返回的路径列表是以Null字符('\0')作为分隔符的字符串数组，以表示列表的结束。
  • GetVolumeInformationW：该函数的作用是获取关于指定卷的信息。这个Windows API函数可以用于检索指定卷的文件系统、卷标、序列号、每个簇的字节数、总簇数、可用簇数等信息。通过调用GetVolumeInformationW函数，可以让程序获取有关特定卷的重要信息，这在文件系统管理和数据操作中非常有用。
_DWO

相关文章：

勒索软件分析_目标文件扫描行为分析

BlackBasta首先通过 FindFirstVolumeW 与 FindNextVolumeW 实现系统中第一个卷的搜索和其余卷的遍历，之后通过 GetVolumePathNamesForVolumeNameW 检索指定卷的驱动器号和挂载的文件夹路径列表，然后通过 GetVolumeInformationW 获取关于指定卷的信息，具体代码如下所示。 Fin…...

编程日记 2024/6/6 18:15:13

2024050401-重学 Java 设计模式《实战代理模式》

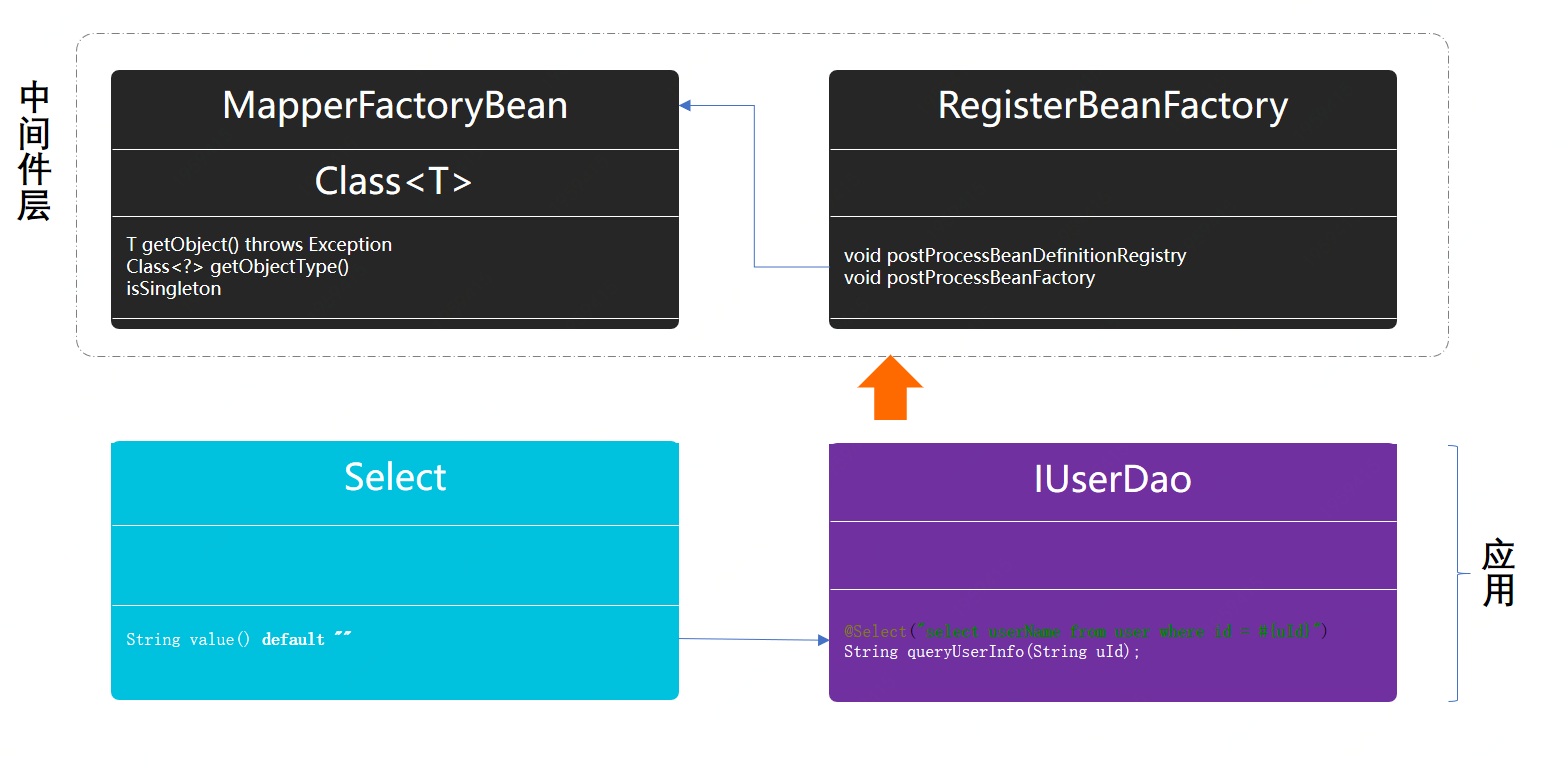
重学 Java 设计模式：实战代理模式「模拟mybatis-spring中定义DAO接口，使用代理类方式操作数据库原理实现场景」 一、前言 难以跨越的瓶颈期，把你拿捏滴死死的！ 编程开发学习过程中遇到的瓶颈期，往往是由于看不到前进…...

编程日记 2024/6/6 18:12:09

HTML跨年烟花

目录 写在前面 关于小编 HTML简介 程序设计 系列文章 写在后面 写在前面 学会了这个html烟花秀，跨年就不缺文案喽~ 关于小编 平易近人，慈眉善目，爱交朋友，舍己为人，和蔼可亲，能说会道，…...

编程日记 2024/6/6 18:11:05

微服务第二轮

学习文档 背景 由于每个微服务都有不同的地址或端口，入口不同 请求不同数据时要访问不同的入口，需要维护多个入口地址，麻烦 前端无法调用nacos，无法实时更新服务列表 单体架构时我们只需要完成一次用户登录、身份校验&#xff…...

编程日记 2024/6/6 18:10:04

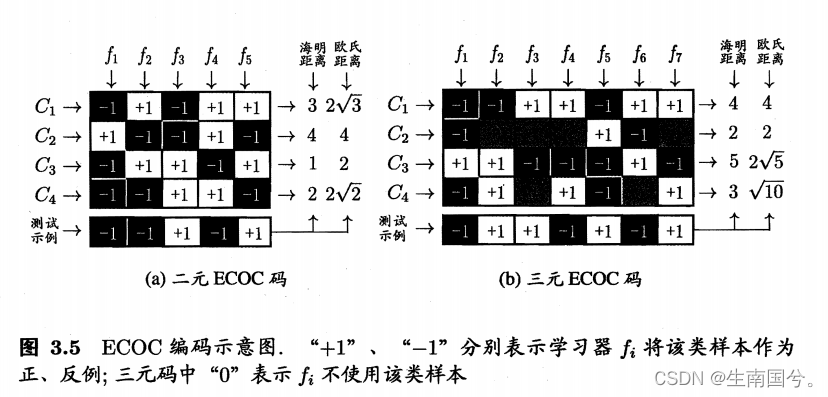
线性模型-分类

一、线性判别分析LDA 线性判别分析是一种经典的线性学习方法，在二分类问题上最早是Fisher提出的，亦称为Fisher判别分析。 Fisher判别分析是一种用于降维和分类的统计方法，旨在找到可以最好区分不同类别的特征。它基于类内方差和类间方差的比…...

编程日记 2024/6/6 18:08:02

OpenAI前董事会成员称Sam Altman因 “ 向董事会撒谎 ” 而被解雇

据前 OpenAI 董事会成员称，据称 Altman 隐瞒了他对 OpenAI 创业基金的所有权。 更详细的内容请参考原文： https://cointelegraph.com/news/sam-altman-fired-openai-board-allegations 据一位前董事会成员称，Sam Altman 因涉嫌向董事会隐瞒…...

编程日记 2024/6/6 18:06:00

【启明智显分享】WIFI6开发板ZX6010：开源OpenWrt SDK,接受定制！

在数字化飞速发展的当下，网络速度和稳定性已成为各行各业不可或缺的关键因素。今天，我们为大家推荐一款基于IPQ6010的AX1800方案ZX6010 Wi-Fi6开发板，为您的网络世界注入强大动力。 一、超强硬件配置 ZX6010搭载IPQ6010四核ARM Cortex A53处…...

编程日记 2024/6/6 18:04:59

C语言能否使⽤ fflush( ) 函数清除多余的输⼊？

一、问题 在从终端输⼊数据时，很可能会输⼊多余的数据，那么能否使⽤ fflush( ) 函数清除呢？ 二、解答 fflush( ) 函数只是⽤在⽂件以写的⽅式打开时，将缓冲区内容写⼊到⽂件。因此 fflush( ) 函数仅对输出流有效，对输…...

编程日记 2024/6/6 18:03:58

如何把试卷上的字去掉再打印？分享三种方法

如何把试卷上的字去掉再打印？随着科技的不断发展，现代教育和学习方式也在逐渐变革。在学习过程中，我们经常需要对试卷进行整理和分析，以便更好地掌握知识点和复习。然而，传统的试卷整理方法往往效率低下且容易出错。幸…...

编程日记 2024/6/6 18:02:57

Android开机动画压缩包zip，自制开机动画(基于Android10.0.0-r41)

文章目录 Android开机动画压缩包zip，自制开机动画1.Android加载压缩包原理2.自制开机动画 Android开机动画压缩包zip，自制开机动画 1.Android加载压缩包原理 这里有个md文件我们看下 核心部分, 首先要创建一个文件叫做desc.txt，这是规定的…...

编程日记 2024/6/6 17:59:52

手机站怎么推广

随着手机的普及和移动互联网的快速发展，越来越多的人开始使用手机进行在线购物、社交娱乐、阅读资讯等，同时也催生了越来越多的手机站的出现。但是，在海量的手机站中，要让自己的手机站脱颖而出，吸引更多用户访问和使用…...

编程日记 2024/6/6 17:58:50

Mysql疑难报错排查 - Field ‘XXX‘ doesn‘t have a default value

项目场景： 数据库环境 ：mysql8; 工程使用：MyBatisPlus 表情况： 问题描述 某一个插入语句使用了 MyBatisPlus 的 save 方法，因为end_time1 end_time2都并没有值，所以在MyBatisPlus默认情况下，…...

编程日记 2024/6/6 17:57:48

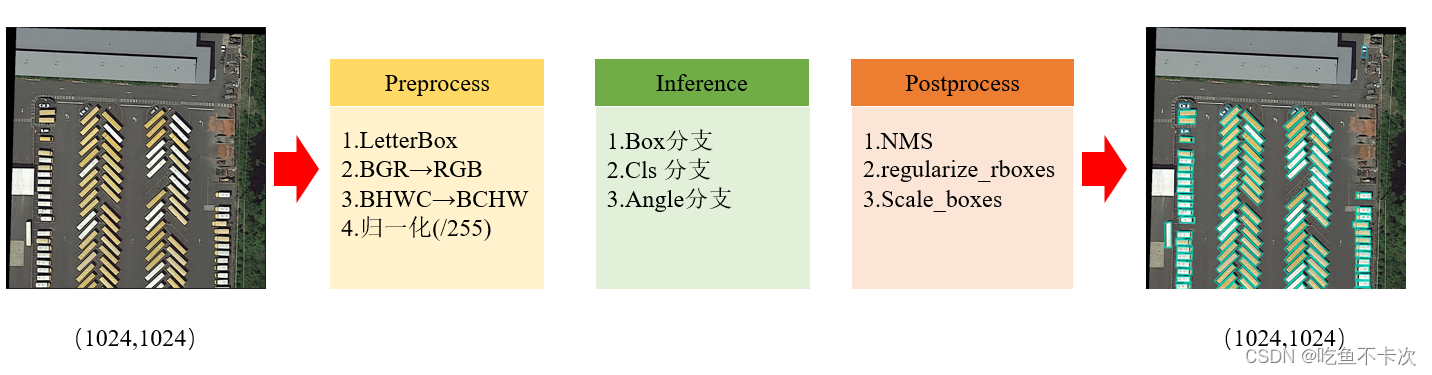
YOLOv8_obb预测流程-原理解析[旋转目标检测理论篇]

YOLOv8_obb的预测流程，主要分预处理模块、推理模块和后处理模块。这里面有很多内容是和目标检测预测流程是重合的，主要区别在于Angle分支、NMS后处理以及regularize_rboxes部分。本文也主要介绍一下这三个模块，其他模块可以结合YOLOv8预测流程-原理解析[目标检测理论篇]一起…...

编程日记 2024/6/6 17:55:46

02JAVA字符串和集合

1.字符串 1.String 介绍: String在java.lang包下,使用不需要导包,String代表字符串,带""字符串都是String类的对象 字符串的特点: 字符串不可变,他们的值在创建后不能被改变 字符串效果相当于(char[]),底层原理是字节数组(byte[]) String构造方法: String 变量名 ne…...

编程日记 2024/6/6 17:54:44

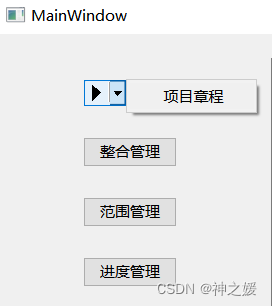
Qt如何让按钮的菜单出现在按钮的右侧

直接上代码，我们用到了一个eventfilter的函数功能。这个函数比较厉害和重要，大家务必经常拿出来看看。 void MainWindow::initMenu() { QMenu* menuLiXiang new QMenu; QAction* actXiangMuZhangCheng new QAction("项目章程"); …...

编程日记 2024/6/6 17:53:44

C++的类和new和delete和菱形继承机制

文章目录 参考虚函数使用虚函数的class结构相关实现源码IDA反编译子类虚表和父类虚表调用函数菱形继承 参考 https://showlinkroom.me/2017/08/21/C-%E9%80%86%E5%90%91%E5%88%86%E6%9E%90/ https://www.cnblogs.com/bonelee/p/17299985.html https://xz.aliyun.com/t/5242?t…...

编程日记 2024/6/6 17:50:40

Redis教程(二十二)：Redis的过期删除和缓存淘汰策略

传送门：Redis教程汇总篇，让你从入门到精通 一、过期删除策略 Redis 中的过期删除策略是与 Redis 管理键的生命周期相关的一系列操作，用于删除过期的Key以释放内存。Redis 提供了三种主要的过期删除策略： 1、惰性删除（Lazy Expiration） 工作原理：当客户端尝试访问一个…...

编程日记 2024/6/6 17:49:39

Lodop 实现局域网打印

文章目录 前言一、Lodop支持打印的方式lodop 打印方式一般有3种：本地打印局域网集中打印广域网AO打印 二、集成步骤查看lodop 插件的服务端口：查看ip后端提供接口返回ip，前端动态获取最后步骤 前言 有时候会根据不同的ip来获取资源文件&…...

编程日记 2024/6/6 17:47:35

HarmonyOS（二十四）——Harmonyos通用事件之触摸事件

1.触摸事件。 触摸事件是HarmonyOS通用事件的一种事件之一，当手指在组件上按下、滑动、抬起时触发。 名称是否冒泡功能描述onTouch(event: (event?: TouchEvent) > void)是手指触摸动作触发该回调，event返回值见下面TouchEvent介绍。 2. TouchEve…...

编程日记 2024/6/6 17:46:34

2024-前端面试的正确打开方式（GitHub火爆场景题剖析）

写在前面 最近前端面试大家有没有感觉到场景题的压迫感！！！ 很显然普通面试八股不会怎么更新，而且就前端来说，面试并不是真正困难的，常规八股显示不出面试者的技术水平。 前端作为一个技术行业&#xff0c…...

编程日记 2024/6/6 17:45:34

k8s从入门到放弃之Ingress七层负载

k8s从入门到放弃之Ingress七层负载 在Kubernetes（简称K8s）中，Ingress是一个API对象，它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress，你可…...

编程新知 2025/9/7 0:12:53

MFC内存泄露

1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

编程新知 2025/9/13 17:44:01

多场景 OkHttpClient 管理器 - Android 网络通信解决方案

下面是一个完整的 Android 实现&#xff0c;展示如何创建和管理多个 OkHttpClient 实例&#xff0c;分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

编程新知 2025/8/6 7:06:58

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖

在前面的练习中&#xff0c;每个页面需要使用ref&#xff0c;onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入&#xff0c;需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

编程新知 2025/9/14 18:41:15

定时器任务——若依源码分析

分析util包下面的工具类schedule utils&#xff1a; ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类&#xff0c;封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz&#xff0c;先构建任务的 JobD…...

编程新知 2025/9/14 12:35:14

【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张（Windows/Linux）

要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况&#xff0c;可以通过以下几种方式模拟或触发&#xff1a; 1. 增加CPU负载 运行大量计算密集型任务&#xff0c;例如&#xff1a; 使用多线程循环执行复杂计算&#xff08;如数学运算、加密解密等&#xff09;。运行图…...

编程新知 2025/8/22 22:34:43

初学 pytest 记录

安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

编程新知 2025/9/9 10:09:57

R语言速释制剂QBD解决方案之三

本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

编程新知 2025/9/2 17:53:12

第7篇：中间件全链路监控与 SQL 性能分析实践

7.1 章节导读 在构建数据库中间件的过程中&#xff0c;可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中&#xff0c;必须做到&#xff1a; &#x1f50d; 追踪每一条 SQL 的生命周期&#xff08;从入口到数据库执行&#xff09;&#…...

编程新知 2025/8/8 6:07:28

MySQL的pymysql操作

本章是MySQL的最后一章&#xff0c;MySQL到此完结&#xff0c;下一站Hadoop&#xff01;&#xff01;&#xff01; 这章很简单&#xff0c;完整代码在最后&#xff0c;详细讲解之前python课程里面也有&#xff0c;感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

编程新知 2025/9/5 23:31:07