AMD显卡和英伟达显卡哪个好?
显卡是计算机中负责处理图形和视频输出的硬件设备,主要分为两种类型:AMD的A卡和NVIDIA的N卡。那么AMD显卡和英伟达显卡哪个好?怎么选?
答:不能一概而论地说哪个好,因为它们各有优势,选择应基于个人需求和预算。
1、架构:AMD和NVIDIA的显卡都采用不同的架构。AMD的GCN架构已经使用多年,虽然在早期非常先进,但近年来更新不如NVIDIA频繁。NVIDIA的显卡架构更新较快,例如推出了专为光线追踪和AI计算设计的Ampere架构。这两种架构在性能和功耗方面有所不同。

2、性能:AMD和NVIDIA的显卡在性能上也有所不同。
AMD显卡通常被认为在性价比方面表现较好,尤其是在中端到高端产品中,如RX 6700XT到RX 7900XT,提供了相对更高的性能提升。
在一些游戏和应用程序中,NVIDIA的显卡可能表现更好,尤其NVIDIA显卡在AI、深度学习等专业领域拥有更强的优势,特别是在CUDA核心和Tensor核心的支持下,为加速计算提供了强大的性能。而在另一些应用程序中,AMD的显卡可能表现更好。这取决于应用程序的优化和显卡的硬件规格。

3、价格:一般来说,AMD的显卡比NVIDIA的显卡更便宜。这是因为AMD的显卡生产商在硬件上采用的是更多的核心和更少的封装,这可以使得价格更加合理。但如果追求最高端的游戏体验,NVIDIA的RTX系列显卡则是更佳的选择。
4、特殊功能:AMD和NVIDIA的显卡在特殊功能上也有所不同。例如,NVIDIA的显卡支持实时光线追踪技术,而AMD的显卡则支持FidelityFX超解析技术。这些特殊功能可以提高显卡在特定应用程序中的性能和质量。
总的来说:
如果只是想要打游戏,那么AMD显卡性价比更高,英伟达显卡极致性能更好;
如果还需要专业3d渲染、图形等工作,那么一定要用英伟达显卡。

相关文章:

AMD显卡和英伟达显卡哪个好?
显卡是计算机中负责处理图形和视频输出的硬件设备,主要分为两种类型:AMD的A卡和NVIDIA的N卡。那么AMD显卡和英伟达显卡哪个好?怎么选? 答:不能一概而论地说哪个好,因为它们各有优势,选择应基于…...
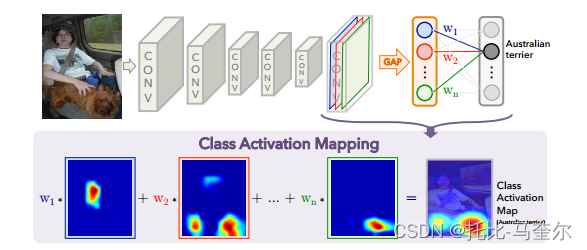
5.31.8 学习深度特征以实现判别定位
1. 介绍 尽管没有对物体的位置提供监督,但卷积神经网络 (CNN) 各层的卷积单元实际上可以充当物体检测器。尽管卷积层具有这种出色的物体定位能力,但当使用全连接层进行分类时,这种能力就会丧失。最近,一些流行的全卷积神经网络,如 Network in Network (NIN) [13] 和 Goog…...

uniapp小程序多线程 Worker 实战【2024】
需求 最近遇到个小程序异步解码的需求,采用了WebAssembly,涉及大量的计算。由于小程序的双线程模型只有一个线程处理数据,因此智能寻求其它的解决方案。查看小程序的文档,发现小程序还提供一个异步线程的Worker方案,可…...

C语言基础——数组(2)
ʕ • ᴥ • ʔ づ♡ど 🎉 欢迎点赞支持🎉 个人主页:励志不掉头发的内向程序员; 专栏主页:C语言基础; 文章目录 前言 一、二维数组的创建 1.1 二维数组的概念 1.2二维数组的创建 二、二维数组…...

封装PHP用于发送GET和POST请求的公共方法
封装了ThinkPHP用于发送GET和POST请求的公共方法。这个方法可以放在你的公共函数文件中,或者创建一个独立的类来管理这些请求。 <?php namespace app\common\utils;use think\facade\Log; use think\exception\HttpException;class HttpRequest {/*** 发送GET请…...

MongoDB~基础知识记录
为何要学Mongodb 工作以来,使用最多、了解最多的是MySQL。但技术的发展一定是依据痛点来的,就比如我遇到的痛点,一个业务、一个平台能力、存储的一个对象,随着产品和运营的需求,不断的进行变更,每一次的变…...
DSP28335模块配置模板系列——ADC配置模板
一、配置步骤 1.使能并配置高速时钟HSPCLK、ADC校验 EALLOW;SysCtrlRegs.PCLKCR0.bit.ADCENCLK 1; EDIS;EALLOW;SysCtrlRegs.HISPCP.all ADC_MODCLK; // HSPCLK SYSCLKOUT/(2*ADC_MODCLK)ADC_cal();EDIS; 这里ADC_MODCLK3,所以HSPCLK时钟为150/625Mhz 2.配…...
)
字符串转换为字节数组、16进制转换为base64、base64转换为字符串数组、base64转换为16进制(微信小程序)
1、字符串转换为字节数组 // 字符串转为字节数组 function stringToByteArray(str) {var array new Uint8Array(str.length);for (var i 0; i < str.length; i) {array[i] str.charCodeAt(i);}return array; } 2、16进制转换为base64 // 16进制转换为base64 function H…...
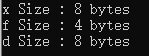
c++中, 直接写浮点数, 是float 还是 double?
如果直接一个浮点数, 那么他默认是float还是double呢? 测试用例 #include <iostream> using namespace std;int main() {auto x 0.2;float f 0.2;double d 0.2;cout << "x Size : " << sizeof(x) << " bytes" << endl…...

C++核心编程友元的应用
文章目录 1.友元1.什么是友元2.全局函数做友元2.类做友元3.成员函数做友元 1.友元 1.什么是友元 在C中,友元(friend)是一种允许一个类或函数访问另一个类的非公有(private 或 protected)成员的机制。这种机制打破了类…...

C#,JavaScript实现浮点数格式化自动保留合适的小数位数
目标 由于浮点数有漂移问题,转成字符串时 3.6 有可能得到 3.6000000000001,总之很长的一串,通常需要截取,但按照固定长度截取不一定能使用各种情况,如果能根据数值大小保留有效位数就好了。 C#实现 我们可以在基础库里…...

Android基础-工程目录结构说明
Android工程的项目目录结构是开发Android应用时的基础,它组织和存储了应用的所有源代码、资源和配置文件。了解并熟悉这个目录结构对于提高开发效率和代码管理至关重要。下面将详细阐述Android工程的项目目录结构。 1. 工程根目录 Android工程的根目录通常包含多个…...

浅谈提示词发展现状,Prompt 自动优化是未来。
#封面手绘于本科期间,当年在知乎上写的第一篇关于 AI 的文章就用的这个封面,聊表纪念。 这次我们来聊聊 Prompt. 本来想取一个类似“提示词不存在了…”,或是“再见,Prompt 课程…”的标题,但最近很多大佬的谬赞让我感…...

揭秘智能测径仪省钱之道!每年能为每条产线省上百万!
在当今竞争激烈的市场环境下,企业们都在不断寻求提高生产效率、降低成本的方法。而智能测径仪的出现,为圆形钢材、螺纹钢等生产企业实现这一目标提供了有力的支持。 智能测径仪被广泛应用于高线、铸管、圆钢、螺纹钢、钢筋等的轧制生产线中,进…...
echaerts图例自动滚动并隐藏翻页按钮
效果图 代码 legend: {itemHeight: 14,itemWidth: 14,height: "300", //决定显示多少个// 通过 CSS 完全隐藏翻页按钮pageButtonItemGap: 0,pageButtonPosition: end,pageIconColor: transparent, // 隐藏翻页按钮pageIconInactiveColor: transparent, // 隐藏翻页按…...
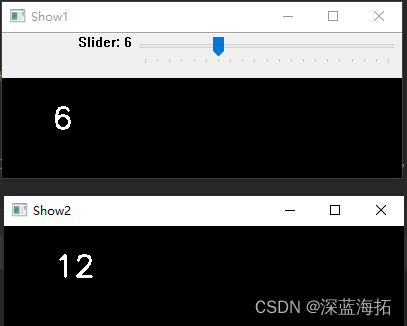
OpenCV的小部件最基本范例
OpenCV也有与PYQT类似的小部件,例如滑块slider。OpenCV可以用与PYQT类似的“信号与槽”方法,也可以在函数中直接查询小部件的值。 import cv2 import numpy as npcv2.namedWindow(Show1) image np.zeros((100, 400, 3), np.uint8) # 创建一个空白内容…...

内置类型知多少?
内置类型(也称为基本类型或原生类型)是C/C本身定义的数据类型,它们直接由编译器支持,不需要用户自定义。 内置类型主要包括以下几类: 1.算术类型: (1)整型:int、short、long、lon…...
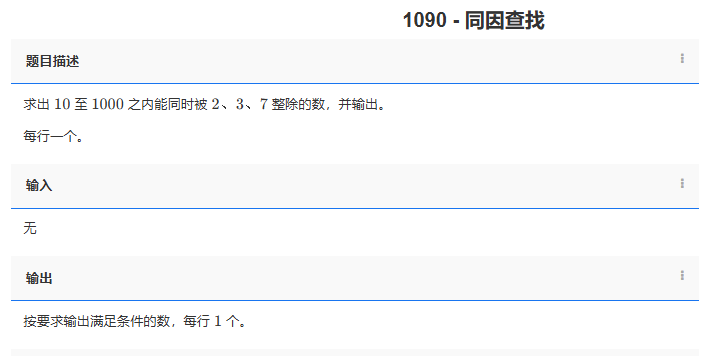
【C++题解】1090 - 同因查找
问题:1090 - 同因查找 类型:for循环、简单循环 题目描述: 求出 10 至 1000 之内能同时被2、3、7 整除的数,并输出。 每行一个。 输入: 无。 输出: 按要求输出满足条件的数,每行 1 个。 完…...
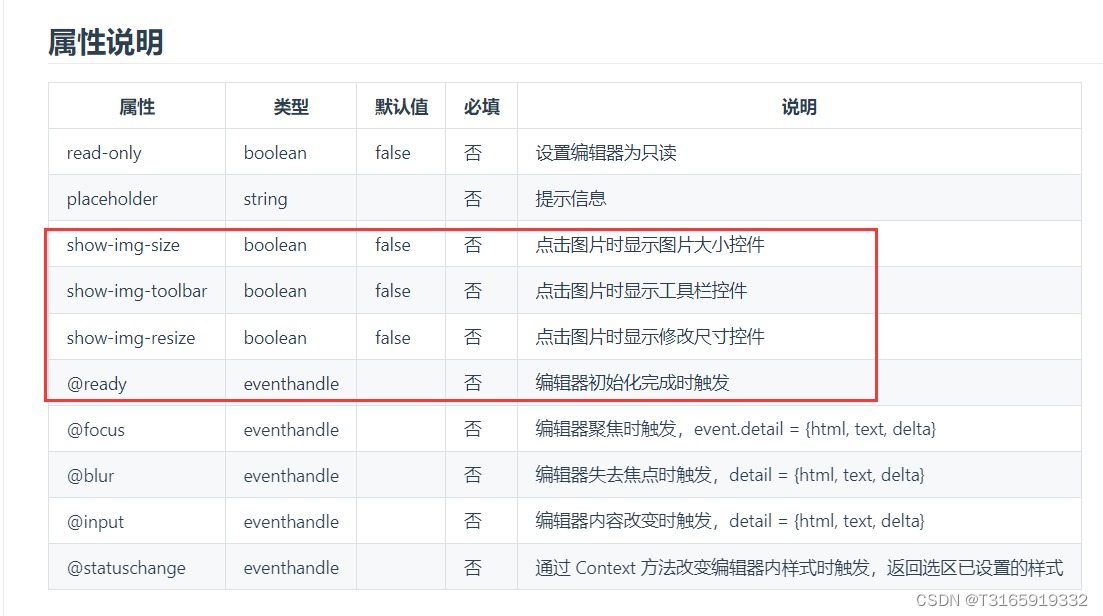
uni微信小程序editor富文本组件如何插入图片
需求 在editor中插入图片,并对图片进行编辑,简略看一下组件的属性,官网editor 组件 | uni-app官网 解决方案 首先要使用到ready这个属性,然后官网有给代码粘过来,简单解释一下这段代码的意思(作用是在不同…...

LabVIEW调用国产硬件DLL的稳定性问题及解决方案
在LabVIEW中调用国内公司提供的硬件DLL时,尽管可以运行,但常出现不稳定和bug问题,且厂家临时修改的版本未经长期测试。为确保稳定性和质量,需要制定系统化的测试和反馈机制、建立严格的版本控制、与厂家协作优化、并进行深入的自测…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...

Netty自定义协议解析
目录 自定义协议设计 实现消息解码器 实现消息编码器 自定义消息对象 配置ChannelPipeline Netty提供了强大的编解码器抽象基类,这些基类能够帮助开发者快速实现自定义协议的解析。 自定义协议设计 在实现自定义协议解析之前,需要明确协议的具体格式。例如,一个简单的…...
