回溯法——力扣题型全解【更新中】
(本文源自网上教程的笔记)
回溯基础理论
回溯搜索法,它是一种搜索的方式。
回溯是递归的副产品,只要有递归就会有回溯。
所以以下讲解中,回溯函数也就是递归函数,指的都是一个函数。
回溯法的效率
虽然回溯法很难,很不好理解,但是回溯法并不是什么高效的算法。
因为回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,如果想让回溯法高效一些,可以加一些剪枝的操作,但也改不了回溯法就是穷举的本质。
那么既然回溯法并不高效为什么还要用它呢?
因为没得选,一些问题能暴力搜出来就不错了,撑死了再剪枝一下,还没有更高效的解法。
此时大家应该好奇了,都什么问题,这么牛逼,只能暴力搜索。
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
什么是组合,什么是排列?
组合是不强调元素顺序的,排列是强调元素顺序。
例如:{1, 2} 和 {2, 1} 在组合上,就是一个集合,因为不强调顺序,而要是排列的话,{1, 2} 和 {2, 1} 就是两个集合了。
如何理解回溯法
因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度,这就构成的树的深度。
回溯函数伪代码如下:
void backtracking(参数)
- 回溯函数终止条件
既然是树形结构,那么我们在讲解二叉树的递归 (opens new window)的时候,就知道遍历树形结构一定要有终止条件。
所以回溯也有要终止条件。
什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
所以回溯函数终止条件伪代码如下:
if (终止条件) {存放结果;return;
}- 回溯搜索的遍历过程
在上面我们提到了,回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度。
如图:

注意图中,我特意举例集合大小和孩子的数量是相等的!
回溯函数遍历过程伪代码如下:
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果
}
for循环就是遍历集合区间,可以理解一个节点有多少个孩子,这个for循环就执行多少次。
backtracking这里自己调用自己,实现递归。
大家可以从图中看出for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了。
分析完过程,回溯算法模板框架如下:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}这份模板很重要,后面做回溯法的题目都靠它了!
77.组合

直接的解法当然是使用for循环,例如示例中k为2,很容易想到 用两个for循环,这样就可以输出 和示例中一样的结果。
代码如下:


递归来做层叠嵌套(可以理解是开k层for循环),每一次的递归中嵌套一个for循环,那么递归就可以用于解决多层嵌套循环的问题了。
此时递归的层数大家应该知道了,例如:n为100,k为50的情况下,就是递归50层。
为方便理解,可以用树形结构来理解
回溯法解决的问题都可以抽象为树形结构(N叉树),用树形结构来理解回溯就容易多了。
那么我把组合问题抽象为如下树形结构:

看出这棵树,一开始集合是 1,2,3,4, 从左向右取数,取过的数,不再重复取。
第一次取1,集合变为2,3,4 ,因为k为2,我们只需要再取一个数就可以了,分别取2,3,4,得到集合[1,2] [1,3] [1,4],以此类推。
每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围。
图中可以发现n相当于树的宽度,k相当于树的深度。
那么如何在这个树上遍历,然后收集到我们要的结果集呢?
图中每次搜索到了叶子节点,我们就找到了一个结果。
相当于只需要把达到叶子节点的结果收集起来,就可以求得 n个数中k个数的组合集合。
其实不定义这两个全局变量也是可以的,把这两个变量放进递归函数的参数里,但函数里参数太多影响可读性,所以我定义全局变量了。
函数里一定有两个参数,既然是集合n里面取k个数,那么n和k是两个int型的参数。
然后还需要一个参数,为int型变量startIndex,这个参数用来记录本层递归的中,集合从哪里开始遍历(集合就是[1,...,n] )。
为什么要有这个startIndex呢?
startIndex 就是防止出现重复的组合。
从下图中红线部分可以看出,在集合[1,2,3,4]取1之后,下一层递归,就要在[2,3,4]中取数了,那么下一层递归如何知道从[2,3,4]中取数呢,靠的就是startIndex。

所以需要startIndex来记录下一层递归,搜索的起始位置。
那么整体代码如下:
vector<vector<int>> result; // 存放符合条件结果的集合
vector<int> path; // 用来存放符合条件单一结果
void backtracking(int n, int k, int startIndex)
- 回溯函数终止条件
什么时候到达所谓的叶子节点了呢?
path这个数组的大小如果达到k,说明我们找到了一个子集大小为k的组合了,在图中path存的就是根节点到叶子节点的路径。
如图红色部分:

此时用result二维数组,把path保存起来,并终止本层递归。
所以终止条件代码如下:
if (path.size() == k) {result.push_back(path);return;
}
- 单层搜索的过程
回溯法的搜索过程就是一个树型结构的遍历过程,在如下图中,可以看出for循环用来横向遍历,递归的过程是纵向遍历。

如此我们才遍历完图中的这棵树。
for循环每次从startIndex开始遍历,然后用path保存取到的节点i。
代码如下:
for (int i = startIndex; i <= n; i++) { // 控制树的横向遍历path.push_back(i); // 处理节点 backtracking(n, k, i + 1); // 递归:控制树的纵向遍历,注意下一层搜索要从i+1开始path.pop_back(); // 回溯,撤销处理的节点
}
可以看出backtracking(递归函数)通过不断调用自己一直往深处遍历,总会遇到叶子节点,遇到了叶子节点就要返回。
backtracking的下面部分就是回溯的操作了,撤销本次处理的结果。
关键地方都讲完了,组合问题C++完整代码如下:
class Solution {
private:vector<vector<int>> result; // 存放符合条件结果的集合vector<int> path; // 用来存放符合条件结果void backtracking(int n, int k, int startIndex) {if (path.size() == k) {result.push_back(path);return;}for (int i = startIndex; i <= n; i++) {path.push_back(i); // 处理节点 backtracking(n, k, i + 1); // 递归path.pop_back(); // 回溯,撤销处理的节点}}
public:vector<vector<int>> combine(int n, int k) {result.clear(); // 可以不写path.clear(); // 可以不写backtracking(n, k, 1);return result;}
};
还记得我们在关于回溯算法,你该了解这些! (opens new window)中给出的回溯法模板么?
如下:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}
对比一下本题的代码,是不是发现有点像! 所以有了这个模板,就有解题的大体方向,不至于毫无头绪。
698.划分k个相等的子集
本题的回溯法可以参考这篇文章:
经典回溯算法:集合划分问题「重要更新 🔥🔥🔥」 - 划分为k个相等的子集 - 力扣(LeetCode)
代码:
以前回溯时,我们只需要一个sum即可,比如上面那题分为两个等和子集,实际上只需要考虑一个即可。但是本题有k个,所以我们可以设置k个桶,然后每次dfs时使用一个球,将其放到1~k个桶里面。
对于本题不能使用全局变量findFlag的形式,因为我们一旦找到,即可停止搜索:
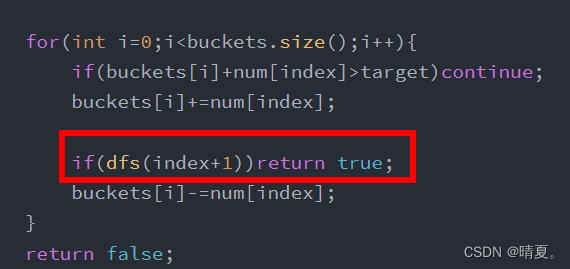
此外这里还有三个剪枝的方法,具体可以看上面那篇文章讲的很详细。
class Solution {
public:int sum=0;int target;int len;vector<int> num;vector<int> buckets;bool canPartitionKSubsets(vector<int>& nums, int k) {num=nums;len=nums.size();for(auto val:nums)sum+=val;if(sum%k!=0)return false;buckets.resize(k);target=sum/k;return dfs(0);}bool dfs(int index){if(index==len){for(int i=0;i<buckets.size();i++){if(buckets[i]!=target)return false;}return true;}for(int i=0;i<buckets.size();i++){if(buckets[i]+num[index]>target)continue;buckets[i]+=num[index];if(dfs(index+1))return true;buckets[i]-=num[index];}return false;}};相关文章:

回溯法——力扣题型全解【更新中】
(本文源自网上教程的笔记) 回溯基础理论 回溯搜索法,它是一种搜索的方式。 回溯是递归的副产品,只要有递归就会有回溯。 所以以下讲解中,回溯函数也就是递归函数,指的都是一个函数。 回溯法的效率 虽然…...

【华为机试真题详解 Python实现】分奖金【2023 Q1 | 100分】
文章目录 前言题目描述输入描述输出描述示例 1题目解析参考代码前言 《华为机试真题详解》专栏含牛客网华为专栏、华为面经试题、华为OD机试真题。 如果您在准备华为的面试,期间有想了解的可以私信我,我会尽可能帮您解答,也可以给您一些建议! 本文解法非最优解(即非性能…...

netlink进行网卡重命名
#include <stdio.h> #include <stdlib.h> #include <string.h> #include <errno.h> #include <unistd.h> #include <sys/socket.h> #include <linux/if.h> #include <linux/netlink.h>#define MAX_PAYLOAD 1024 // 最大负载长…...
-1:针对COVID-19,使用聚类方法有效提取生物特性关联进而识别预防COVID-19的药物)
2023年春【数据分析与挖掘】文献精读(一)-1:针对COVID-19,使用聚类方法有效提取生物特性关联进而识别预防COVID-19的药物
分享给大家——动漫《画江湖之不良人》第四季片尾,主人公 李星云所说的一段话: 悠悠众生,因果循环,大道至简,世间若尽是不如意事, 越是执着,便越是苦,不如安下心来,看该看的风景,做好该做之事。 初行娆疆,所悟如此, 就像曾经有一位紫衣姑娘,第一次来中原时,一样…...
用法)
【Go自学第三节】Go的范围(Range)用法
Go 语言中 range 关键字用于 for 循环中迭代数组(array)、切片(slice)、通道(channel)或集合(map)的元素。在数组和切片中它返回元素的索引和索引对应的值,在集合中返回 key-value 对。 在讲Go语言的range之前,我们先回顾下Python中range的用法 for i …...
【备战面试】每日10道面试题打卡-Day6
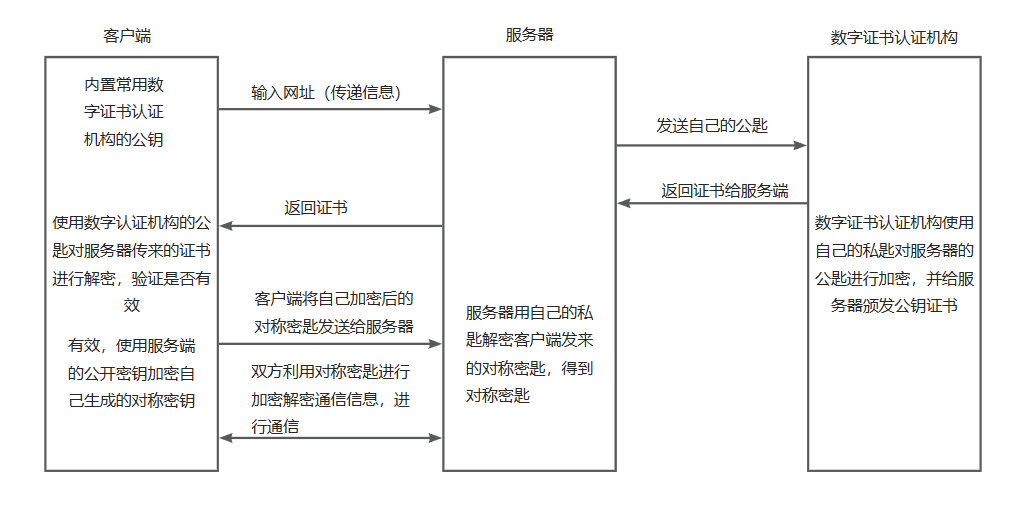
本篇总结的是计算机网络知识相关的面试题,后续也会更新其他相关内容 文章目录1、HTTP 与 HTTPS 有哪些区别?2、HTTPS的加密过程是什么?3、GET与POST有什么区别?4、讲讲HTTP各个版本的区别?5、HTTP与FTP的区别ÿ…...

Stable Diffusion 个人推荐的各种模型及设置参数、扩展应用等合集(不断更新中)
一、说明 | 表示或者 表示 以上 二、模型 适用风景、房子、车子等漫画类风格 模型的VAE不要用模型附带的,好像就是naifu的官方vae,很老了,用 vae-ft-mse-840000-ema-pruned.ckpt 或者是 kl-f8-anime2.ckpt; 嵌入模型要下载作者…...

Salesforce 2023财年逆风增长,现金流达历史最高!
在过去的一年里,Salesforce一直是华尔街最关注的公司之一。3月1日,CRM领域的全球领导者Salesforce公布了截至2023年1月31日的第四季度和整个财年的业绩。 Salesforce主席兼首席执行官Marc Benioff表示: Salesforce全年实现了314亿美元的收入…...

2023年3月全国数据治理工程师认证DAMA-CDGA/CDGP考试怎么通过?
弘博创新是DAMA中国授权的数据治理人才培养基地,贴合市场需求定制教学体系,采用行业资深名师授课,理论与实践案例相结合,快速全面提升个人/企业数据治理专业知识与实践经验,通过考试还能获得数据专业领域证书。 DAMA认…...
【安卓软件】KMPlayer-一款完美的媒体播放器 可以播放所有格式的字幕和视频
KM PlayerKM Player是一款未编码的视频播放器,让您无需编码即可方便地播放各种格式的视频,并为您的新体验添加了字幕支持、视频播放速度和手势等功能。KMPlayer 拥有美观和直观的设计,让您可以更方便地管理和播放视频!功能高品质视…...

ClickHouse--分布式查询多副本的路由规则
前言在集群情况下,数据写入可以有写本地表和写分布式表2种方案,但是面向集群查询时,只能通过Distributed表引擎实现。本文主要介绍分布式查询多副本的路由规则。该配置项为:load_balancerandom/nearest_hostname/in_order/first_o…...

Linux 常用命令总结
本篇博客记录读研以来高频使用的 linux 系统下的命令合集 命令分类程序运行系统相关文件处理文件传输相关命令文件显示相关命令文件排列相关命令Anaconda 相关命令tmux 终端复用神器使用tips程序运行 自动保存日志,替代write命令: xxx | tee ./xxx.log…...

超分扩散模型 SR3 可以做图像去雨、去雾等恢复任务吗?
文章目录前言代码及原文链接主要的点如何进行图像恢复前言 关于扩散模型以及条件扩散模型的介绍,大家可以前往我的上一篇博客:扩散模型diffusion model用于图像恢复任务详细原理 (去雨,去雾等皆可),附实现代码。 SR3是利用扩散模…...

STM32Cube STM32MP157 M4端CAN通讯实战
1、环境 开发系列:STM32MP157 开发软件:STM32CubeIDE 1.4.0 例程目的:在M4端实现CAN通讯 2、目的 近日,有客户需要在STM32MP157中的M4端实现CAN通讯,我也是初次在M4端编写CAN通讯代码,上网研究了其他人写…...

npm install报错unable to resolve dependency tree
一、问题背景npm install安装项目依赖时报错PS D:\test> npm install npm ERR! code ERESOLVE npm ERR! ERESOLVE unable to resolve dependency tree npm ERR! npm ERR! While resolving: vue-admin-template4.2.1 npm ERR! Found: webpack5.74.0 npm ERR! node_modules/we…...

力扣sql简单篇练习(二十六)
力扣sql简单篇练习(二十六) 1 每家商店的产品价格 1.1 题目内容 1.1.1 基本题目信息 1.1.2 示例输入输出 1.2 示例sql语句 # 多行变成多列,考虑用sum if分组 SELECT product_id,sum(IF(storestore1,price,null)) store1,sum(IF(storestore2,price,null)) store2, sum(IF(st…...
网络安全竞赛试题A模块第九套解析(详细))
2022年全国职业院校技能大赛(中职组)网络安全竞赛试题A模块第九套解析(详细)
2022年全国职业院校技能大赛(中职组) 网络安全竞赛试题 (9) (总分100分) 赛题说明 一、竞赛项目简介 “网络安全”竞赛共分A.基础设施设置与安全加固;B.网络安全事件响应、数字取证调查和应用安全;C.CTF夺旗-攻击;D.CTF夺旗-防御等四个模块。根据比赛实际情况,竞…...

C++回顾(十六)—— 异常处理机制
16.1 异常的基本语法 1) 若有异常则通过throw操作创建一个异常对象并抛掷。2) 将可能抛出异常的程序段嵌在try块之中。控制通过正常的顺序执行到达try语句,然后执行try块内的保护段。3) 如果在保护段执行期间没有引起异常…...

【100个 Unity实用技能】 | Unity 在代码中 动态改变RectTransform位置及宽高 的方法整理
Unity 小科普 老规矩,先介绍一下 Unity 的科普小知识: Unity是 实时3D互动内容创作和运营平台 。包括游戏开发、美术、建筑、汽车设计、影视在内的所有创作者,借助 Unity 将创意变成现实。Unity 平台提供一整套完善的软件解决方案ÿ…...
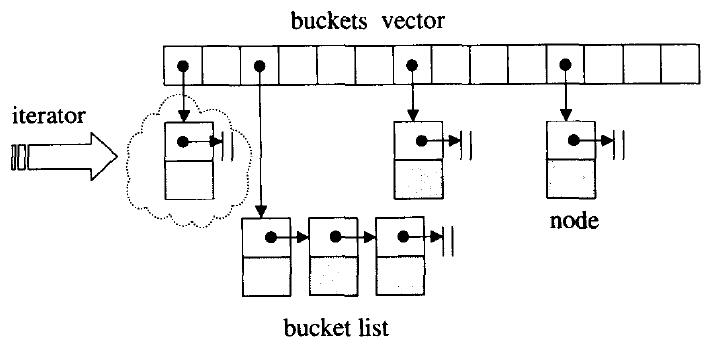
哈希表的实现
哈希表概念 二叉搜索树具有对数时间的表现,但这样的表现建立在一个假设上:输入的数据有足够的随机性。哈希表又名散列表,在插入、删除、搜索等操作上具有「常数平均时间」的表现,而且这种表现是以统计为基础,不需依赖…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
