数据结构【队列】
队列的的概念
队列是一种特殊的线性表,特殊之处在于它只允许在表的头部进行删除操作,而在表的尾部进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。队列中没有元素时,称为空队列。
队列的特点
- 先进先出:这是队列最大的特点,队列中所有的元素都遵循先进先出的原则进行管理数据,最先入队列的一定会最先出队列。
- 受限访问:队列操作数据时,只能对队头或者队尾进行操作。入队(插入数据)只会在队尾进行,出队(删除数据)只会在对头进行。
- 高效:进行删除和插入数据,最坏情况下的时间复杂度是O(1)。
队列的接口实现
队列可以使用数组和链表来实现,但是链表实现起来更清晰。
队列的结构
typedef int QUEDATATYPE;typedef struct QueueNode
{QUEDATATYPE data;struct QueueNode* next;
}QUENODE;
但是这样有个问题,我每次插入都要找尾节点,这样就太慢了,所以我们就用两个指针来解决这个问题,一个指针指向队列的头节点,一个用来指向队列的尾节点。
typedef int QUEDATATYPE;typedef struct QueueNode
{QUEDATATYPE data;struct QueueNode* next;
}QUENODE;typedef struct Queue
{QUENODE* phead;QUENODE* ptail;int size;
}Queue;
队列的初始化
//初始化队列
void QueueInit(Queue* pq)
{assert(pq);pq->phead = pq->ptail = NULL;pq->size = 0;
}
入队
入队操作在尾部进行
这里有有两个情况,队列为空与非空。
- 为空的话,就直接将新节点赋给
phead和ptail。 - 非空,将
ptail的next指针指向新节点,再更新ptail。
//入队
void QueuePush(Queue* pq, QUEDATATYPE x)
{assert(pq);if (pq->phead == NULL){QUENODE* Node = (QUENODE*)malloc(sizeof(QUENODE));if (Node == NULL){perror("malloc fail");exit(1);}Node->data = x;Node->next = NULL;pq->phead = pq->ptail = Node;}else{QUENODE* Node = (QUENODE*)malloc(sizeof(QUENODE));if (Node == NULL){perror("malloc fail");exit(1);}Node->data = x;Node->next = NULL;pq->ptail->next = Node;pq->ptail = Node;}pq->size++;
}
出队
出队操作在队头进行
出队同样也有两种情况,只剩下一个节点和多个节点。
- 只有一个节点:也就是只有头节点了,直接将头节点释放掉就好了。
- 多个节点:将头节点释放,更新头节点
//出队
void QueuePop(Queue* pq)
{assert(pq && pq->size > 0);if (pq->phead->next == NULL){free(pq->phead);pq->phead = pq->ptail = NULL;}else{QUENODE* tmp = pq->phead;pq->phead = pq->phead->next;free(tmp);tmp = NULL;}pq->size--;
}
获取队头元素
// 获取队头元素
QUEDATATYPE QueueHead(Queue* pq)
{assert(pq);return pq->phead->data;
}
判空
//判空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->size == 0;
}
获取栈中有效元素个数
// 获取栈中有效元素个数
int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}
销毁队列
//销毁队列
void QueueDestroy(Queue* pq)
{QUENODE* tmp = pq->phead;while (tmp){pq->phead = pq->phead->next;free(tmp);tmp = pq->phead;}pq->phead = pq->ptail = NULL;pq->size = 0;
}
完整代码
Queue.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>typedef int QUEDATATYPE;typedef struct QueueNode
{QUEDATATYPE data;struct QueueNode* next;
}QUENODE;typedef struct Queue
{QUENODE* phead;QUENODE* ptail;int size;
}Queue;//初始化队列
void QueueInit(Queue* pq);
//入队
void QueuePush(Queue* pq, QUEDATATYPE x);
//出队
void QueuePop(Queue* pq);
// 获取队头元素
QUEDATATYPE QueueHead(Queue* pq);
//判空
bool QueueEmpty(Queue* pq);
// 获取栈中有效元素个数
int QueueSize(Queue* pq);
//销毁队列
void QueueDestroy(Queue* pq);
Queue.c
#include"Queue.h"//初始化队列
void QueueInit(Queue* pq)
{assert(pq);pq->phead = pq->ptail = NULL;pq->size = 0;
}//入队
void QueuePush(Queue* pq, QUEDATATYPE x)
{assert(pq);if (pq->phead == NULL){QUENODE* Node = (QUENODE*)malloc(sizeof(QUENODE));if (Node == NULL){perror("malloc fail");exit(1);}Node->data = x;Node->next = NULL;pq->phead = pq->ptail = Node;}else{QUENODE* Node = (QUENODE*)malloc(sizeof(QUENODE));if (Node == NULL){perror("malloc fail");exit(1);}Node->data = x;Node->next = NULL;pq->ptail->next = Node;pq->ptail = Node;}pq->size++;
}//出队
void QueuePop(Queue* pq)
{assert(pq && pq->size > 0);if (pq->phead->next == NULL){free(pq->phead);pq->phead = pq->ptail = NULL;}else{QUENODE* tmp = pq->phead;pq->phead = pq->phead->next;free(tmp);tmp = NULL;}pq->size--;
}// 获取队头元素
QUEDATATYPE QueueHead(Queue* pq)
{assert(pq);return pq->phead->data;
}//判空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->size == 0;
}// 获取栈中有效元素个数
int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}//销毁队列
void QueueDestroy(Queue* pq)
{QUENODE* tmp = pq->phead;while (tmp){pq->phead = pq->phead->next;free(tmp);tmp = pq->phead;}pq->phead = pq->ptail = NULL;pq->size = 0;
}
结语
最后感谢您能阅读完此片文章,如果有任何建议或纠正欢迎在评论区留言,也可以前往我的主页看更多好文哦(点击此处跳转到主页)。
如果您认为这篇文章对您有所收获,点一个小小的赞就是我创作的巨大动力,谢谢!!!
相关文章:

数据结构【队列】
队列的的概念 队列是一种特殊的线性表,特殊之处在于它只允许在表的头部进行删除操作,而在表的尾部进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。队列中…...
微信小程序上架,AI类目审核(AI问答、AI绘画、AI换脸)
小程序对于生成式AI类目的产品上架审核较为严格,这也是近两年新增了几个类目,一旦小程序中涉及生成式AI相关的内容,如果你选择相应类目,但审核被划归为这一类,都需要准备此类目的审核,才能正常上架。 如果…...

Vue3学习记录(第一天)
Vue3学习记录_第一天 背景说明记录Vue3实现响应式前端的反射前端对象的属性赋值Vue3响应式实现过程稿前端移除对象的属性 背景 本次学习主要是看视频学习, 没有跟练, 但是很多知识点感觉又容易忘记. 所以通过笔记的方式输出一下. 说明 估计只能自己看懂, 如果能提供一些其他…...
springboot+vue+mybatis房屋租贷系统+PPT+论文+讲解+售后
本论文系统地描绘了整个网上房屋租赁系统的设计与实现,主要实现的功能有以下几点:管理员;首页、个人中心、房屋类型管理、房屋租赁管理、会员管理、订单信息管理、合同信息管理、退房评价管理、管理员管理,系统管理,前…...
Day30 登录界面设计
本章节,实现了登录界面窗口设计 一.准备登录界面图片素材(透明背景图片) 把准备好的图片放在 Images 文件夹下面,格式分别是 .png和 .icoico 图片,右键属性,生成操作选 内容 png 图片,右键属性,生成操作选 资源 选中 login.png图片鼠标右键,选择属性。生成的操作选…...

VOJ 迷阵突围 题解 次短路径 dijkstra算法
迷阵突围 题目描述 小明陷入了坐标系上的一个迷阵,迷阵上有 n 个点,编号从 1 到 n 。小明在编号为 1 的位置,他想到编号为 n 的位置上。小明当然想尽快到达目的地,但是他觉得最短的路径可能有风险,所以他会选择第二短…...

Oracle SQL详解
Oracle SQL是一种用于管理和操作Oracle数据库的编程语言。以下是一些基本的Oracle SQL语法和建表建用户的详解。 创建用户 在Oracle中,创建用户通常需要具有足够权限的用户(通常是具有DBA角色的用户)。以下是一个创建用户的例子:…...

产业,到底需要什么大模型?
[ 产业究竟需要怎样的大模型?关于这个问题,本文作者便提出了他的看法,并总结了产业大模型目前阶段的三点落地挑战。一起来看看,或许可以帮助你更好地理解大模型与行业、与产业的融合。 写下这篇的起因,是前不久的一件事…...
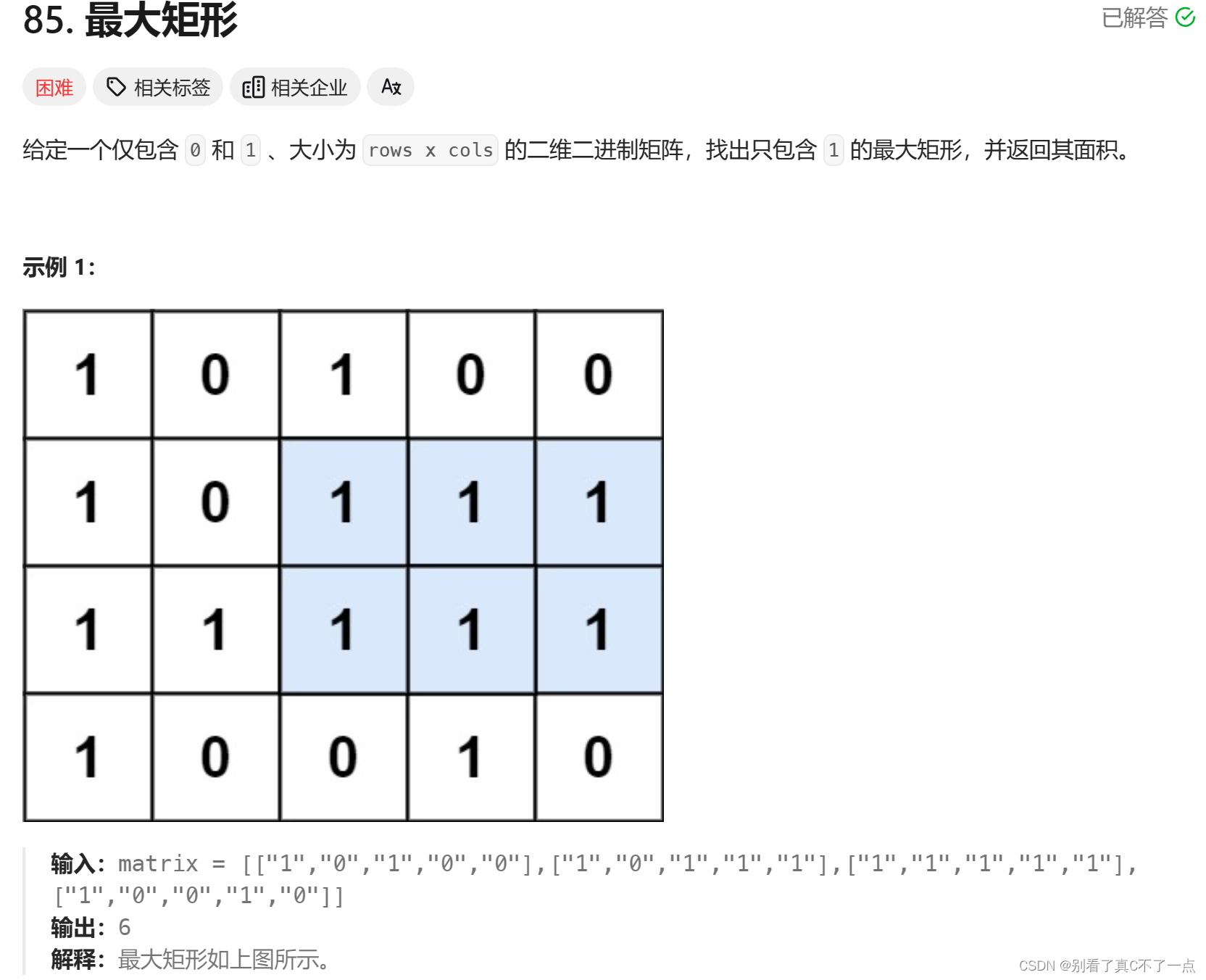
每日5题Day17 - LeetCode 81 - 85
每一步向前都是向自己的梦想更近一步,坚持不懈,勇往直前! 第一题:81. 搜索旋转排序数组 II - 力扣(LeetCode) class Solution {public boolean search(int[] nums, int target) {int n nums.length;if (n…...

后端开发面经系列 --中望C++面经
中望C面经,全部内容! 公众号:阿Q技术站 文章目录 中望C面经,全部内容!一面 8.15 时长45min1、介绍项目相关2、gdb怎么调试的?打断点用什么指令?3、gcc的编译过程4、cmake添加头文件搜索路径用…...
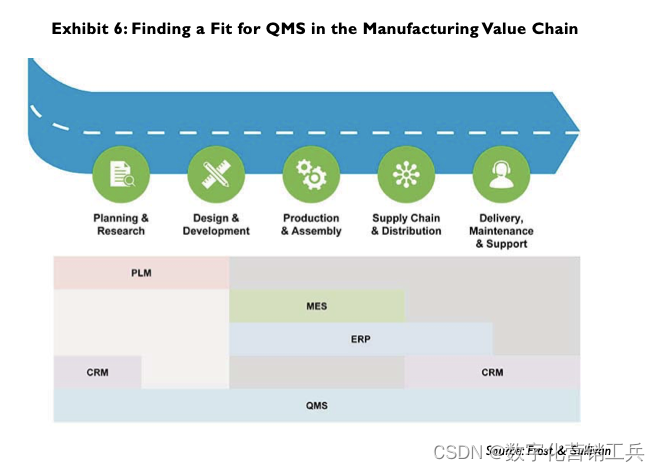
德国西门子论未来质量管理 - 如何与明天相遇?
未来制造业的质量 -- 如何用软件方案满足质量要求 作者:Bill Butcher 翻译&编辑:数字化营销工兵 【前言】在Frost&Sullivan最近发表的一份白皮书中,他们讨论了制造业的质量投资。质量是制造过程的关键要素,但似乎比其他…...
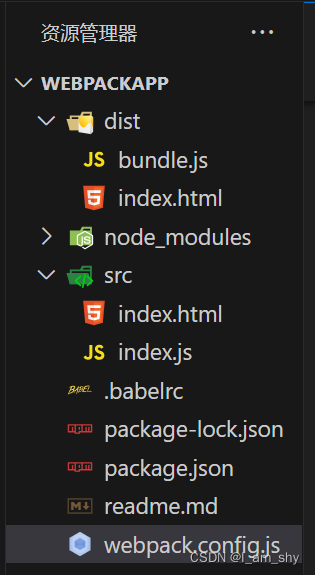
webpack快速入门---webpack的安装和基本使用
webpack是什么 本质上,webpack 是一个用于现代 JavaScript 应用程序的 静态模块打包工具。当 webpack 处理应用程序时,它会在内部从一个或多个入口点构建一个 依赖图(dependency graph),然后将你项目中所需的每一个模块组合成一个或多个 bund…...

后端开发面经系列 -- 华为C++一面面经
HUAWEI – C一面面经 公众号:阿Q技术站 来源:https://www.nowcoder.com/feed/main/detail/b8113ff340d7444985b32a73c207c826 1、计网的协议分几层?分别叫什么? OSI七层模型 物理层 (Physical Layer): 负责物理设备之间的原始比…...
csrf漏洞与ssrf漏洞
环境:用kali搭建的pikachu靶场 一.CSRF 1.CSRF漏洞简介 跨站请求伪造(CSRF)漏洞是一种Web应用程序安全漏洞,攻击者通过伪装成受信任用户的请求来执行未经授权的操作。这可能导致用户在不知情的情况下执行某些敏感操作࿰…...
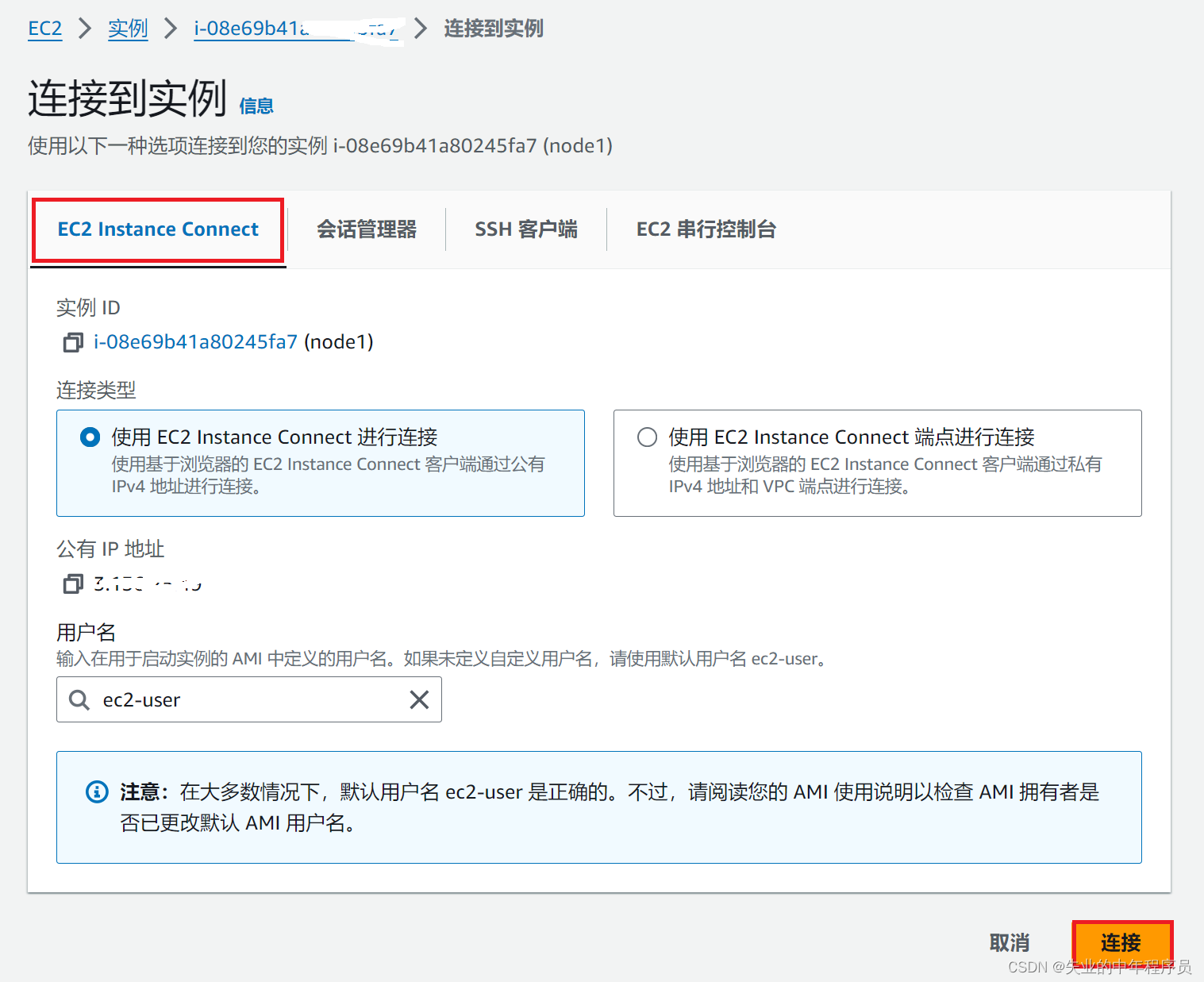
AWS EC2服务器开启root密码,SSH登录
1) EC2 Instance Connect连接,更改root密码 sudo passwd root 2)接着切换到切换到 root 身份,编辑 SSH 配置文件 $ sudo -i$ vi /etc/ssh/sshd_configPasswordAuthentication no,把 no 改成 yes #PermitRootLogin prohibit-passw…...

常见代码版本管理工具
目录 一、引言 二、Gitee (一)优点与特点 (二)缺点 (三)使用报告 三、GitHub 四、SVN 五、总结 一、引言 在软件开发过程中,代码版本控制工具是不可或缺的。Gitee、GitHub和SVN是三种常…...
最新版点微同城源码34.7+全套插件+小程序前后端
带全套插件 自己耐心点配置一下插件 可以H5可以小程序 一款专属的同城服务平台对于企业和个人而言,无疑是拓展业务、提升服务品质的重要一环。点微同城源码搭配全套插件,以及完善的小程序前后端,将为您的业务发展提供强大支持 源码免费下载…...
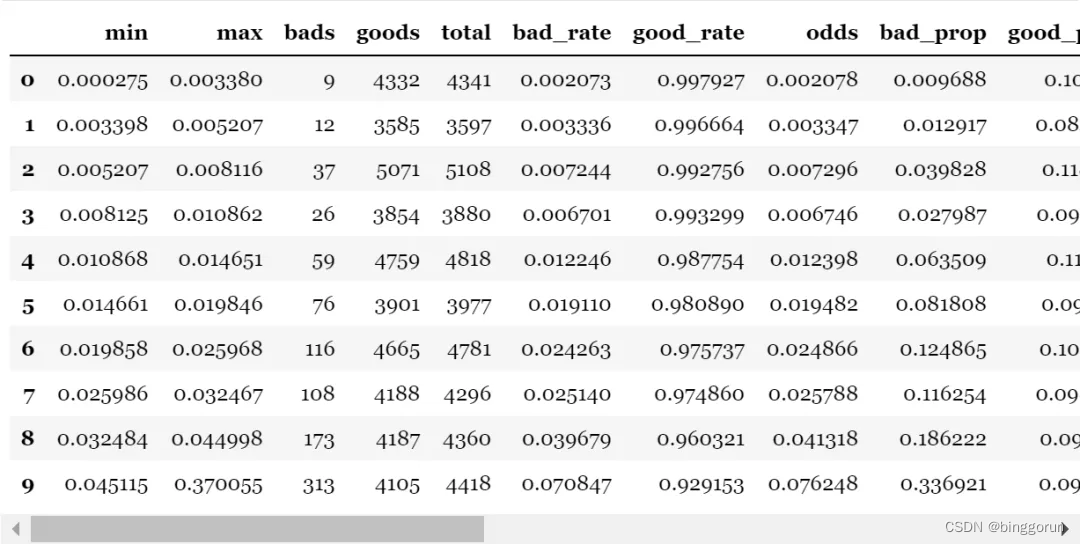
逻辑回归及python实现
概述 logistic回归是一种广义线性回归(generalized linear model),因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同,都具有 w‘xb,其中w和b是待求参数,其区别在于他们的因变量不同&#x…...

大模型押题高考语文作文,带着大模型参加语文高考会怎么样?
前沿 大语言模型通常是指那些经过大量数据训练,能够理解和生成自然语言文本的人工智能系统。这些模型通常具有数百万到数十亿个参数,能够执行多种语言任务,例如语言翻译、文本摘要、问答系统、文本生成等。大语言模型能够捕捉语言的复杂性和细微差别,提供更加准确和自然的…...
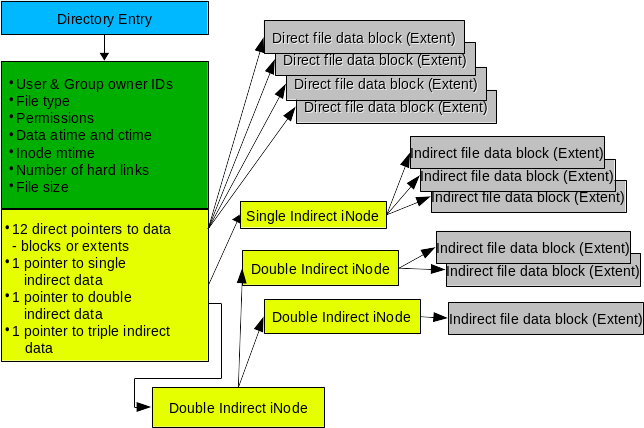
Linux Ext2/3/4文件系统
文章目录 前言一、Linux文件系统简介1.1 简介1.2 Linux File System Structure1.3 Directory Structure 二、Ext2/3/4文件系统2.1 Minix2.2 EXT2.3 EXT22.4 EXT32.5 EXT4 三、EXT Inode参考资料 前言 这篇文章介绍了Linux文件系统的一些基础知识:Linux 文件系统简介…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
