spark MLlib 中的分类模型
理解这些机器学习模型的数学原理需要一定的数学基础,下面我将简要介绍每个模型的数学原理,并附上相关的数学公式。
1. LinearSVC(线性支持向量机)
数学原理: 线性支持向量机的目标是找到一个超平面,最大化训练数据集中样本点到超平面的间隔,并且使得间隔内没有样本点。其决策函数为:
[
f(x) = \text{sign}(\mathbf{w}^T \mathbf{x} + b)
]
其中,(\mathbf{w}) 是法向量,(b) 是截距。
算法: LinearSVC 使用 Hinge Loss 作为损失函数,并采用 OWLQN(Orthant-Wise Limited-memory Quasi-Newton)算法进行求解。
2. LogisticRegression(逻辑回归)
数学原理: 逻辑回归是一种广义线性模型,其输出通过 logistic 函数进行映射,表示样本属于某个类别的概率。其假设函数为:
[
h_{\mathbf{w}}(\mathbf{x}) = \frac{1}{1 + e{-\mathbf{w}T \mathbf{x}}}
]
算法: 逻辑回归通过最小化交叉熵损失函数来拟合模型参数。常用的优化算法有梯度下降和拟牛顿法(如 LBFGS)。
3. DecisionTreeClassifier(决策树分类器)
数学原理: 决策树通过对特征进行划分,构建一棵树来实现对数据集的分类。其基本算法如下:
- 选择最优的特征进行节点划分。
- 递归地对每个子节点重复步骤 1,直到满足终止条件(如节点包含的样本数小于某个阈值)。
算法: 决策树分类器通常使用信息增益或基尼不纯度等指标来选择最优的特征进行节点划分,并通过递归地构建树来进行训练。
4. GBTClassifier(梯度提升树分类器)
数学原理: 梯度提升树是一种集成学习算法,其基本思想是通过迭代地训练多个决策树,并使用梯度下降来最小化损失函数。其预测函数为:
[
F(x) = \sum_{i=1}^{N} f_i(x)
]
其中,(f_i(x)) 是第 (i) 个决策树的输出。
算法: GBTClassifier 通过梯度提升算法训练多个决策树,每次迭代时通过梯度下降来拟合一个新的回归树。
5. RandomForestClassifier(随机森林分类器)
数学原理: 随机森林是一种集成学习算法,其基本思想是通过训练多个决策树,并通过投票或平均值来确定最终的分类结果。其预测函数为:
[
F(x) = \text{mode}(f_1(x), f_2(x), …, f_N(x))
]
其中,(f_i(x)) 是第 (i) 个决策树的输出。
算法: RandomForestClassifier 通过随机选择特征子集和样本子集来构建每棵树,然后使用投票或平均值来确定最终的分类结果。
6. NaiveBayes(朴素贝叶斯分类器)
数学原理: 朴素贝叶斯分类器基于贝叶斯定理和特征条件独立性假设。其分类概率计算公式为:
[
P(Y|X) = \frac{P(X|Y)P(Y)}{P(X)}
]
其中,(P(Y|X)) 是在给定特征 (X) 的条件下类别 (Y) 的后验概率。
算法: NaiveBayes 通过计算每个类别的先验概率和每个特征的条件概率来进行分类。
7. MultilayerPerceptronClassifier(多层感知机分类器)
数学原理: 多层感知机分类器是一种基于神经网络的分类模型,其基本原理是通过多层神经元对特征进行非线性组合和映射。其前向传播公式为:
[
z^{(l+1)} = w^{(l)} a^{(l)} + b^{(l)}
]
[
a^{(l+1)} = \sigma(z^{(l+1)})
]
其中,(w^{(l)}) 和 (b^{(l)}) 分别是第 (l) 层的权重和偏置,(\sigma) 是激活函数。
算法: MultilayerPerceptronClassifier 通过反向传播算法来训练多层神经网络,并通过梯度下降来最小化损失函数。
相关文章:

spark MLlib 中的分类模型
理解这些机器学习模型的数学原理需要一定的数学基础,下面我将简要介绍每个模型的数学原理,并附上相关的数学公式。 1. LinearSVC(线性支持向量机) 数学原理: 线性支持向量机的目标是找到一个超平面,最大化…...

24上半年报考人数“不增反降”?备考下半年软考的难了......
近日,工信教考发布了一篇《2024年上半年计算机软件资格考试顺利举行》的文章,公布了2024年上半年软考报考人数共计52.77万人,其中,初级资格5.12万人、中级资格24.37万人、高级资格23.28万人。 软考高级占总报名人数的44%…...
初出茅庐的小李博客之使用立创开发板(ESP32)连接到EMQX Platform【MQTT TLS/SSL 端口连接】
介绍 手上有一块立创开发板,本着不吃灰的原则把它用起来,今天就来用它来连接上自己部署的MQTT服务器进行数据通信。 硬件:立创开发板 开发环境:Arduino IDE Win11 MQTT 平台:EMQX Platform 立创开发板介绍࿱…...

js平滑滚动元素使其可见
直接上重点: let xpath "//*/div[idxxx]"; document.evaluate(xpath, document, null, XPathResult.FIRST_ORDERED_NODE_TYPE, null).singleNodeValue.scrollIntoView({ behavior: "smooth"})这段代码是JavaScript中使用XPath查询文档并执行平…...

TP6 事件绑定、监听、订阅
事件绑定与监听 命令行生成事件类 php think make:event EventDemo 命令行生成事件监听类php think make:listener ListenerDemo 事件类可作为保存与事件相关信息的容器,如没有额外需求可以不需要定义 事件系统的所有操作都通过think\facade\Event类进行静态调用 当定义…...

SpringCloud Gateway中Filters详细说明
前面 https://blog.csdn.net/J080624/article/details/139494909 我们研究了GateWay中各种路由断言的使用。SpringCloud GateWay 还提供了各种过滤器用来对请求和响应进行处理。 官网地址:SpringCloud Gateway Filter 【1】GatewayFilter Factories 路由过滤器允…...

力扣2156.查找给定哈希值的子串
力扣2156.查找给定哈希值的子串 rolling hash:求带权的值 左边是高位 右边是低位 本题要求左边低位 只要反向求即可 class Solution {public:string subStrHash(string s, int power, int modulo, int k, int hashValue) {int n s.size();long long M modulo,p…...
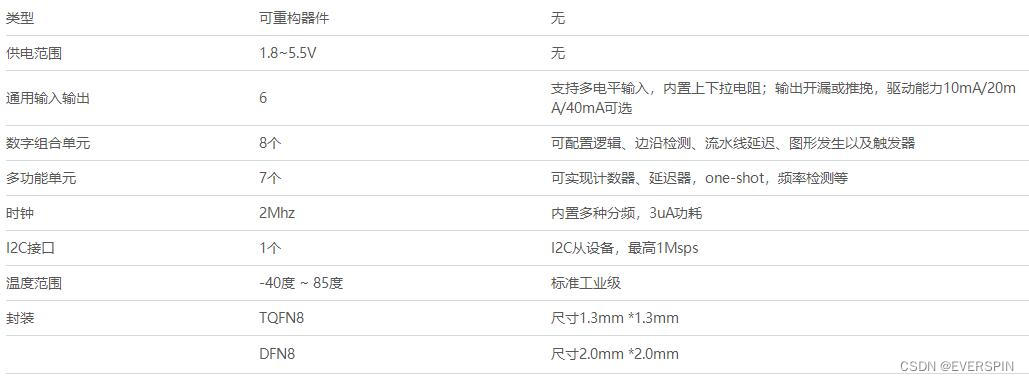
推荐低成本低功耗的纯数字现场可重构IC
CPLD采用CMOS EPROM、EEPROM、快闪存储器和SRAM等编程技术,从而构成了高密度、高速度和低功耗的可编程逻辑器件。 RAMSUN提供的型号LS98003是通用可配置的数字逻辑芯片,有体积小、超低功耗和高可靠性等特点。客户可以根据自己的功能需求设计芯片&#x…...

解决change事件与blur事件互不影响
<template><div style"margin-top: 40px"><el-selectv-model"form.name"placeholder"请选择名称"clearablefilterableref"selectName"allow-createblur"nameBlur($event)"visible-change"visibleNameCh…...

后端开发面经系列 -- 同程旅行C++一面
同程旅行C一面 公众号:阿Q技术站 文章目录 同程旅行C一面1、sizeof与strlen的区别?2、运算符和函数有什么区别?3、new和malloc?4、内存泄漏与规避方法?5、悬空指针与野指针?6、手撕冒泡排序?7、…...

推荐几个开源的c#的工作流引擎组件
以下是一个.NET Core领域可以推荐使用的流程引擎的表格: 名称 生产厂家 下载地址 支持二开 独立部署 ccflow 济南驰骋信息技术有限公司 https://gitee.com/opencc 是 是 Elsa Elsa Workflows GitHub - elsa-workflows/elsa-core: A .NET workflows li…...
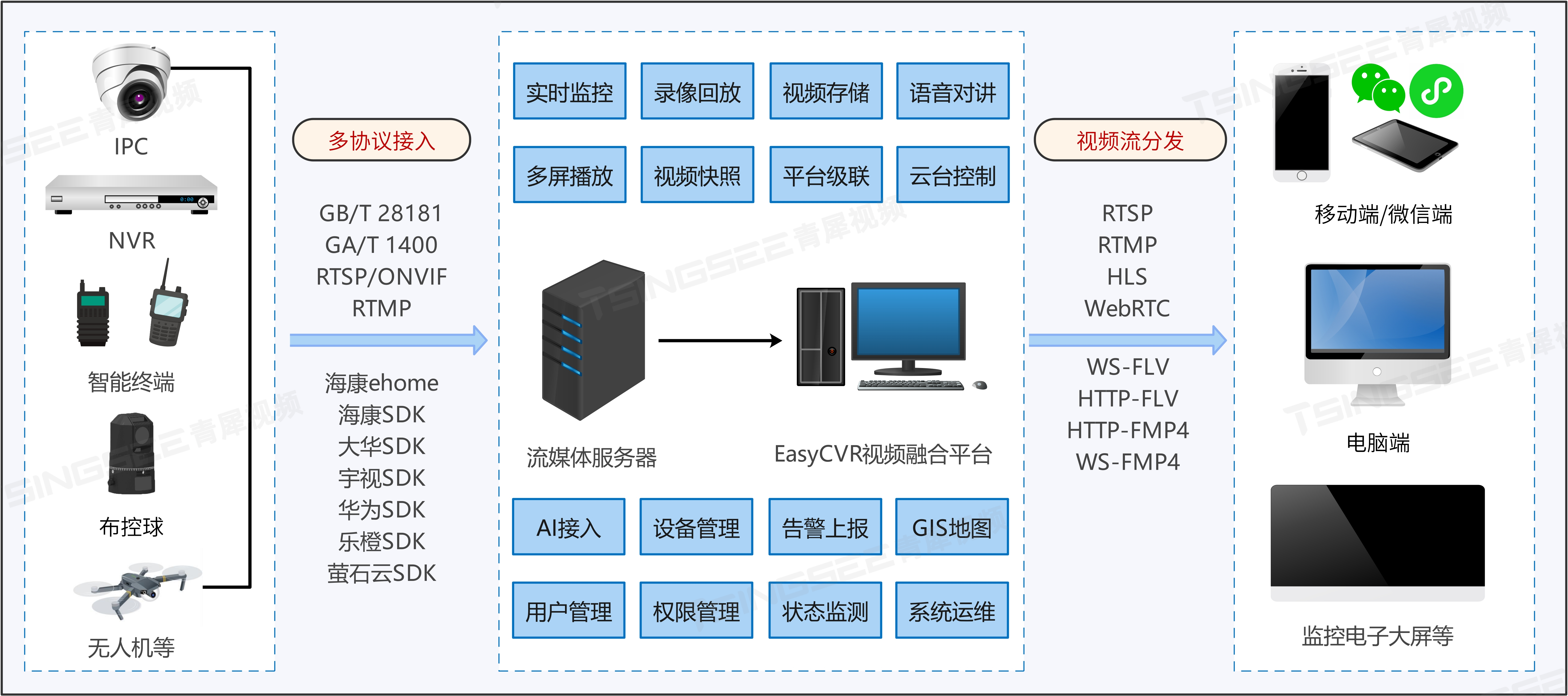
视频汇聚EasyCVR视频监控云平台对接GA/T 1400视图库对象和对象集合XMLSchema描述
GA/T 1400协议主要应用于公安系统的视频图像信息应用系统,如警务综合平台、治安防控系统、交通管理系统等。在城市的治安监控、交通管理、案件侦查等方面,GA/T 1400协议都发挥着重要作用。 以视频汇聚EasyCVR视频监控资源管理平台为例,该平台…...

【JavaScript脚本宇宙】瞬息万变:探索实时Web应用的JavaScript库
鸟瞰实时Web开发:JavaScript库大比拼 前言 随着Web应用程序的发展,实时通讯已成为一个重要的需求。本篇文章将探索六个关键的JavaScript库,这些库为我们提供助力,使得实时Web应用程序的创建成为可能。 欢迎订阅专栏:…...
)
Java数据结构与算法(有向无环图)
前言 有向无环图(Directed Graph)是在有向图的基础上,增加无环的检查。 实现原理 使用邻接表表示法实现有向图相对简单明了,步骤也相对简单。 1:首先创建有向图 2.创建顶点 3.顶点间创建边 4.创建边的过程中检查节点是否存…...

QuanTA: 一种新的高秩高效微调范式
QuanTA方法的核心是利用张量操作来模拟量子电路中的门操作。这些张量被设计为仅在特定的轴上应用,类似于量子电路中的单量子比特或双量子比特门。通过这种方式,QuanTA能够以高秩参数化来适应LLMs的权重矩阵。 网址:QuanTA: 一种新的高秩高效微…...

【漏洞复现】用友NC downCourseWare 任意文件读取漏洞
0x01 产品简介 用友NC是一款企业级ERP软件。作为一种信息化管理工具,用友NC提供了一系列业务管理模块,包括财务会计、采购管理、销售管理、物料管理、生产计划和人力资源管理等,帮助企业实现数字化转型和高效管理。 0x02 漏洞概述 用友NC …...

度安讲 | 第二期「安全左移·业务护航」技术沙龙成功举办
当下,“安全左移”作为落地DevSecOps的重要实践之一,已在业界达成共识。DevSecOps作为一种集开发、安全、运维于一体的软件开发和运营模式,强调在敏捷交付下,“安全”在软件开发生命周期的全覆盖贯穿和核心位置。所谓“安全左移”…...
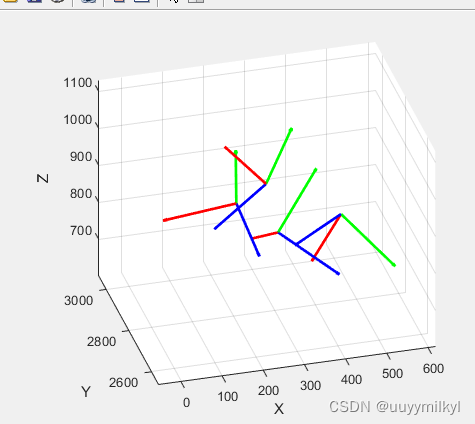
代码片段 | Matlab三维图显示[ R T 0 1] 的最佳方法
% 输入N组RT矩阵 N 4; R zeros(3, 3, N); T zeros(3, N); R(:,:,1) [-0.902608 0.250129 0.350335 ; 0.314198 0.939127 0.138996 ;-0.294242 0.235533 -0.926253 ]; T(:,1) [205.877;2796.02; 907.116];R(:,:,2) [-0.123936 0.643885 0.755018 ;0.816604 0.464468 -0.26…...
2024百度之星 跑步
原题链接:码题集OJ-跑步 题目大意:一个n个人在绕圈跑,第i个人跑一圈的时间是i分钟,每二个人位置相同就会打一次招呼,如果同时来到终点,他们就会停下来,请问会打多少次招呼? 思路&a…...
【git】TortoiseGitPlink Fatal Error 解决方法
背景 使用 TortoiseGit报错: TortoiseGitPlink Fatal Error No supported authentication methods available (server sent: publickey) 解决方法 1、有很多是重置git的秘钥解决的 2、重置ssh工具...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...
