2024百度之星 跑步
原题链接:码题集OJ-跑步
题目大意:一个n个人在绕圈跑,第i个人跑一圈的时间是i分钟,每二个人位置相同就会打一次招呼,如果同时来到终点,他们就会停下来,请问会打多少次招呼?
思路:首先可以想到这n个人会跑他们的最小公倍数的圈数之后停下来。最小公倍数用ores代替,如何求最小公倍数呢?一个数肯定是由一堆质数相乘得到的,所以只要求出1-n中每个质数的最高次幂就可以了,例如说要求1 2 3 4 5 6 7 8 9 10的最小公倍数,那么其实就是求1 1 1 1 5 1 7 8 9 1的最小公倍数,因为8=2*2*2,那么2的这个质数本身就不重要了。p字母为质数,那么这个质数的最高次幂就是。
因为跑的快的不会被跑的慢的人追到,那么可以想到一个必定超时的方案,那就是用二层for来枚举。对于第i个人,他前面的所有人都会被他追到,所有第i个人的贡献就是双重循环枚举就可以了,但是数据范围明显会超时,可以想到在双重枚举的过程中肯定会有很多不必要的计算,一个人可以追前面的人,也可以被后面的人追上,如果是追前面的人,那么
是减数,一共有(n-i)个人可以被追上,如果是被追上那么
就是被减数,一共有(i-1)个人,那么减数减去被减数的数量乘上当前数跑的圈数就是打招呼的数量也就是
。例如说1 2 3,如果双重循环计算,第一个人的贡献是:
,第二个人的贡献是:
,如果单独计算,那么第一个的贡献就是:
,第二个人的贡献就是:
。
那这样题目就很明显了,但是因为数据会很大要取模,所以需要算出从1-n的所有数的逆元。对于1-n的逆元可以线性的求出。
inv数组表示逆元
二边同时mod p
二边同时乘上i的逆元和r的逆元
移项变形
q=p/i,r^-1=(p%i)^-1,因为是mod意义下的计算,所以右边可以加上p*(p%i)^-1.
最终就是inv[i]=(mod-mod/i)*inv[mod%i]%mod.
//冷静,冷静,冷静
//调不出来就重构
#pragma GCC optimize(2)
#pragma GCC optimize("O3")
#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll,ll> pii;
const int N=1e7+10,mod=998244353;
ll inv[N],prime[N],n;
bool vis[N];
ll ksm(ll a,ll b)
{ll ans=1;do{if(b&1)ans*=a;a*=a;b>>=1;a%=mod;ans%=mod;}while(b); return ans;
}
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);inv[1]=1;cin>>n;ll cnt=0,ores=1;for(int i=2;i<=n;i++){inv[i]=(mod-mod/i)*inv[mod%i]%mod;//求每个数的逆元 if(!vis[i])prime[cnt++]=i,ores=ores*ksm(i,log(n)/log(i))%mod;//求n范围内的质数的最高次幂的乘积 for(int j=0;j<cnt&&i*prime[j]<=n;j++){vis[i*prime[j]]=1;if(i%prime[j]==0)break;}}ll ans=0;for(int i=1;i<=n;i++){ll op=ores*inv[i]%mod;//这个人跑的圈数 ans=(ans+op*(n-2*i+1)%mod+mod)%mod; }cout<<ans;return 0;
}
相关文章:
2024百度之星 跑步
原题链接:码题集OJ-跑步 题目大意:一个n个人在绕圈跑,第i个人跑一圈的时间是i分钟,每二个人位置相同就会打一次招呼,如果同时来到终点,他们就会停下来,请问会打多少次招呼? 思路&a…...
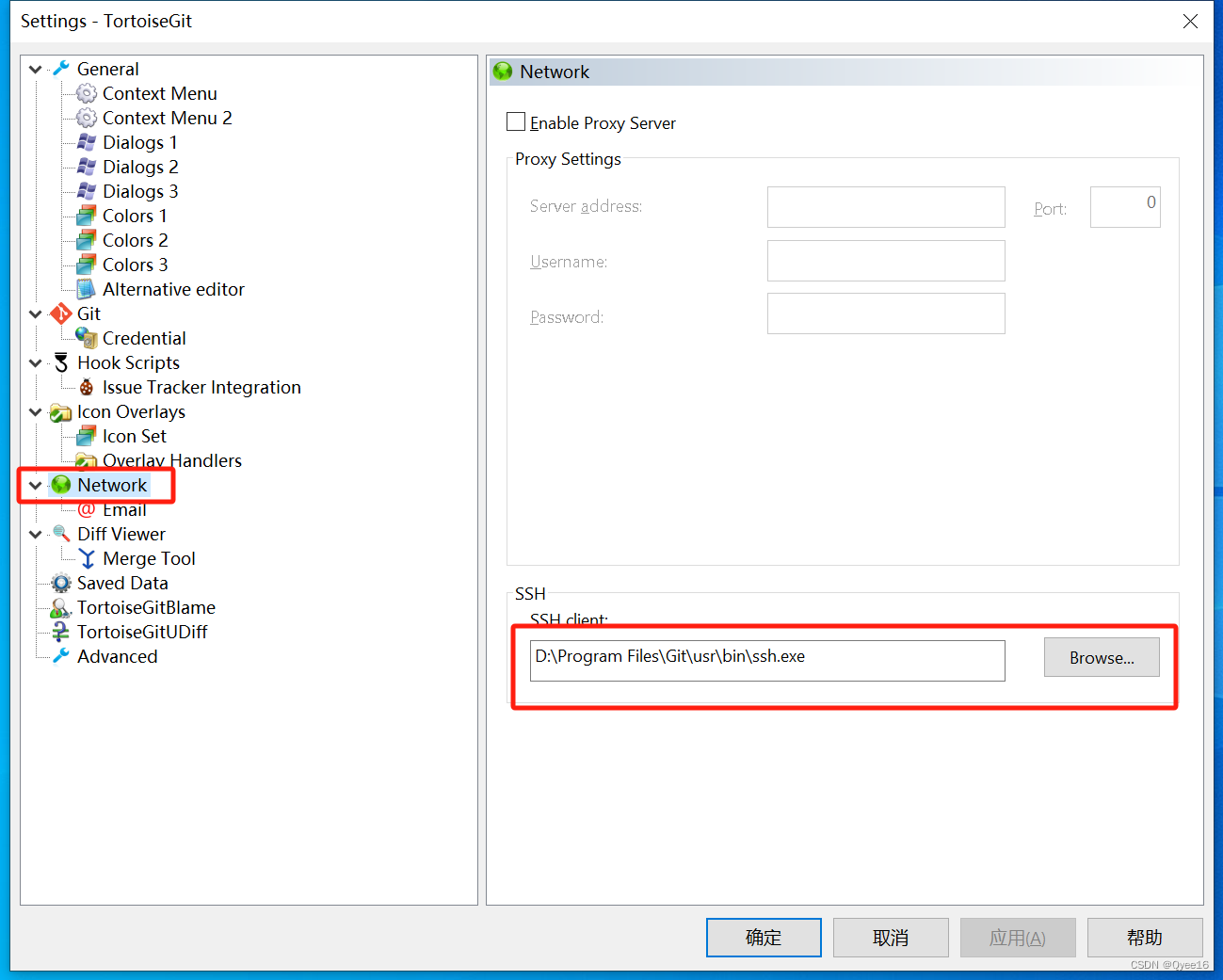
【git】TortoiseGitPlink Fatal Error 解决方法
背景 使用 TortoiseGit报错: TortoiseGitPlink Fatal Error No supported authentication methods available (server sent: publickey) 解决方法 1、有很多是重置git的秘钥解决的 2、重置ssh工具...

行心科技|中科利众:健康科技新合作,营养与科技融合前行
2024中国国际大健康产业文化节暨第34届国际大健康产业交易博览会于2024年5月31日在保利世贸博览馆盛大开幕,行心科技与中科利众(贵州)生物科技有限公司不谋而合,就“膳食机能健康问题解决方案”达成战略合作,共同开启膳…...
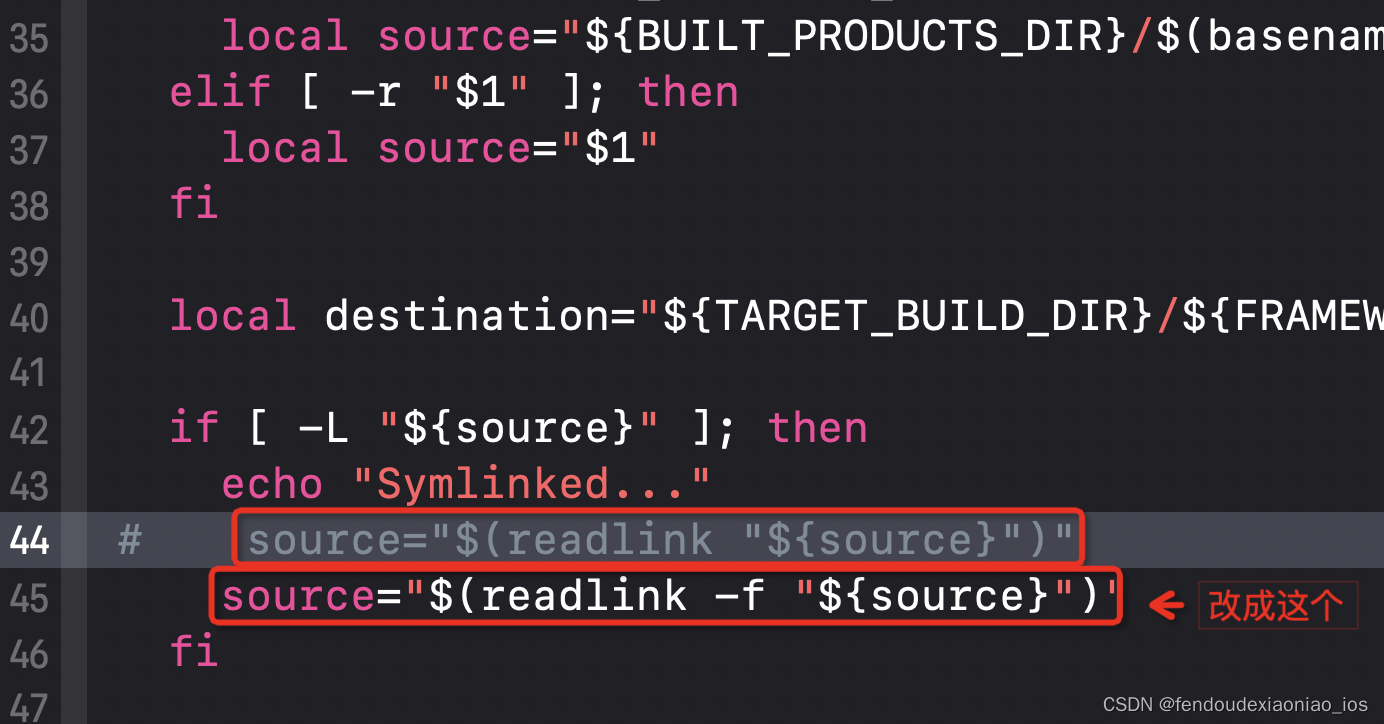
Xcode 打包报错Command PhaseScriptExecution failed with a nonzero exit code
解决办法: 1、在Xcode项目中 Pods -> Targets Support Files -> Pods-项目名 -> Pods-项目名-frameworks 中(大约在第44行) 加上 -f 2、CocoaPods版本太旧了,可以尝试升级CocoaPods版本 使用sudo gem update cocoapods更新cocoapods,问题将在1.12.1版本已…...

使用 IPSET 添加 CDN 节点 IP(IPv4/IPv6)到防火墙白名单
明月的服务器一直使用的是 iptables,随着近几年 IPv6 的普及,明月切身体会到还是 IPSET 最方便了,无论你是 IPv4 还是 IPv6 都可以方便的管理,无论你是加入白名单还是黑名单,都非常的简单高效!今天就参照明月自己的实操…...

oracle trim 函数很慢,加trim以后执行超慢,执行计划求解
RT,该字段未建立索引,以下贴出SQL,及执行计划,不加trim走hash join,求解释! ----------------------语句如下,标红的字段加trim() EXPLAIN PLAN FOR select a.楼盘id, a.监测明细id, a.报告日期, a.广告位名称, …...

【Leetcode Python】
偷某间房屋时,累积金额等于间隔前两间房的金额加上当前房的金额数;不偷时,累计金额就等于前一间房的金额数。 状态转移方程:dp[i] max(dp[i-2]nums[i], dp[i-1]) 并且注意错误点:dp[1]有两间房时,初始值为…...

Ubuntu系统的k8s常见的错误和解决的问题
K8s配置的时候出现的常见问题 Q1: master节点kubectl get nodes 出现的错误 或者 解决方法: cat <<EOF >> /root/.bashrc export KUBECONFIG/etc/kubernetes/admin.conf EOFsource /root/.bashrc重新执行 kubectl get nodes 记得需要查看一下自己的…...

Scala学习笔记7: 对象
目录 第七章 对象1- 单例对象2- 伴生对象3- 扩展类或特质的对象4- apply方法5- 应用程序对象6- 枚举end 第七章 对象 在Scala中, 对象(Obiect) 是一个单例实例, 类似于 Java中的单例模式 ; Scala中的对象使用 object 关键字定义, 它可以包含字段、方法、初始化代码和嵌套的类…...
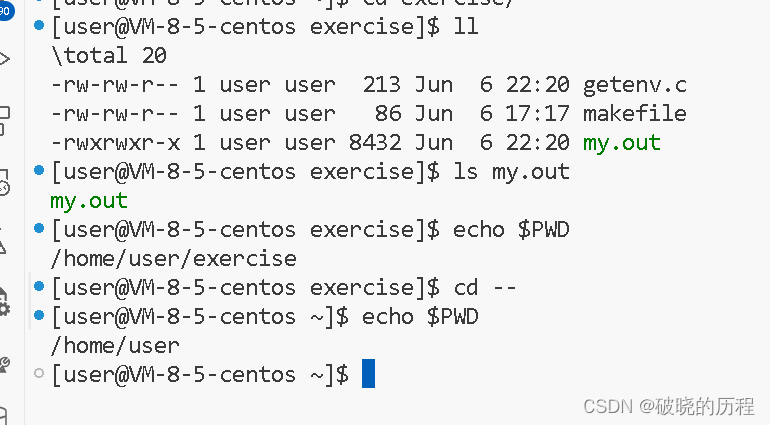
【Linux】进程切换环境变量
目录 一.进程切换 1.进程特性 2.进程切换 1.进程切换的现象 2.如何实现 3.现实例子 2.环境变量 一.基本概念 二.常见环境变量 三.查询常见环境变量的方法 四.和环境变量相关的命令 五.环境变量表的组织方式 六.使用系统调用接口方式查询环境变量 1.getenv 2.反思 …...

嵌入式学习记录6.6(拷贝构造/友元函数/常成员函数)
一.拷贝构造函数和拷贝赋值函数 1.1拷贝构造函数功能,格式 拷贝构造函数是一种特殊的构造函数,用来将一个类对象给另一个类对象初始化使用的。 1> 用一个类对象给另一个类对象初始化时,会自动调用拷贝构造函数。 2> 当一个类对作为函数的实参&…...
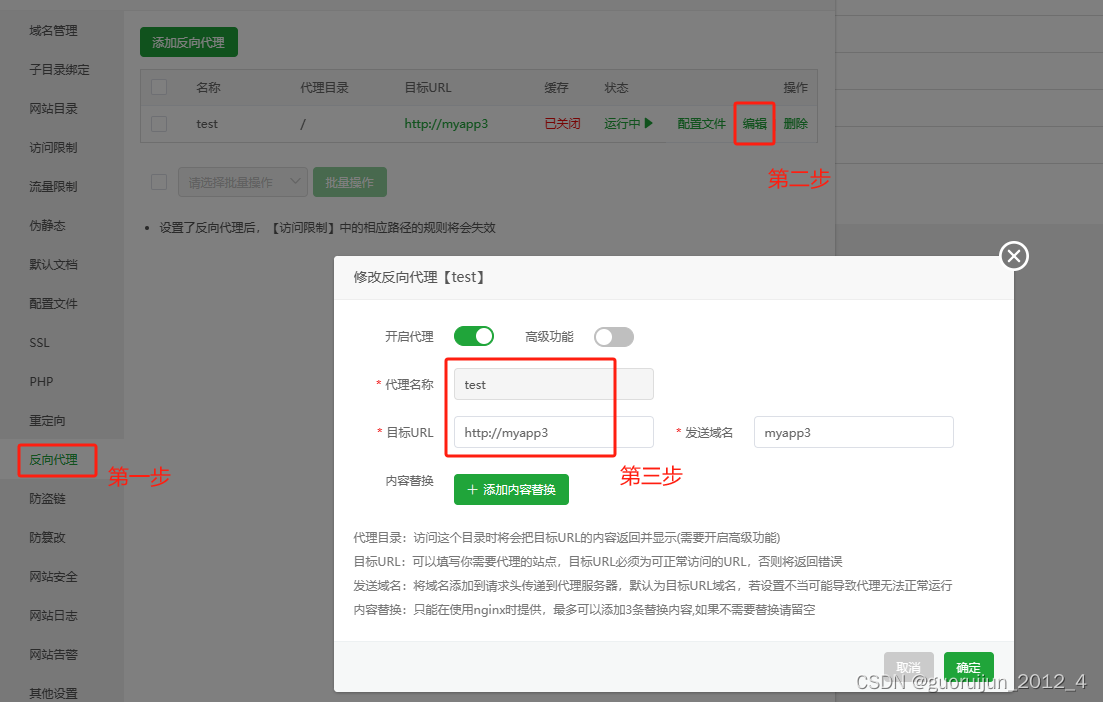
宝塔 nginx 配置负载均衡 upstream
nginx 主配置文件加入 upstream myapp1 {server 192.168.124.101:5051;server 192.168.124.102:5052;server 192.168.124.111:5050;}站点配置文件中加入 location / {proxy_pass http://myapp1;}80端口映射到外网域名配置方法 加入红框中的代码 upstream myapp3 {server 192.16…...

idea 插件推荐
idea 插件推荐 RESTFul-Tool 接口搜索Show Comment 代码注释展示translation 翻译(注释翻译)MyBatisCodeHelperPro 日志封装sql xml跳转GitToolBox 展示GIT提交Jenkins Control idea jenkins 集成Gitmoji Plus: Commit Button GIT提交moji表情 RESTFul-Tool 接口搜索 https://…...
【Linux】Linux环境基础开发工具_5
文章目录 四、Linux环境基础开发工具Linux小程序---进度条git 未完待续 四、Linux环境基础开发工具 Linux小程序—进度条 上篇我们实现了一个简易的进度条,不过那仅仅是测试,接下来我们真正的正式实现一个进度条。 接着编写 processbar.c 文件 然…...
Java Web学习笔记15——DOM对象
DOM: 概念:Document Object Model: 文档对象模型 将标记语言的各个组成部分封装为对应的对象: Document: 整个文档对象 Element:元素对象 Attribute: 属性对象 Text:文本对象 Comment&a…...
中电联系列一:rocket手把手教你理解中电联协议!
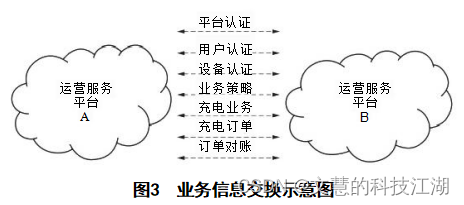
分享《一套免费开源充电桩物联网系统,是可以立马拿去商用的!》 第1部分:总则 Charging and battery swap service information exchange for electric vehicles Part 1:General 前 言 T/CEC102—2016《 电动汽车充换电服务信息交换》分为四…...
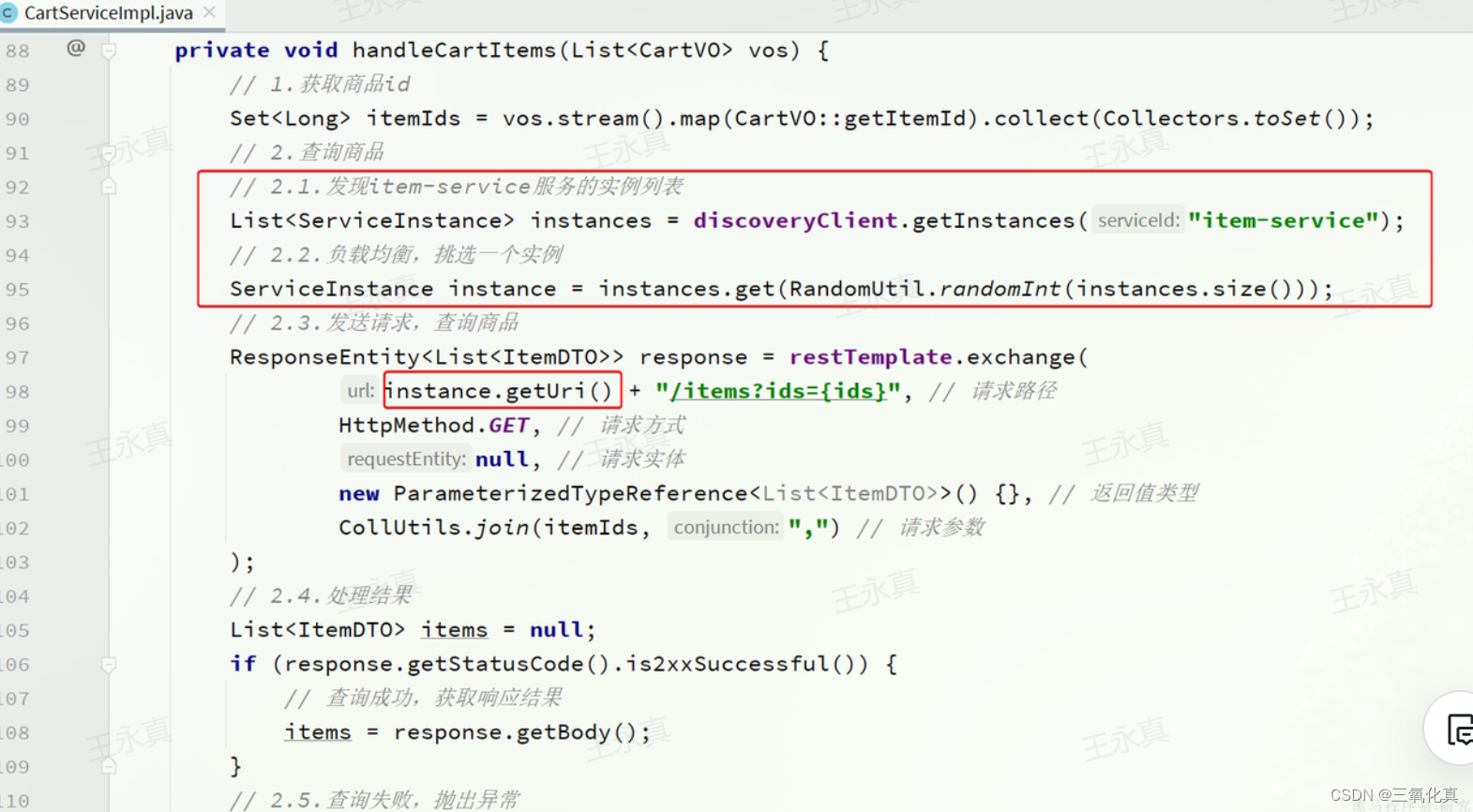
(面试官问我微服务与naocs的使用我回答了如下,面试官让我回去等通知)微服务拆分与nacos的配置使用
微服务架构 正常的小项目就是所有的功能集成在一个模块中,这样代码之间不仅非常耦合,而且修改处理的时候也非常的麻烦,应对高并发时也不好处理,所以 我们可以使用微服务架构,对项目进行模块之间的拆分,每一…...
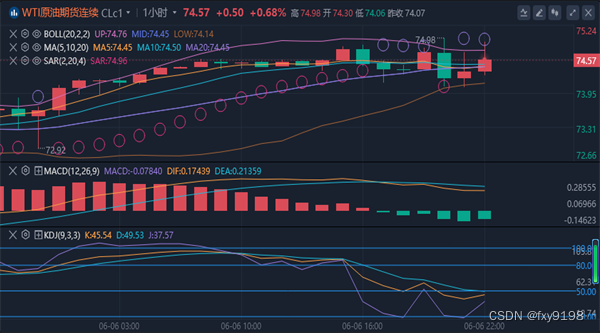
冯喜运:6.7今日黄金原油行情分析及独家操作策略
【黄金消息面分析】:周三(6月5日),金价回升逾1.2%,收盘报每盎司2,355.49美元,全面收复前一交易日的跌幅。周三当天前公布的美国民间就业数据弱于预期,增强了美联储将在今年晚些时候降息的预期&a…...
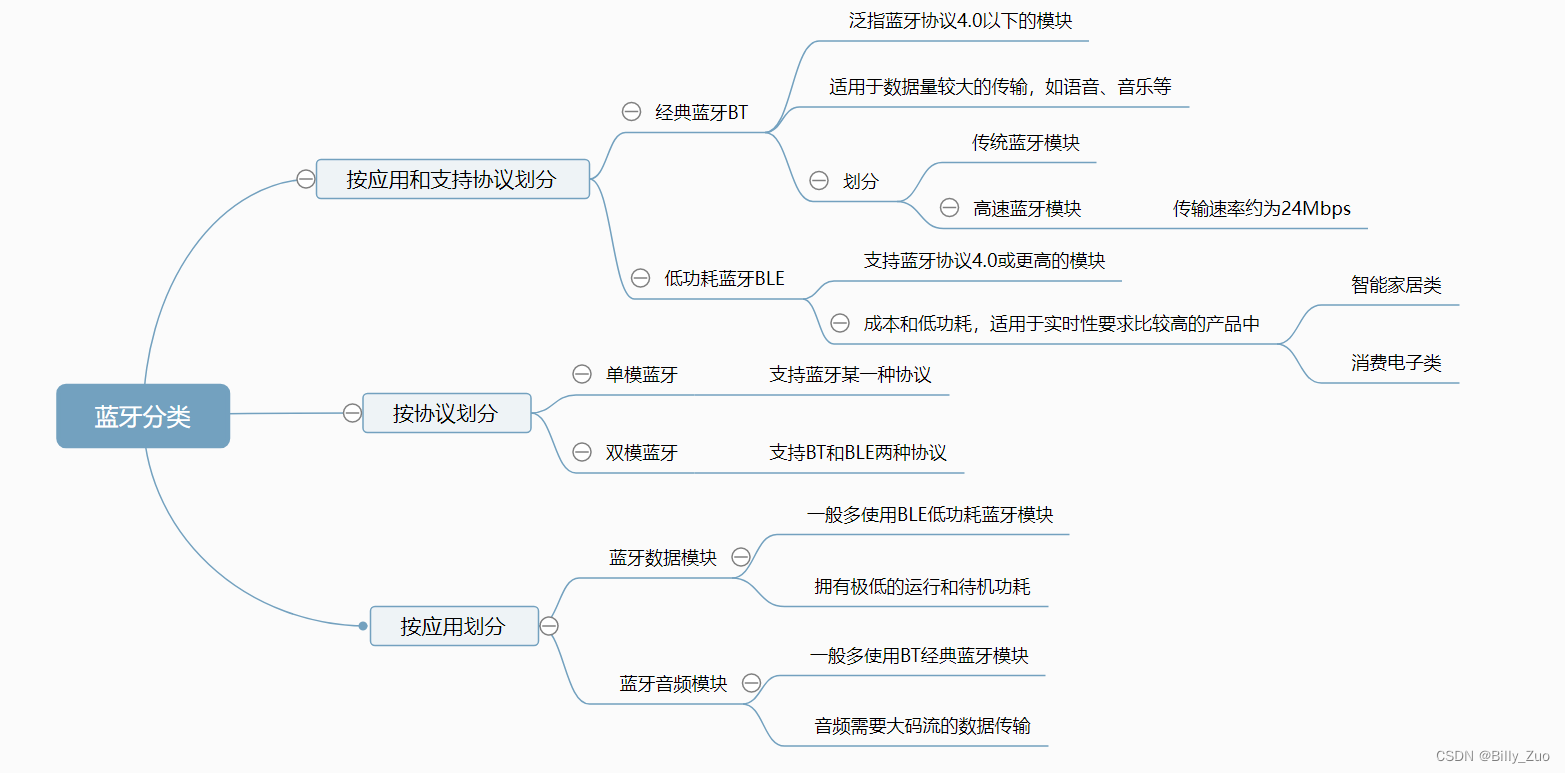
Android 蓝牙概述
一、什么是蓝牙 蓝牙是一种短距离(一般10m内)无线通信技术。蓝牙技术允许固定和移动设备在不需要电缆的情况下进行通信和数据传输。 “蓝牙”这名称来自10世纪的丹麦国王哈拉尔德(Harald Gormsson)的外号。出身海盗家庭的哈拉尔德统一了北欧四分五裂的国…...
、rfind()、index()、rindex())
Python3 笔记:字符串的 find()、rfind()、index()、rindex()
1、find() 方法检测字符串中是否包含子字符串 str ,如果指定 beg(开始) 和 end(结束) 范围,则检查是否包含在指定范围内,如果指定范围内如果包含指定索引值,返回的是索引值在字符串中…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...
