维纳运动的概念
维纳运动(Wiener Process),也称为标准布朗运动,是一种重要的随机过程,广泛应用于数学、物理学和金融学等领域。它是一个连续时间的随机过程,具有一些特殊的性质,使其成为描述随机动态系统的经典模型。维纳运动以奥地利数学家诺伯特·维纳(Norbert Wiener)的名字命名。
维纳运动的定义
维纳运动 W ( t ) W(t) W(t) 是一个具有下列性质的随机过程:
- 初始条件: W ( 0 ) = 0 W(0) = 0 W(0)=0。
- 独立增量:对于任意的 0 ≤ t 1 < t 2 < ⋯ < t n 0 \leq t_1 < t_2 < \cdots < t_n 0≤t1<t2<⋯<tn,增量 W ( t k ) − W ( t k − 1 ) W(t_k) - W(t_{k-1}) W(tk)−W(tk−1)是相互独立的。
- 正态增量:对于任意 s < t s < t s<t,增量 W ( t ) − W ( s ) W(t) - W(s) W(t)−W(s)服从均值为 0、方差为 t − s t - s t−s 的正态分布,即 W ( t ) − W ( s ) ∼ N ( 0 , t − s ) W(t) - W(s) \sim N(0, t - s) W(t)−W(s)∼N(0,t−s)。
- 连续路径:函数 t ↦ W ( t ) t \mapsto W(t) t↦W(t)几乎处处是连续的。
数学表示
维纳运动的数学表示为:
W ( t ) ∼ N ( 0 , t ) W(t) \sim N(0, t) W(t)∼N(0,t)
这意味着对于任意时间 t t t,维纳运动 W ( t ) W(t) W(t) 服从均值为 0、方差为 t t t的正态分布。
性质
- 独立增量:维纳运动在不同时间段的增量相互独立。
- 正态分布:增量 ( W(t) - W(s) ) 服从正态分布,均值为 0,方差为 ( t - s )。
- 平稳增量:增量的分布只与时间间隔的长度有关,而与具体时间无关。
- 连续性:维纳运动的路径几乎处处连续,但几乎处处不可微。
应用
维纳运动在多个领域有广泛应用:
- 金融数学:维纳运动是Black-Scholes期权定价模型的基础,用于建模股票价格和其他金融资产。
- 物理:用于描述微粒在流体中的随机运动,经典的布朗运动即是维纳运动的物理模型。
- 生物:用于建模生物体内的分子运动。
- 工程:用于建模随机信号和噪声。
示例
假设我们有一个维纳运动 W ( t ) W(t) W(t)。在时间 t = 0 t = 0 t=0 时, W ( 0 ) = 0 W(0) = 0 W(0)=0。对于任意时间 t t t,我们可以计算维纳运动的值 W ( t ) W(t) W(t),例如:
- W ( 1 ) ∼ N ( 0 , 1 ) W(1) \sim N(0, 1) W(1)∼N(0,1)
- W ( 2 ) ∼ N ( 0 , 2 ) W(2) \sim N(0, 2) W(2)∼N(0,2)
- 增量 W ( 2 ) − W ( 1 ) ∼ N ( 0 , 1 ) W(2) - W(1) \sim N(0, 1) W(2)−W(1)∼N(0,1),且与 W ( 1 ) W(1) W(1) 独立。
这些性质使得维纳运动在描述随机动态系统时具有很大的灵活性和实用性。
结论
维纳运动是一个基本的随机过程模型,因其独特的性质和广泛的应用而备受关注。它不仅是理论研究的重要工具,也是解决实际问题的有力工具。掌握维纳运动的基本概念和性质,对于深入理解随机过程以及相关领域的应用具有重要意义。
相关文章:

维纳运动的概念
维纳运动(Wiener Process),也称为标准布朗运动,是一种重要的随机过程,广泛应用于数学、物理学和金融学等领域。它是一个连续时间的随机过程,具有一些特殊的性质,使其成为描述随机动态系统的经典…...
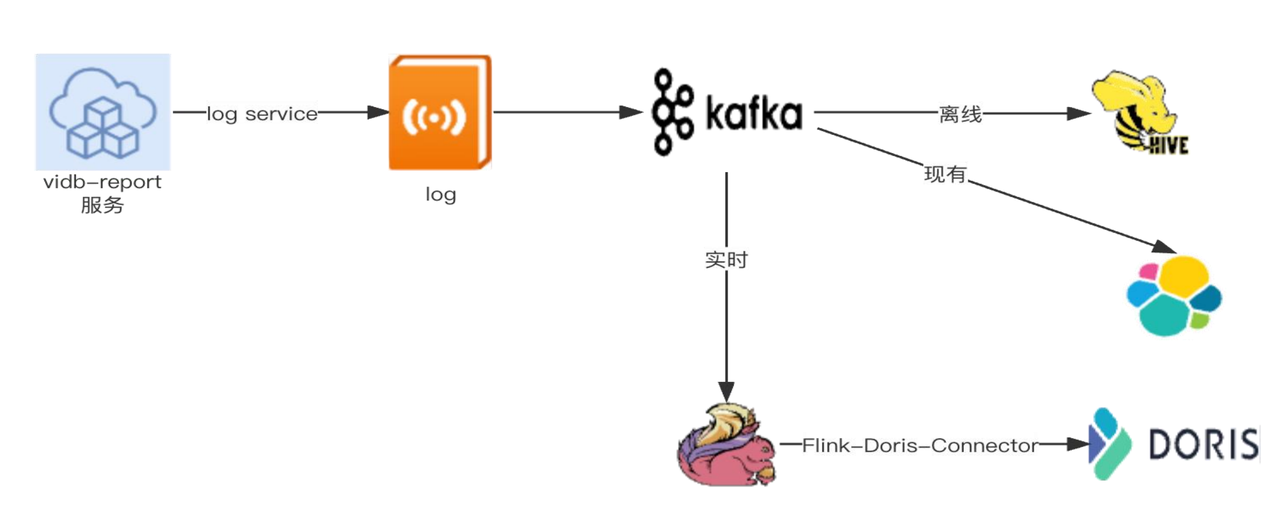
毫秒级查询性能优化实践!Apache Doris 在极越汽车数字化运营和营销方向的解决方案
作者:韩同阳,极越汽车大数据架构师,Apache Doris Active Contributor 编辑整理:SelectDB 技术团队 导读:极越是高端智能汽车机器人品牌,基于领先的百度 AI 能力和吉利 SEA 浩瀚架构生态赋能,致…...

vllm 大模型量化微调推理使用: lora、gptq、awq
1)微调lora模型推理 docker run --gpus all -v /ai/Qwen1.5-7B-Chat:/qwen-7b -v /ai/lora:/lora -p 10860:10860 --...
 自动测评方法)
WPS/Office(Word、Excel、PPT) 自动测评方法
在各高等、中等院校的计算机类课程中,计算机基本应用技能的上机操作考试,广受重视,大为盛行。其中,office(word、excel、ppt)上机考试最为普遍。于是,实现这类Office文档操作的自动阅卷评分,很有必要。本人最近项目上刚好遇到需要解决这种自动评分的问题,所以再次记录下解决的…...

ArrayList——简单洗牌算法
特殊语法介绍: List<List<E>> 该语法情况比较特殊,相当于一个“二维数组”存着一个个线性表的结构,如图: 该语法的灵活性强,可适用于多种类型和多种情况。接下来就使用该语法来实现一个简单的洗牌操作。…...
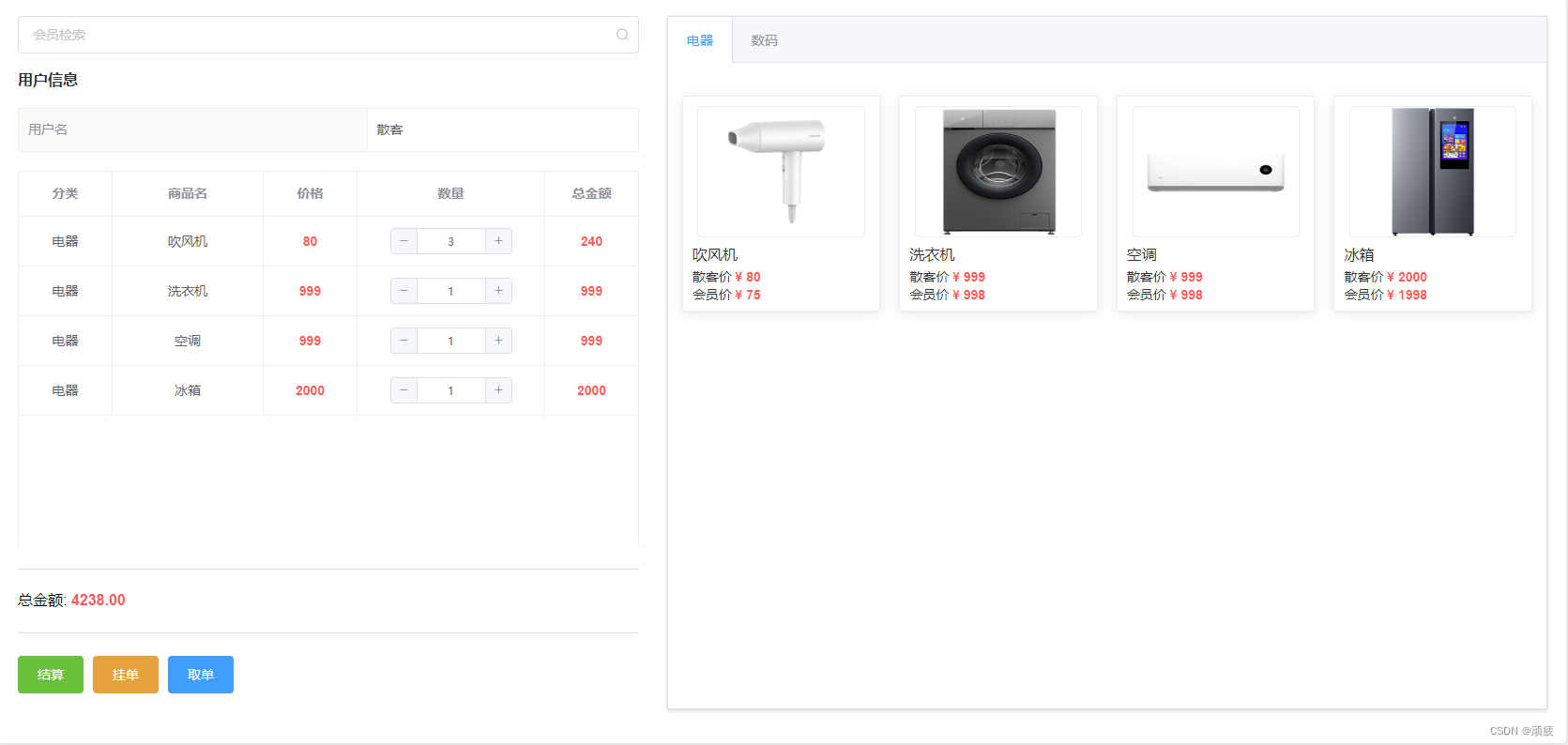
springboot vue 开源 会员收银系统 (6) 收银台的搭建
前言 完整版演示 前面我们对会员系统 分类和商品的开发 完成了收银所需的基础信息 下面我们开始完成收银台的开发 简单画了一个收银的流程图大家参考下 从这张图我们可以分析一下几点 可以选择会员或散客收银选择会员使用相应的会员价结算使用会员卡则在价格基础根据卡折扣…...

重排和重绘的区别,什么情况下会触发这两种情况
重排(Reflow)和重绘(Repaint)是Web前端开发中关于浏览器渲染机制的两个核心概念。它们之间的主要区别以及触发条件如下: 重排(Reflow) 定义: 重排也称为布局(Layout&a…...

亮点回顾|智能汽车芯片创新技术应用与质量研讨会
5月29日,2024汽车软件与通信大会——智能汽车芯片创新技术应用与质量研讨会在江苏苏州狮山国际会议中心举行。本次会议由中国中检所属中国汽车工程研究院股份有限公司(简称:中国汽研)主办,旨在为智能汽车芯片的技术创新…...

特征工程,减小过拟合
目录 特征工程 减小过拟合 图像增强方法 特征工程是机器学习和数据分析中不可或缺的一环,其重要性不言而喻。以下是关于特征工程的详细回答: 一、定义 特征工程是将原始数据转化为更好的表达问题本质的特征的过程,旨在发现对因变量y有明显影响作用的特征(通常称自变量…...

STM32-16-ADC
STM32-01-认识单片机 STM32-02-基础知识 STM32-03-HAL库 STM32-04-时钟树 STM32-05-SYSTEM文件夹 STM32-06-GPIO STM32-07-外部中断 STM32-08-串口 STM32-09-IWDG和WWDG STM32-10-定时器 STM32-11-电容触摸按键 STM32-12-OLED模块 STM32-13-MPU STM32-14-FSMC_LCD STM32-15-DMA…...
)
单例模式(C语言)
C语言的设计模式(单例模式) 单例模式(Singleton Pattern)是一种设计模式,目的是确保一个类只有一个实例,并提供一个全局访问点。 #include "stdio.h" #include "stdlib.h"// 定义一个…...

js前端格式化日期函数
开发需求 在前端中我们通常使用new Date()函数获取到的日期时间是下面这种样子:Thu Jun 06 2024 17:29:11 GMT0800 (中国标准时间),我们想要把它转换成常见的指定格式,比如 年-月-日 时:分:秒年/月/日 时:分:秒年-月-日年/月/日 所以就封装…...
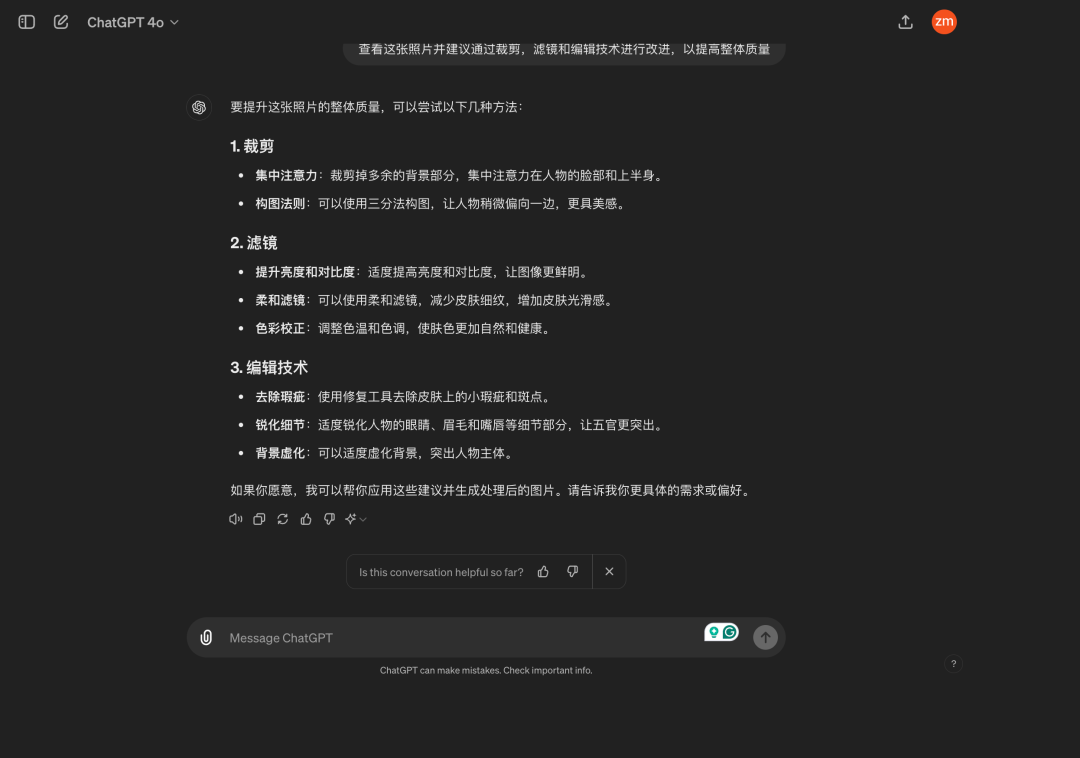
五个超实用的 ChatGPT-4o 提示词
GPT-4o 是 OpenAI 最近推出的最新人工智能模型,不仅具备大语言模型的能力,而且拥有多模态模型的看、读、说等能力,而且速度比 GPT-4 更快。下面我们就来介绍几个超实用的 GPT-4o 提示词,帮助大家更好地了解 GPT-4o 的功能和应用场…...

基于51单片机多功能防盗报警proteus仿真( proteus仿真+程序+设计报告+原理图+讲解视频)
基于51单片机多功能防盗报警系统 1. 主要功能:2. 讲解视频:3. 仿真4. 程序代码5. 设计报告6. 原理图7. 设计资料内容清单&&下载链接 基于51单片机多功能防盗报警系统( proteus仿真程序设计报告原理图讲解视频) 仿真图proteus8.9及以上…...
gitee和github的协同
假设gitee上zhaodezan有一个开发库,但是从andeyeluguo上拉取最新的(从github上同步过来最新的) git remote add dbgpt_in_gitee https://gitee.com/andeyeluguo/DB-GPT.git remote -v git pull --rebase dbgpt_in_gitee main 有冲突可能需要…...
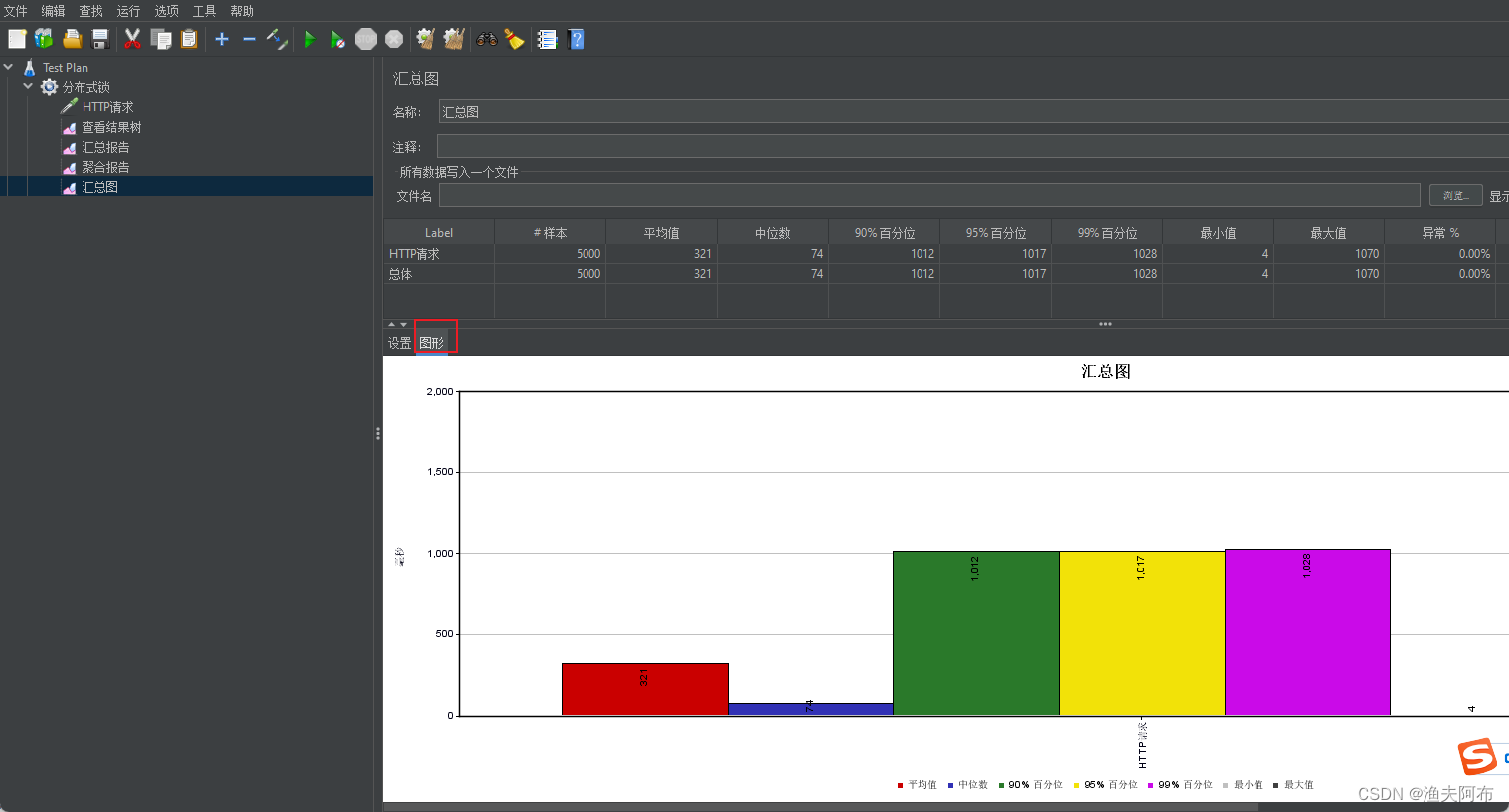
压力测试-性能指标-Jmeter使用-压力测试报告
文章目录 1.压测目的2.性能指标3.Jmeter3.1Jmeter使用3.1.1 运行Jmeter3.1.2 添加线程组3.1.3设置HTTP请求3.1.4 设置监视器 3.2 查看Jmeter压测结果3.2.1 查看结果树3.2.2 查看汇总报告3.2.3 查看聚合报告3.2.4 查看汇总图 1.压测目的 内存泄漏:OOM,重…...

通过Slf4j中的MDC实现在日志中添加用户IP功能
一、slf4j中MDC是什么 slf4j除了trace、debug、info、warn、error这几个日志接口外,还可以配合MDC将数据写入日志。换句话说MDC也是用来记录日志的,但它的使用方式与使用日志接口不同。 在使用日志接口时我们一般这么做 log.debug("log debug"…...

代码随想录算法训练营第四十九天| 139.单词拆分、背包问题总结
139.单词拆分 题目链接:139.单词拆分 文档讲解:代码随想录/单词拆分 视频讲解:视频讲解-单词拆分 状态:已完成(0遍) 解题过程 这几天博主忙着面试和入职,一晃已经周四了,这个礼拜…...

STM32F103VE和STM32F407VE的引脚布局
STM32F103VE vs STM32F407VE 引脚对比表 引脚 STM32F103VE STM32F407VE 备注 1 VSS VSS 地 2 VDD VDD 电源 3 VSSA VSSA 模拟地 4 VDDA VDDA 模拟电源 5 OSC_IN OSC_IN 外部时钟输入 6 OSC_OUT OSC_OUT 外部时钟输出 7 NRST NRST 复位 8 PC13 (GPIO) PC13 (GPIO) GPIO 9 PC14 (…...

搜维尔科技:使用 Xsens 动作捕捉技术创建栩栩如生的动画
使用Xsens 动作捕捉技术创建栩栩如生的动画 搜维尔科技:使用 Xsens 动作捕捉技术创建栩栩如生的动画...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
