inflight 守恒和带宽资源守恒的有效性
接着昨天的问题,inflight 守恒的模型一定存在稳定点吗?并不是。如果相互抑制强度大于自我抑制强度,系统也会跑飞:
模拟结果如下:
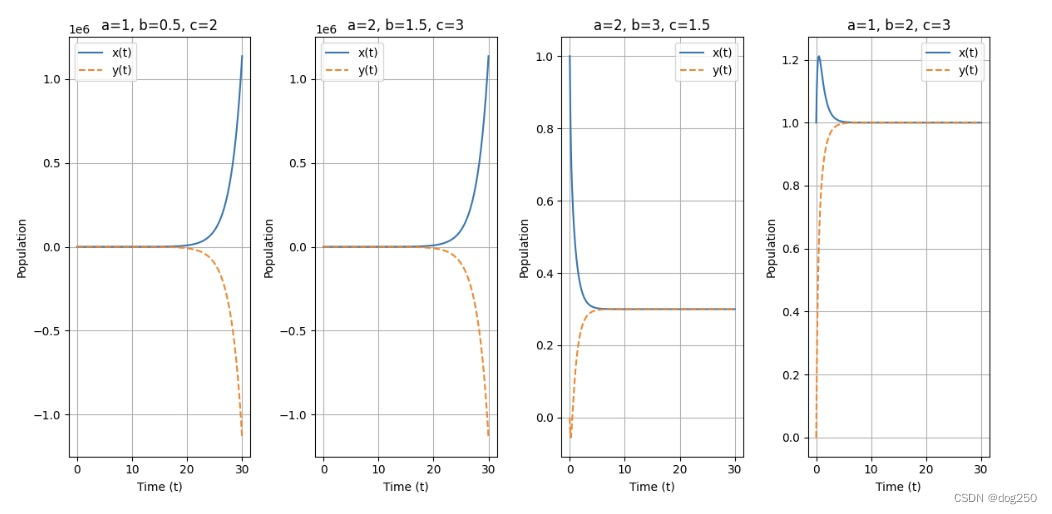
所以一定要记得 a < b。
比对前两个图和后两个图的 a,b 参数关系,即可得道。接下来的问题是,即使 a < b,这一切图景,是一厢情愿吗?对于一种端到端 capacity-seeking 算法的衍生,震荡是本质属性,E_best = max(bw / delay) 共识又何德何能?
抛开 E_best 共识本身,先论证稳定收敛点的存在性,这是一个典型的资源消耗模型,但更简单些。系统表达如下,设 x 为流量,y 为带宽和 buffer 等承载流量的资源,则有:
d x d t = a ∗ y − b ∗ x \dfrac{dx}{dt}=a*y-b*x dtdx=a∗y−b∗x
d y d t = − c ∗ x ∗ y + d ∗ x \dfrac{dy}{dt}=-c*x*y+d*x dtdy=−c∗x∗y+d∗x
x 的变化受两方面影响,它的生成速度与资源成正比,同时其消亡速度与其本身成正比,而资源 y 也受两方面影响,首先,更多的 x 会消耗更多资源,更充足的 y 会使其消耗更快(本性?),其次,如果有 x 退出,y 会增长。模拟结果如下:
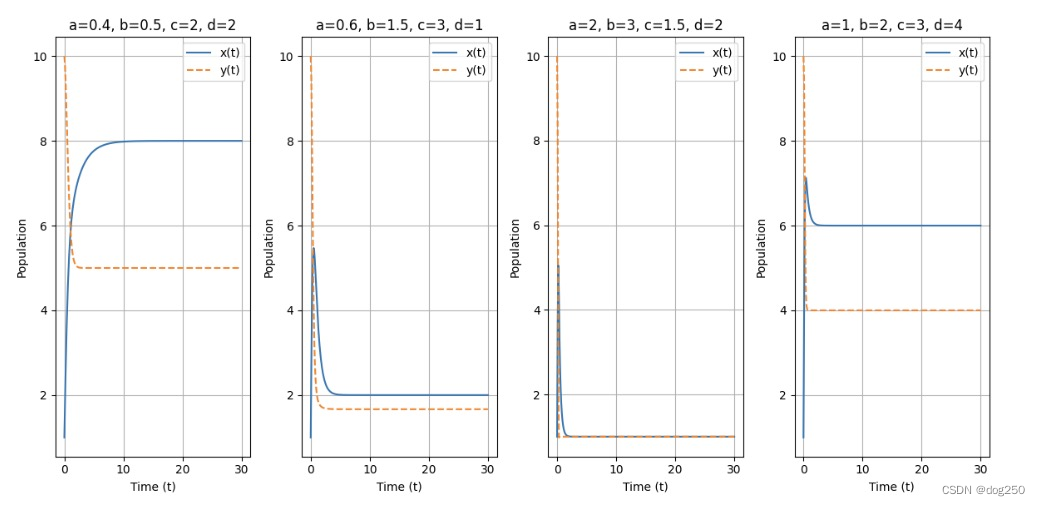
都可以稳定收敛。注意图 1 的参数,它甚至没有震荡。
就着这个模拟,说点有趣的,把系统稍微变一下,如果资源可再生,而不是守恒,系统表达式的 y 将是:
d y d t = − c ∗ x ∗ y + d ∗ y \dfrac{dy}{dt}=-c*x*y+d*y dtdy=−c∗x∗y+d∗y
看下会怎样:
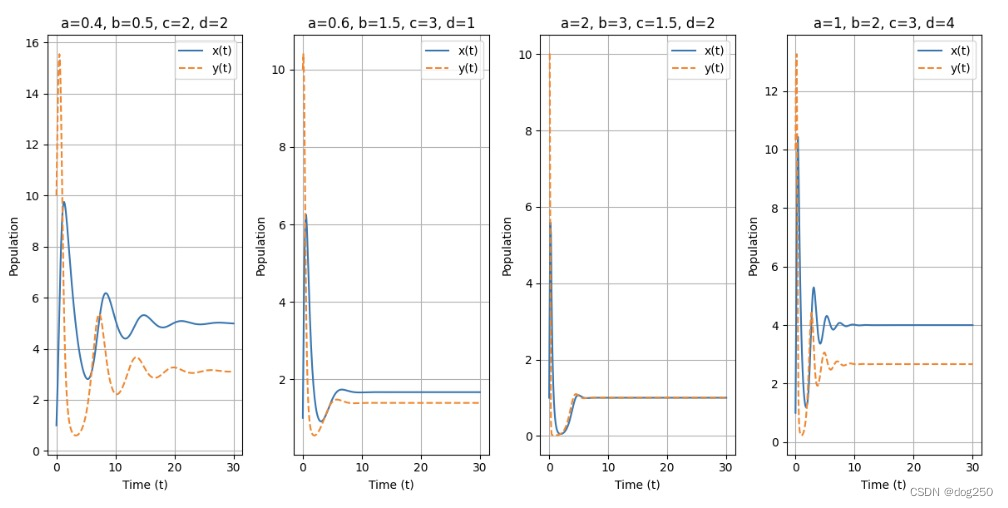
系统竟然震荡了,且资源利用率并不高。所以,基于守恒,自己玩自己,只要调得一手好参数,不愁不高效。只要 E_best 共识被识别,流量守恒,资源守恒,不断腾挪(想象一下,早高峰的公交车刚开始非常拥挤,晃荡一阵子后就不拥挤了,但也上不来人了),最终就是效率和公平双百分。
再说个敏感的,如果资源不可再生,已消费资源不可腾挪重归资源池,且消费者有趋之若鹜的倾向呢?比如看到人越多就越去凑热闹,x 将改为:
d x d t = a ∗ c ∗ x ∗ y − b ∗ x \dfrac{dx}{dt}=a*c*x*y-b*x dtdx=a∗c∗x∗y−b∗x
结果如下:

像不像安得广厦千万间,大庇天下寒士俱欢颜的奢望,到底是鸡飞蛋打一场空,越是疯狂越是奔赴,最终延迟的报应越猛烈,双归零。
浙江温州皮鞋湿,下雨进水不会胖。
相关文章:

inflight 守恒和带宽资源守恒的有效性
接着昨天的问题,inflight 守恒的模型一定存在稳定点吗?并不是。如果相互抑制强度大于自我抑制强度,系统也会跑飞: 模拟结果如下: 所以一定要记得 a < b。 比对前两个图和后两个图的 a,b 参数关系&am…...
短视频直播教学课程小程序的作用是什么
只要短视频/直播做的好,营收通常都不在话下,近些年,线上自媒体行业热度非常高,每条细分赛道都有着博主/账号,其各种优势条件下也吸引着其他普通人冲入。 然无论老玩家还是新玩家,面对平台不断变化的规则和…...

Open AI又出王炸GPT-4,目测一大波人的饭碗要碎了...
前言 在科技的惊涛骇浪中,每一次技术的飞跃都预示着新时代的曙光。近日,Open AI公司再次震撼业界,推出了其最新力作——GPT-4,这款被誉为“王炸”的语言模型,以其前所未有的智能水平和创造力,不仅在技术圈…...
:转移指令的原理)
8086 汇编笔记(八):转移指令的原理
一、操作符 offset 操作符offset在汇编语言中是由编译器处理的符号,它的功能是取得标号的偏移地址 codesg segmentstart: mov ax,offset start ;相当于 mv ax,0s: mov ax,offset s ;相当于 mv ax,3codesg endsend start 二、jmp 指令 jmp为无条件…...

win 系统 cmd 命令从私库上传,下载jar包
1. 确保maven环境变量或者maven安装无误; 2.私库下载 命令 mvn dependency:get -DgroupId<your_group_id> -DartifactId<your_artifact_id> -Dversion<your_version> -Dpackagingjar -Dfile<path_to_your_jar_file> -Durl<your_privat…...

dots_image 增强图像中的圆点特征
dots_image 增强图像中的圆点特征 1. dot_image 有什么用途?2. 点状字符的特征增强3. Halcon代码 1. dot_image 有什么用途? Enhance circular dots in an image. 这个算子可以增强图像中的圆点特征,例如下面的例子。 2. 点状字符的特征增强…...

代码随想录算法训练营第十五天| 110.平衡二叉树、 257. 二叉树的所有路径、404.左叶子之和
110.平衡二叉树 题目链接:110.平衡二叉树 文档讲讲:代码随想录 状态:还可以 思路:计算左右子树的深度差,递归判断左右子树是否符合平衡条件 题解: public boolean isBalanced(TreeNode root) {if (root n…...

MSP430单片机控制流水灯,Proteus仿真
作品功能 本项目利用MSP430单片机控制一个简单的流水灯,通过按键切换流水灯的模式。用户可以通过按键控制LED灯的方向,从左向右或从右向左依次点亮。 作品的硬件材料 MSP430单片机 具体型号:MSP430G2553 LED灯 数量:8个类型&…...

出售iPhone前的必做步骤:完全擦除个人数据的方法
当您准备在闲鱼上转售旧 iPhone、将其捐赠、送给朋友或通过 Apple 回收之前,您可能会选择执行“恢复”操作来擦除您的数据。但请注意,这一操作并不能真正删除设备中的数据。被“删除”或“格式化”的数据实际上仍存在于 iPhone 中,只是被系统…...

npm yarn 更换国内源以及node历史版本下载地址
npm 更换国内源 npm config set registryhttps://registry.npmmirror.com npm config set electron_mirrorhttps://registry.npmmirror.com/electron/yarn 更换国内源 yarn config set registry https://registry.npmmirror.comnode历史版本下载地址 https://nodejs.org/dow…...

微信小程序手机号码授权登录
文章目录 一、微信小程序开发二、使用步骤1.前端代码2.后台配置3.后台代码 总结 一、微信小程序开发 目前个人的小程序无法使用手机号码授权登录,可以使用测试号进行开发 二、使用步骤 1.前端代码 代码如下(示例): <butto…...

【网络编程开发】1.网络结构 2.IP地址与端口号 3.字节序
网络编程开发 两台计算机要互相传送文件需解决很多问题: 必须有一条传送数据的通路。发起方必须激活通路。要告诉网络如何识别接收方。发起方要清楚对方是否已开机,且与网络连接正常。发起方要清楚对方是否准备好接收和存储文件。若文件格式不兼容&…...

读取文件
自学python如何成为大佬(目录):自学python如何成为大佬(目录)_利用python语言智能手机的默认语言实战一-CSDN博客 在Python中打开文件后,除了可以向其写入或追加内容,还可以读取文件中的内容。读取文件内容主要分为以下几种情况: 1 读取指…...
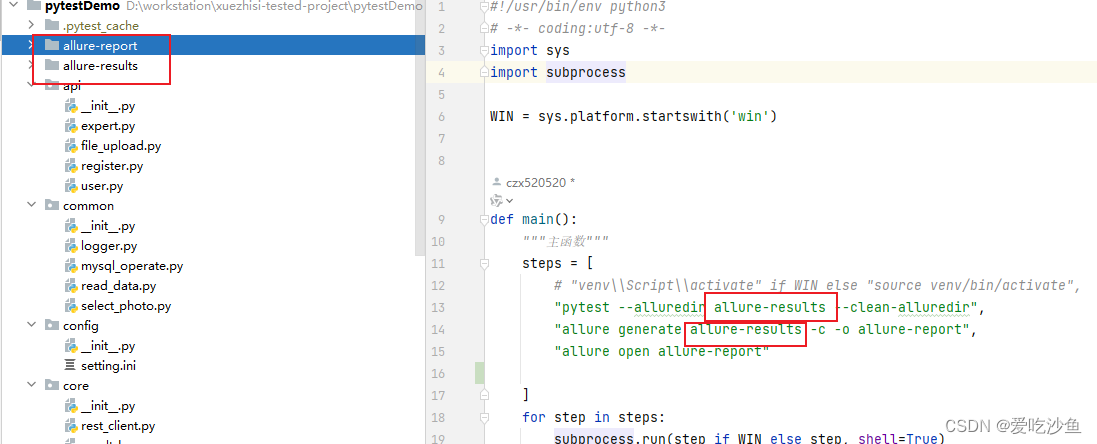
Allure在jenkins中无法显示的问题
jenkins中使用allure生成报告需要注意工作环境和路径的配置 前提条件: jenkins容器中已安装jdk和allure jenkins中配置全局工具环境: 项目中配置allure路径: 路径来源: Path需要选择相对路径的allure-report、allure-results...
建筑建筑一建考试试题及答案,分享几个实用搜题和学习工具 #其他#职场发展
收录了大量考试类型的题库,大到考公,小到知识竞赛,题库资源算是比较丰富的了。操作起来也不难,我们只需输入题目内容,即可快速搜索出答案,而且它在给出答案的同时还会附带解析。最重要的是,搜题…...

[240607] Jina AI 发布多模态嵌入模型 | PHP 曝新漏洞 | TypeScript 5.5 RC 发布公告
目录 Jina AI 多模态嵌入模型 - jina-clip-v1PHP 漏洞 CVE-2024-4577TypeScript 5.5 RC 发布公告 Jina AI 多模态嵌入模型 - jina-clip-v1 jina-clip-v1 是 Jina AI 最新推出的多模态嵌入模型。与 OpenAI CLIP 相比,它大幅提升了纯文本检索方面的性能,同…...
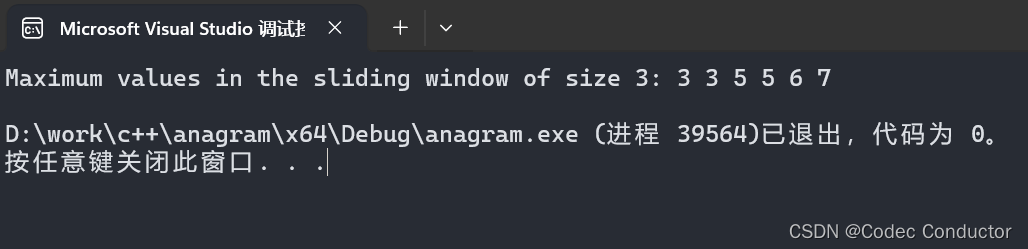
LeetCode 算法:滑动窗口最大值c++
原题链接🔗:滑动窗口最大值 难度:困难⭐️⭐️⭐️ 题目 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动…...

荆州餐饮环保在行动:清洗油烟净化器,守护城市环境
我最近分析了餐饮市场的油烟净化器等产品报告,解决了餐饮业厨房油腻的难题,更加方便了在餐饮业和商业场所有需求的小伙伴们。 在荆州,餐饮业不仅是美食爱好者的天堂,更是城市生活的重要组成部分。然而,随着餐饮业的发…...

AIConnect赋能加持丨AI+DEPIN 共同推动AI发展的技术与运用峰会圆满落幕
6月6日,由AIConnect主办,JuCoin协办的「AIDePIN 共同推动AI发展的技术与应用」峰会在胡志明市圆满落幕!此次活动不仅是AIConnect生态在市场推广和技术应用方面的重要一步,也标志着JuCoin在推动AI与DePIN技术融合中的又一里程碑。 …...

【自定义View】Android圆饼进度条
源码 自定义属性 <?xml version"1.0" encoding"utf-8"?> <resources><declare-styleable name"ArcProgressView"><attr name"android:textSize" /><attr name"bgBorderWidth" format"d…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
