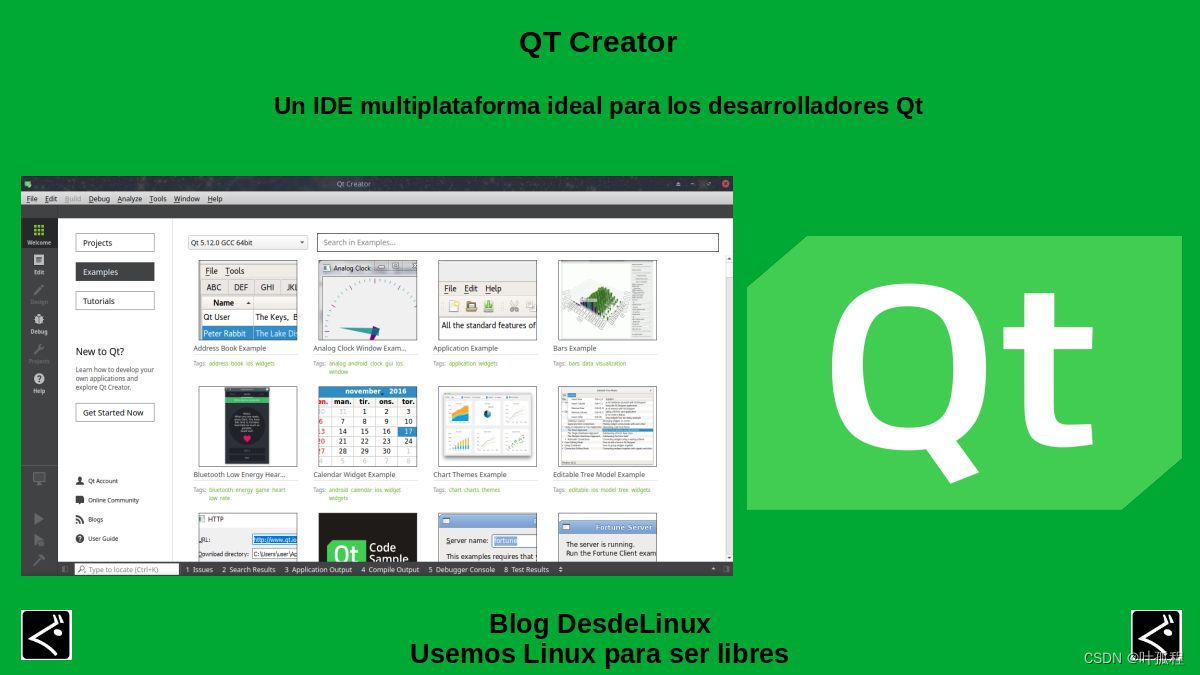
【Qt知识】部分QWidget属性表格
QWidget是Qt库中所有图形用户界面组件的基类,它提供了大量属性以供自定义和配置控件的行为和外观。下面列出了一些主要的QWidget属性及其作用。
| 属性 | 作用 |
| accessibleName | 控件的辅助技术名称,用于无障碍访问。 |
| accessibleDescription | 控件的辅助技术描述,用于无障碍访问。 |
| autoFillBackground | 如果为真,则使用调色板中的背景颜色自动填充控件。 |
| backgroundRole | 调色板角色,用于确定背景颜色。 |
| cursor | 显示在控件上的光标类型。 |
| dragEnabled | 是否允许从控件开始拖放操作。 |
| dropEnabled | 是否允许向控件执行拖放操作。 |
| font | 控件的字体设置。 |
| focusPolicy | 控件获取焦点的策略。 |
| foregroundRole | 调色板角色,用于确定前景颜色。 |
| geometry | 控件的位置和大小。 |
| hidden | 控件是否隐藏。 |
| iconSize | 如果控件显示图标,此属性定义图标的大小。 |
| inputMethodHints | 控件的输入法提示。 |
| layoutDirection | 控件的布局方向,如左至右或右至左。 |
| locale | 控件的区域设置。 |
| minimumSize | 控件的最小尺寸。 |
| maximumSize | 控件的最大尺寸。 |
| palette | 控件的调色板,影响控件的颜色方案。 |
| sizePolicy | 控件的尺寸策略,决定控件如何响应布局变化。 |
| sizeIncrement | 控件尺寸增量,用于某些布局中的对齐。 |
| styleSheet | CSS样式的字符串,用于设置控件的样式。 |
| tabOrder | 在Tab键导航中的顺序。 |
| toolTip | 当鼠标悬停在控件上时显示的工具提示。 |
| windowFlags | 控件的窗口标志,影响窗口的行为和外观。 |
| windowModality | 控件的模态级别,确定控件如何与其他窗口交互。 |
| windowTitle | 控件的标题,如果控件是一个顶级窗口。 |
| windowOpacity | 控件的透明度。 |
| frameShape | 控件的边框形状,如果控件是一个QFrame。 |
| frameShadow | 控件的边框阴影,如果控件是一个QFrame。 |
| textInteractionFlags | 文本控件的交互标志,如是否允许选择文本。 |
| windowIcon | 控件的图标,如果控件是一个顶级窗口。 |
| antialiasing | 字体抗锯齿设置,影响文本的清晰度。 |
| kerning | 字符间距调整,影响文本字符间的间距。 |

以上属性可以通过QWidget的成员函数进行访问和修改,例如setFont(), setGeometry(), setStyleSheet()等。此外,QWidget还提供了信号和槽机制,允许在属性改变时触发事件处理。
请注意,不是所有属性都适用于所有类型的QWidget子类,具体可用性取决于具体的控件类型。例如,textInteractionFlags属性只对那些能够显示文本的控件有意义。
相关文章:

【Qt知识】部分QWidget属性表格
QWidget是Qt库中所有图形用户界面组件的基类,它提供了大量属性以供自定义和配置控件的行为和外观。下面列出了一些主要的QWidget属性及其作用。 属性 作用 accessibleName 控件的辅助技术名称,用于无障碍访问。 accessibleDescription 控件的辅助技…...

【ARM64 常见汇编指令学习 19.1 -- ARM64 跳转指令 b.pl 详细介绍】
文章目录 ARM64 跳转指令 b.pl使用场景语法示例总结 ARM64 跳转指令 b.pl 在 ARMv8 架构中,b.pl 是一条条件分支(Branch)指令,它根据当前的状态寄存器中的条件标志执行跳转。b.pl 的全称是 Branch if Plus,即如果条件…...

WWDC24即将到来,ios18放大招
苹果公司即将在下周开全球开发者大会(WWDC),大会上将展示其人工智能技术整合到设备和软件中的重大进展,包括与OpenAI的历史性合作。随着大会的临近,有关iOS 18及其据称采用AI技术支持的应用程序和功能的各种泄露信息已经浮出水面。 据报道,苹果将利用其自主研发的大…...

C#中的空合并运算符与空合并赋值运算符:简化空值处理
在C#编程中,处理可能为null的值是一项常见的任务,尤其是在涉及数据库查询、Web服务调用或任何可能返回缺失数据的场景中。为了简化这类操作并提高代码的可读性,C# 8 引入了两个非常实用的运算符:空合并运算符 (??) 和 空合并赋值…...

数据结构:哈夫曼树及其哈夫曼编码
目录 1.哈夫曼树是什么? 2.哈夫曼编码是什么? 3.哈夫曼编码的应用 4.包含头文件 5.结点设计 6.接口函数定义 7.接口函数实现 8.哈夫曼编码测试案列 哈夫曼树是什么? 哈夫曼树(Huffman Tree)是一种特殊的二叉树…...
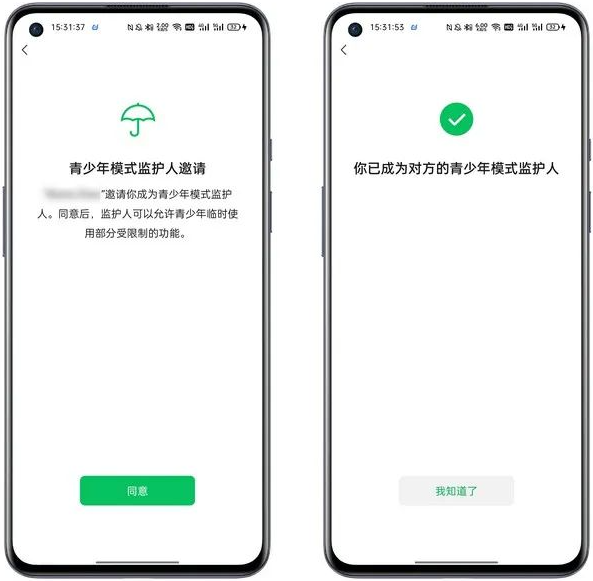
微信如何防止被对方拉黑删除?一招教你解决!文末附软件!
你一定不知道,微信可以防止被对方拉黑删除,秒变无敌。只需一招就能解决!赶快来学!文末有惊喜! 惹到某些重要人物(比如女朋友),被删除拉黑一条龙,那真的是太令人沮丧了&a…...

jar增量打包
jar增量打包 Linux环境下: 1.解压缩 jar -xvf jarname.jar(解压)2.打包 这时可以把要替换的lib包的内容粘帖进去,然后重新打jar包 jar -cvf0M jarname.jar .(重新压缩,-0是主要的)jar命令: …...

智慧医院物联网建设-统一管理物联网终端及应用
近年来,国家卫健委相继出台的政策和评估标准体系中,都涵盖了强化物联网建设的内容。物联网建设已成为智慧医院建设的核心议题之一。 作为医院高质量发展的关键驱动力,物联网的顶层设计与网络架构设计规划,既需要结合现代信息技术的…...

Debian的常用命令
Debian作为一个稳定、安全且高效的Linux发行版,被广泛应用于服务器和桌面操作系统中。对于系统管理员和开发者来说,熟练掌握Debian的常用命令能够大大提升工作的效率和系统的管理水平。本文将详细介绍一些常见且实用的Debian命令,帮助新手更好地管理和操作Debian系统。 系统…...

矩阵1-范数与二重求和的求和可交换
矩阵1-范数与二重求和的求和可交换 1、矩阵1-范数 A [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] A \begin{bmatrix} a_{11} &a_{12} &\cdots &a_{1n} \\ a_{21} &a_{22} &\cdots &a_{2n} \\ \vdots &\vdots …...

Python笔记 - *args和**kwargs
探索Python的*args和**kwargs 在Python中,函数可以接受任意数量的参数,而这要归功于*args和**kwargs的强大功能。这两个特性使得函数在处理不同数量的输入时变得更加灵活和高效。在这篇博客中,我们将详细介绍*args和**kwargs,并展…...

微信小程序实现图片转base64
在微信小程序中,图片转base63可以引入第三方插件; 也可以通过下边的方法转base64。 转换方法: imgToBase64(filePath) {return new Promise((resolve, reject) > {let baseFormat data:image/png;base64,let base64 wx.getFileSystem…...

os和os.path模块
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 目录也称文件夹,用于分层保存文件。通过目录可以分门别类地存放文件。我们也可以通过目录快速找到想要的文件。在Python中,并…...
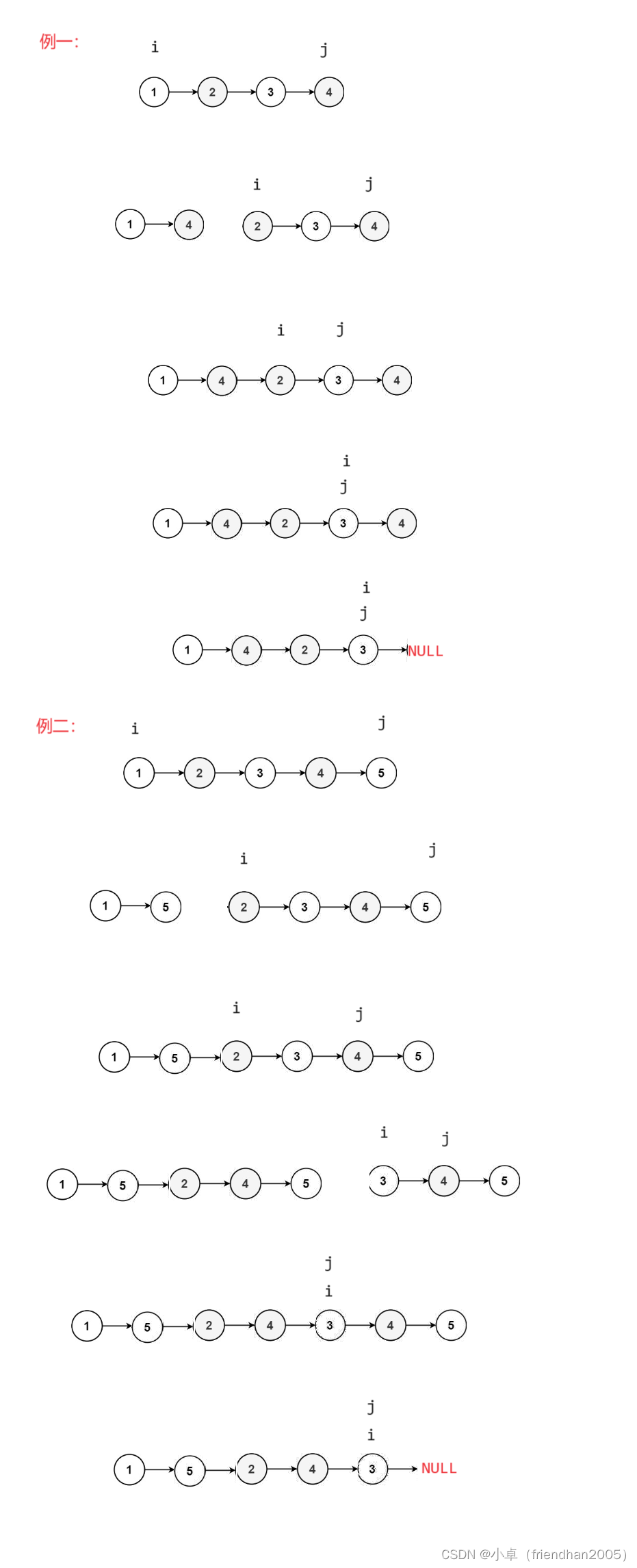
链表题目练习----重排链表
这道题会联系到前面写的一篇文章----快慢指针相关经典问题。 重排链表 指针法 这道题乍一看,好像有点难处理,但如果仔细观察就会发现,这道题是查找中间节点反转链表链表的合并问题,具体细节有些不同,这个在反装中间链…...

【杂记-浅谈XSS跨站脚本攻击】
一、什么是XSS? XSS,Cross-site Scripting,跨站脚本攻击,是一种典型的Web程序漏洞利用攻击,攻击者利用Web程序对用户输入检查不足的漏洞将可执行恶意脚本注入网站或Web应用,当用户访问网页时触发恶意脚本的…...
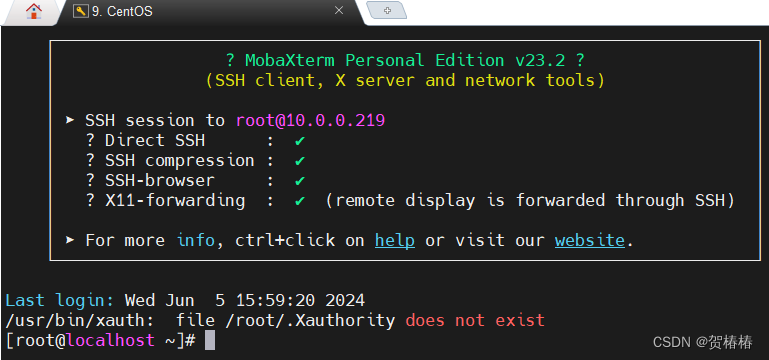
VMware虚拟机与MobaXterm建立远程连接失败
VMware虚拟机与MobaXterm建立远程连接失败 首先可以检查一下是不是虚拟机的ssh服务并不存在 解决方法: 1.更新镜像源 yum -y update 这个过程会有点久,请耐心等待 2.安装ssh yum install openssh-server 3.启动ssh systemctl restart sshd 4.查…...

mysql undolog管理
在MySQL中,Undo Log(撤销日志)用于支持事务的回滚和MVCC(多版本并发控制)。为了避免Undo Log不断增长,影响系统性能,需要进行合理的清理。MySQL的Undo Log清理策略主要依赖于系统的配置参数和后…...

【Linux】进程2——管理概念,进程概念
1.什么是管理? 那在还没有学习进程之前,就问大家,操作系统是怎么管理进行进程管理的呢? 很简单,先把进程描述起来,再把进程组织起来! 我们拿大学为例子 最典型的管理者——校长最典型的被管理…...

【C++】植物大战僵尸杂交版自动存档——防闪退存档消失
植物大战僵尸杂交版现已更新到v2.0.88,闪退问题还是偶有发生,参考网上现有的方案,简单实现了一个。 原理就是监控存档目录的文件变化,一旦有新的存档,则将其备份。如发生闪退,则还原备份即可。 原目录&…...
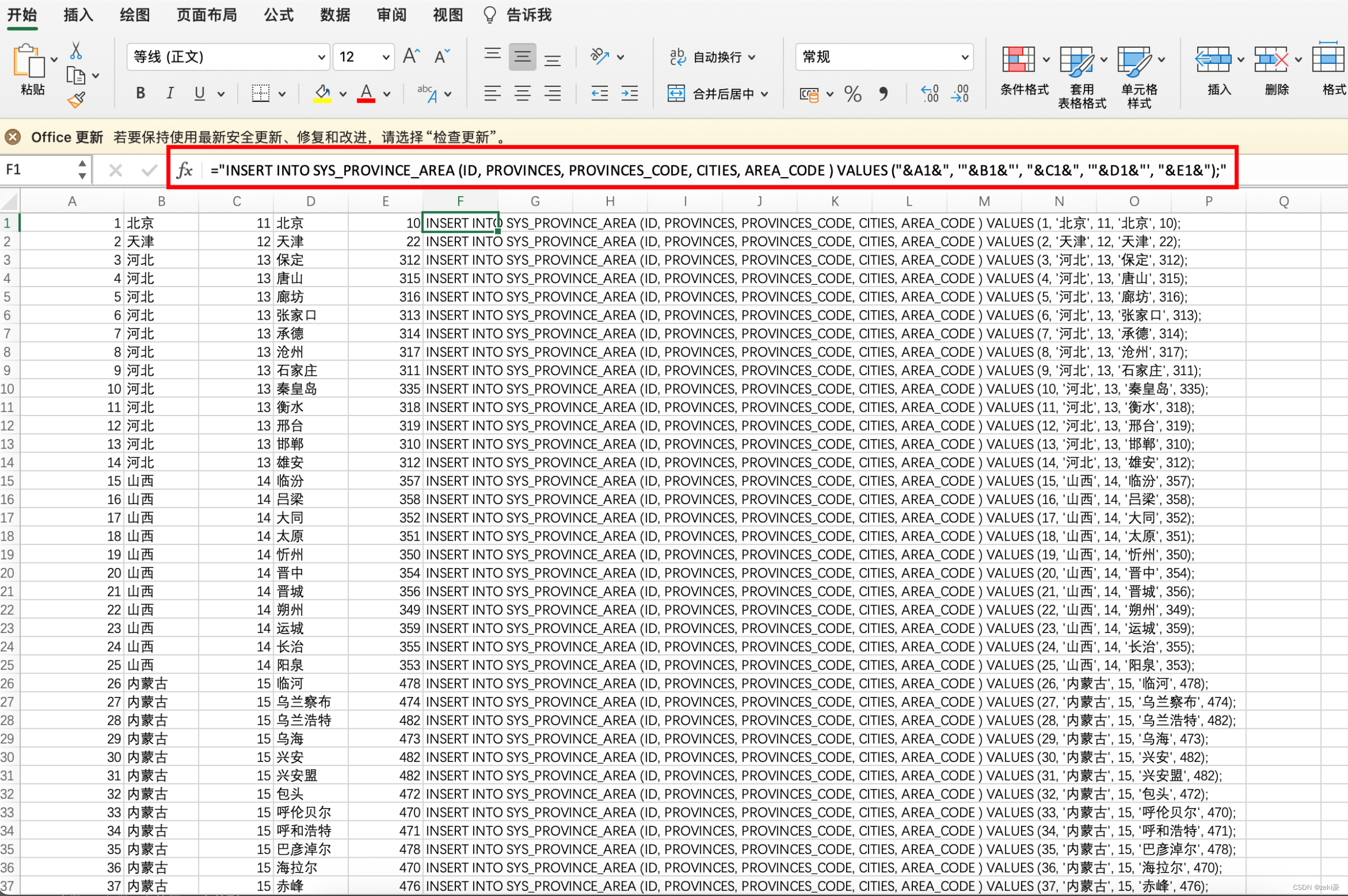
通过Excel,生成sql,将A表数据插入B表
文章目录 投机取巧的方式,进行表数据初始化通过navicat搜索A表数据,然后复制进excel中通过excel的函数方式,将该批量数据自动生成插入B表的sql语句然后一次性拷贝生成的sql语句,放进navicat中一次执行,直接完成数据初始化...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
