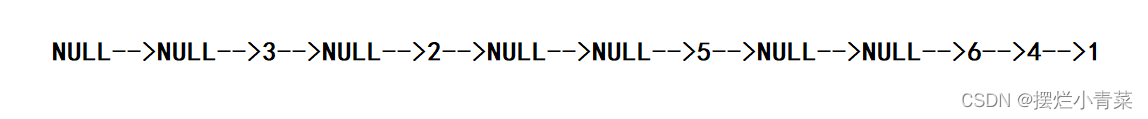数据结构:链式二叉树初阶
目录
一.链式二叉树的逻辑结构
1.链式二叉树的结点结构体定义
2.链式二叉树逻辑结构
二.链式二叉树的遍历算法
1.前序遍历
2.中序遍历
3.后序遍历
4.层序遍历(二叉树非递归遍历算法)
层序遍历概念:
层序遍历算法实现思路:
层序遍历代码实现:
三.链式二叉树遍历算法的运用
1.前序遍历算法的运用
相关练习:
2.后序遍历算法的运用
3.层序遍历算法的运用
问题来源:
四.链式二叉树其他操作接口的实现
1. 计算二叉树结点个数的接口
2.计算二叉树叶子结点的个数的接口
3.计算二叉树第k层结点个数的接口
4.二叉树的结点查找接口(在二叉树中查找值为x的结点)
一.链式二叉树的逻辑结构
1.链式二叉树的结点结构体定义
- 树结点结构体定义:
typedef int BTDataType; typedef struct BinaryTreeNode {BTDataType data; //数据域struct BinaryTreeNode* left; //指向结点左孩子的指针struct BinaryTreeNode* right; //指向结点右孩子的指针 }BTNode;
2.链式二叉树逻辑结构
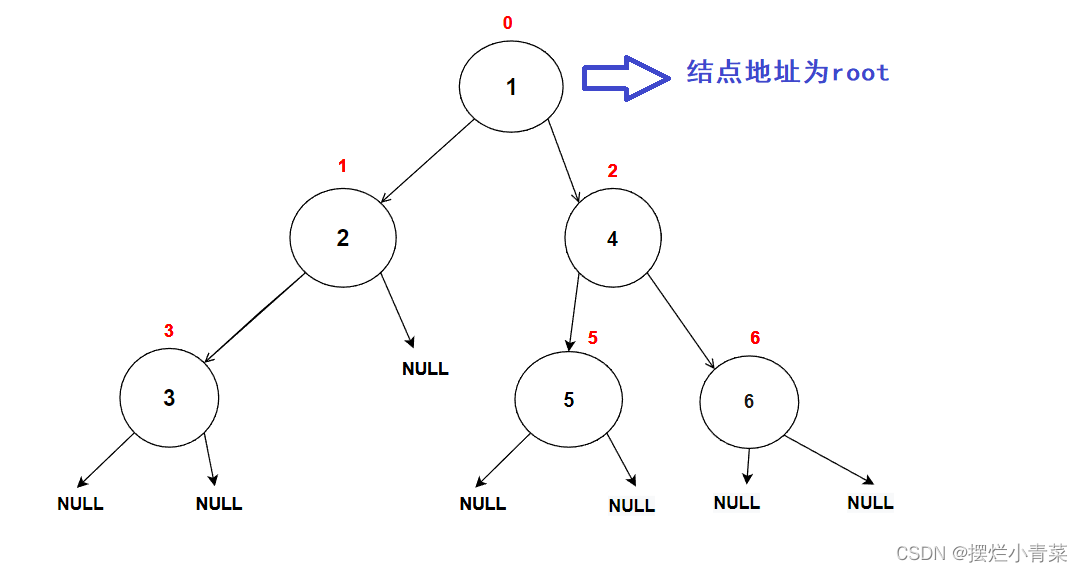
- 这里先暴力"创建"一颗二叉树:
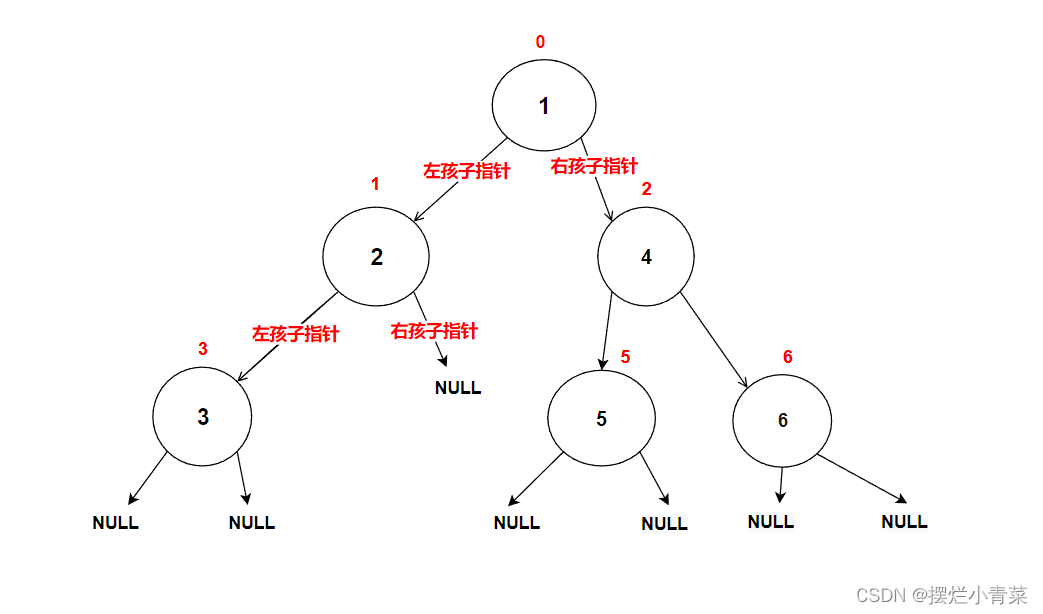
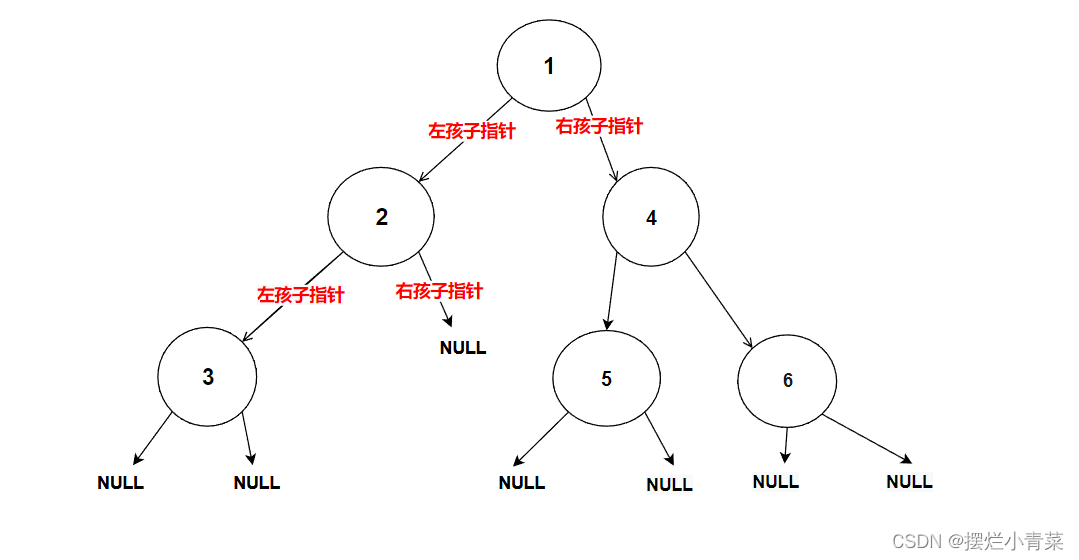
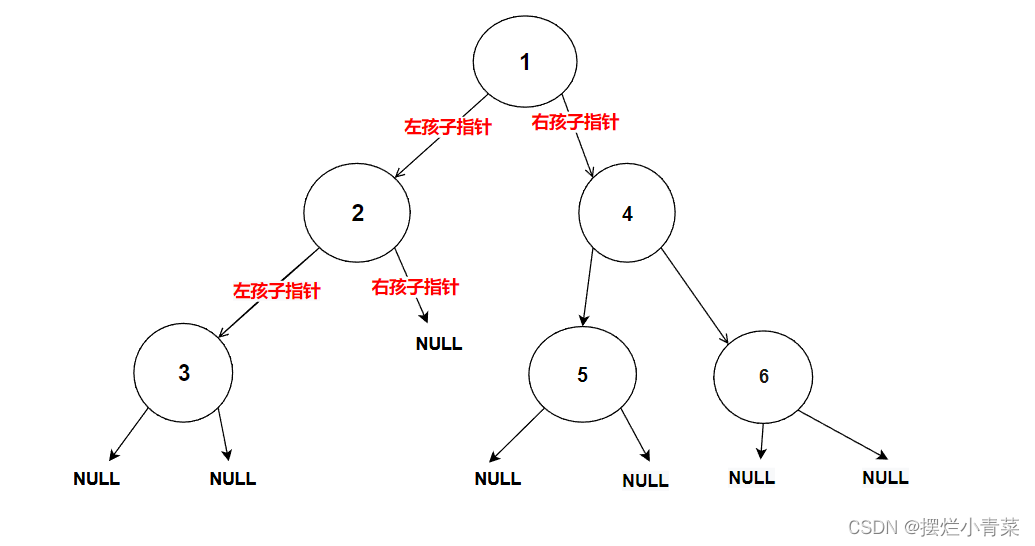
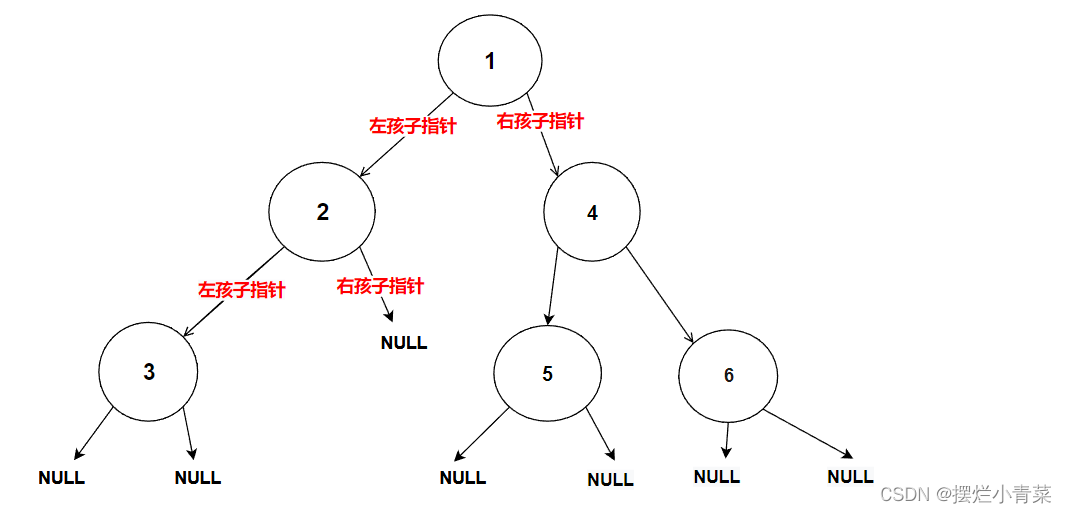
//在内存堆区上申请结点的接口 BTNode* BuyNode( BTDataType x) {BTNode* tem = (BTNode*)malloc(sizeof(BTNode));assert(tem);tem->data = x;tem->left = NULL;tem->right = NULL;return tem; }int main () {BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;//其他操作return 0; }树的逻辑结构图示:
每个树结点都有其左子树和右子树
因此关于链式二叉树的递归算法的设计思路是:关于树T的问题可以分解为其左子树和右子树的问题,树T的左子树和右子树的问题又可以以同样的方式进行分解,因此就形成了递归
关于链式二叉树递归算法的核心思维:左右子树分治思维。
二.链式二叉树的遍历算法
遍历二叉树的递归框架:
- 函数的抽象意义是完成整棵树的遍历
- 为了完成整棵树的遍历我们先要完成该树的左子树的遍历和右子树的遍历
- 左子树和右子树的遍历又可以以相同的方式进行问题拆分,于是便形成了递归(数学上的递推迭代)
//递归遍历二叉树的基本函数结构 void Order(BTNode* root) {if (NULL == root){return;}对当前结点进行某种处理的语句位置1(前序);Order(root->left); //遍历左子树的递归语句对当前结点进行某种处理的语句位置2(中序);Order(root->right); //遍历右子树的递归语句对当前结点进行某种处理的语句位置3(后序); }
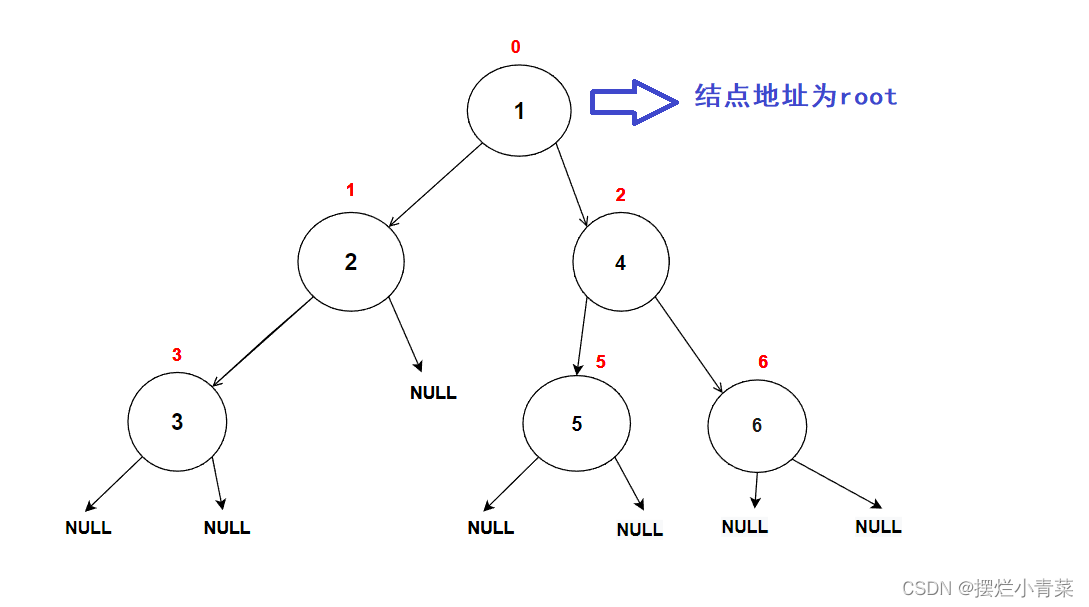
- 通过这个递归函数,我们可以遍历二叉树的每一个结点:(假设根结点的地址为root)
- 根据函数中对当前的root结点进行某种处理的代码语句的位置可将遍历二叉树的方式分为前序遍历(位置1),中序遍历(位置2),后序遍历(位置3)三种
1.前序遍历
//二叉树前序遍历 void PreOrder(BTNode* root) {if (NULL == root){printf("NULL->");//为了方便观察我们将空结点打印出来return;}printf("%d->", root->data); //当前结点处理语句PreOrder(root->left); //向左子树递归PreOrder(root->right); //向右子树递归 }
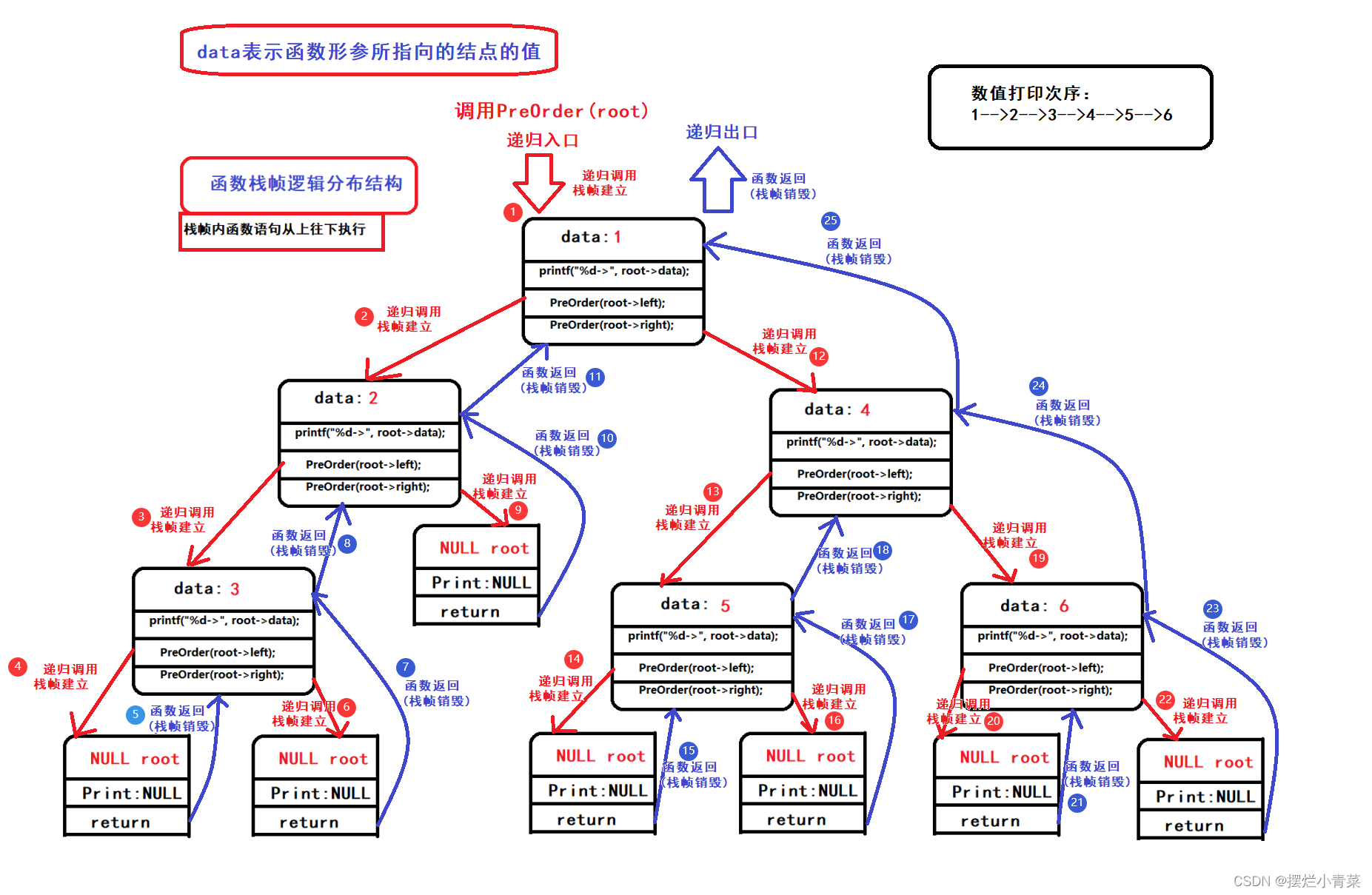
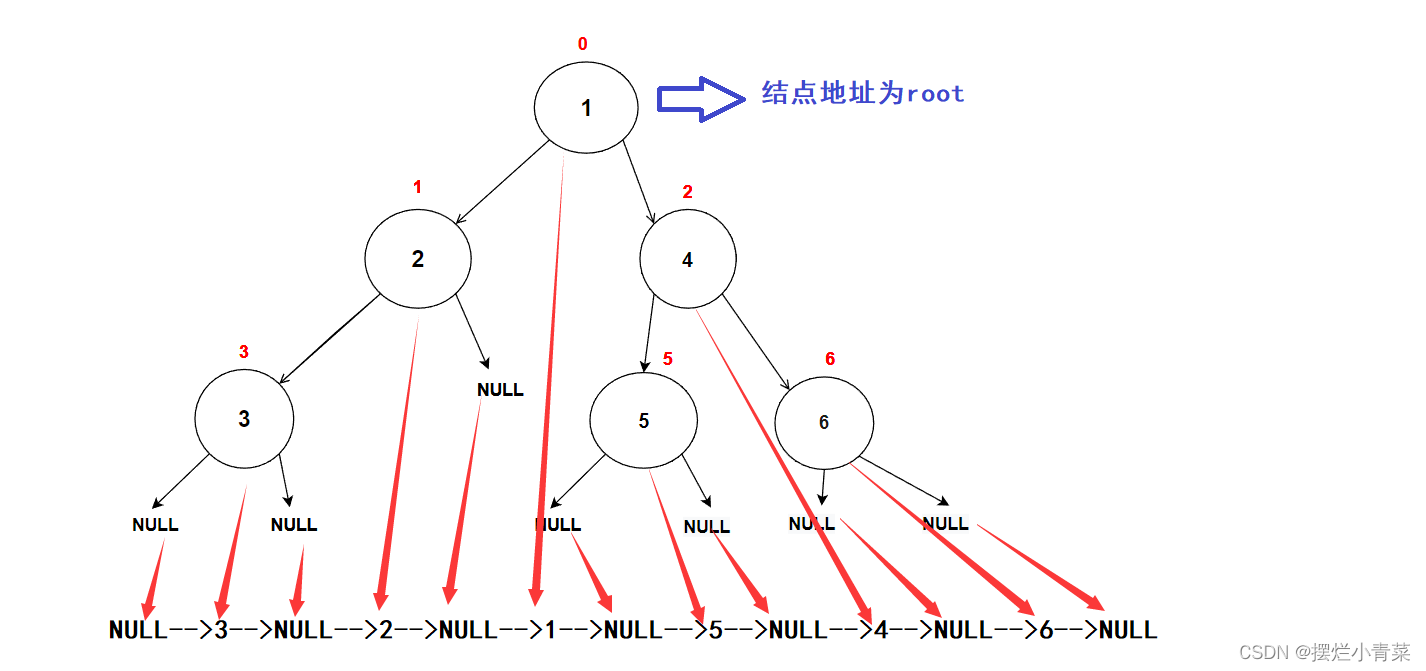
- 以图中的树为例调用前序遍历函数:
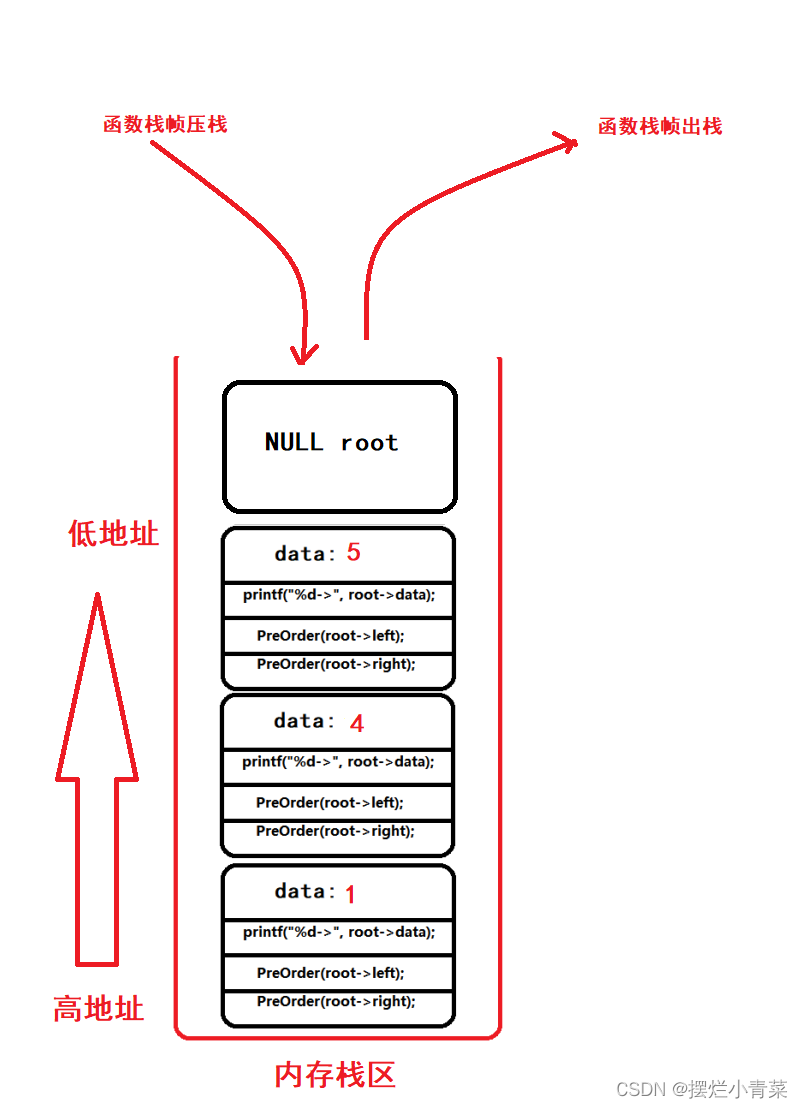
PreOrder(root); //root为树根地址递归函数执行过程中函数栈帧的逻辑结构分布以及代码语句执行次序图示:
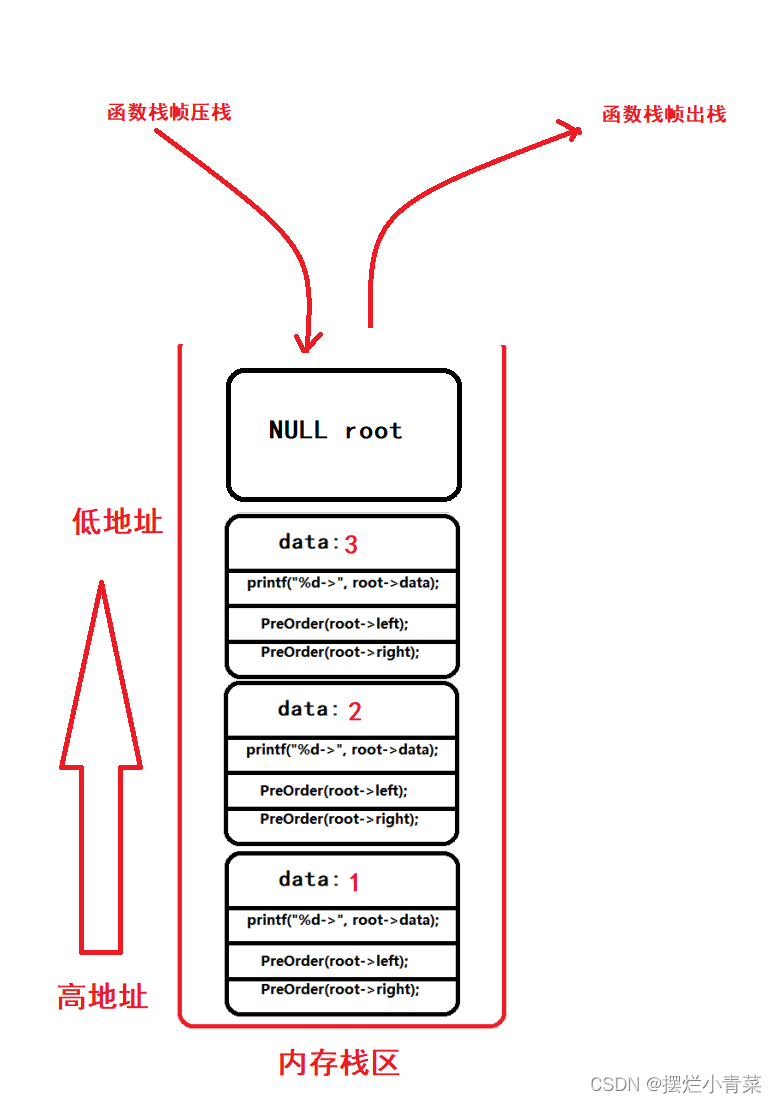
递归函数执行过程中函数栈帧的物理结构分布:
当递归执行到图中的第4步是函数栈帧的物理结构:
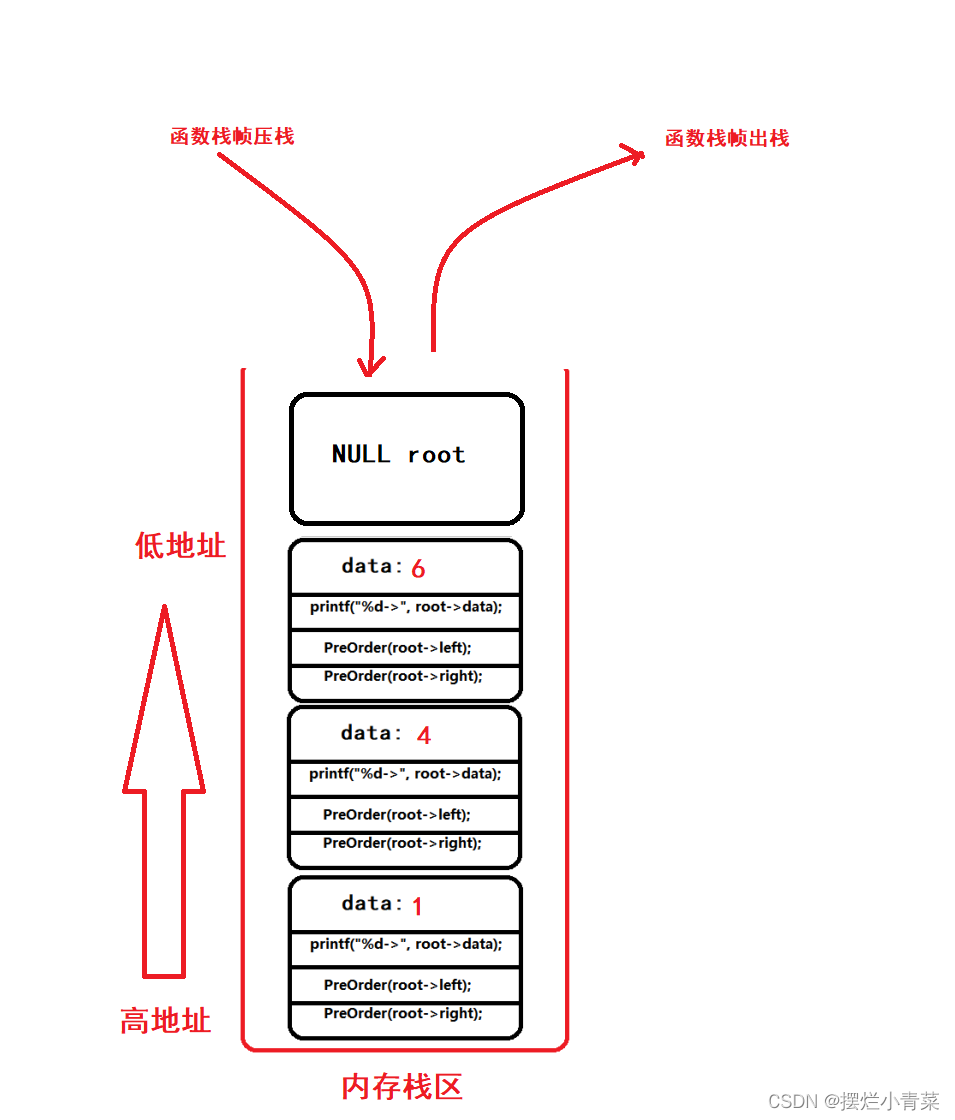
当递归执行到图中的第10步是函数栈帧的物理结构:
当递归执行到图中的第14步是函数栈帧的物理结构:
当递归执行到图中的第22步是函数栈帧的物理结构:
递归函数执行过程中同一时刻开辟的函数栈帧的最大个数取决于树的高度:因此递归遍历二叉树的空间复杂度为:O(logN);
2.中序遍历
//二叉树中序遍历 void InOrder(BTNode* root) {if (NULL == root){printf("NULL->"); //为了方便观察我们打印出空结点return;}InOrder(root->left); //向左子树递归printf("%d->", root->data); //打印结点值(root处理语句)InOrder(root->right); //向右子树递归 }
- 递归函数执行过程分析方法与前序遍历类似
- 对于图中的二叉树,中序遍历的结点值打印次序为:
3.后序遍历
//二叉树后序遍历 void BackOrder(BTNode* root) {if (NULL == root){printf("NULL->"); //为了方便观察我们打印出空结点return;}BackOrder(root->left); //向左子树递归BackOrder(root->right); //向右子树递归printf("%d->", root->data); //打印结点值(root处理语句) }
- 递归函数执行过程分析方法与前序遍历类似
- 对于图中的二叉树,后序遍历的结点值打印次序为:
4.层序遍历(二叉树非递归遍历算法)
层序遍历概念:
二叉树的层序遍历是借助结点指针队列循环实现的二叉树遍历算法
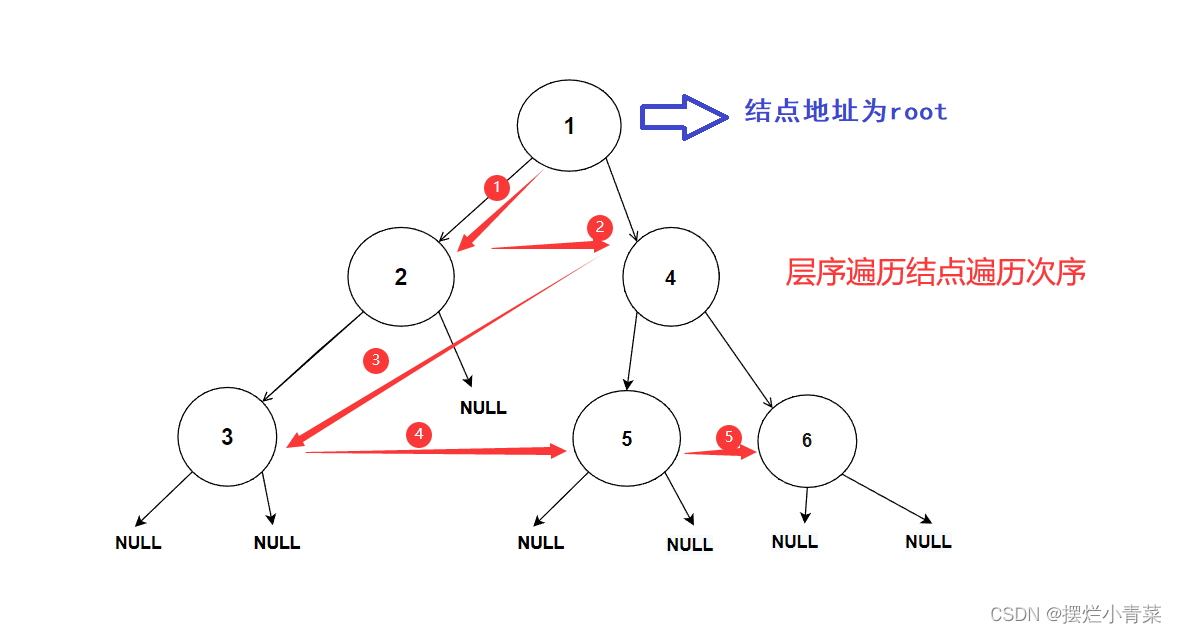
树结点的遍历次序是从低层到高层,同一层从左到右进行遍历的:
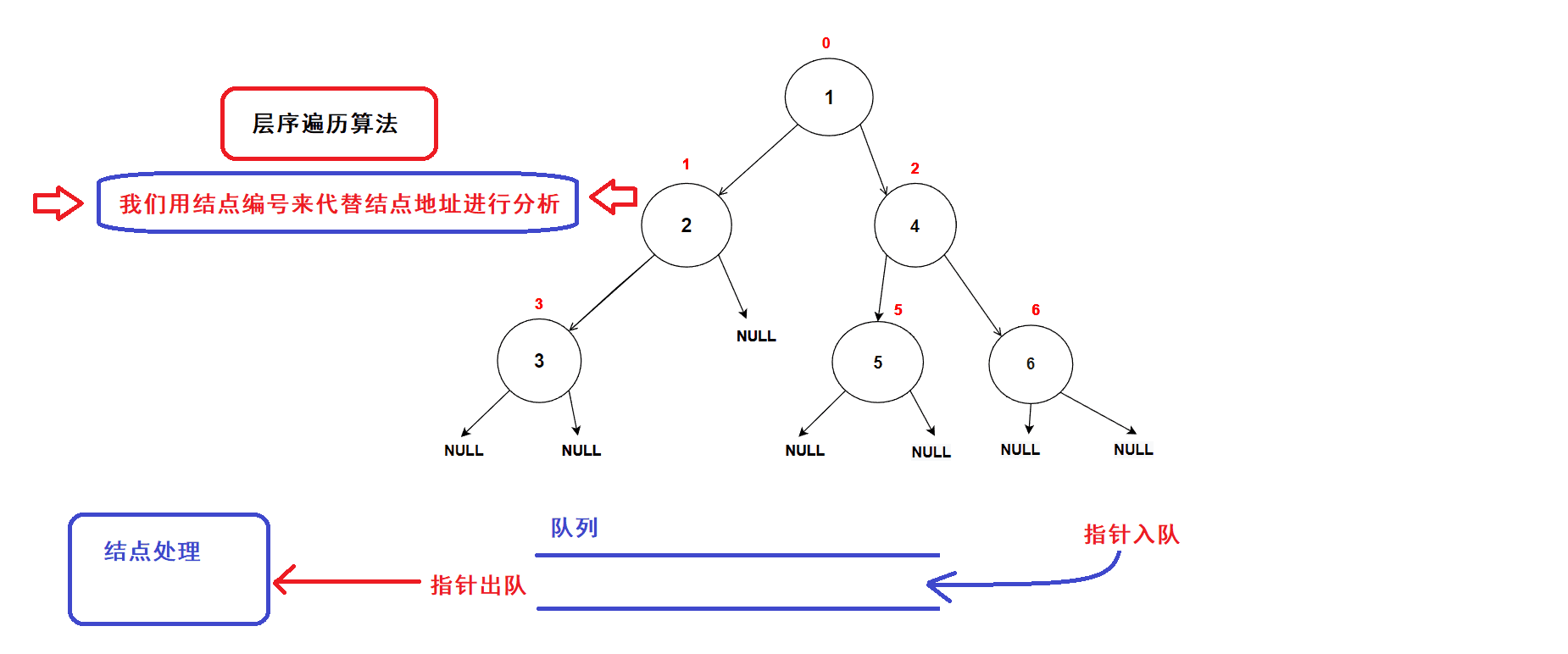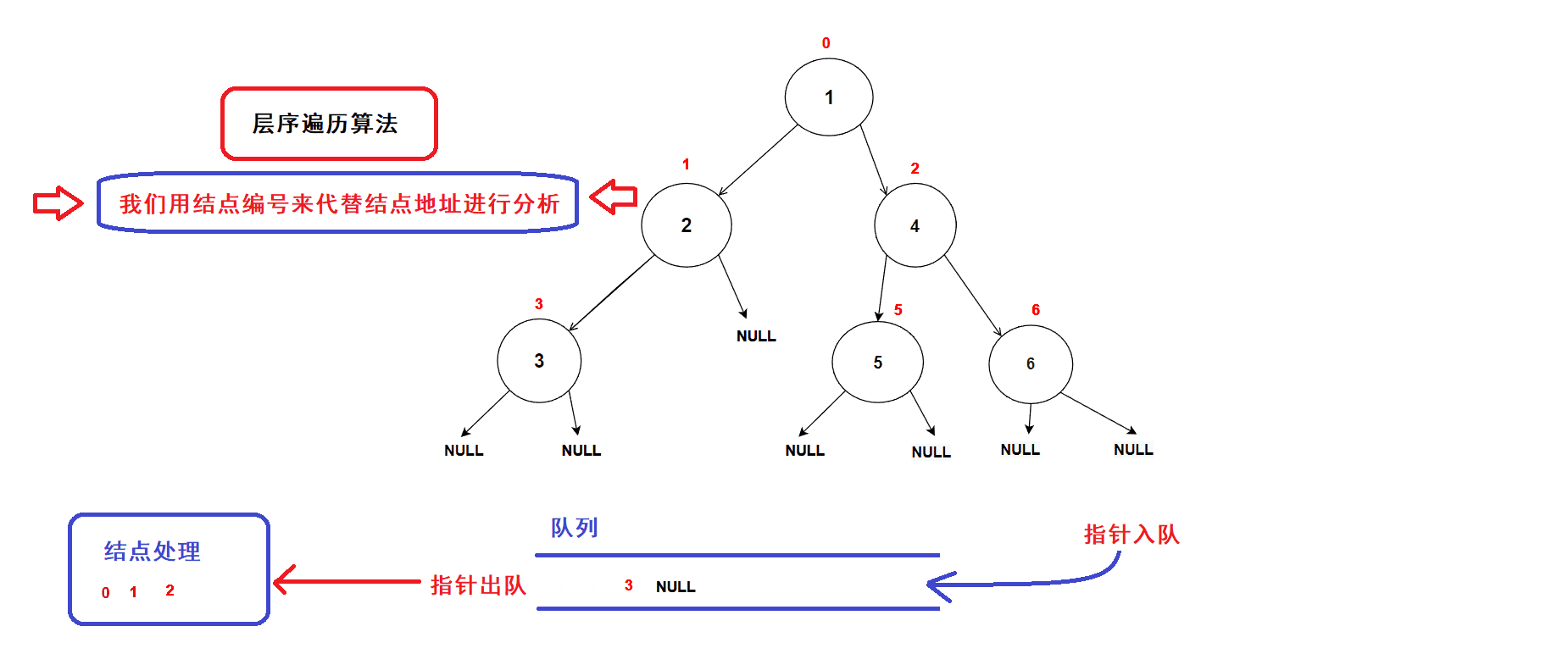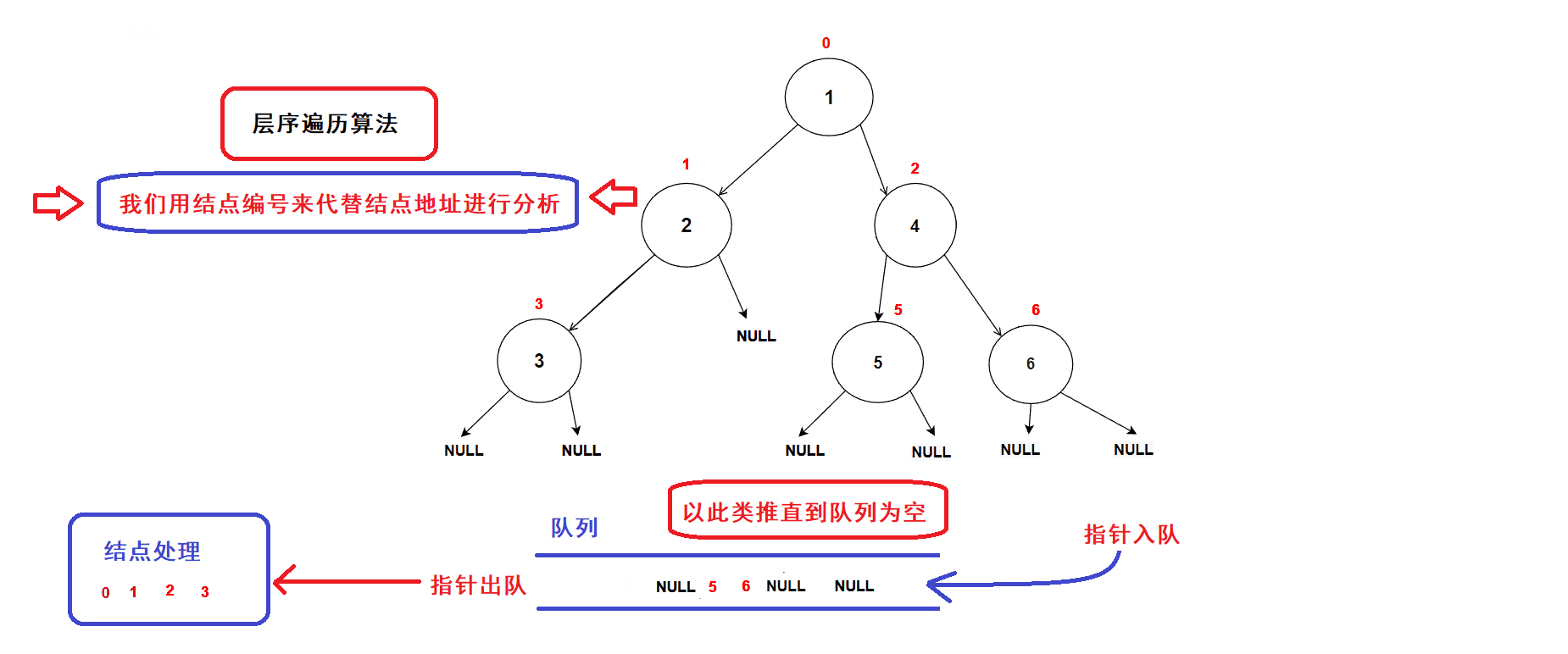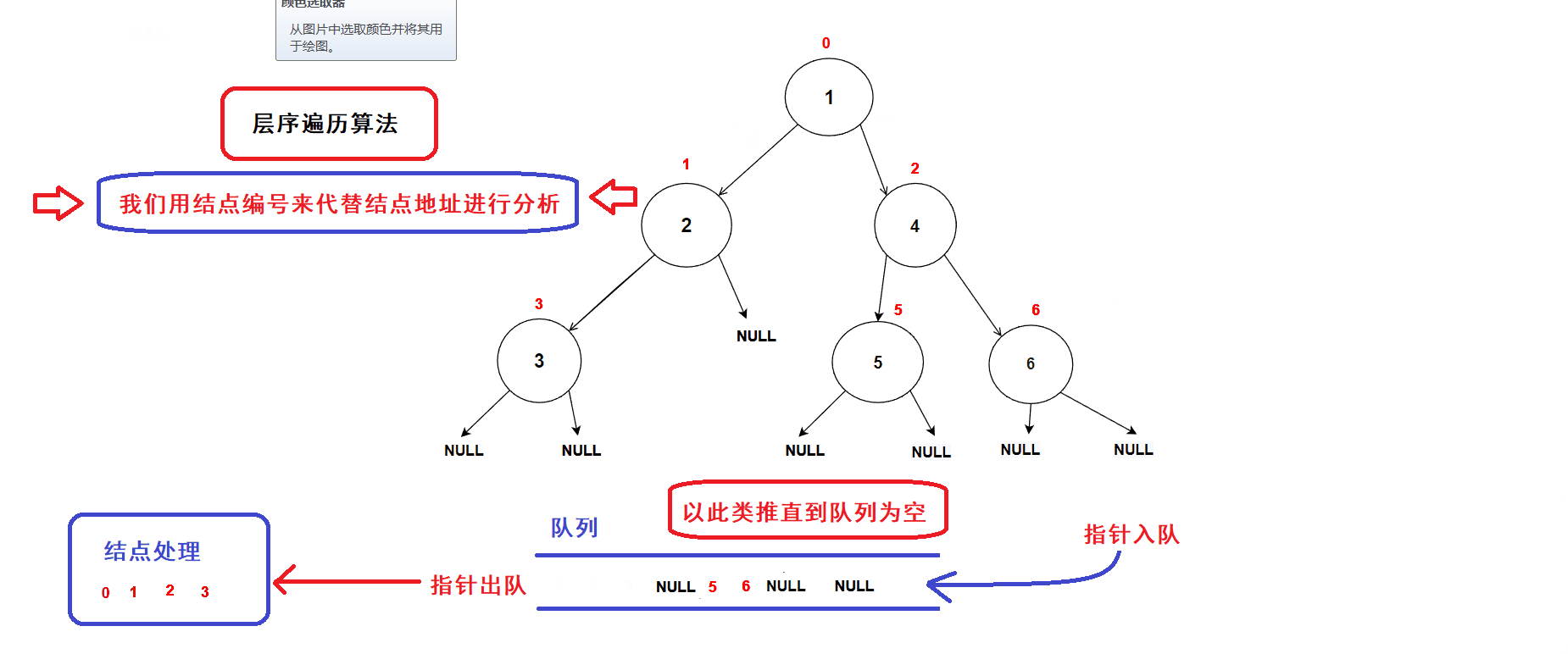
层序遍历算法实现思路:
- 创建一个队列,将树的根结点地址插入队列中;(队列中的数据先进先出,数据从队尾入队从队头出队)
- 接着开始执行循环语句
- 每一次循环,取出队头的一个指针,对其进行处理(打印数值等等处理),若队头指针不为空指针,则将队头指针指向的结点的左右孩子指针插入队列中,重复循环直到队列为空为止.
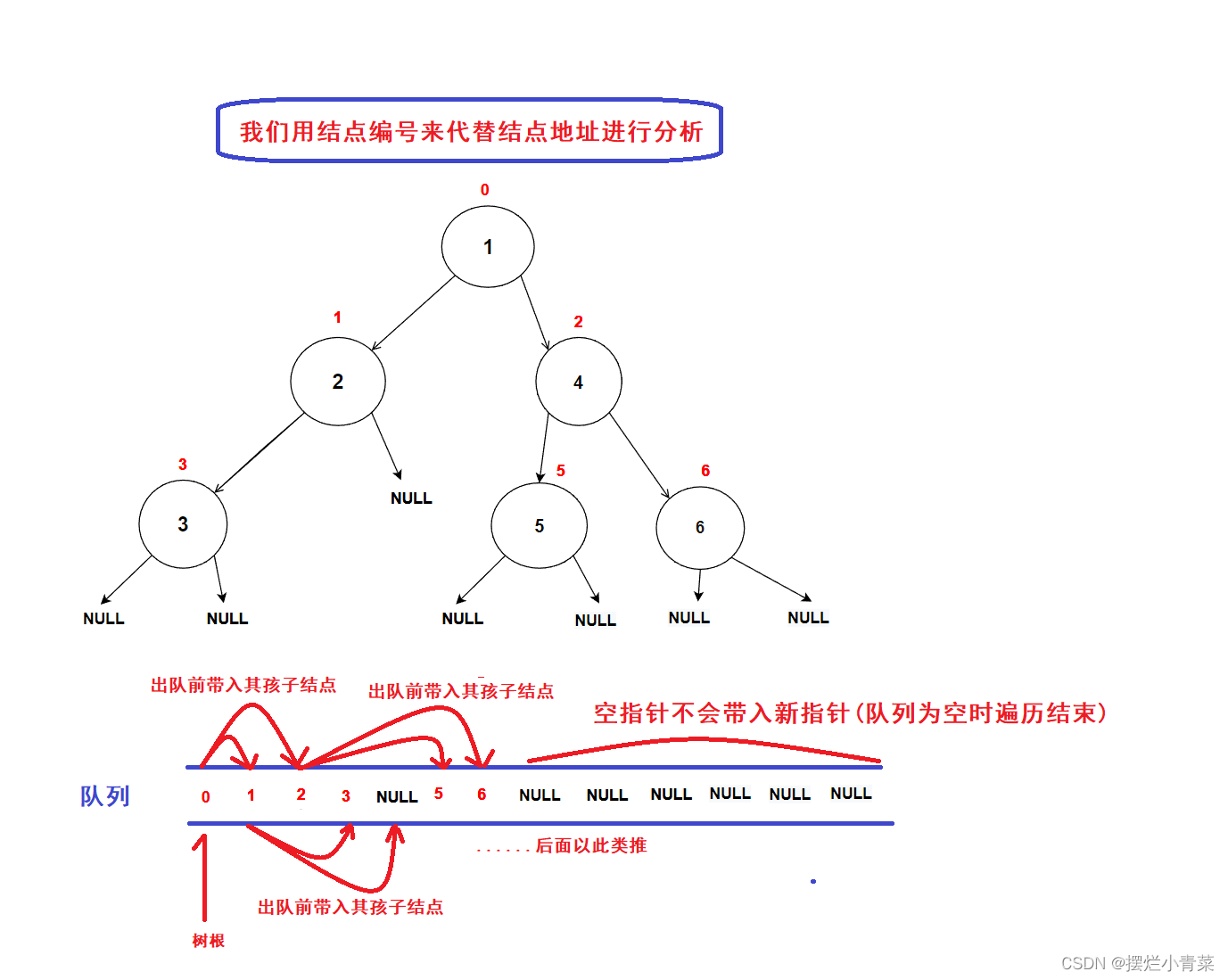
- 树结点指针入队次序图示:
- 经过分析可知:队列中的树结点地址就是按照树结点的层序逻辑顺序进行排列的(从根结点开始,前一层结点指针出队后会带入下一层结点的指针),因此该算法可以完成二叉树的层序遍历
- 算法gif图示:
层序遍历代码实现:
- 为了方便我们直接使用C++STL的queue类模板 (VS2022的queue对象数据入队(尾插)接口为push,数据出队(头删)接口为pop)(不同编译器接口命名可能不同)
- 如果要使用C语言则需要自己手动实现队列
void LevelOrder(BTNode* root) {queue<BTNode*> NodeStore; //创建一个队列用于存储结点指针NodeStore.push(root); //将根结点指针插入队列中while (!NodeStore.empty()) //若队列不为空则循环继续{BTNode* tem = NodeStore.front();//保存队头指针NodeStore.pop(); //队头指针出队if (nullptr != tem){cout << (tem->data)<<' '; //处理出队的结点(这里是打印其结点值)}if (nullptr != tem) //若出队结点不为空,则将其孩子结点指针带入队列{NodeStore.push(tem->left); //将出队结点的左孩子指针带入队列NodeStore.push(tem->right); //将出队结点的右孩子指针带入队列}}cout << endl; }
三.链式二叉树遍历算法的运用
1.前序遍历算法的运用
前序遍历递归:
- 先处理根
- 向左子树递归
- 向右子树递归
- 由于根处理语句在前序递归函数中是首先执行的,因此我们可以利用前序遍历递归框架来实现链式二叉树的递归构建(在前序递归的框架下我们可以实现先创建根结点,再创建根结点的左右子树,中序和后序递归无法完成树的递归构建)
相关练习:
二叉树遍历_牛客题霸_牛客网 (nowcoder.com)
https://www.nowcoder.com/practice/4b91205483694f449f94c179883c1fef?tpId=60&&tqId=29483&rp=1&ru=/activity/oj&qru=/ta/tsing-kaoyan/question-ranking(本题源自清华大学OJ)
问题描述:
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。
例如:先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
(输入的字符串,长度不超过100.)
示例:
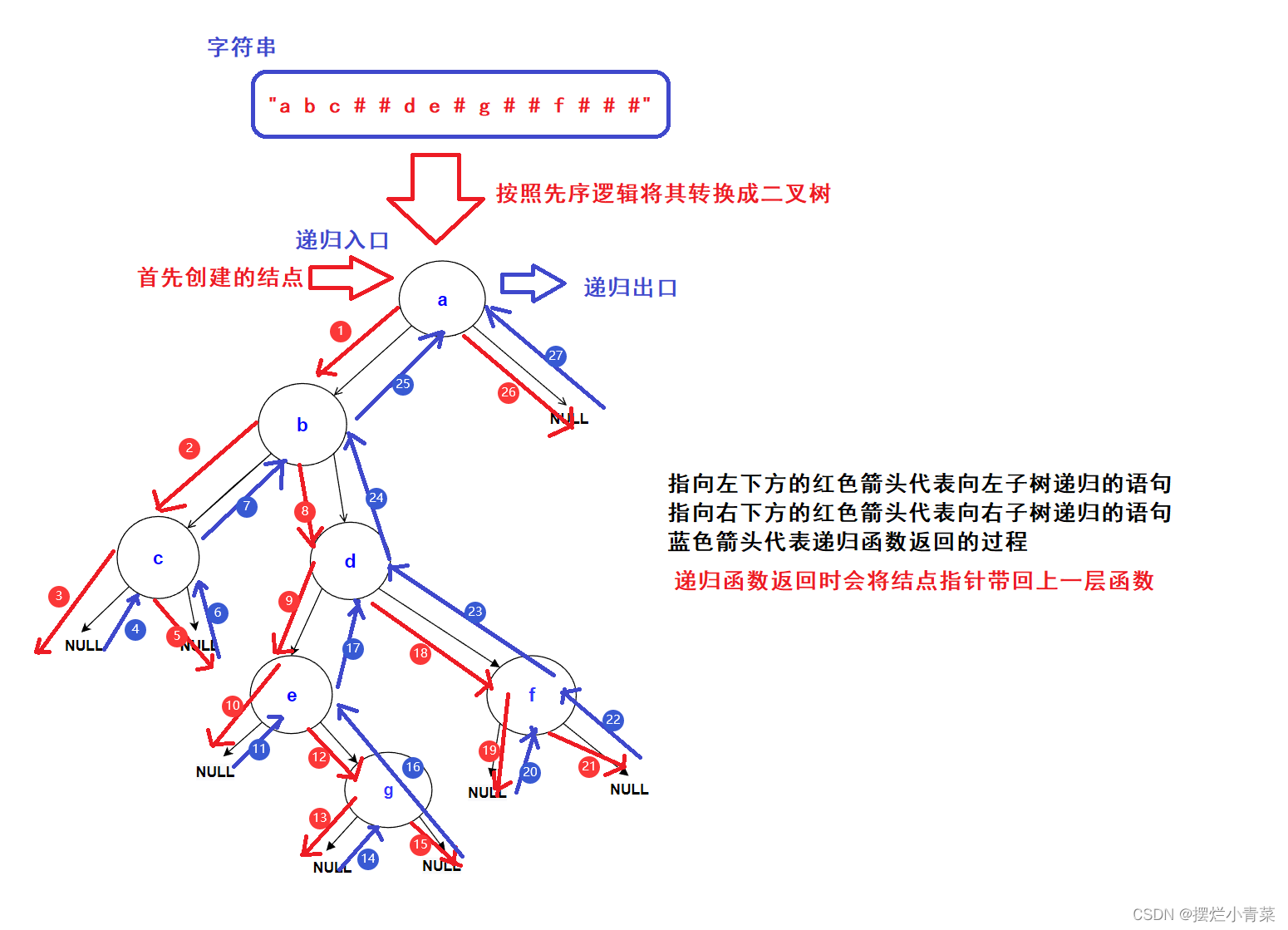
- 输入:abc##de#g##f###
- c b e g d f a
问题分析:
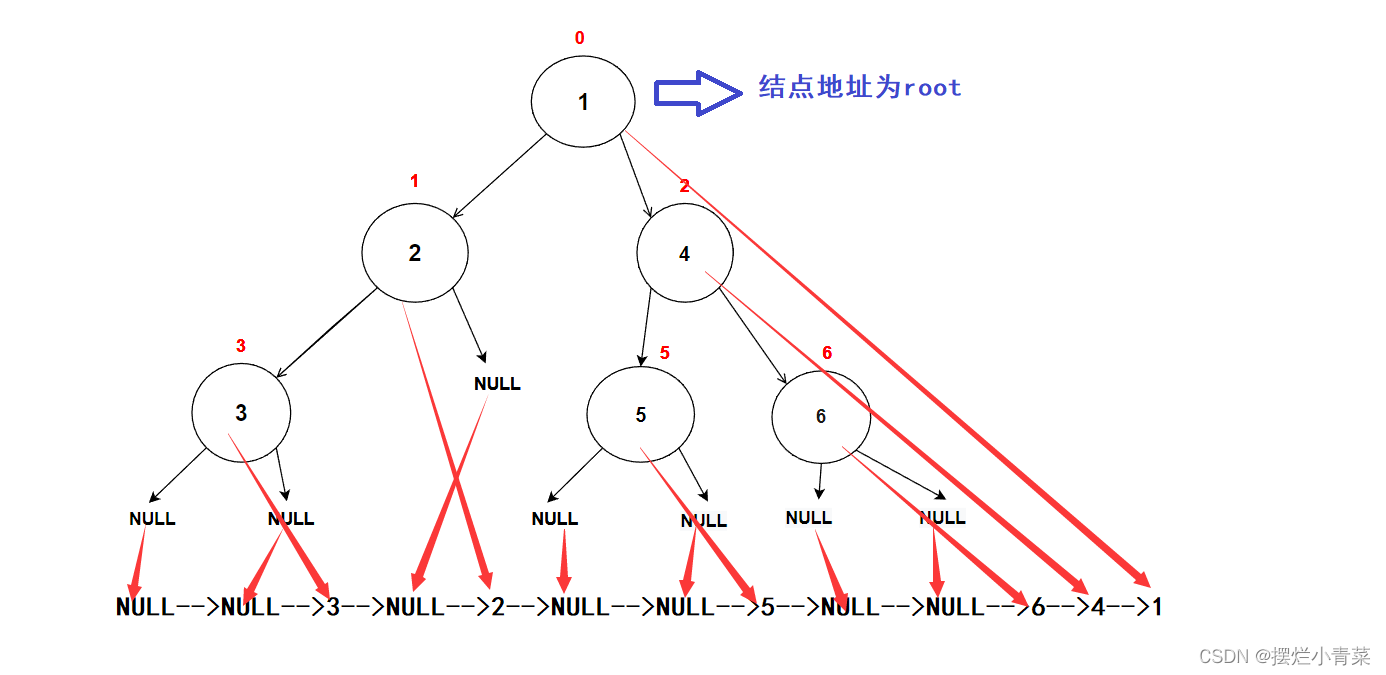
- 以字符串"abc##de#g##f###"为例,先分析一下在先序遍历的逻辑顺序下该字符串所对应的二叉树结构:
如果按照中序逻辑顺序打印这颗树结果为:c-->b-->e-->g-->d-->f-->a;下面给出各个#所代表的空树在树中的逻辑位置:
- 递归构建分析:
- 进一步分析可知:给定的字符串序列必须满足二叉树的前序序列逻辑,不然该字符串序列便无法被转换成一颗完整的二叉树
- 借助递归分析我们可以实现二叉树的递归构建代码
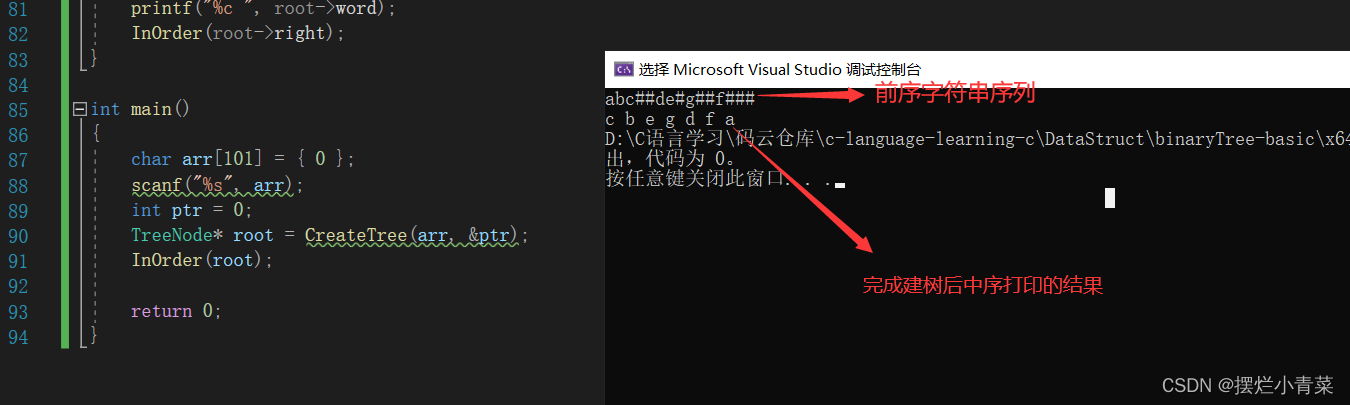
- 为了方便理解, 先给出主函数测试代码,熟悉递归函数的调用方式:
int main() {char arr[101] = {0};scanf("%s",arr); //输入待转换的字符串int ptr = 0; //用于遍历字符串的下标变量TreeNode * root = CreateTree(arr,&ptr); //调用建树函数InOrder(root); //对树进行中序遍历return 0; }建树递归函数首部:
TreeNode * CreateTree(char * input,int* ptr)
input是待转换的字符串的首地址
ptr是用于遍历字符串的下标变量的地址,这里一定要传址,因为我们要在不同的函数栈帧中修改同一个字符数组下标变量
函数实现:
TreeNode * CreateTree(char * input,int* ptr) {if('#'==input[*ptr]) //#代表空树,直接将空指针返回给上层结点即可{++*ptr;return nullptr;}TreeNode * root = new TreeNode; //申请新结点root->word = input[*ptr]; //结点赋值 ++*ptr; //字符数组下标加一处理下一个字符root->left = CreateTree(input,ptr); //向左子树递归root->right = CreateTree(input,ptr);//向右子树递归return root; //将本层结点地址返回给上一层结点(或返回给根指针变量) }整体题解代码:
#include <iostream> #include <string> using namespace std;struct TreeNode //树结点结构体 {char word;TreeNode * left;TreeNode * right; };//ptr是字符串数组下标的地址,这里一定要传址,因为我们要在不同的函数栈帧中修改同一个字符数组下标变量 TreeNode * CreateTree(char * input,int* ptr) {if('#'==input[*ptr]) //#代表空树,直接将空指针返回给上层结点即可{++*ptr;return nullptr;}TreeNode * root = new TreeNode; //申请新结点root->word = input[*ptr]; //结点赋值 ++*ptr; //字符数组下标加一处理下一个字符root->left = CreateTree(input,ptr); //向左子树递归root->right = CreateTree(input,ptr);//向右子树递归return root; //将本层 }void InOrder(TreeNode * root) //中序遍历递归 {if(nullptr == root){return;}InOrder(root->left);printf("%c ",root->word);InOrder(root->right); }int main() {char arr[101] = {0};scanf("%s",arr);int ptr = 0;TreeNode * root = CreateTree(arr,&ptr);InOrder(root);return 0; }
2.后序遍历算法的运用
后序遍历算法:
- 先向左子树递归
- 再向右子树递归
- 完成左右子树的处理后再处理根
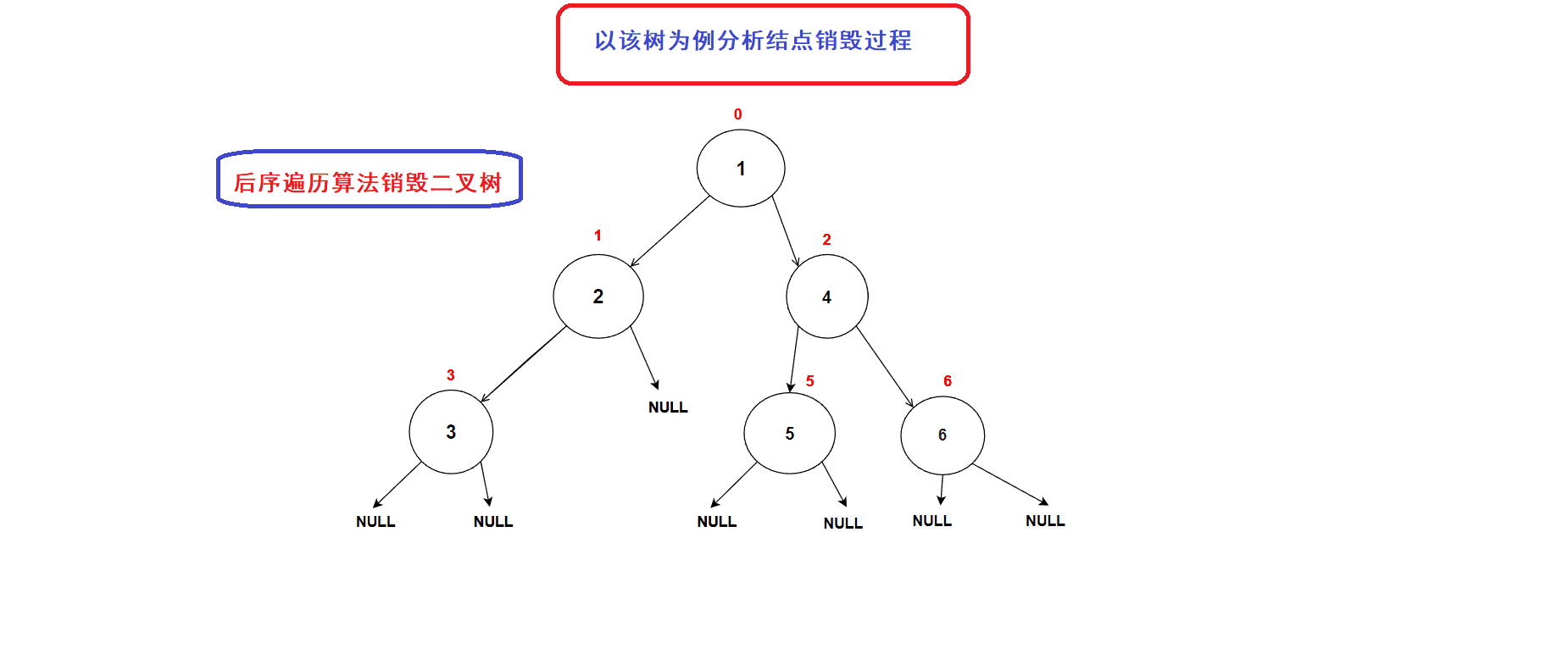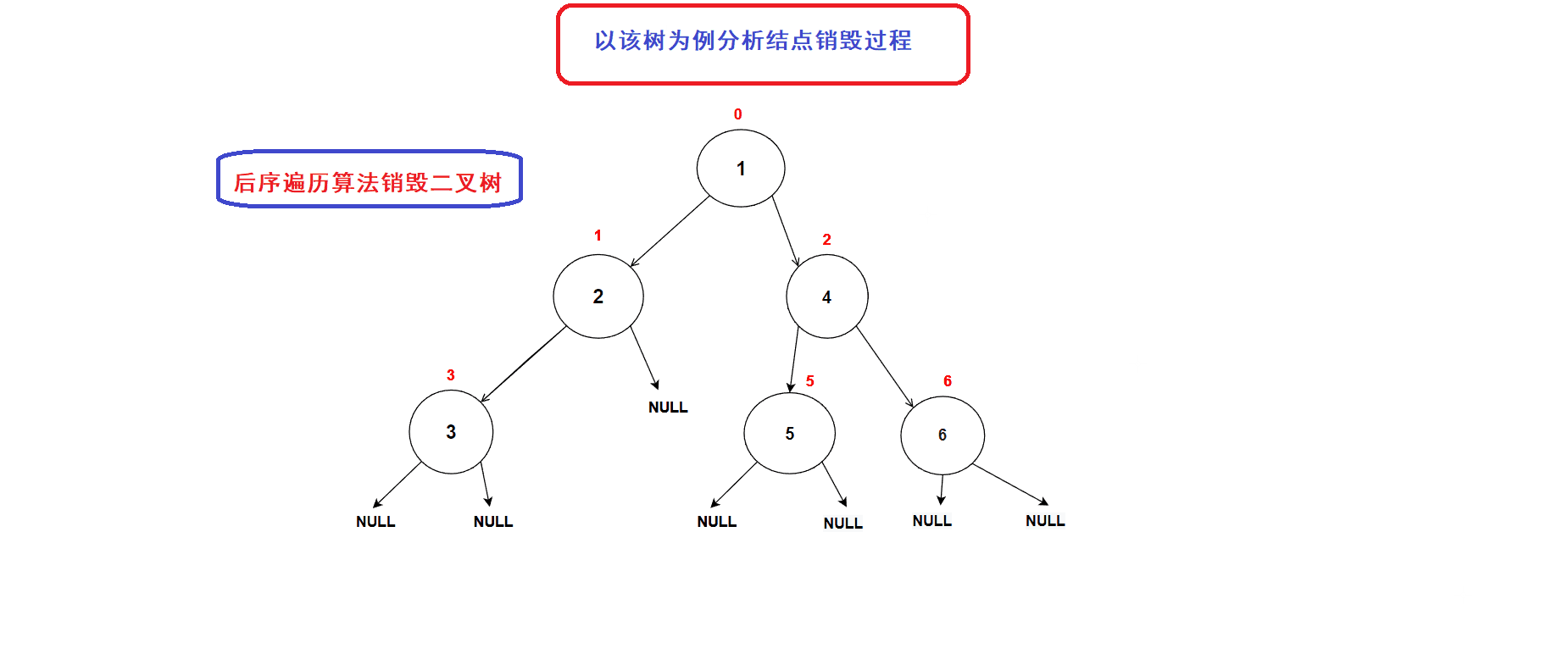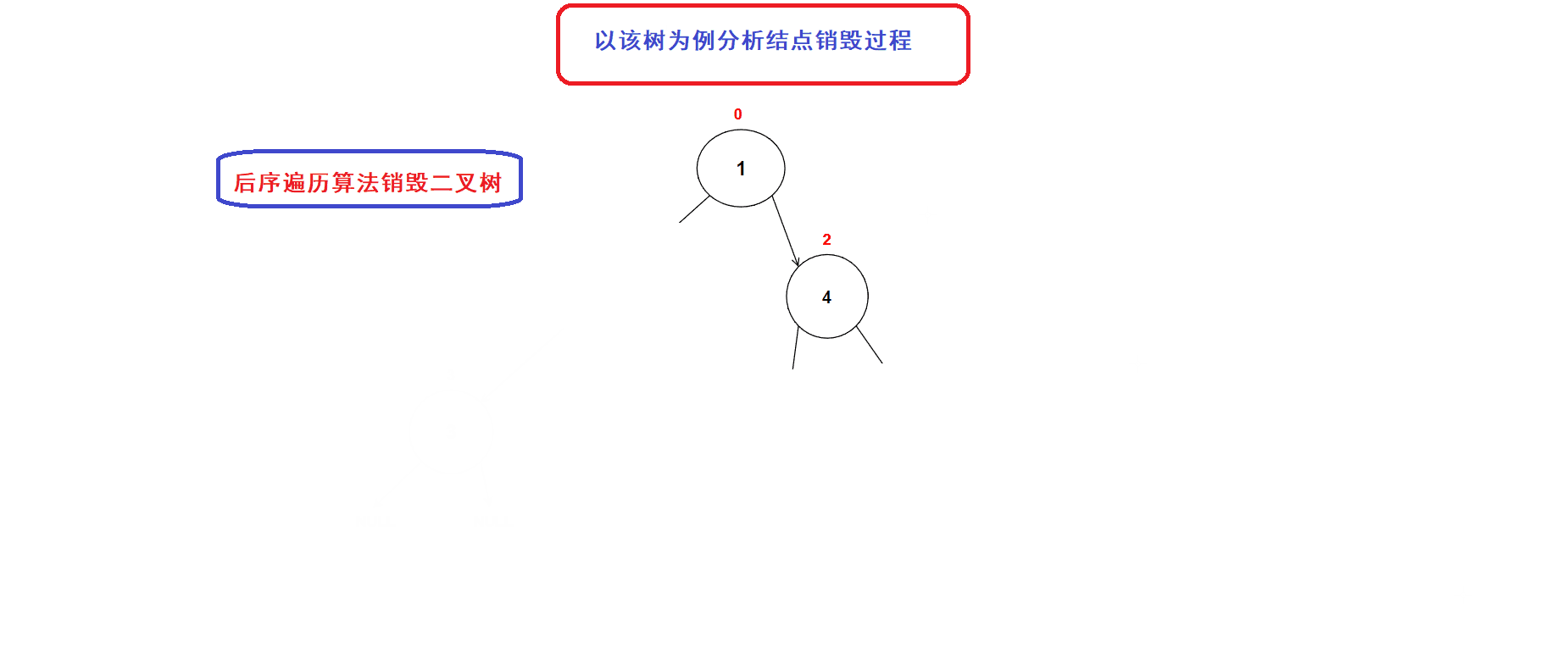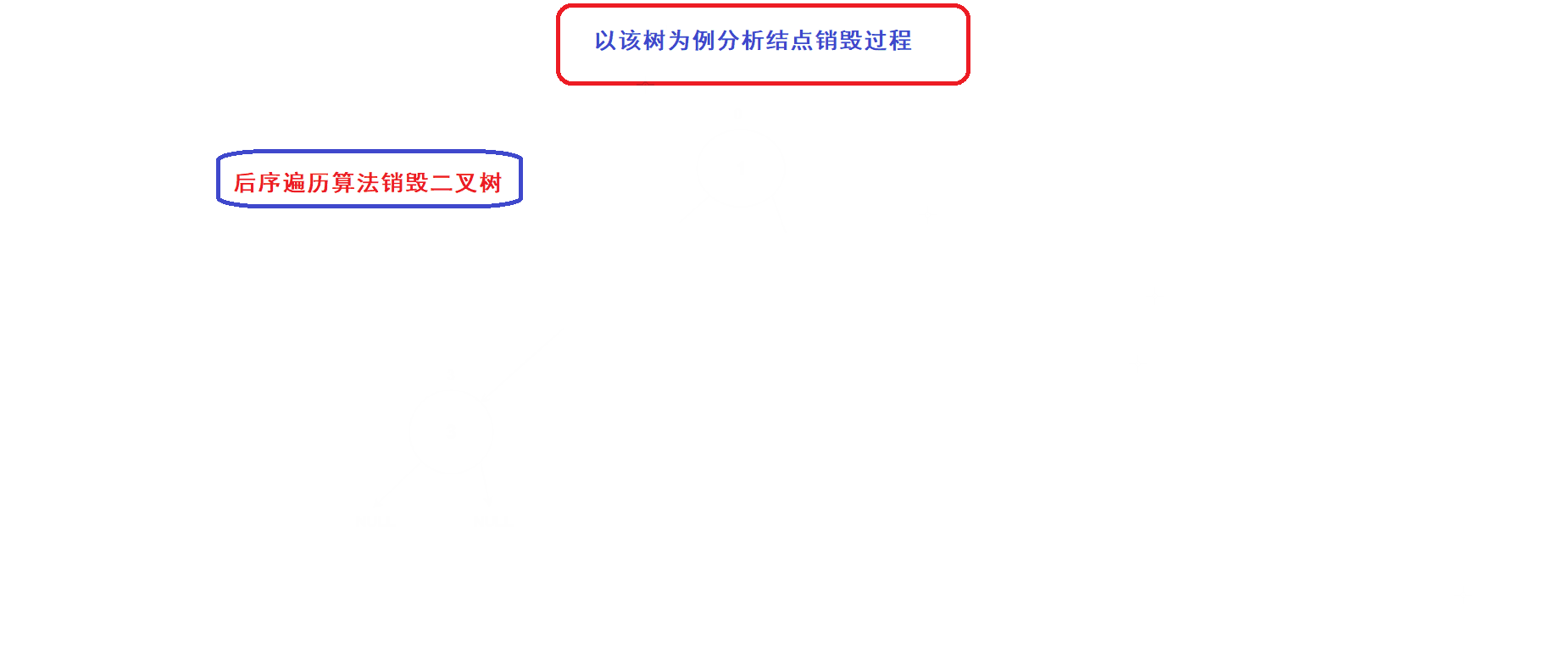
后序遍历算法的思想刚好可以适用于二叉树的销毁过程. (前序和中序算法不能完成二叉树的销毁,因为一旦我们释放了当前结点便无法再向左右子树进行递归(地址丢失))
- 二叉树销毁接口:
// 二叉树销毁 void BinaryTreeDestory(BTNode* root) {if (NULL == root){return;}BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root); //释放到当前结点的内存空间}二叉树销毁过程图示:
3.层序遍历算法的运用
层序遍历算法可以用于检验一颗二叉树是否为完全二叉树;
问题来源:
958. 二叉树的完全性检验 - 力扣(Leetcode)
https://leetcode.cn/problems/check-completeness-of-a-binary-tree/问题描述:
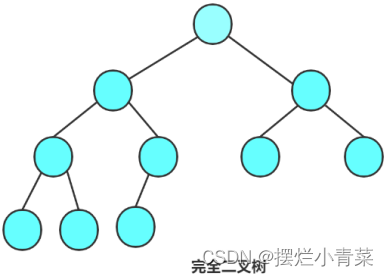
给定一个二叉树的
root,确定它是否是一个完全二叉树 。在一个 完全二叉树中,除了树的最后一层以外,其他层是完全被填满的,并且最后一层中的所有结点都是靠左排列的。
958. 二叉树的完全性检验 - 力扣(Leetcode)
题解接口:
class Solution { public:bool isCompleteTree(TreeNode* root) {} };
关于完全二叉树的结构特点参见青菜的博客:http://t.csdn.cn/6qEro
http://t.csdn.cn/6qEro
问题分析:
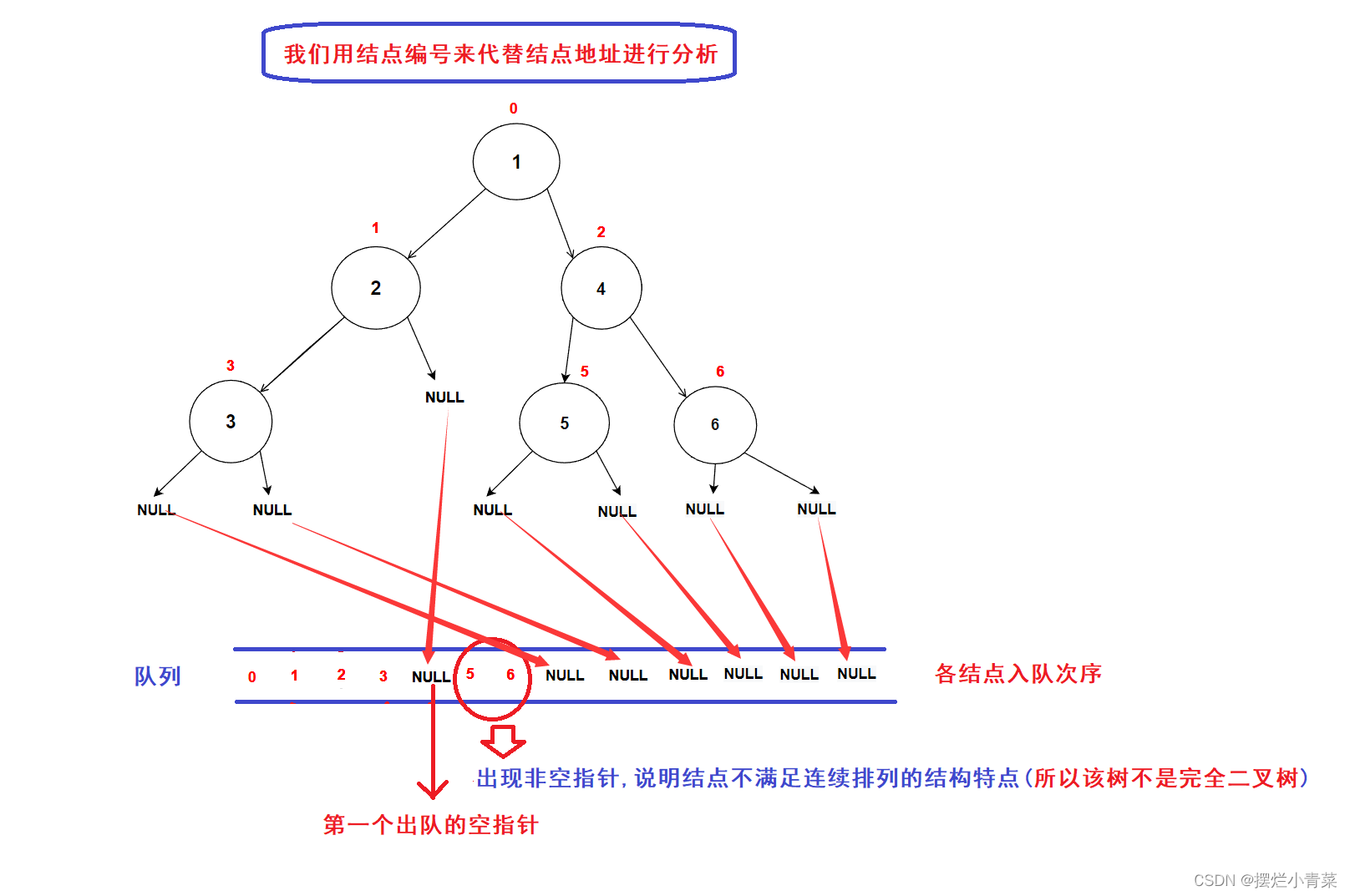
- 完全二叉树的结构特点是各层结点连续排列(各结点编号是连续的)
- 因此层序遍历完全二叉树,各结点指针在队列中都是连续排列的(即各结点指针之间不会出现空指针)
- 根据完全二叉树的结构特点,一旦层序遍历完全二叉树的过程中遍历到了空指针,则说明已经遍历到了二叉树的最后一层
- 我们可以利用层序遍历算法遍历二叉树,当遇到第一个出队的空指针时,检验后续出队的指针中是否还存在非空结点指针,如果后续出队的指针中存在非空指针则说明该树不是完全二叉树,否则说明该树是一颗完全二叉树。
- 算法图示:
题解代码:
class Solution { public:bool isCompleteTree(TreeNode* root) {queue<TreeNode*> ans;ans.push(root); //将根结点指针插入队列while(!ans.empty()) //队列不为空则循环继续{TreeNode* tem = ans.front();ans.pop(); //取出队头指针存入tem变量中if(nullptr == tem) //遇到第一个出队的空指针,停止循环进行下一步判断{break;}else{ans.push(tem->left); //将出队指针的孩子结点指针带入队列ans.push(tem->right);}}while(!ans.empty()){TreeNode* tem = ans.front();ans.pop(); //取出队头指针存入tem变量中if(nullptr != tem) //第一个出队的空指针后续存在非空结点指针,说明该树不是完全二叉树{return false;}}return true; //所有结点指针完成入队出队则验证了该树是完全二叉树} };
四.链式二叉树其他操作接口的实现
链式二叉树的众多递归接口都是通过左右子树分治递归的思想来实现的
树结点结构体定义:
typedef int BTDataType; typedef struct BinaryTreeNode {BTDataType data; //数据域struct BinaryTreeNode* left; //指向结点左孩子的指针struct BinaryTreeNode* right; //指向结点右孩子的指针 }BTNode;
1. 计算二叉树结点个数的接口
函数首部:
int BinaryTreeSize(BTNode* root)
- 将接口函数抽象为某颗树的结点个数A(T)
- 抽象出递推公式: A(T) = A(T->right) + A(T->left) + 1;
- 递推公式的含义是: 树T的结点总个数 = 树T左子树的结点总个数 + 树T右子树的结点总个数 + 1个树T的树根(本质上是左右子树分治思想)
- 由此可以设计出递归函数:
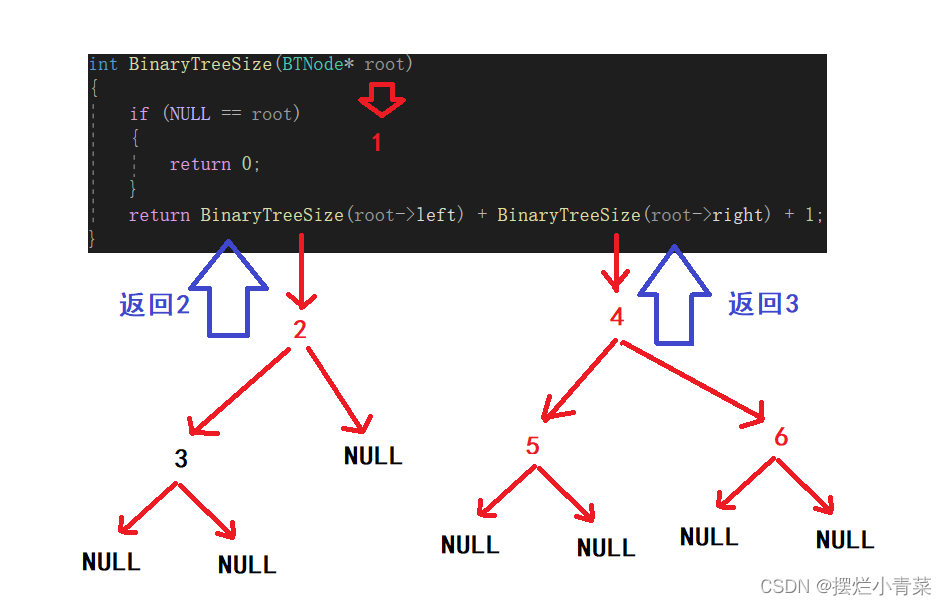
int BinaryTreeSize(BTNode* root) {//空树则返回0if (NULL == root){return 0;}//化为子问题进行分治return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1; }将下图中的树的根结点地址传入递归函数:
递归函数执行过程的简单图示:
2.计算二叉树叶子结点的个数的接口
函数首部:
int BinaryTreeLeafSize(BTNode* root)
- 将接口函数抽象为某颗树的叶子结点的个数A(T)
- 可以抽象出递推公式:A(T) = A(T->left) + A(T->right)
- 递推公式的含义是: 树T的叶子总数 = T的左子树的叶子总数 + T的右子树的叶子总数
- 由此可以设计出递归函数:
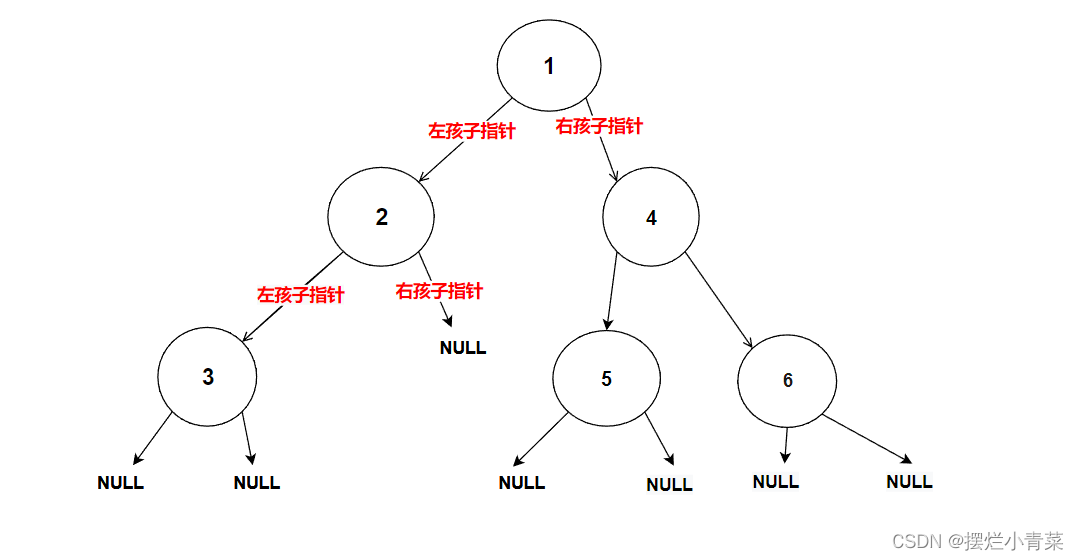
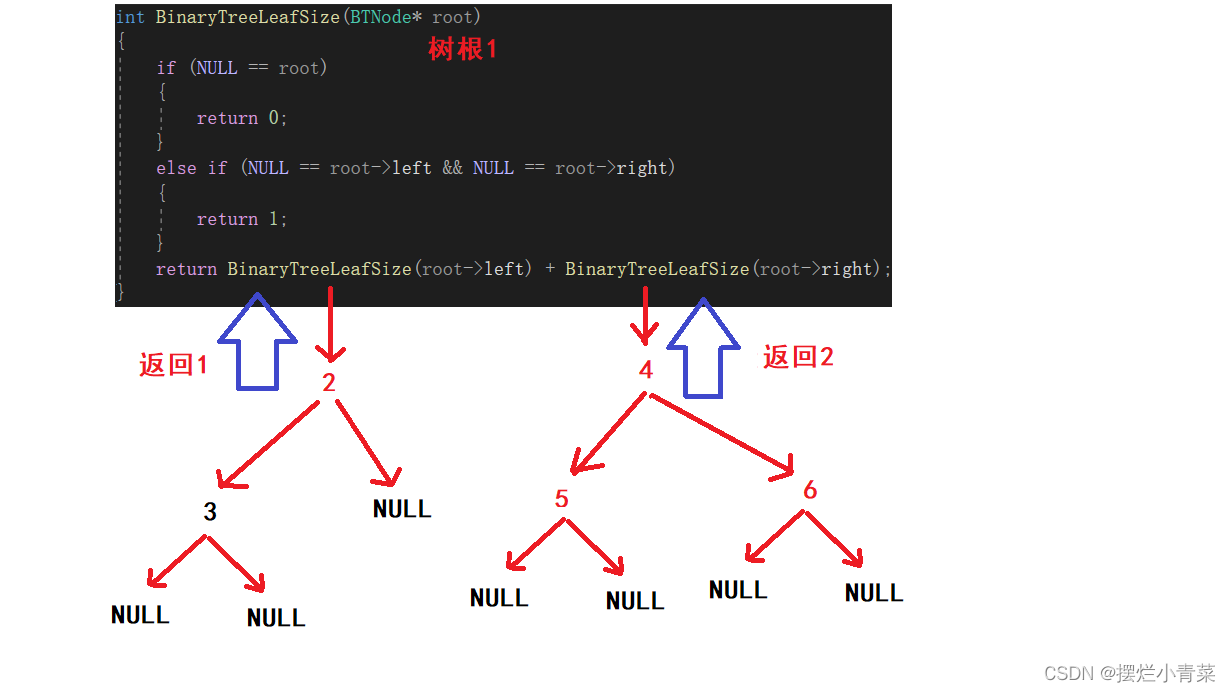
int BinaryTreeLeafSize(BTNode* root) {if (NULL == root) //空树不计入个数{return 0;}else if (NULL == root->left && NULL == root->right) //判断当前树是否为树叶(是树叶则返回1,计入叶子结点个数){return 1;}//化为子问题进行分治return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right); }将下图中的树的根结点地址传入递归函数:
递归函数执行过程的简单图示:
3.计算二叉树第k层结点个数的接口
函数首部:
int BinaryTreeLevelKSize(BTNode* root, int k)
- 将接口函数抽象为某颗树的第k层结点个数A(T,k)
- 可以抽象出递推公式: A(T,k) = A(T->left,k-1) + A(T->right,k-1)
- 递推公式的含义是: 树T的第k层结点个数 = 树T左子树的第k-1层结点数 + 树T右子树的第k-1层结点数
- 由此可以设计出递归函数:
int BinaryTreeLevelKSize(BTNode* root, int k) {assert(k >= 1);//树为空返回0if (NULL == root){return 0;}else if (root && k == 1) //问题分解到求子树的第一层结点(即求树根的个数,树根的个数为1){return 1;}else{return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);} }将下图中的树的根结点地址传入递归函数:
递归函数执行过程的简单图示:
4.二叉树的结点查找接口(在二叉树中查找值为x的结点)
函数首部:
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)递归的思路:
- 若当前树不为空树(若为空树则直接返回空指针),先判断树根是不是要找的结点
- 若树根不是要找的结点,则往左子树递归查找
- 若左子树找不到最后再往右子树递归查找
- 若最后左右子树中都找不到待找结点则返回空指针
- 设计递归函数:
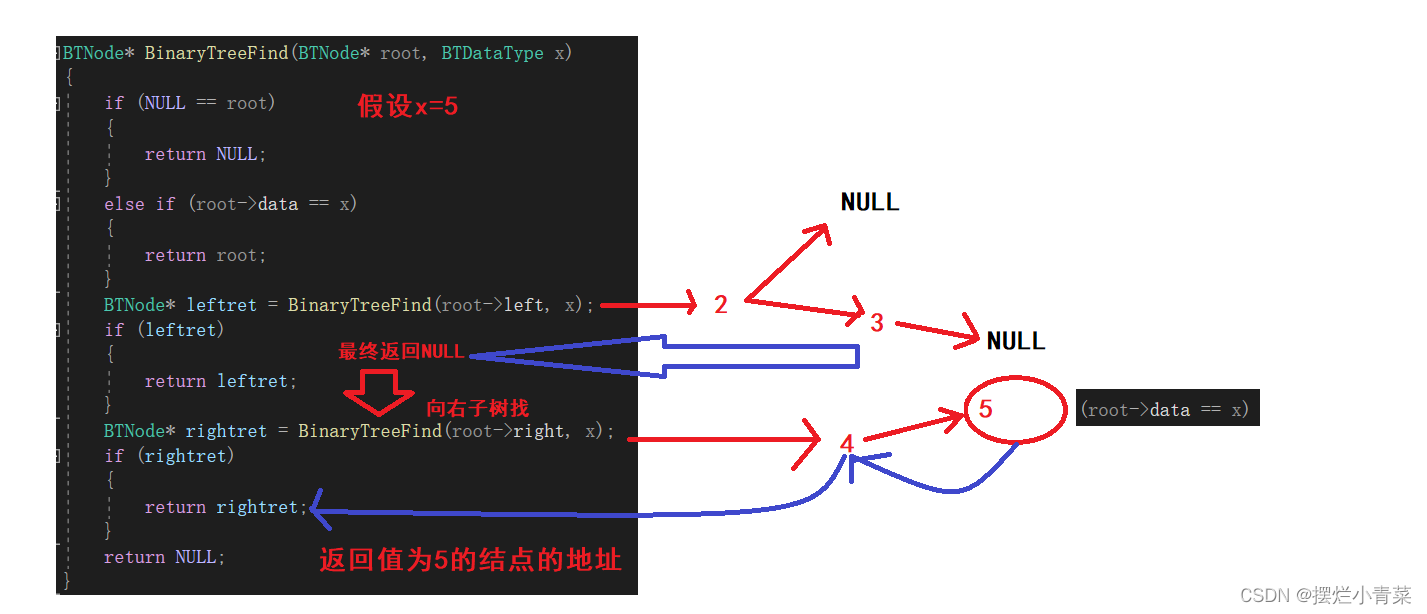
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {//寻找到空树则返回空(说明在某条连通路径上不存在待找结点)if (NULL == root){return NULL;}//判断树根是否为待找结点,若判断为真则返回该结点地址else if (root->data == x){return root;}//若树根不是要找的结点, 则往左子树找BTNode* leftret = BinaryTreeFind(root->left, x);if (leftret){return leftret;}//若左子树中不存在待找结点,则往右子树找BTNode* rightret = BinaryTreeFind(root->right, x);if (rightret){return rightret;}//若左右子树中都找不到则说明不存在待找结点,返回空return NULL; }将下图中的树的根结点地址传入递归函数:
递归函数执行过程的简单图示:
分治递归的思想是核心哦!!!!

相关文章:

数据结构:链式二叉树初阶
目录 一.链式二叉树的逻辑结构 1.链式二叉树的结点结构体定义 2.链式二叉树逻辑结构 二.链式二叉树的遍历算法 1.前序遍历 2.中序遍历 3.后序遍历 4.层序遍历(二叉树非递归遍历算法) 层序遍历概念: 层序遍历算法实现思路: 层序遍历代码实现: 三.链式二叉树遍历算…...

公式编写1000问9-12
9.问: 买入:日线创100日新高 ,周线(5周)BIAS>10 卖出:2日收盘在30线下方 注:买卖都只要单一信号即可,不要连续给出信号 我今天才开始学习编写,可是没有买入信号,不知道哪错了? B1…...

C++11:类的新功能和可变参数模板
文章目录1. 新增默认成员函数1.1 功能1.2 示例2. 类成员变量初始化3. 新关键字3.1 关键字default3.2 关键字delete补充3.3 关键字final和override4. 可变参数模板4.1 介绍4.2 定义方式4.3 展开参数包递归展开参数包优化初始化列表展开参数包逗号表达式展开参数包补充5. emplace…...
)
【Java学习笔记】15.Java 日期时间(1)
Java 日期时间 java.util 包提供了 Date 类来封装当前的日期和时间。 Date 类提供两个构造函数来实例化 Date 对象。 第一个构造函数使用当前日期和时间来初始化对象。 Date( )第二个构造函数接收一个参数,该参数是从 1970 年 1 月 1 日起的毫秒数。 Date(long …...
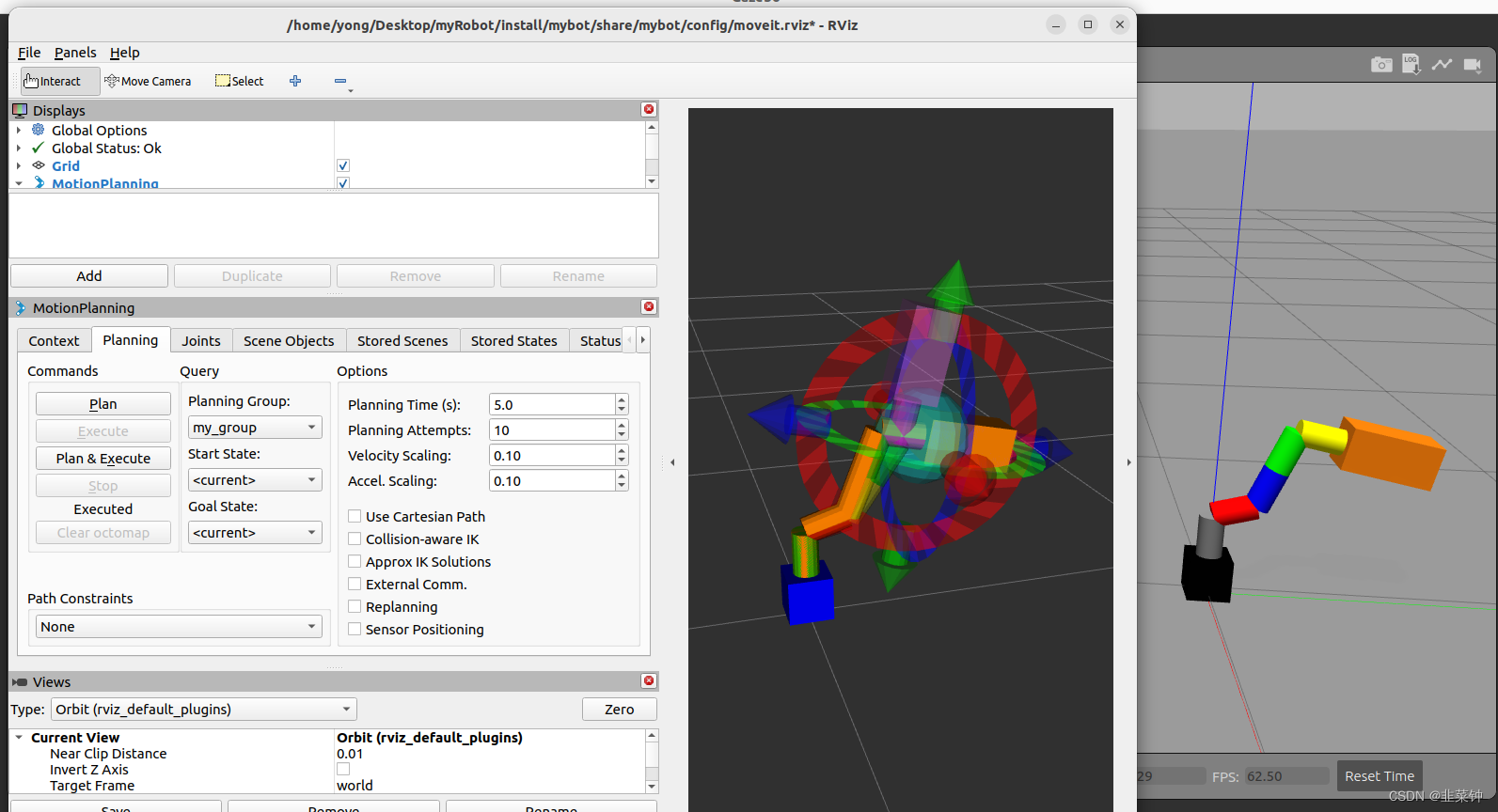
在ROS2中,通过MoveIt2控制Gazebo中的自定义机械手
目前的空余时间主要都在研究ROS2,最终目的是控制自己用舵机组装的机械手。 由于种种原因,先控制Gazebo的自定义机械手。 先看看目前的成果 左侧是rviz2中的moveit组件的机械手,右侧是gazebo中的机械手。在moveit中进行路径规划并执行后&#…...

Java-线程池 原子性 类
Java-线程池 原子性 类线程池构造方法调用Executors静态方法创建调用方法直接创建线程池对象原子性volatile-问题出现原因:volatile解决原子性AtomicInteger的常用方法悲观锁和乐观锁synchronized(悲)和CAS(乐)的区别并发工具类Hashtable集合ConcurrentHashMap原理:CountDownLa…...
力扣sql简单篇练习(二十五)
力扣sql简单篇练习(二十五) 1 无效的推文 1.1 题目内容 1.1.1 基本题目信息 1.1.2 示例输入输出 1.2 示例sql语句 # Write your MySQL query statement below SELECT tweet_id FROM Tweets WHERE CHAR_LENGTH(content)>151.3 运行截图 2 求关注者的数量 2.1 基本题目内…...
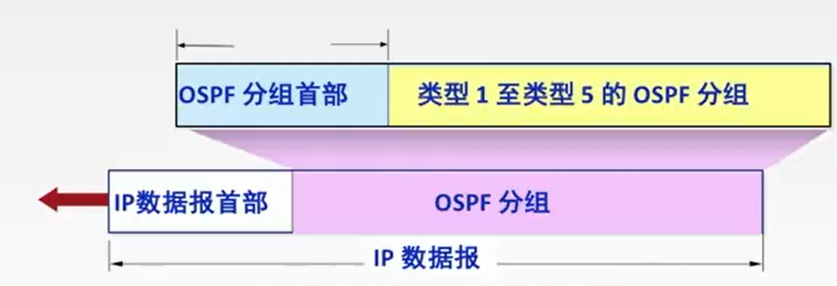
计算机网络:OSPF协议和链路状态算法
OSPF协议 开放最短路经优先OSPF协议是基于最短路径算法SPF,其主要特征就是使用分布式的链路状态协议OSPF协议的特点: 1.使用泛洪法向自治系统中的所有路由器发送信息,即路由器通过输出端口向所有相邻的路由器发送信息,而每一个相邻的路由器又…...

利用表驱动法+策略模式优化switch-case
1.前言 我有一个需求:有四个系统需要处理字段,一开始利用switch-case进行区分编码,后期字段处理越来越多,导致switch-case代码冗余,不太好,然后想通过java单继承多实现的性质进行优化。 2.实现 2.1定义S…...
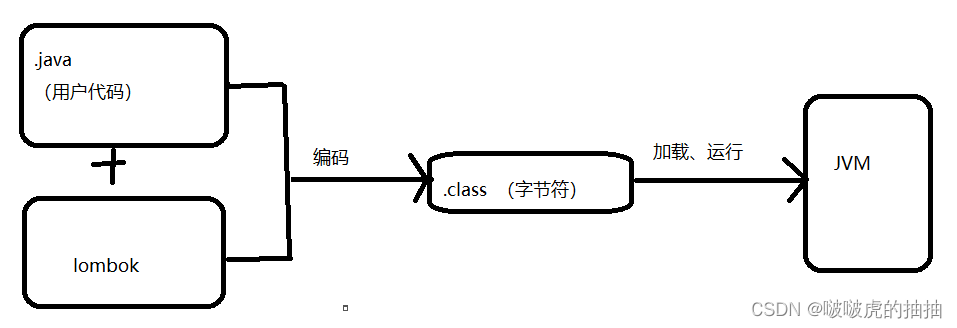
SpringBoot创建和使用
目录 什么是SpringBoot SpringBoot的优点 SpringBoot项目的创建 1、使用idea创建 2、项目目录介绍和运行 Spring Boot配置文件 1、配置文件 2、配置文件的格式 3、properties 3.1、properties基本语法 3.2、读取配置文件 3.3、缺点 4、yml 4.1、优点 4.2、yml基本…...

which、whereis、locate文件查找命令
Linux下查找文件的命令有which、whereis、locate和find,find命令因要遍历文件系统,导致速度较慢,而且还会影响系统性能,而且命令选项较多,就单独放一篇介绍,可参见find命令——根据路径和条件搜索指定文件_…...
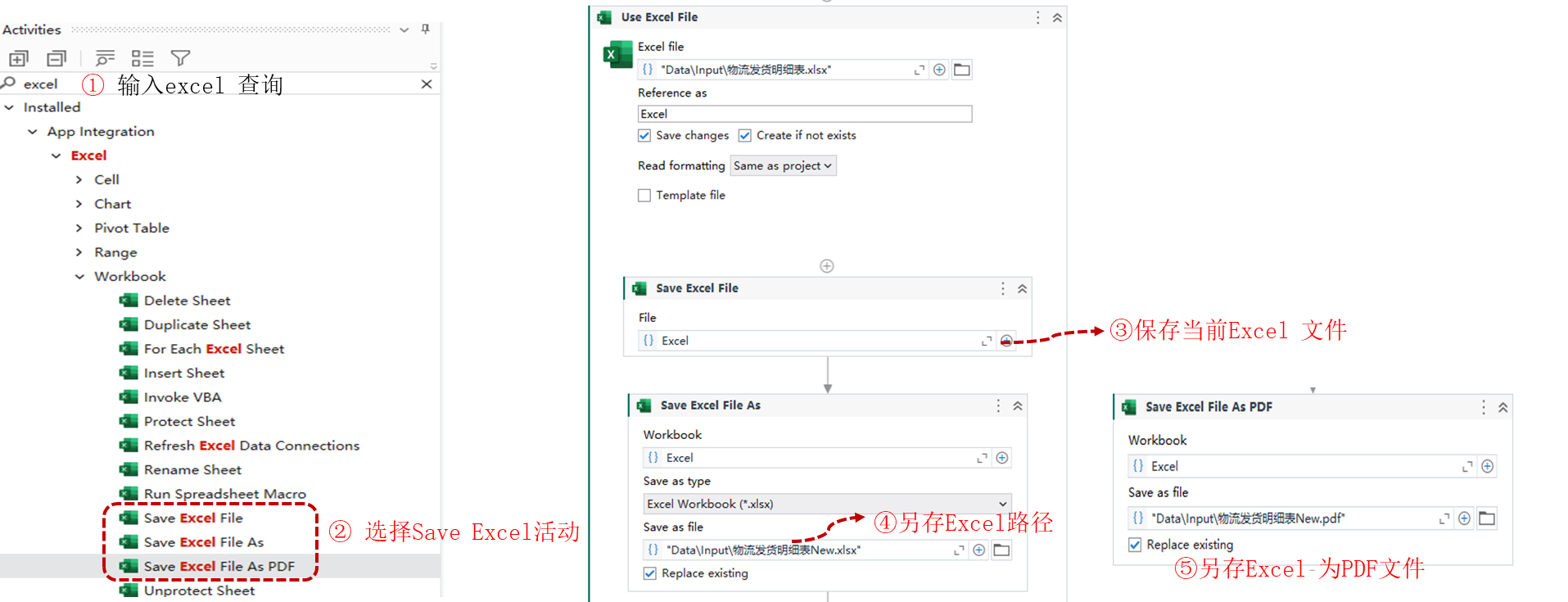
Uipath Excel 自动化系列14-SaveExcelFile(保存Excel)
活动描述 SaveExcelFile 保存Excel:保存工作簿,在修改 Excel 文件的用户界面自动化活动之后使用此活动,以保存对文件的更改 SaveExcelFile As 另存Excel : 将workbook 另存为文件 SaveExcelFile As PDF :将Excel 另存为PDF文件。该三个活…...
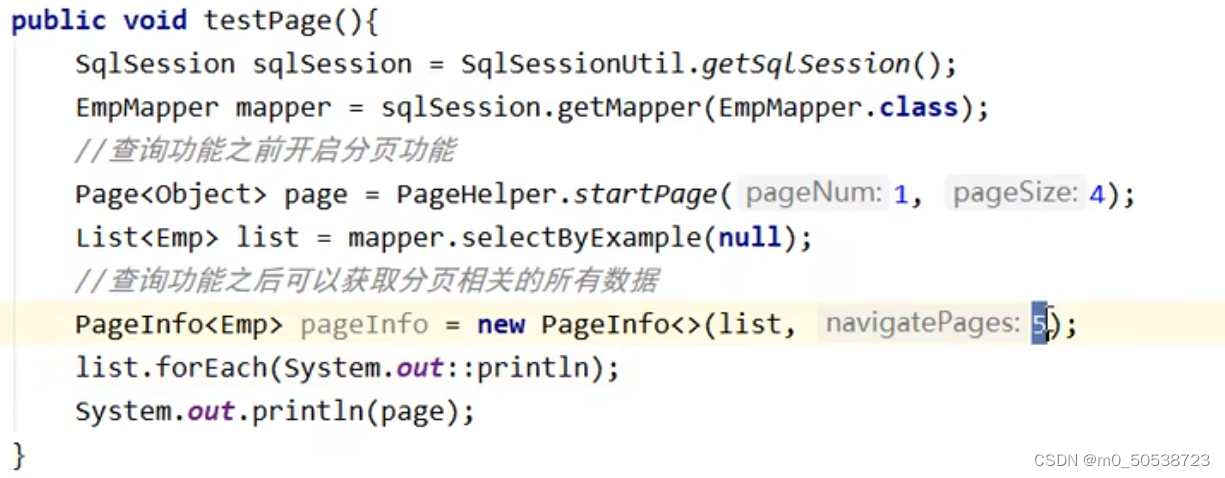
MyBatis学习
MyBatis优点 轻量级,性能出色 SQL 和 Java 编码分开,功能边界清晰。Java代码专注业务、SQL语句专注数据 开发效率稍逊于HIbernate,但是完全能够接受 补充:POJO 一:什么是POJO POJO的名称有多种,pure old…...
)
高速PCB设计指南系列(二)
第三篇 高速PCB设计 (一)、电子系统设计所面临的挑战 随着系统设计复杂性和集成度的大规模提高,电子系统设计师们正在从事100MHZ以上的电路设计,总线的工作频率也已经达到或者超过50MHZ,有的甚至超过100MHZ。目前…...

uniapp项目打包上线流程
平台:h5小程序app (安卓)小程序打包上线流程第一步:登录小程序公众平台第二步:hbuilderx打包小程序1.在mainfest.json文件中进行相关配置2.需要将项目中的网络请求改为https协议做为生产环境(配置项目的环境…...
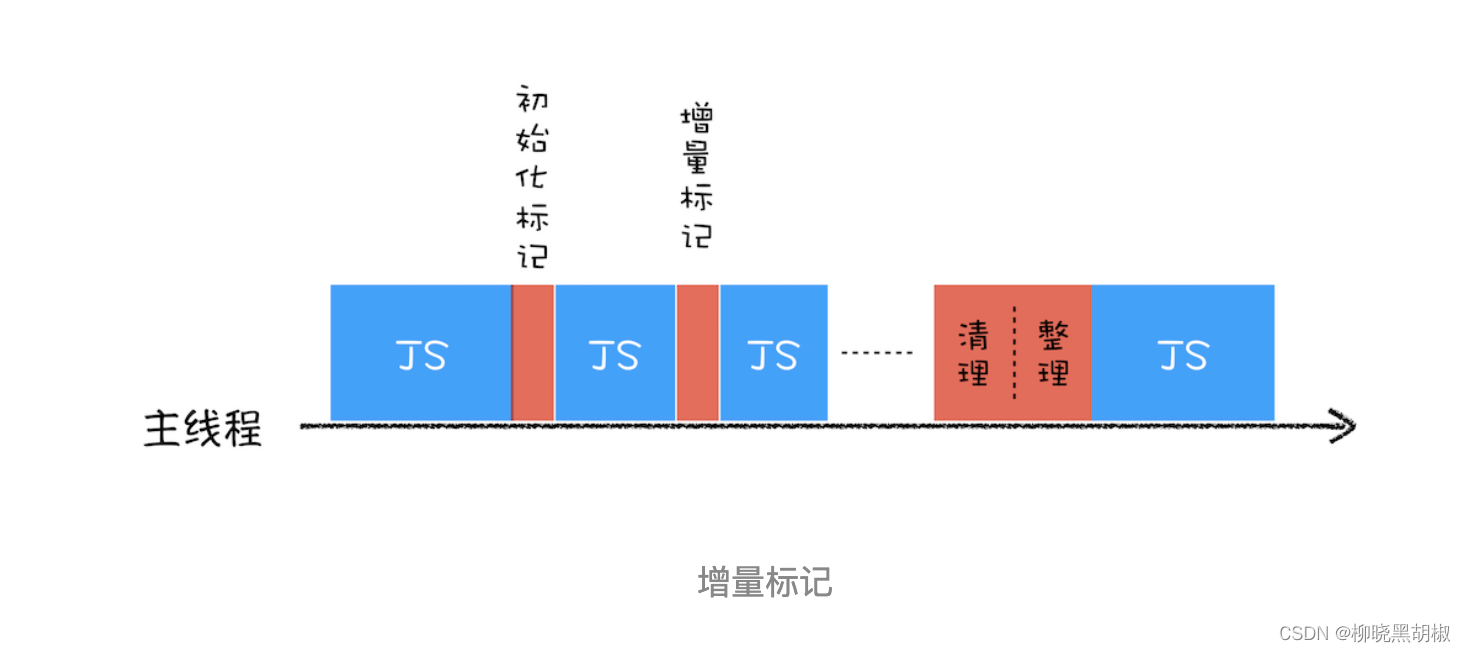
垃圾回收:垃圾数据如何自动回收
有些数据被使用之后,可能就不再需要了,我们把这种数据称为垃圾数据。如果这些垃圾数据一直保存在内存中,那么内存会越用越多,所以我们需要对这些垃圾数据进行回收,以释放有限的内存空间 不同语言的垃圾回收策略 通常…...

苹果笔不用原装可以吗?Apple Pencil平替笔推荐
近些年来,不管是学习还是画画,都有不少人喜欢用ipad。而ipad的用户,也是比较重视它的实用价值,尤其是不少人都想要好好利用来进行学习记笔记。事实上,有很多替代品都能替代Apple Pencil,仅仅用于记笔记就没…...
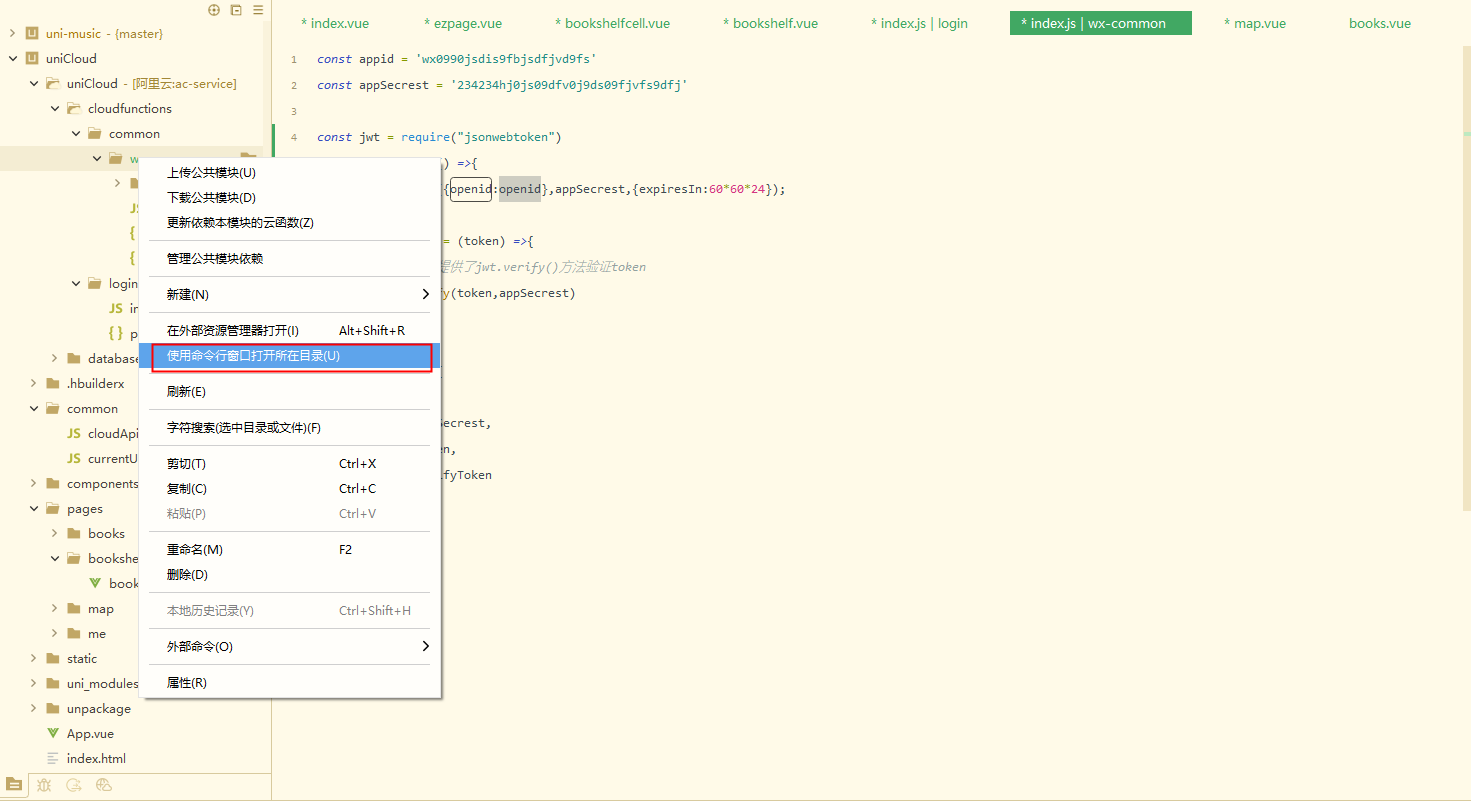
uniCloud基础使用-杂文
获取openID云函数use strict; exports.main async (event, context) > {//event为客户端上传的参数console.log(event : , event)// jscode2session 微信小程序登录接口,获取openidconst {code} event;// 云函数中如需要请求其他http服务,则使用uni…...
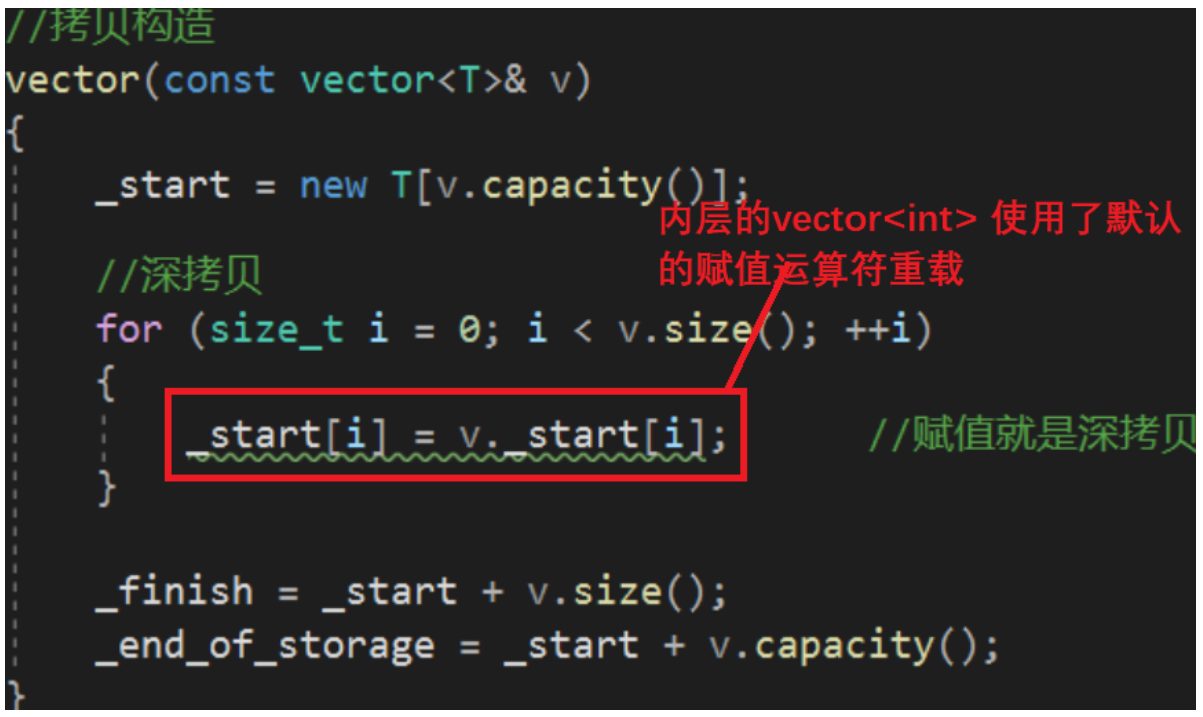
vector的模拟实现
文章目录vector的模拟实现vector 结构定义1. vector的迭代器的实现2. vector四个默认成员函数2.1 构造函数2.1.1 无参2.1.2 n个val初始化2.1.3 迭代器初始化2.2 析构函数2.3 拷贝构造函数2.3.1 传统写法2.3.2 现代写法2.4 赋值重载运算符3. 管理数组相关接口3.1 reserve3.2 res…...
【无标题】compose系列教程-4.相对布局ConstraintLayout的使用
相对布局在Compose中被称为ConstraintLayout,它可以让您以相对于其他元素的方式放置元素。 以下是使用ConstraintLayout实现相对布局的示例代码: Composable fun ConstraintLayoutExample() { ConstraintLayout(modifier Modifier.fillMaxSize()…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...