「动态规划」当小偷改行去当按摩师,会发生什么?
一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),返回总的分钟数。
- 输入:[1,2,3,1],输出:4,解释:选择1号预约和3号预约,总时长 = 1 + 3 = 4。
- 输入:[2,7,9,3,1],输出:12,解释:选择1号预约、3号预约和5号预约,总时长 = 2 + 9 + 1 = 12。
- 输入:[2,1,4,5,3,1,1,3],输出:12,解释:选择1号预约、3号预约、5号预约和8号预约,总时长 = 2 + 4 + 3 + 3 = 12。
这题是打家劫舍问题的变形。你个小偷换了个马甲,我就不认识你了?我们用动态规划的思想来解决这个问题。
确定状态表示:根据经验和题目要求,我们用dp[i]表示,选择完i位置之后,此时的最长预约时长。再细分为:
- 用f[i]表示,接受i位置的预约之后,此时的最长预约时长。
- 用g[i]表示,不接受i位置的预约之后,此时的最长预约时长。
推导状态转移方程:
- 如果接受i位置的预约,那么就不能接受i - 1位置的预约。所以,接受i位置的预约之后的最长预约时长,就等于不接受i - 1位置的预约之后的最长预约时长加上i位置的预约的时长,即f[i] = g[i - 1] + nums[i]。
- 如果不接受i位置的预约,那么既可以接受i - 1位置的预约,也可以不接受i - 1位置的预约。由于没有接受i位置的预约,所以此时的最长预约时长和选择完i - 1位置之后的最长预约时长相同,要么是接受i - 1位置的预约之后的最长预约时长f[i - 1],要么是不接受i - 1位置的预约之后的最长预约时长g[i - 1]。所以不接受i位置的预约的最长预约时长是这两者的较大值,即g[i] = max(f[i - 1], g[i - 1])。
综上所述:f[i] = g[i - 1] + nums[i],g[i] = max(f[i - 1], g[i - 1])。
初始化:根据状态转移方程,由于f[i]和g[i]都依赖于i - 1位置的值,所以我们要初始化f[0]和g[0]。
- f[0]表示接受0位置的预约之后,此时的最长预约时长,显然就是0位置的预约时长,即f[0] = nums[0]。
- g[0]表示不接受0位置的预约之后,此时的最长预约时长,显然g[0] = 0。
综上所述:f[0] = nums[0],g[0] = 0。
填表顺序:根据状态转移方程,f[i]依赖于g[i - 1],g[i]依赖于f[i - 1]和g[i - 1],所以应从左往右填表,且同时填f表和g表。
返回值:假设有n个预约。题目要求我们返回,在选择完n - 1位置的预约之后,最长的预约时长。由于并不确定是否接受n - 1位置的预约,再根据状态表示,我们应返回f[n - 1]和g[n - 1]的较大值。
细节问题:f表和g表的规模和nums的规模相同,都是1 x n。另外,如果nums为空,直接返回0即可。
时间复杂度:O(N),空间复杂度:O(N)。
class Solution {
public:int massage(vector<int>& nums) {int n = nums.size();// 处理边界情况if (n == 0) {return 0;}// 创建dp表vector<int> f(n);auto g = f;// 初始化f[0] = nums[0];// 填表for (int i = 1; i < n; i++) {for (int j = 1; j < n; j++) {f[i] = g[i - 1] + nums[i];g[i] = max(f[i - 1], g[i - 1]);}}return max(f[n - 1], g[n - 1]);}
};相关文章:

「动态规划」当小偷改行去当按摩师,会发生什么?
一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),…...

Python | 排队取奶茶
队列的基本概念(队头、队尾)和特点(先入先出) 在 Python 语言中,标准库中的queue模块提供了多种队列的实现,比如普通队列和优先级队列,因此你可以使用queue.Queue类来创建队列,不过…...
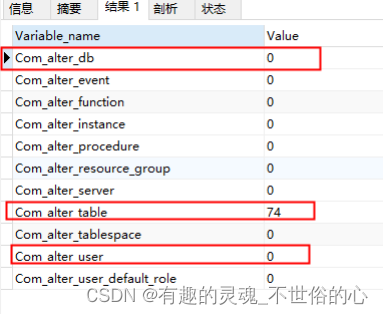
mysql当前状态分析(show status)
文章目录 查看当前线程数据查询连接情况查询缓存相关查询锁相关查询增删改查执行次数查询DDL创建相关 SHOW STATUS 是一个在 MySQL 中用来查看服务器运行状态的命令。它可以帮助你了解服务器的当前性能,包括连接数、表锁定、缓冲区使用情况等信息。 查看当前线程数据…...
——使用机器学习进行金三角大米分布图)
Google Earth Engine(GEE)——使用机器学习进行金三角大米分布图
第 1 步:转到https://code.earthengine.google.com/打开代码编辑器 第 2 步:使用以下代码从 Google Earth Engine Asset 导入数据 // 导入影像集合 var composites = ee.ImageCollection("projects/servir-mekong/yearlyComposites"); // 导入训练数据 var data …...

MyBatis一级和二级缓存介绍
MyBatis是一个持久层框架,它提供了一级缓存和二级缓存来提高数据库操作的性能。下面是一级缓存和二级缓存的区别理解、画图和知识点总结: 一级缓存: 一级缓存是MyBatis默认开启的缓存层,它是SqlSession级别的缓存,也…...

PowerDesigner遍历导出所有表结构到Excel
PowerDesigner遍历导出所有表到Excel 1.打开需要导出表结构到Excel的pdm文件 2.点击Tools|Execute Commands|Edit/Run Script菜单或按下快捷键Ctrl Shift X打开脚本窗口,输入示例VBScript脚本,修改其中的Excel模板路径及工作薄页签,点Run…...
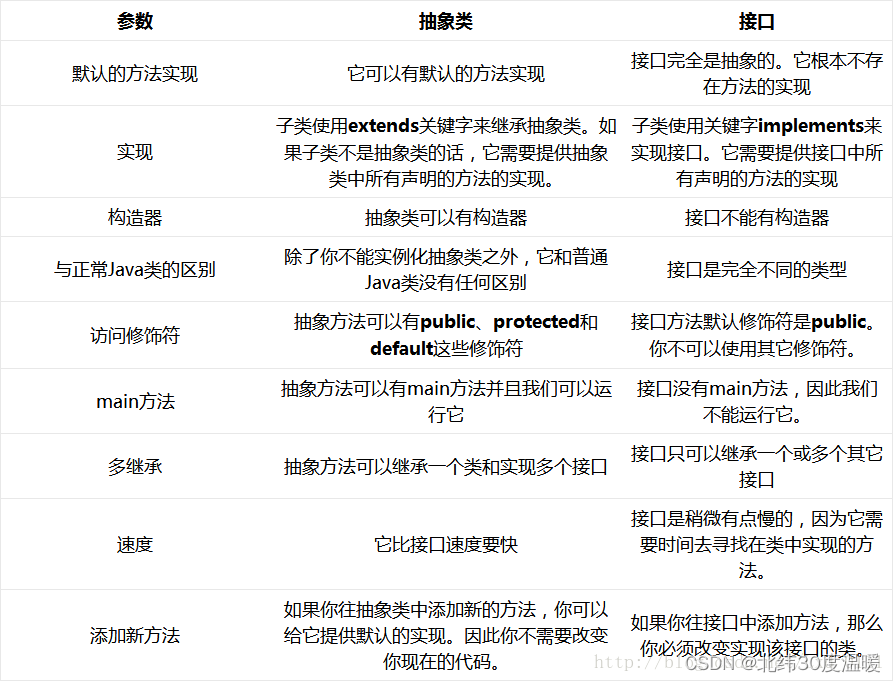
JavaSE——抽象类和接口
目录 一 .抽象类 1.抽象类概念 2.抽象类语法 3.抽象类特性 4.抽象类的作用 二. 接口 1.接口的概念 2.语法规则 3.接口的使用 4.接口特性 5.实现多个接口 6.接口间的继承 三.抽象类和接口的区别 一 .抽象类 1.抽象类概念 在面向对象的概念中,所有的对…...
生成式人工智能 - stable diffusion web-ui安装教程
一、Stable Diffusion WEB UI 屌丝劲发作了,所以本地调试了Stable Diffusion之后,就去看了一下Stable Diffusion WEB UI,网络上各种打包套件什么的好像很火。国内的也就这个层次了,老外搞创新,国内跟着屁股后面搞搞应用层,就叫大神了。 不扯闲篇了,我们这里从git源码直接…...
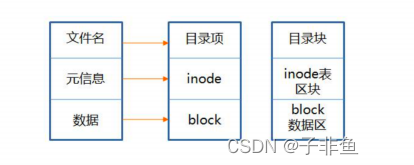
11-Linux文件系统与日志分析
11.1深入理解Linux文件系统 在处理Liunx系统出现故障时,故障的症状是最易发现。数学LInux系统中常见的日志文件,可以帮助管理员快速定位故障点,并及时解决各种系统问题。 11.1.1 inode与block详解 文件系统通常会将这两部分内容分别存放在…...
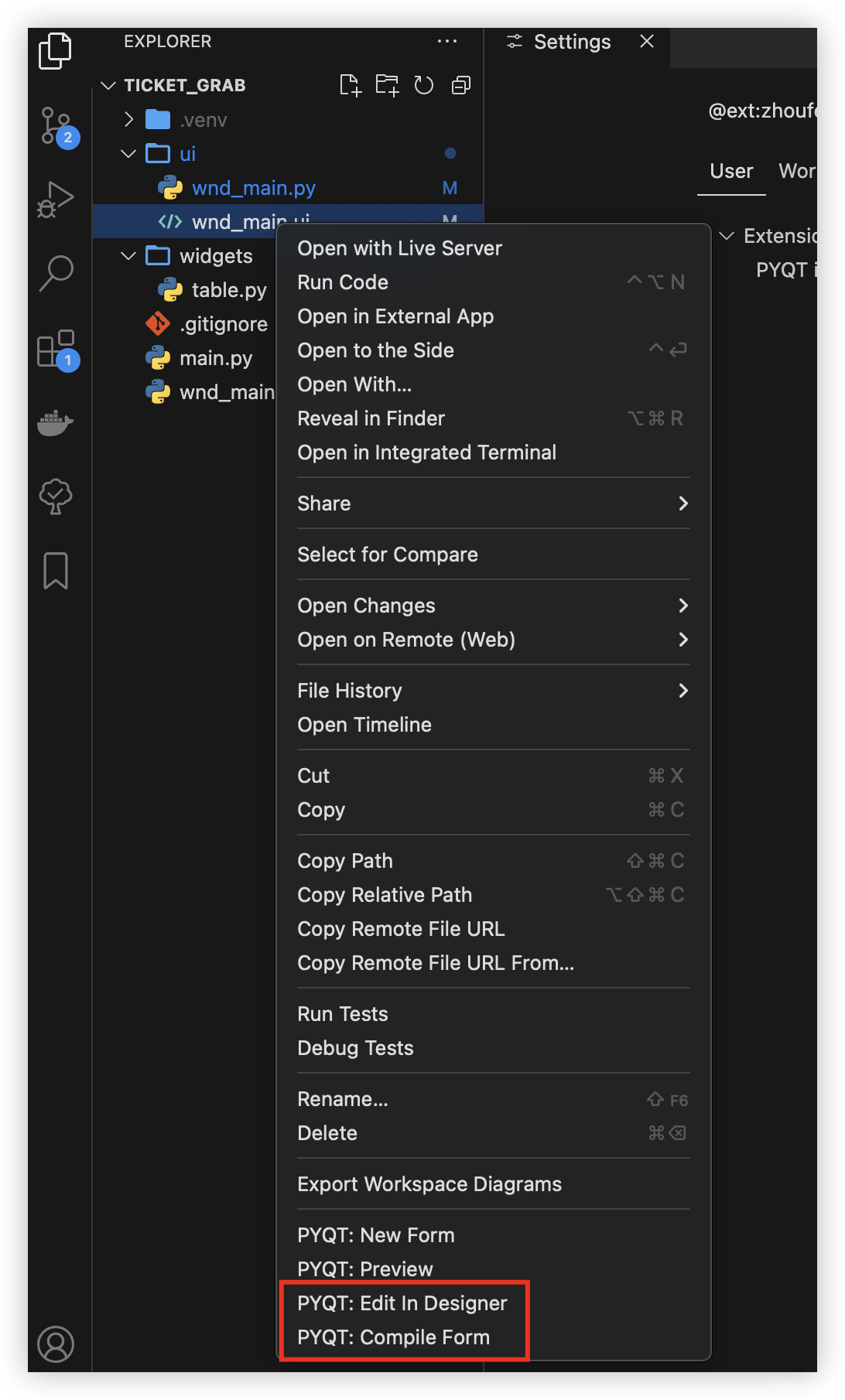
mac M1下安装PySide2
在M1下装不了PySide2, 是因为PySide2没有arm架构的包 1 先在M1上装qt5 安装qt主要是为了能用里面的Desinger, uic, rcc brew install qt5 我装完的路径在/opt/homebrew/opt/qt5 其中Designer就是用来设计界面的 rcc用resource compiler, 编绎rc资源文件的, 生成对应的py文件…...

超详解——识别None——小白篇
目录 1. 内建类型的布尔值 2. 对象身份的比较 3. 对象类型比较 4. 类型工厂函数 5. Python不支持的类型 总结: 1. 内建类型的布尔值 在Python中,布尔值的计算遵循如下规则: None、False、空序列(如空列表 [],空…...

C++的MQTT开发:使用Paho的C++接口实现消息发布、订阅、连接RabbitMQ
C Paho实现MQTT消息发布功能 要使用paho的cpp接口实现发布MQTT消息的功能,需要进行以下步骤: 安装paho库:首先从paho官方网站下载并安装paho的C库。可以从https://www.eclipse.org/paho/clients/cpp/ 下载适合操作系统的版本。 创建MQTT客户…...

深度网络学习笔记(二)——Transformer架构详解(包括多头自注意力机制)
Transformer架构详解 前言Transformer的整体架构多头注意力机制(Multi-Head Attention)具体步骤1. 步骤12. 步骤23. 步骤34. 步骤4 Self-Attention应用与比较Self-Attention用于图像处理Self-Attention vs. CNNSelf-Attention vs. RNN Transformer架构详…...
Python 快速查找并替换Excel中的数据
Excel中的查找替换是一个非常实用的功能,能够帮助用户快速完成大量数据的整理和处理工作,避免手动逐一修改数据的麻烦,提高工作效率。要使用Python实现这一功能, 我们可以借助Spire.XLS for Python 库,具体操作如下&am…...

KafkaStream Local Store和Global Store区别和用法
前言 使用kafkaStream进行流式计算时,如果需要对数据进行状态处理,那么常用的会遇到kafkaStream的store,而store也有Local Store以及Global Store,当然也可以使用其他方案的来进行状态保存,文本主要理清楚kafkaStream…...
PowerDesigner导入Excel模板生成数据表
PowerDesigner导入Excel模板生成数据表 1.准备好需要导入的Excel表结构数据,模板内容如下图所示 2.打开PowerDesigner,新建一个physical data model文件,填入文件名称,选择数据库类型 3.点击Tools|Execute Commands|Edit/Run Script菜单或按下快捷键Ctrl Shift X打开脚本窗口…...

STM32 HAL库开发——入门篇(3):OLED、LCD
源自正点原子视频教程: 【正点原子】手把手教你学STM32 HAL库开发全集【真人出镜】STM32入门教学视频教程 单片机 嵌入式_哔哩哔哩_bilibili 一、OLED 二、内存保护(MPU)实验 2.1 内存保护单元 三、LCD 3.1 显示屏分类 3.2 LCD简介 3.3 LCD…...

在Linux中查找文件命令的几种方法
要在Linux中查找文件,可以使用以下几种不同的实现方法: 1. 使用find命令: find <搜索路径> <搜索选项> <搜索条件><搜索路径>:表示要搜索的起始路径,可以是一个具体的目录路径,也…...

【TB作品】MSP430F5529 单片机,温度控制系统,DS18B20,使用MSP430实现的智能温度控制系统
作品功能 这个智能温度控制系统基于MSP430单片机设计,能够实时监测环境温度并根据预设的温度报警值自动调节风扇和加热片的工作状态。主要功能包括: 实时显示当前温度。通过OLED屏幕显示温度报警值。通过按键设置温度报警值。实际温度超过报警值时&…...

立创小tips
立创小tips 原理图中 1-修改图纸属性 保存完,绘制原理图的界面就出现了,然后我们鼠标点击原理图的边缘变成红色就可以高边表格的属性了。 2-鼠标右键可以移动整个原理图 3-查看封装 点击任意一个元器件,在右侧就会显示封装属性ÿ…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
