【排序算法】快速排序
一、定义:
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法(也叫Hoare排序),是一种基于分治的排序方。其基本原理是将待排序的数组通过一趟排序分成两个独立的部分,其中一部分的所有数据比另一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列(非递归也是可行的,需要借助数据结构栈来实现)
二、递归思想:
排序只讲升序,升序和降序也就是大于和小于逻辑上的差别
Hoare法:
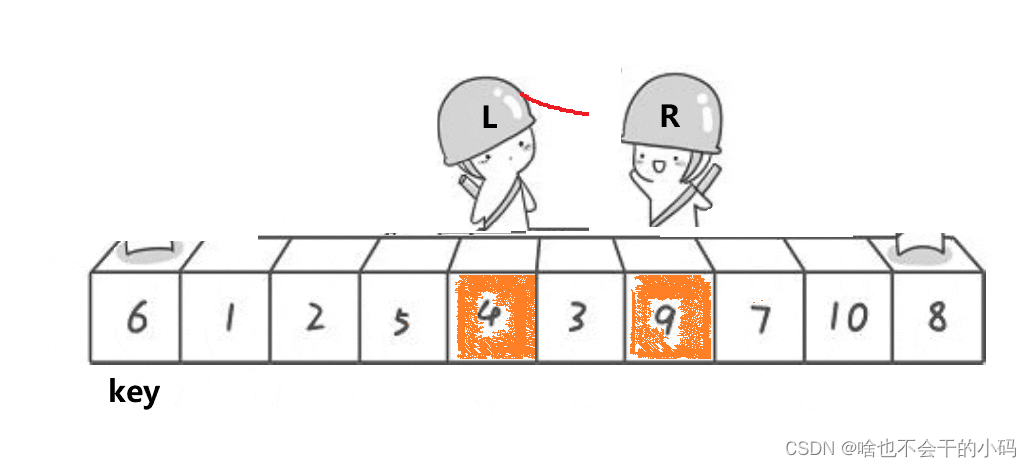
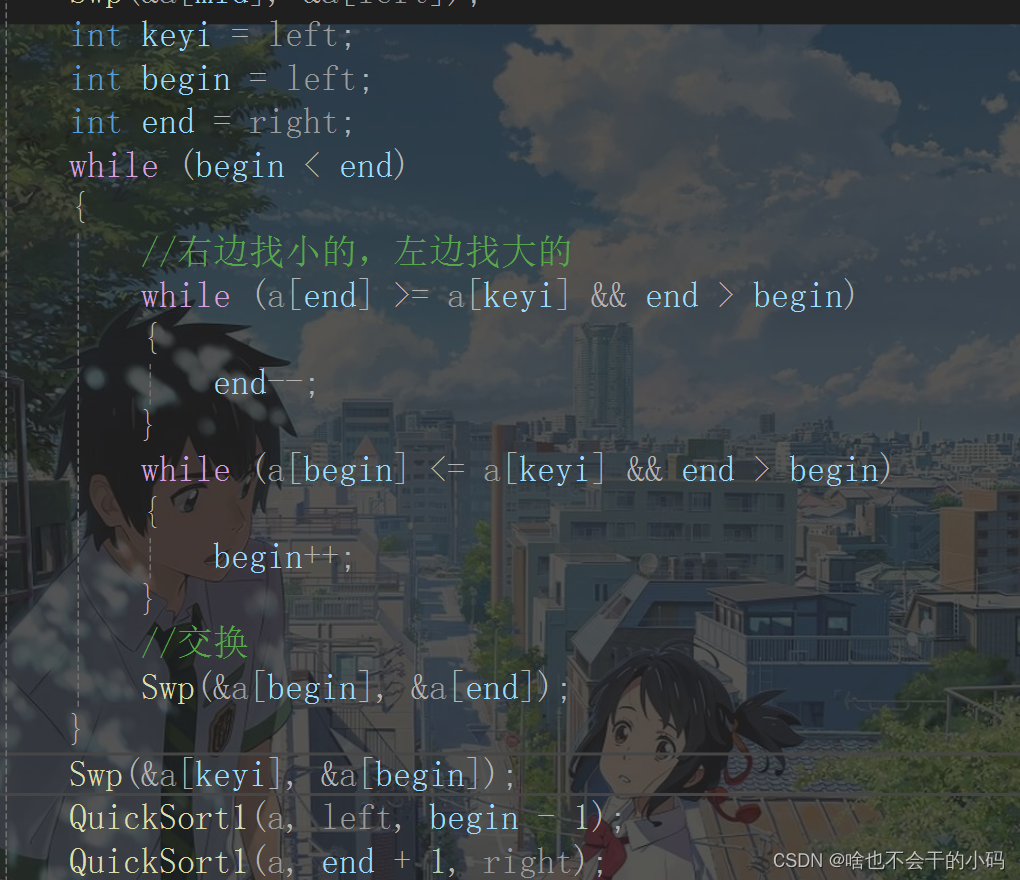
1、设置一个keyi记录头位置的数据,然后设计2个指分别为针end和begin; 一个从右边出发,一个从左边出发
2、end所指向的数据若是小于keyi则停下,然后begin走,所指向的数据若是大于keyi则停下,
3、将end和begin指向的元素进行互换
4、继续让end走,然后begin走,重复2-3,直到2者相遇,若是相遇,则将其与keyi指向的元素进交换,完成一次✨👉👉
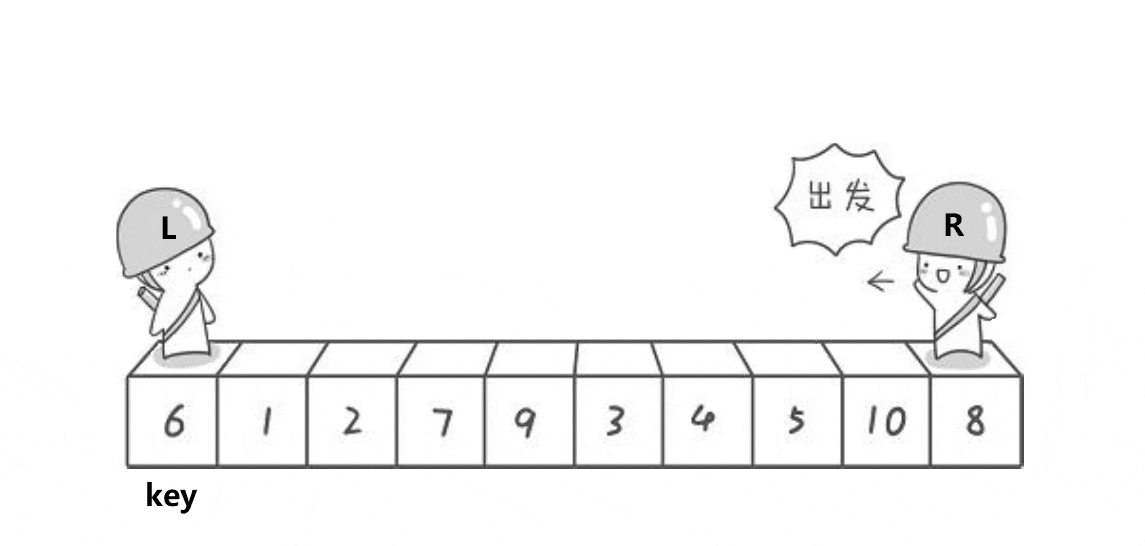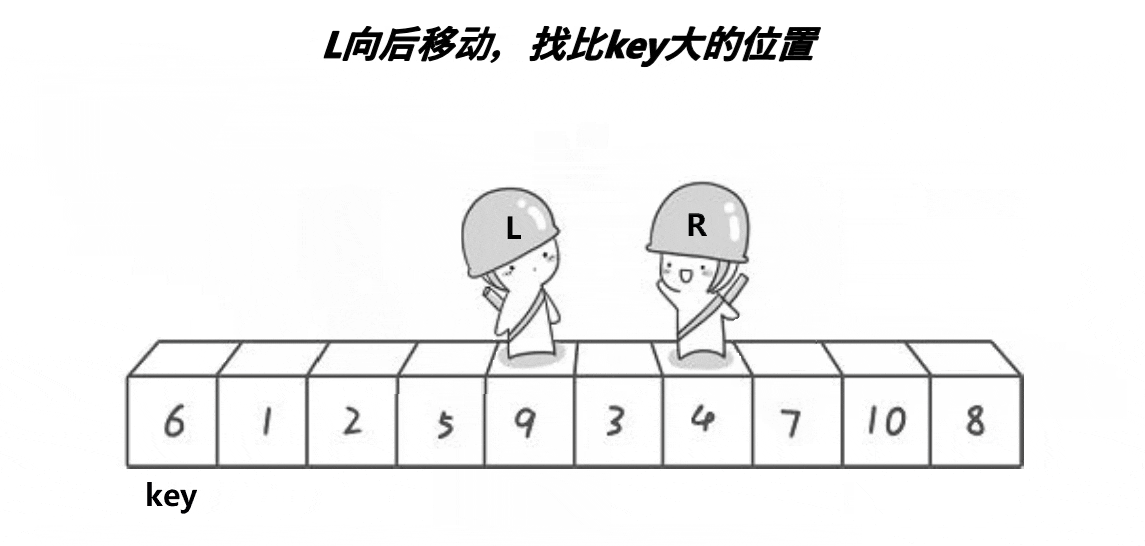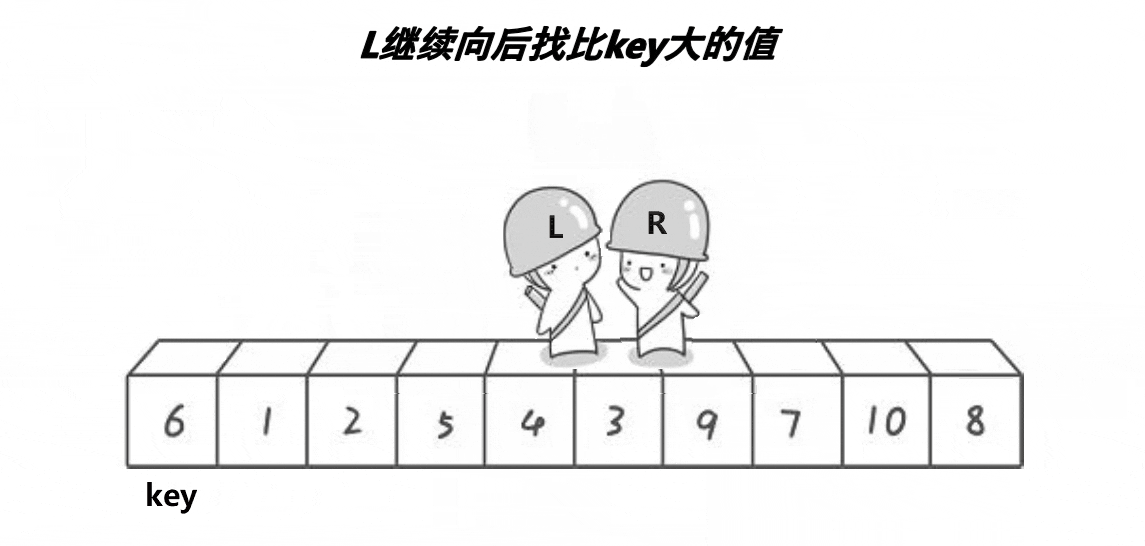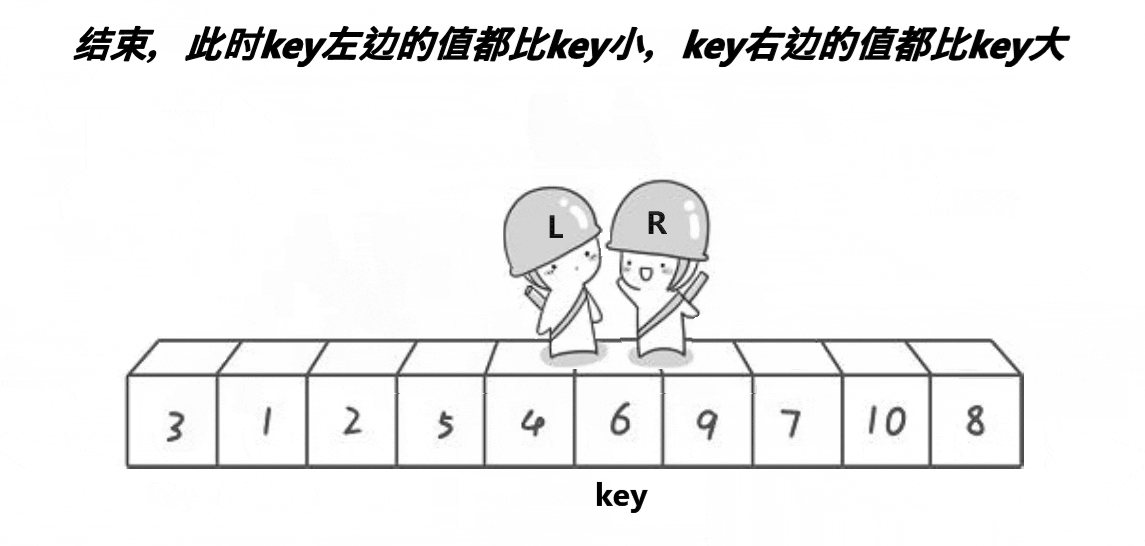
5、keyi指向的数据的位置不是交换到了end和begin相遇的地方么,我们从这里以此处为界限,将区间分成2部分👉👉👉
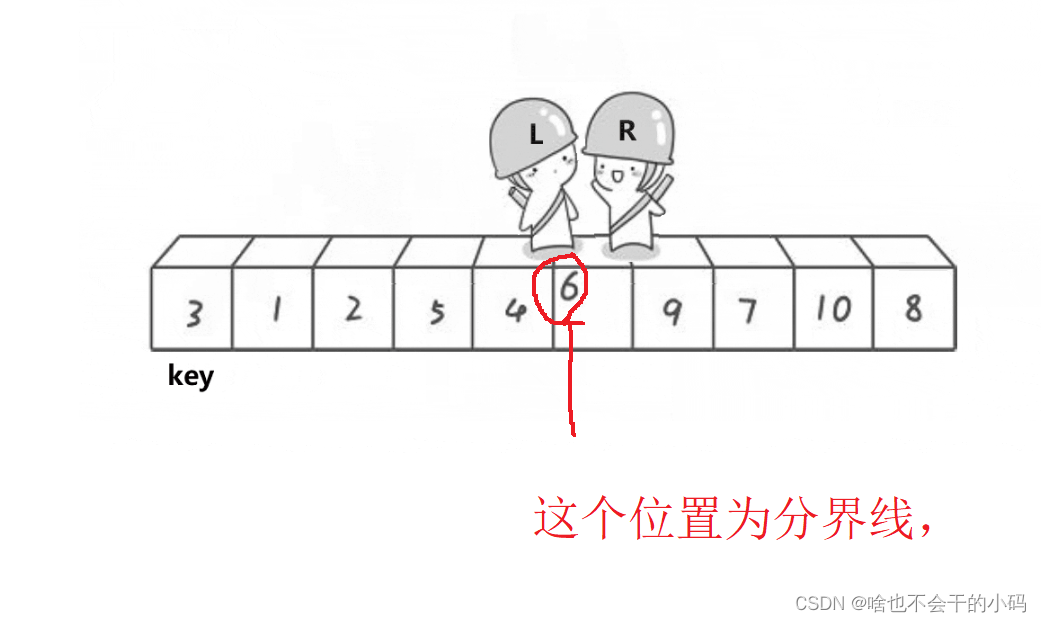
也就是说我们要对左和右区间分别进行上述操作(2个人走路对比交换操作),完成2个区间,2个区间又会分化成4个区间,一直进行下去,分到区间只有一个数据就实现了。🤔🤔🤔有点类似与二叉树里的前序遍历的思想✨✨✨
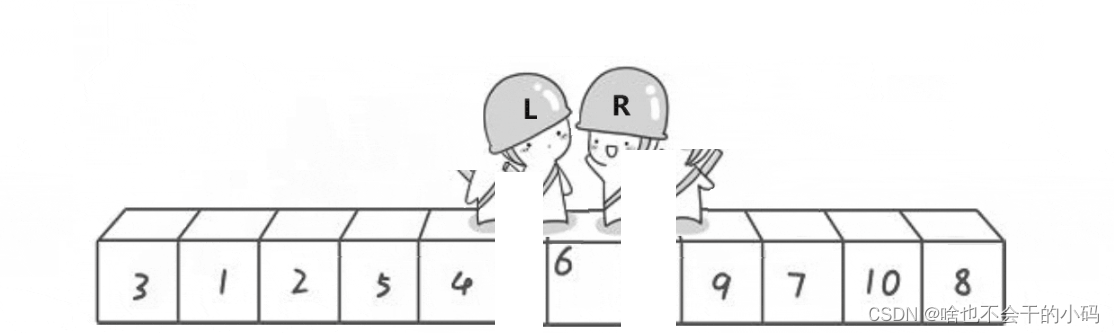
我们发现走完一次中间值的特点是左边全部小于他,右边全部大于他
我们走路的先后是有讲究的,2个人不是同时走的,而是一个人先走,一个人慢走,也就是说满足这个特点的话讲究先后顺序,因为决定了谁先遇见谁 那么如果我要左边先走了????🤔
✨✨✨用图来说话,是不是不能满足了;
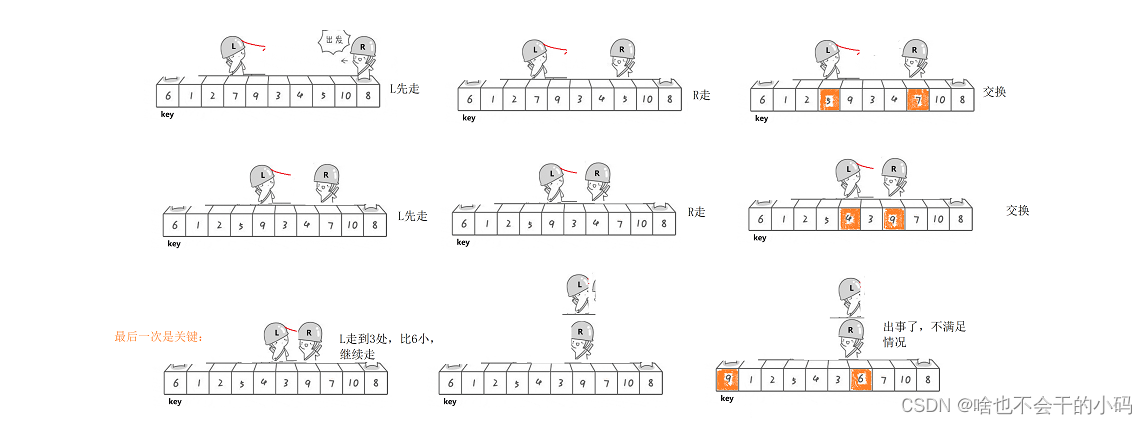
🐸🐸hoare排序的难点在这里,就是要注意谁先走;为啥会有这种情况??
✨✨因为我们左边的任务是找大,右边的任务是找小,然后而且我们的2个好兄弟并不是同时走的,是交替顺序走的哦!🧑🎓🧑🎓相遇前的最后一次发生的交换,如下:这是互换好的
此时🐸左边大于keyi的数换到了end的位置,🐸右边小于keyi的数换到了begin的位置。🤔如果先走begin;begin走到end的位置停下,也就是我们会将大于keyi的数和其交换位置,所以不满足情况;若是先走end,那么end和begin相遇就是停在小于keyi的位置✨✨
其实这个才是影响最终结果的情况
👉✨总结:“先出发是为了在你遇见我之前而遇见你”---->>>我如果keyi的位置在首元素位置,和keyi进行互换的元素需要是小于keyi指向的元素,那么就需要任务为:找大于keyi的数的end指针先走;如果keyi在尾元素处,最后与keyi交换的元素要大于keyi指向的元素,那么我们需要的是任务为:找大于keyi的begin指针先走。✨✨✨✨✨✨✨✨✨✨✨✨✨
Hoare的思路差不多讲完了,是不是感觉已经可以自己写出代码了✨✨✨✨确实如此哈,但是你这会递归吗??🧐 哈哈哈,开玩笑啦❤️🫰笔者当然相信你会的,试着自己写一下嘛😁作为笔记,我还是记录一下
🧑🎓✨开始时就说过Hoare排序类似二叉树的前序,先排序,当keyi换好位置后,将其当作“根节点”并分成2个区间,2个区间又进行排序,将keyi位置交换好,再次以keyi根分成2个区间,重复排序,一直分到区间只有一个元素,也就有序了,👉👉👉这个图就是先分区间,排序好后,分成2部分,因为每次排一次keyi交换后,他的左边全是小于他的值 右边全是大于他的值,每个区间的都有这样的特性,因此传参传的是区间✨
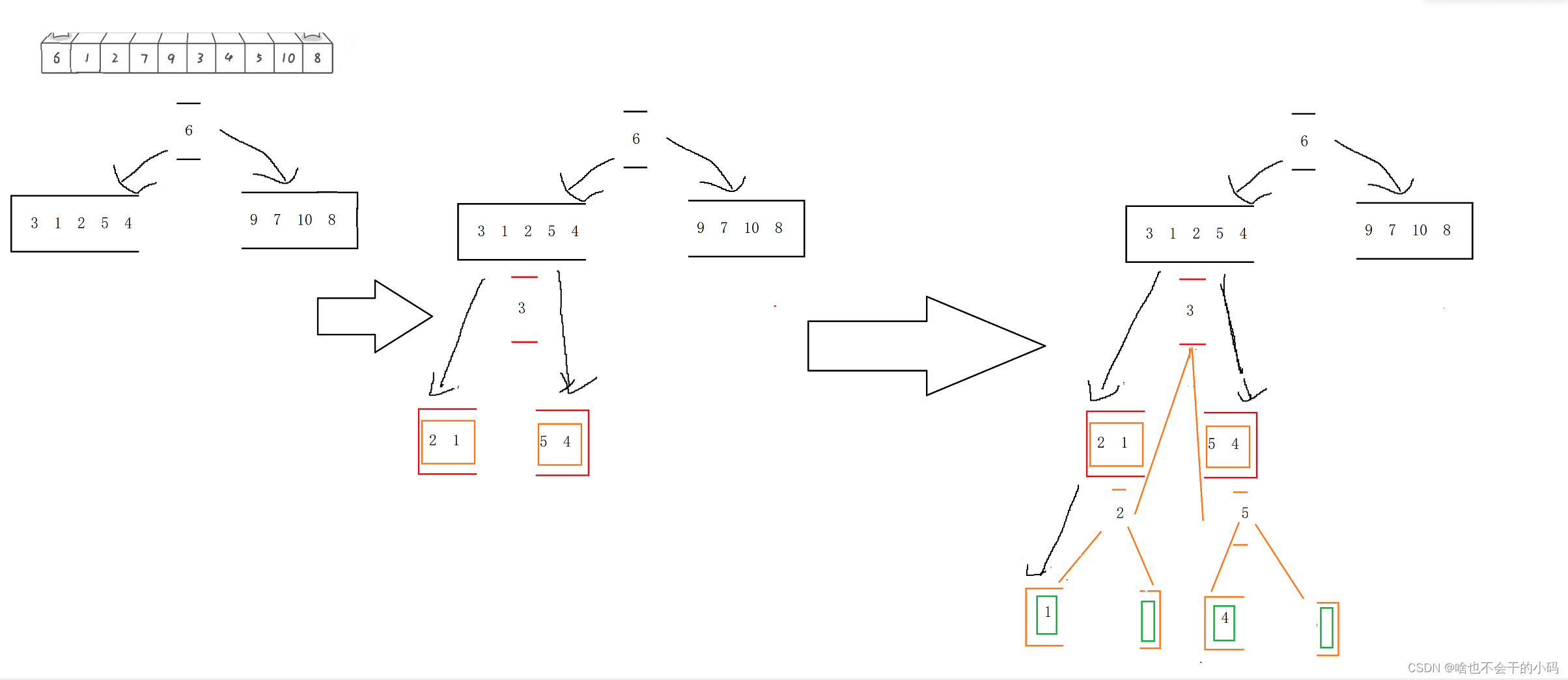
我们排号区间,以节点作为区间分界点进行分割区间,如6的左右2边分成了2块区间
优化1:keyi的选取
✨✨其实上面的递归看着是个二叉树的样子,keyi每次都换在区间中间的情况,并不是每次都是这样,根据待排序数组来看的哦🐸 数据顺序千变万化;
👉比如:一个逆序的数组,你将数据传入,那么keyi直接交换到最后一个位置,以最后一个位置分成一个区间;看图,发现了么,我还有重复排序情况,很容易发生栈溢出的风险☠️☠️
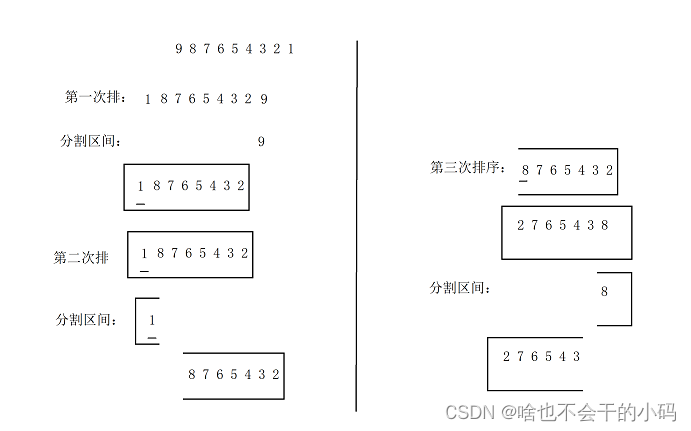
如果是 顺序的也是如此👉👉👉👉
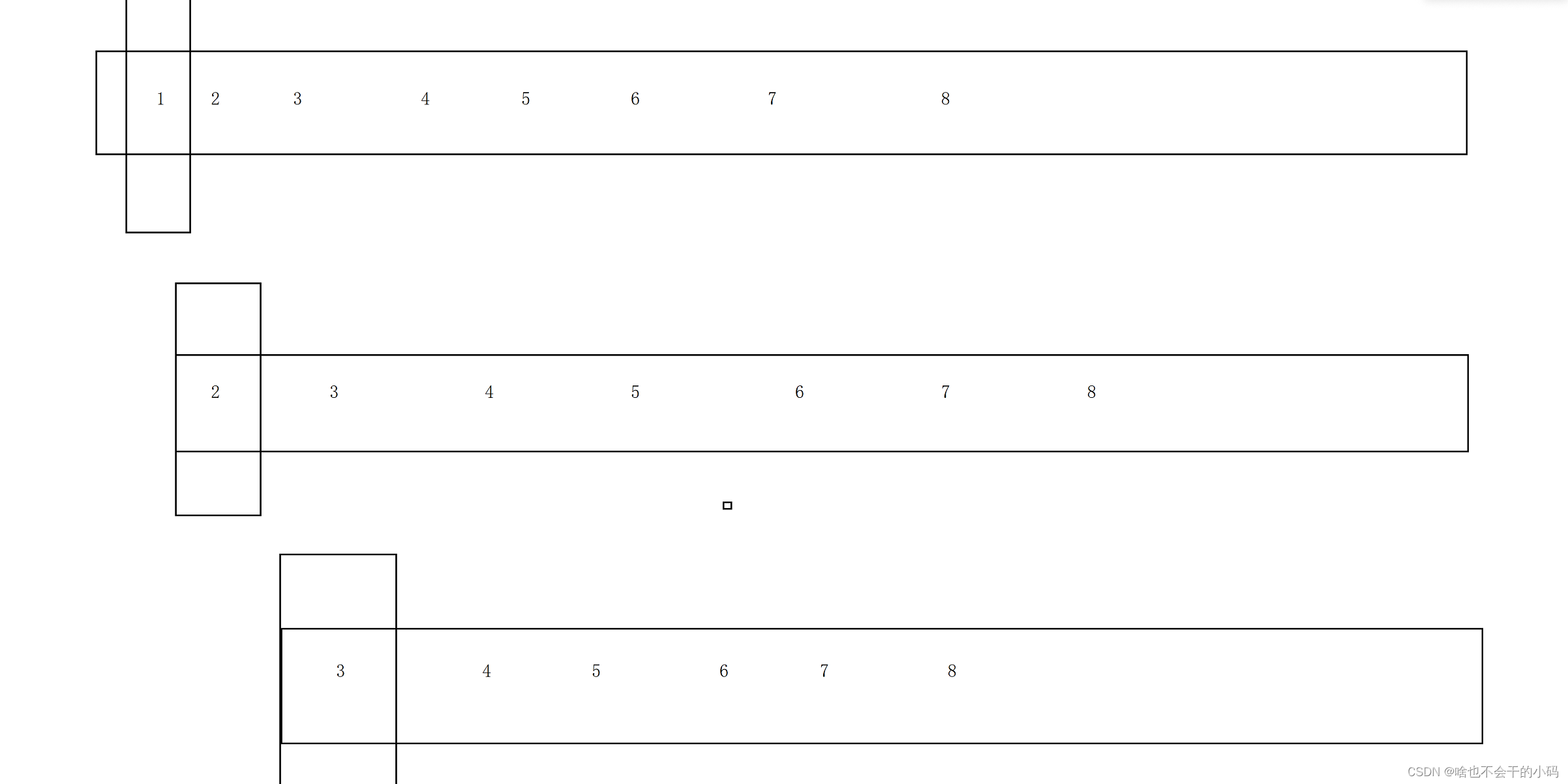
时间复杂度退化到O(N^2)🤔🤔
因为keyi每次都是取首元素的值,所以会出现上述这种弊端,从keyi取值入手
1、随机值 (keyi的值是随机的,但是不推荐,随机值不好控制)
2、三数取中(在区间里面,左、右、中三个数取第二大的数到keyi里去)
注意:并不是keyi要换到这些位置,而是将取到值换到keyi指向的位置,因为我们本身的逻辑keyi就必须是在首元素位置✨✨
👉三数取中就可以避免上面的情况,数据左、右值以及中间值,三个数里面找中间值 ,然后将中间值换到首元素位置(逻辑不能变,keyi的位置初始情况在首元素✨);就可以保证排好序后,keyi的位置接近区间的中间
//优化:先三个数找中间:
int GetMin(int* a, int left, int right)
{int min = ((right - left) >> 1)+ left;if (a[min] < a[left]){if (a[min] > a[right]){return min;}else if (a[right]<a[left]){return right;}else{return left;}}else{if (a[min] < a[right]){return min;}else if (a[right] > a[left]){return right;}else{return left;}}}优化2:小区间优化
每次分割二分,以二叉树角度看,最后一层是2^(h-1)个节点,总节点是2^h,那么我发现倒数三层占递归比例挺大的哎,我能不能把这一段优化掉???不用递归了,降低栈溢出的风险🤔🤔
这里我们想到用一个时间复杂度为O(N^2)的排序来解决
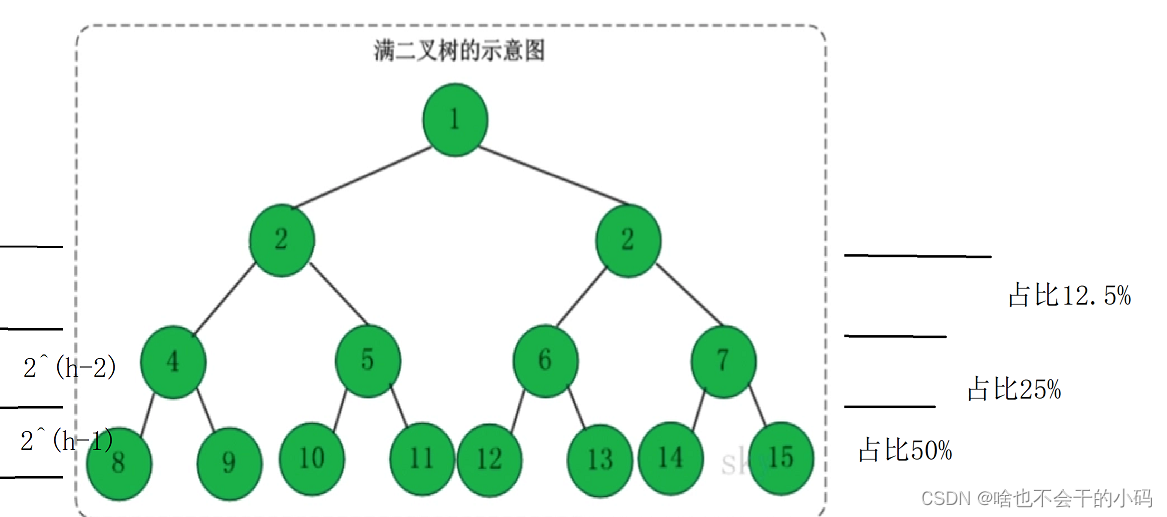
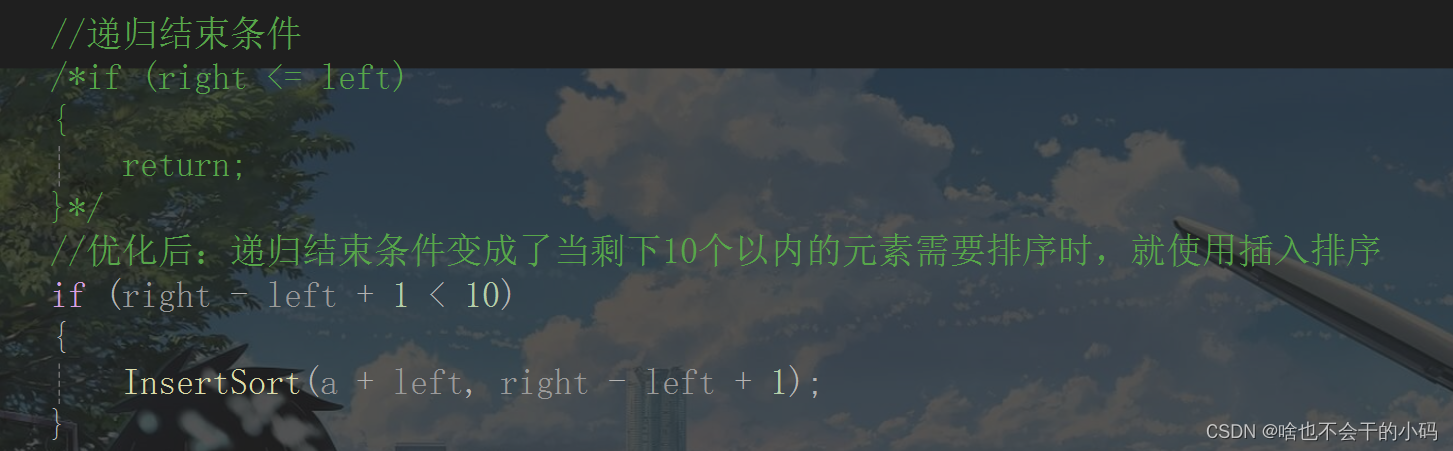
当区间元素个数小于10个时我就用一个插入排序 。修改一下递归条件即可递归结束条件即可
挖坑法: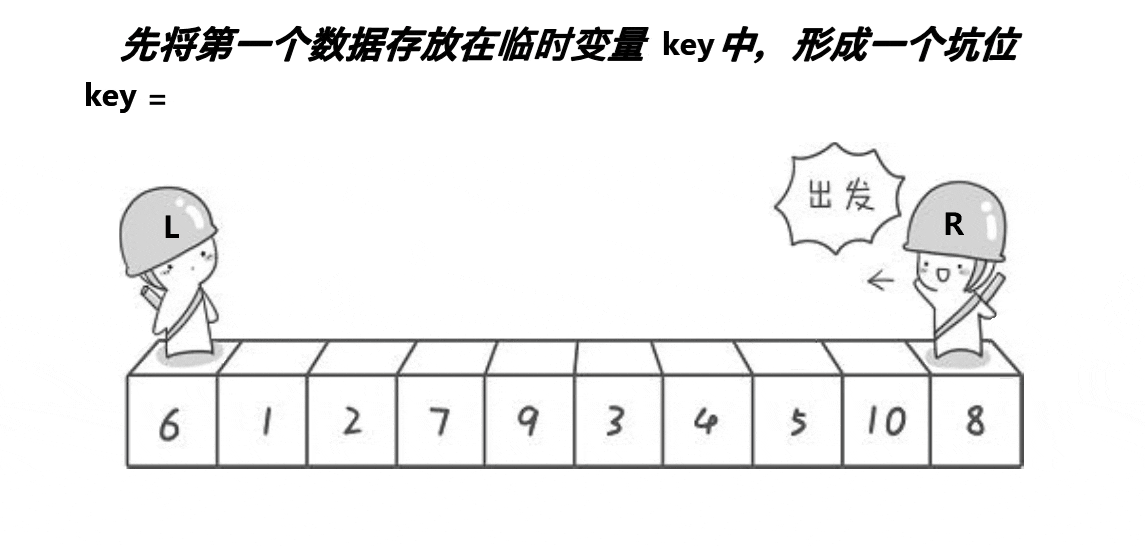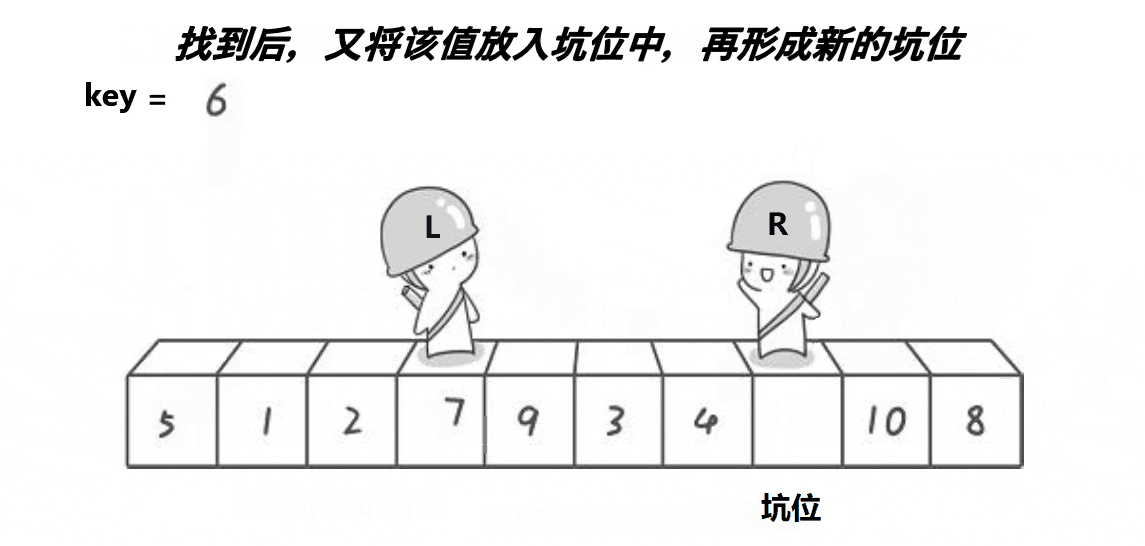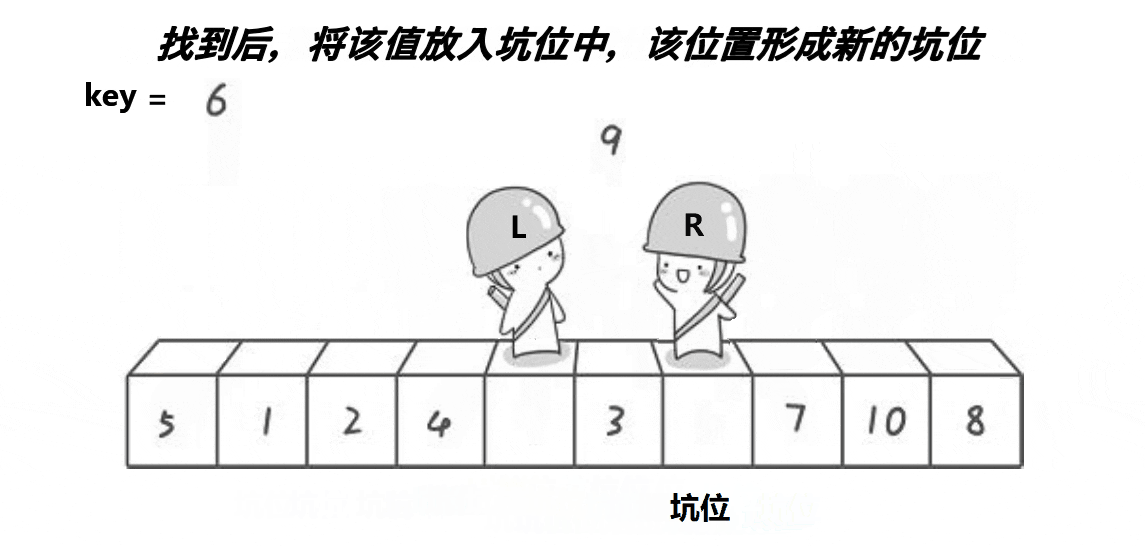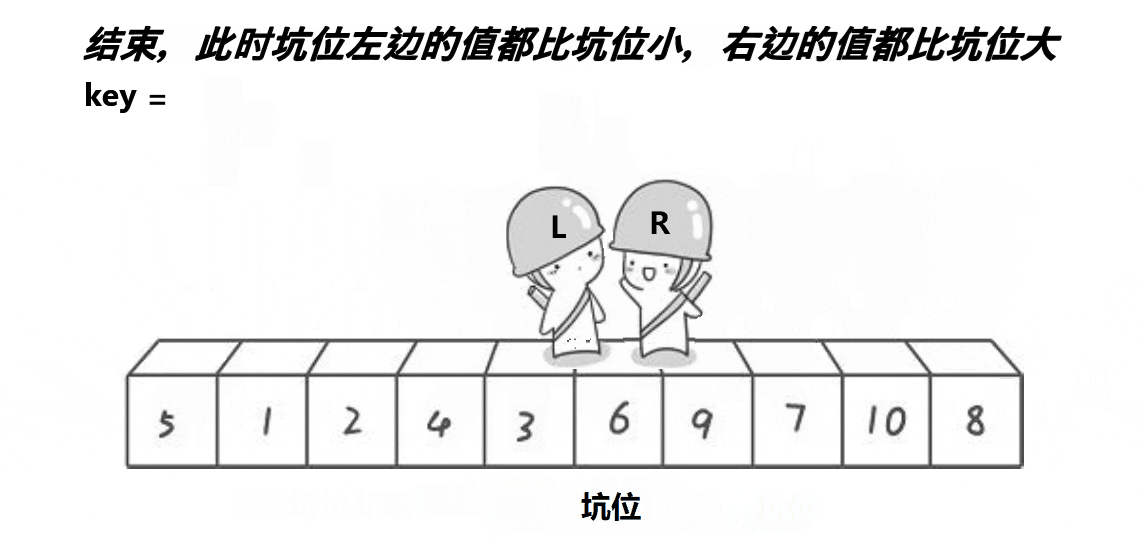
因为有些大佬认为Hoare的方法不易理解,就想到了挖坑法进行,这里用到了坑位
思路:key取出首元素,2个指针;begin指向首位置,end指向尾位置
✨占坑位的不能动,刚开始没有坑位的是end,当end走到比key小的位置,我们将end指向的元素放到begin指向的坑位,此时end变成坑位,end不动,begin走,找到比key大的元素,将begin指向的元素放到end指向的坑位;直到二者相遇,此时一起蹲坑,将key放到坑里面✨
前后指针法:
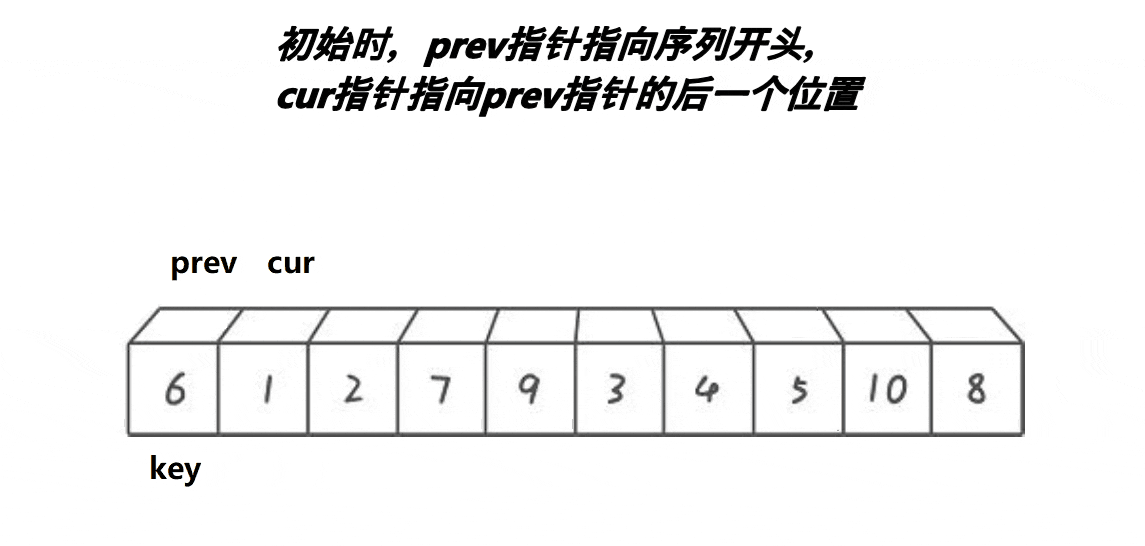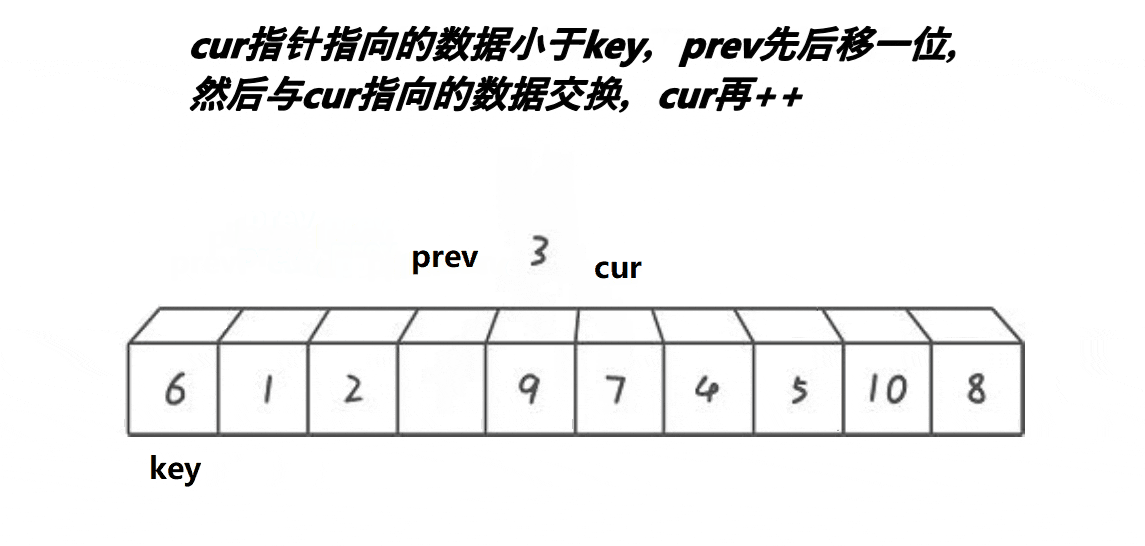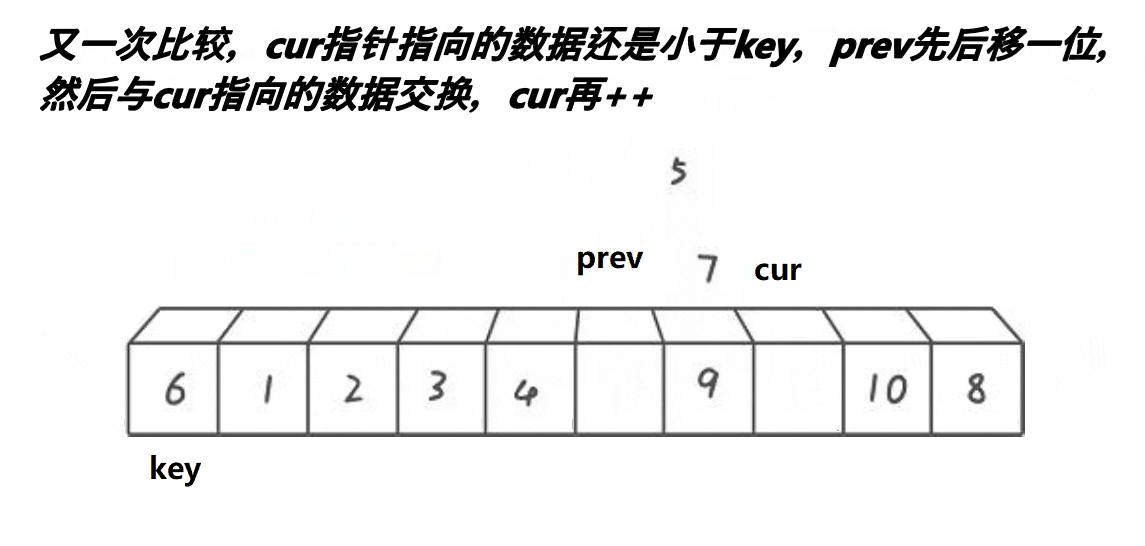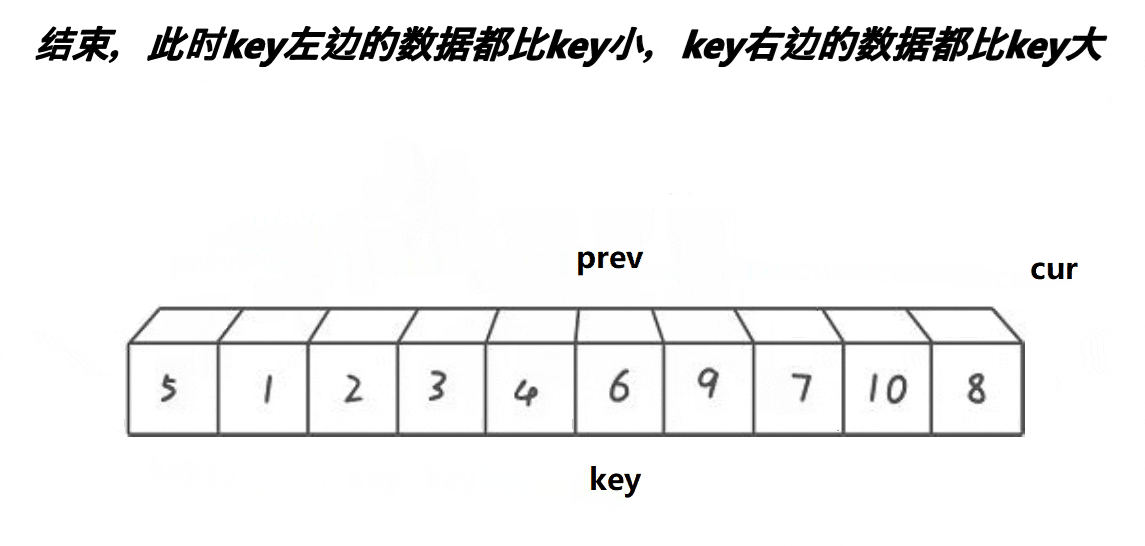
思路:2指针,起始位置:prev指向首元素,cur在第二个元素位置,先让cur走,若是cur指向数据比key小,则prev后移动一位,然后将cur指向的元素和prev指向的元素进行交换,当prev走过尾元素,也就是走出区间,将prev的值和key的值进行交换✨
总结:
🧑🎓后面2种写法都没有画过程,看动图其实就能很好的理解哦,很简单的,这里就不要考虑先走的问题了 直接规定好了。🐸当然啦✨✨三种方法的效率是一样的,后面的方法是为了更好的理解Hoare的思想,他们也就只是排序的写法改变了,方式都是一样的,逻辑没变✨
三、非递归思想:
✨我们通过递归可以发现,递归的是区间,对区间进行的修改,那么接下来以下面这个数组作为例子:👉
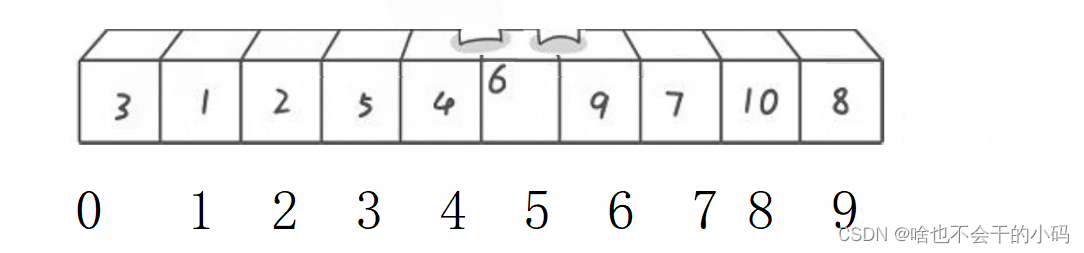
✨ 递归变非递归 其实就是将其变成迭代的思路
我们二叉树的前序遍历,就是根、左子树、右子树,那么我们的思路就是先遍历[0,9];然后遍历[0,4]再是[0,1] [3,4]等等,那么我们想到了创建一个栈来实现;利用先进后出的特点,可以将区间压进去,先入右区间,再入左,先出来的就是左区间
先入【0.9】 取出来进行排序
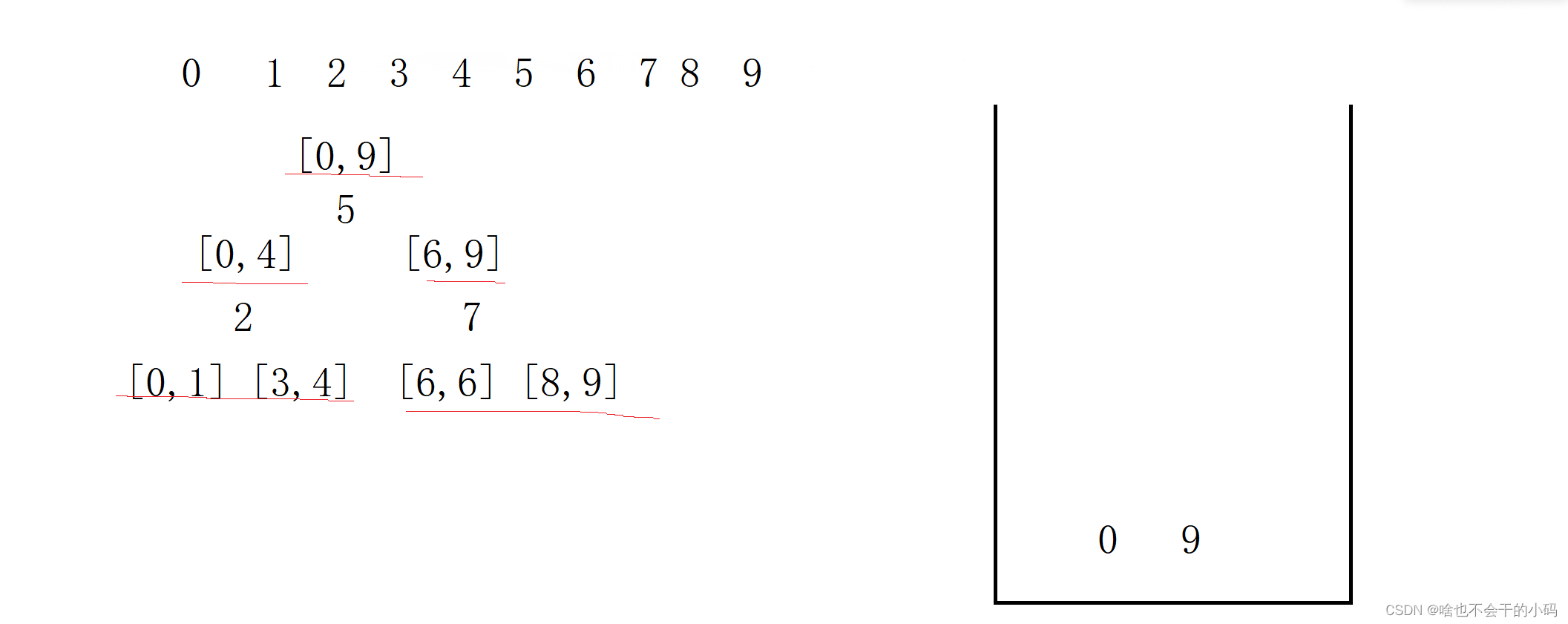
排完以后找到5,然后再入[6,9] 和 [0,4],此时区间变成2部分
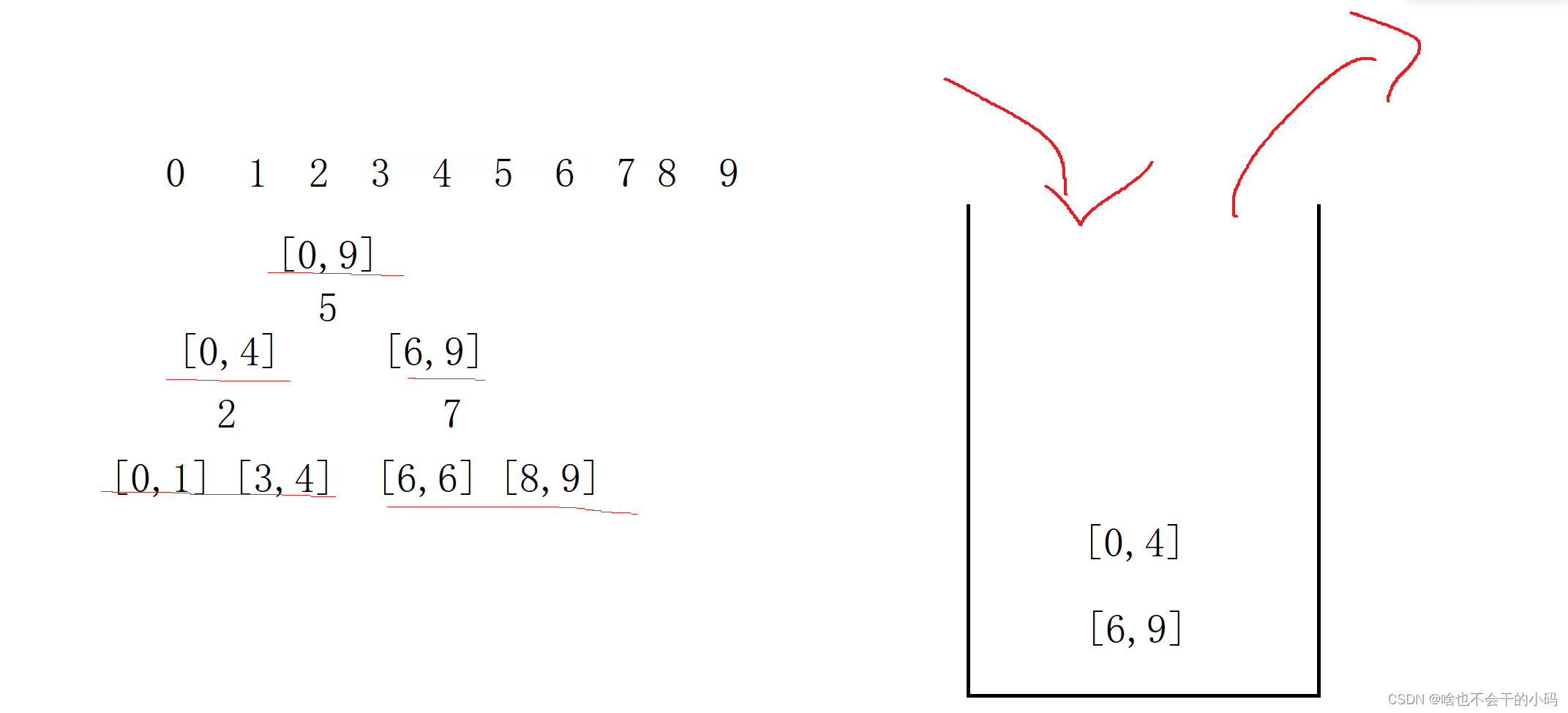
[0,4]出栈,交换后,此时以下标2进行分区间入栈

👉👉👉 是不是很好看懂,就是先动左区间再动右区间,处理一边再处理另一边,其实就是深度优先遍历么🐸🧑🎓
✨结束条件就是空栈结束喽
当然啦,你可以用队列实现,但是要注意队列是先进先出,它是一层一层的进行排的
排序的和递归里的排序方法一样,三种方法随便选一个都可以用,我们的栈就是来模拟实现先序遍历的过程
四、代码实现:
优化:三数取中,每种实现方法都需要用这个函数
//三数取中
int GetMin(int* a, int left, int right)
{int min = ((right - left) >> 1)+ left;if (a[min] < a[left]){if (a[min] > a[right]){return min;}else if (a[right]<a[left]){return right;}else{return left;}}else{if (a[min] < a[right]){return min;}else if (a[right] > a[left]){return right;}else{return left;}}}1、Hoare法:
void QuickSort1(int* a, int left, int right)
{//递归结束条件/*if (right <= left){return;}*///优化后:递归结束条件变成了当剩下10个以内的元素需要排序时,就使用插入排序if (right - left + 1 < 10){InsertSort(a + left, right - left + 1);}else {//3个取中int mid = GetMin(a, left, right);//将中的元素换到leftSwp(&a[mid], &a[left]);int keyi = left;int begin = left;int end = right;while (begin < end){//右边找小的,左边找大的while (a[end] >= a[keyi] && end > begin){end--;}while (a[begin] <= a[keyi] && end > begin){begin++;}//交换Swp(&a[begin], &a[end]);}Swp(&a[keyi], &a[begin]);QuickSort1(a, left, begin - 1);QuickSort1(a, end + 1, right);}
}2、挖坑法:
//挖坑法(有一个人要蹲坑)效率差不多
void QuickSort2(int* a, int left, int right){if (right - left + 1 < 10){InsertSort(a + left, right - left + 1);}else{int mid = GetMin(a, left, right);Swp(&a[left], &a[mid]);int keyi = a[left];int begin = left;int end = right;while (begin < end){//仍然是左边找大,右边找小while (begin < end && a[end] >= keyi){end--;}a[begin] = a[end];while (begin < end && a[begin] <= keyi){begin++;}a[end] = a[begin];}a[end] = keyi;QuickSort2(a, left, begin - 1);QuickSort2(a, end + 1, right);}}
3、前后指针法:
//前后指针法:
void QuickSort3(int* a, int left, int right)
{/*if (left >= right){return;}*/if (right - left + 1 < 10){//小于10个数据进行插入排序InsertSort(a + left, right - left + 1);}else{int mid = GetMin(a, left, right);Swp(&a[mid], &a[left]);int keyi = left;int prev = left;int cur = left + 1;//cur先走,找小的while (cur <= right){//若小于a[keyi]则prev后移一位 再交换if (a[cur] <= a[keyi]){prev++;Swp(&a[prev], &a[cur]);}cur++;}Swp(&a[prev], &a[keyi]);QuickSort3(a, left, prev - 1);QuickSort3(a, prev + 1, right);}
}
4、非递归:
#pragma once#include<stdio.h>
#include<stdbool.h>
#include<stdlib.h>
#include<assert.h>typedef int LTDataType;
//顺序表(栈)
typedef struct SL
{LTDataType* a;int top;int capacity;
}SL;
//入栈
void SLPush(SL* p,LTDataType x)
{//不能传NULL,判空;assert(p);if (p->top == p->capacity){//先判断是否为0,好进行扩容int newnode = p->capacity == 0 ? 4 : 2 * (p->capacity);//扩容;创建一个临时变量接收新的空间,成功在将其交给p->a;LTDataType* s = (LTDataType*)realloc(p->a,newnode * sizeof(LTDataType));if (s == NULL){perror("realloc");return;}p->a = s;p->capacity = newnode;}p->a[p->top] = x;//指向下一个数据地址p->top++;
}
//出栈(类似尾删)
void SLPop(SL* p)
{//是否为空assert(p);assert(p->top > 0);p->top--;
}
//初始化
void SLInit(SL* p)
{p->a = NULL;p->capacity = 0;//p->top = -1;//指向栈顶的数据p->top = 0;//指向栈顶的下一个数据
}
//销毁
void SLDestroy(SL* p)
{assert(p);free(p->a);p->a = NULL;p->capacity = p->top = 0;
}
//判空
bool SLEmpty(SL* p)
{//不能是空地址assert(p);//为0就是真(true),为1就是假(flase)return p->top == 0;
}
//数据个数
int SLsize(SL* p)
{int size = p->top;return size;
}
//取数据:
LTDataType SLPot(SL*p)
{assert(p);return p->a[p->top-1];
}//非递归,将递归变成迭代,最重要的是区间
void QuickSortNonR(int* a, int left, int right)
{SL pts;SLInit(&pts);SLPush(&pts,right);SLPush(&pts, left);while (!SLEmpty(&pts)){int begin = SLPot(&pts);SLPop(&pts);int end = SLPot(&pts);SLPop(&pts);int mid = GetMin(a, begin,end);Swp(&a[mid], &a[begin]);int keyi = begin;int prev = begin;int cur = begin + 1;//cur先走,找小的while (cur <= end){//若小于a[keyi]则prev后移一位 再交换if (a[cur] <= a[keyi]){prev++;Swp(&a[prev], &a[cur]);}cur++;}Swp(&a[prev], &a[keyi]);if (prev + 1 < end){SLPush(&pts, end);SLPush(&pts, prev + 1);}if (prev - 1 > begin){SLPush(&pts, prev-1);SLPush(&pts, 0);}}SLDestroy(&pts);}


相关文章:

【排序算法】快速排序
一、定义: 快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法(也叫Hoare排序),是一种基于分治的排序方。其基本原理是将待排序的数组通过一趟排序分成两个独立的部分,其中一部分的所有数据比另一部分的所有数…...

OS复习笔记ch7-2
页式管理 学过计组的同学都了解一点页式管理,就是将内存划分成较小的、大小固定的、等大的块。现在OS引入了进程的概念,那么为了匹配内存的分块,同样把进程也划分成同样大小的块。 这里区分两个概念 The chunks of a process are called p…...

4.通用编程概念
目录 一、变量与常量1.1 变量1.2 常量 二、遮蔽三、数据类型3.1 标量类型1. 整型2. 浮点型3. 布尔类型4.字符类型 3.2 复合类型1. 元组2. 数组 四、函数五、语句和表达式六、函数的返回值 一、变量与常量 1.1 变量 在Rust中默认的变量是不可变的,如果修改其值会导致…...

iBeacon赋能AR导航:室内定位技术的原理与优势
室内定位导航对于大型商场、机场、医院等复杂室内环境至关重要,它帮助人们快速找到目的地,提高空间利用率。AR技术通过将虚拟信息叠加在现实世界,提供直观导航指引,正在成为室内导航的新趋势,增强用户互动体验…...

【sklearn】【逻辑回归1】
学习笔记来自: 所用的库和版本大家参考: Python 3.7.1Scikit-learn 0.20.1 Numpy 1.15.4, Pandas 0.23.4, Matplotlib 3.0.2, SciPy 1.1.0 1 概述 1.1 名为“回归”的分类器 在过去的四周中,我们接触了不少带“回归”二字的算法…...
和 python 通过DoubleCloud的kafka进行线程间通信)
java(kotlin)和 python 通过DoubleCloud的kafka进行线程间通信
进入 DoubleCloud https://www.double.cloud 创建一个kafka 1 选择语言 2 运行curl 的url命令启动一个topic 3 生成对应语言的token 4 复制3中的配置文件到本地,命名为client.properties 5 复制客户端代码 对python和java客户端代码进行了重写,java改成…...
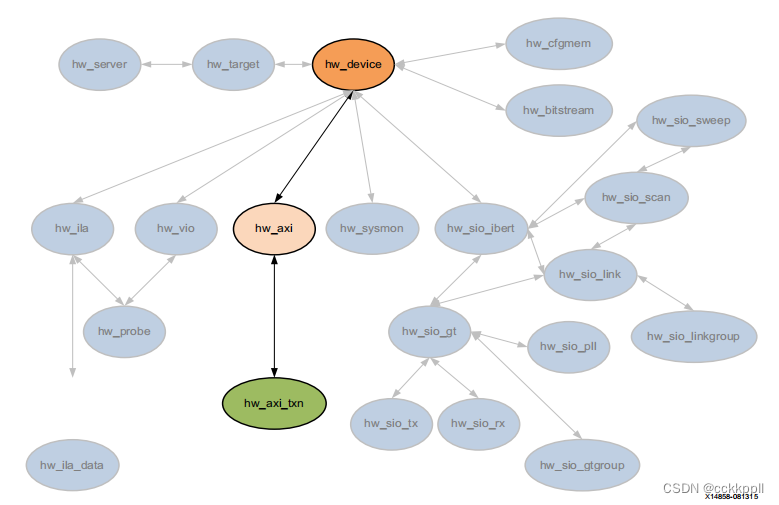
vivado DIAGRAM、HW_AXI
图表 描述 块设计(.bd)是在IP中创建的互连IP核的复杂系统 Vivado设计套件的集成商。Vivado IP集成器可让您创建复杂的 通过实例化和互连Vivado IP目录中的IP进行系统设计。一块 设计是一种分层设计,可以写入磁盘上的文件(.bd&…...

学习分享-为什么把后台的用户验证和认证逻辑放到网关
将后台的用户验证和认证逻辑放到网关(API Gateway)中是一种常见的设计模式,这种做法在微服务架构和现代应用中有许多优势和理由: 1. 集中管理认证和授权 统一的安全策略 在一个包含多个微服务的系统中,如果每个服务…...
27 ssh+scp+nfs+yum进阶
ssh远程管理 ssh是一种安全通道协议,用来实现字符界面的远程登录。远程复制,远程文本传输。 ssh对通信双方的数据进行了加密。 用户名和密码登录 密钥对认证方式(可以实现免密登录) ssh 22 网络层 传输层 数据传输的过程中是…...

LabVIEW液压伺服压力机控制系统与控制频率选择
液压伺服压力机的控制频率是一个重要的参数,它直接影响系统的响应速度、稳定性和控制精度。具体选择的控制频率取决于多种因素,包括系统的动态特性、控制目标、硬件性能以及应用场景。以下是一些常见的指导原则和考量因素: 常见的控制频率范…...
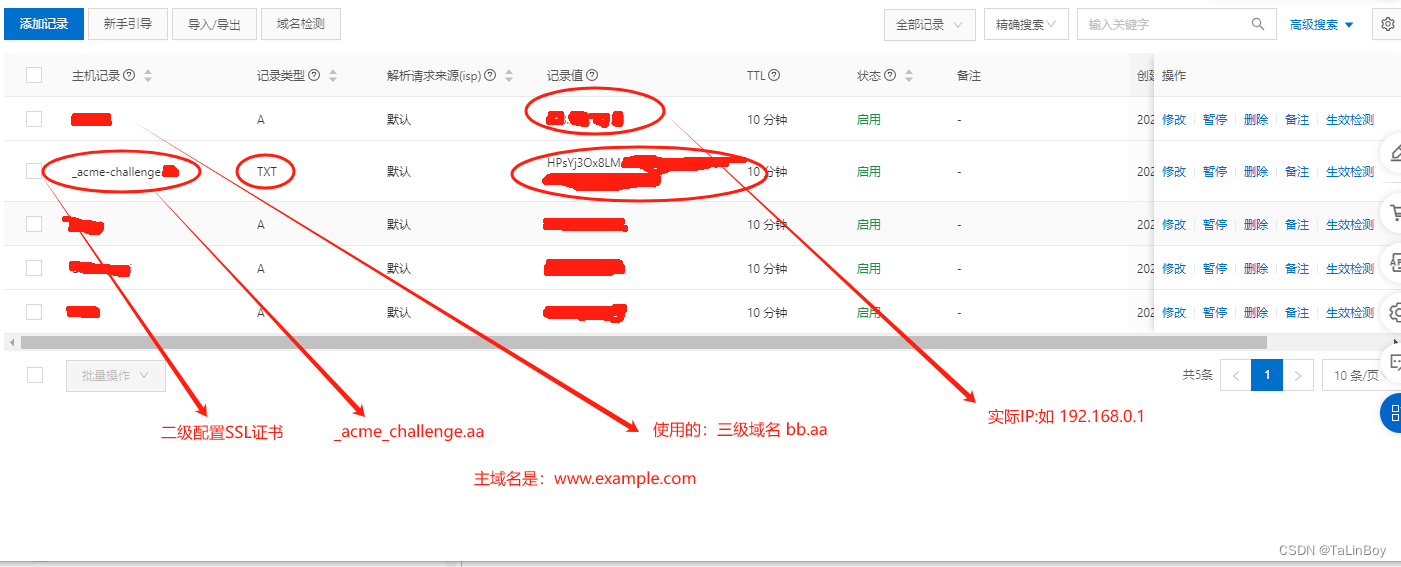
阿里云(域名解析) certbot 证书配置
1、安装 certbot ubuntu 系统: sudo apt install certbot 2、申请certbot 域名证书,如申请二级域名aa.example.com 的ssl证书,同时需要让 bb.aa.example.com 也可以使用此证书 1、命令:sudo certbot certonly -d “域名” -d “…...

Web LLM 攻击技术
概述 在ChatGPT问世以来,我也尝试挖掘过ChatGPT的漏洞,不过仅仅发现过一些小问题:无法显示xml的bug和错误信息泄露,虽然也挖到过一些开源LLM的漏洞,比如前段时间发现的Jan的漏洞,但是不得不说传统漏洞越来…...
)
Java等待异步线程池跑完再执行指定方法的三种方式(condition、CountDownLatch、CyclicBarrier)
Java等待异步线程池跑完再执行指定方法的三种方式(condition、CountDownLatch、CyclicBarrier) Async如何使用 使用Async标注在方法上,可以使该方法异步的调用执行。而所有异步方法的实际执行是交给TaskExecutor的。 1.启动类添加EnableAsync注解 2. 方法上添加A…...
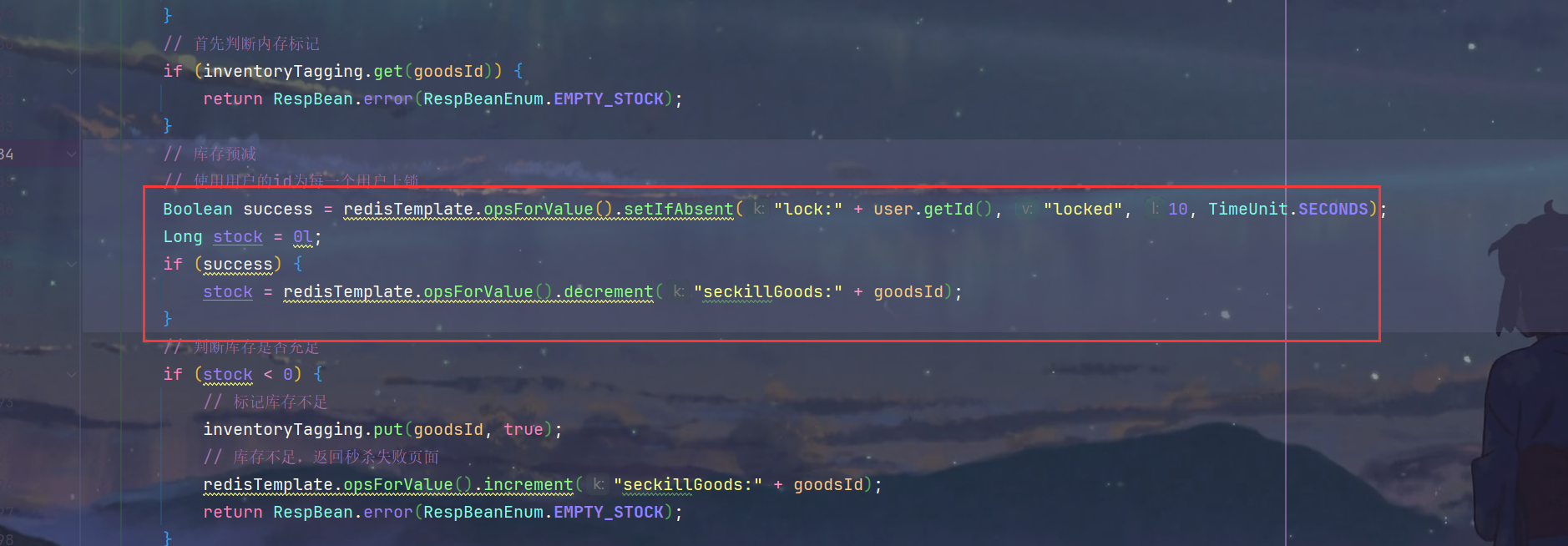
秒杀优化+秒杀安全
1.Redis预减库存 1.OrderServiceImpl.java 问题分析 2.具体实现 SeckillController.java 1.实现InitializingBean接口的afterPropertiesSet方法,在bean初始化之后将库存信息加载到Redis /*** 系统初始化,将秒杀商品库存加载到redis中** throws Excepti…...

48、Flink 的 Data Source API 详解
a)概述 本节将描述 FLIP-27 中引入的新 Source API 的主要接口。 b)Source Source API 是一个工厂模式的接口,用于创建以下组件。 Split EnumeratorSource ReaderSplit SerializerEnumerator Checkpoint Serializer 此外,Sou…...

深入解析Java扩展机制:SPI与Spring.factories
目录 Java SPI概述 1.1 什么是SPI?1.2 SPI的工作原理1.3 SPI的优缺点 SPI的应用 2.1 Java标准库中的SPI应用2.2 自定义SPI示例 Spring.factories概述 3.1 什么是spring.factories?3.2 spring.factories的工作原理3.3 spring.factories的优缺点 spring.f…...

Vue2之模板语法
文章目录 1.模板语法1.1 插值语法{{}}可以写什么1.2 指令语法1.2.1 指令概述1.2.2 v-bind指令1.2.3 v-model指令 1.模板语法 1.1 插值语法{{}}可以写什么 (1)在data中声明的 (2)常量 (3)合法的JavaScript…...
java基础练习题
1、一个".java"源文件中是否可以包括多个类?有什么限制? 可以包含多个类。但是只有一个类可以声明为public,且要求声明为public的类的类名与源文件名相同。 2、java的优势? a、跨平台性 b、安全性高 c、简单性 d、…...
的事件监听)
unity中通过实现底层接口实现非按钮(图片)的事件监听
编写监听脚本 PEListenter 继承自MonoBehaviour类,并实现了IPointerDownHandler、IPointerUpHandler和IDragHandler接口,按照需求定义需要接收事件(鼠标按下、抬起、拖拽)的回调函数 //监听类(需要挂载在物体上面&am…...

重庆耶非凡科技有限公司的选品师项目加盟靠谱吗?
在当今电子商务的浪潮中,选品师的角色愈发重要。而重庆耶非凡科技有限公司以其独特的选品师项目,在行业内引起了广泛关注。对于想要加盟该项目的人来说,项目的靠谱性无疑是首要考虑的问题。 首先,我们来看看耶非凡科技有限公司的背…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...