最短路径——迪杰斯特拉与弗洛伊德算法
一.迪杰斯特拉算法
首先对于最短路径来说:从vi-vj的最短路径,不用非要经过所有的顶点,只需要找到路径最短的路径即可;
那么迪杰斯特拉的算法:其实也就与最小生成树的思想类似,找到较小的,然后更新;
首先将dist(路径)长度初始化为两个点之间边的权值,而如果不能一次到达,就是INIFINITY
而迪杰斯特拉算法就是:加点,如果加上中转点之后,再判断此时的最短路径长度,如果此时i-j-k的路径长度小于i-k的,那么此时顶点vi的最短路径就修改为中转路径长度;并且最终将找到的最小路径的终点加入到集合S中,直至所有的顶点都在S中就找到了V0到所有其他顶点的最短路径;
就是判断,更新,但最中间的过程有点麻烦,条件判断也太多;像比于书中的用链表来表示集合的加点,加边,还是实验题中的利用标志数组更为容易,将标志数组变为0/1,这样就不用那么麻烦!!!
下面给出关于迪杰斯特拉算法的完整代码:
#define MAX_VERTEX_NUM 100
#define INFINITY 32768//表示极大值typedef struct
{int vex1;int vex2;int adj_weight;
}Arc;typedef int VertexData;typedef struct ArcNode
{int adj;
}ArcNode;typedef struct
{VertexData vertex[MAX_VERTEX_NUM];ArcNode arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM];int vexnum, arcnum;
}AdjMatrix;//邻接矩阵创建有向图
void CreateDN(AdjMatrix* G,int m)
{int i; int j;int** arr = (int**)malloc(m* sizeof(int*));for (i = 0; i <m; i++){arr[i] = (int*)malloc(m* sizeof(int));}for (i = 0; i < m; i++){for (j = 0; j < m; j++){scanf("%d", &arr[i][j]);}}for (i = 0; i < m; i++){for (j = 0; j <m; j++){if (arr[i][j] != 0){G->arcs[i][j].adj = arr[i][j];}else{G->arcs[i][j].adj = INFINITY;}}}G->vexnum = m;for (i = 0; i <m; i++){free(arr[i]);}free(arr);
}void PrintAdj(AdjMatrix* G)
{for (int i = 0; i <G->vexnum; i++){for (int j = 0; j < G->vexnum; j++){printf("%d ", G->arcs[i][j].adj);}printf("\n");}
}typedef int** PathMatrix;
typedef int* ShortPathTable;
//第五题//path用于保存路径信息,dist用来表示最短路径长度,即边的权值
void ShortestPath_DIJ(AdjMatrix* G, int v0, PathMatrix P, ShortPathTable D)
{int i = 0, j, w, v, min;int final[MAX_VERTEX_NUM];for (v = 0; v < G->vexnum; v++){final[v] = 0;D[v] = G->arcs[v0][v].adj;//从源点到点v的距离,for (w = 0; w < G->vexnum; w++){P[v][w] = 0;//从源点到w点的最短路径是否经过v点//到所有点都设置为不可到达?设置空路径}if (D[v] < INFINITY)//那么初始化的时候,要再加一个附加条件,如果矩阵输入为0,则INFINITY{P[v][v0] = 1; P[v][v] = 1;//小于的话,就存在直接到达的路径//那为什么还要经过v?为什么P???对于矩阵P的意义还是没理解}//从源点到顶点v0中v是中间要经过的}D[v0] = 0;//v0到v0的距离为0;final[v0] = 1;//到自身肯定已经遍历完成//for (i = 1; i < G->vexnum; i++)//这里只代表循环次数,i没有实际的意义//表示剩余的n-1个节点{min = INFINITY;for (w = 0; w < G->vexnum; w++)//有的可能从源点到达不了w,所以一直循环//此时一直循环:{if (!final[w])//说明还没有找到从源点到w的路径{if (D[w] < min){v = w;//此时将v更新为w(不要只注意前两行的,还有后面的//为什么要更新为w呢?//此时v在第一步肯定是要更新的,//然后v就是代表除了v0以外的节点,那么此时也就是从v0到v的已经找到路径min = D[w];}}}//上述过程就是在找到剩下的节点中到达v0的最小的距离final[v] = 1;//见上面的解释//此时就是最终的v才是最后真正访问的w//将final[v]更新以后,他就不再参与后面的运算!就不会与min进行比较//那么就是找出剩余的最短的路径——这就体现了按照路径长度递增的次序for (w = 0; w < G->vexnum; w++){if (!final[w] && (min + G->arcs[v][w].adj) < D[w])//说明找到了//一个更短的路径,这个才是更新路径的判断条件{D[w] = min + G->arcs[v][w].adj;//更新最短路径for (j = 0; j < G->vexnum; j++){P[w][j] = P[v][j];//P有什么用???}P[w][w] = 1;//说明已经完成了所有的遍历?因为在循环中,所有的都设置为1了}}}for (i = 0; i < G->vexnum; i++){if (i != v0){if (D[i] < INFINITY){printf("%d ", D[i]);}else{printf("-1 ");}}}
}int main()
{AdjMatrix G;//G = (AdjMatrix*)malloc(sizeof(AdjMatrix));int m, n;scanf("%d %d",&m, &n);CreateDN(&G, m);//PrintAdj(G);PathMatrix p;p = (int**)malloc(G.vexnum*sizeof(int*));for (int i = 0; i < m; i++){p[i] = (int*)calloc(G.vexnum,sizeof(int));}ShortPathTable D;D = (int*)malloc(m*sizeof(int));for (int i = 0; i <m; i++){D[i] =INFINITY;}//别忘了把n加1;ShortestPath_DIJ(&G, n, p, D);return 0;
}二.弗洛伊德算法
若是求任意两个顶点之间的最短路径,就可以将每一个顶点作为源,多次调用迪杰斯特拉算法就可以找到任意两个顶点之间的最短路径,而利用弗洛伊德算法:就可以直接利用三重循环求出任意两点间的最短路径;
弗洛伊德算法最重要的就是要理解三重循环:

首先理解一下path:这个数组是存放i->j的最短路径的前驱结点,也就是距离j结点的最近的一个结点;
这时候:会有一个疑问,只存放一个前驱结点,那如何打印出路径上的所有结点呢?
有这个疑问就是没有理解三重循环的含义:假设i->j的前驱节点path[i][j]=p;
而p也是属于其他所有结点中的一个结点,那么自然也会有从i->p的最短路径,假设i->p的最短路径的前驱结点为m,那么i....m->p->j;也就是说,m也是属于从i->j的最短路径上的结点(因为单个值最小,所有的单个值的和肯定也最小,m,是保证从i->p的路径最短的点,那么m理应属于i->j的最短路径)以此类推直到找到距离i最近的前驱节点;此时也就找出了从顶点i到达任意所有其他结点的最小路径;而i->j的路径也就在这个过程中能够全部得出来!
综上所述:三层循环得本质我们就可以得到:i,j两层循环是作为二维数组的下标i,j;而表示从结点i到达结点j,而k则是可以作为前驱节点(中间结点)因为前驱节点肯定是在所有结点中间的,所以这层k的循环就代表这个意思;最终就能够找到所有的由顶点i到其他所有结点的最小路径;
而在打印路径的时候,根据上面的理解,path[i][j]只代表一个结点,那难道就只能打印一个结点吗?
根据上面的理解,我们既然可以找到i->j的前驱节点k,那么自然也能找到i->k的前驱结点,以此类推,递归下去,就能找到i->j的路上的所有其它的结点;
所以打印的过程是个递归的过程;
相关文章:

最短路径——迪杰斯特拉与弗洛伊德算法
一.迪杰斯特拉算法 首先对于最短路径来说:从vi-vj的最短路径,不用非要经过所有的顶点,只需要找到路径最短的路径即可; 那么迪杰斯特拉的算法:其实也就与最小生成树的思想类似,找到较小的,然后…...
6.7.11 一种新的迁移学习方法可提高乳房 X 线摄影筛查中乳腺癌的诊断率
分割是一种将图像分割成离散区域的技术,以便将感兴趣的对象与周围环境分开。为了制定治疗计划,分割可以帮助医生测量乳房中的组织量。 二元分类问题的目的是将输入数据分为两组互斥的数据。在这种情况下,训练数据根据要解决的问题以二进制格…...
【Proteus8.16】Proteus8.16.SP3.exe的安装包,安装方法
下载: 链接:https://pan.baidu.com/s/14ZlETF7g4Owh8djLaHwBOw?pwd2bo3 提取码:2bo3 管理员打开proteus8.16.SP3.exe一路装就行了,许可证选Licence2.lxk,点安装后关闭,然后继续装完。 然后打开Patch-Proteus-8.16-…...
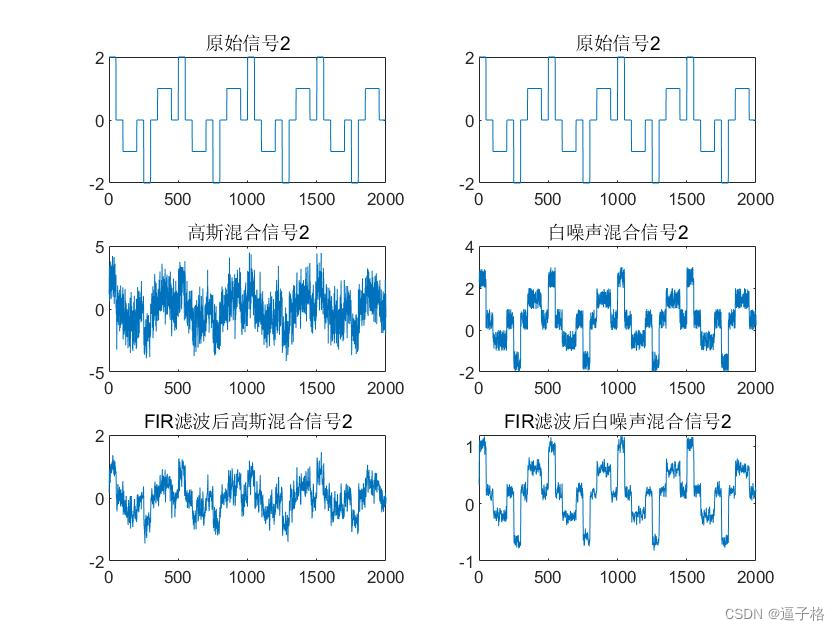
17、matlab实现均值滤波、中值滤波、Butterworth滤波和线性相位FIR滤波
1、创建信号 1)创建正余弦信号、噪声信号和混合信号 原始正余弦信号公式:Signal1 sin(2*pi*20* t) sin(2*pi*40* t) sin(2*pi*60* t) 高斯分布的白噪声:NoiseGauss [randn(1,2000)] 均匀分布的白噪声:[rand(1,2000)] 正余弦…...

【Autopilot】没有自动添加本地管理员的问题处理
【问题】某公司选用了D记的笔记本电脑,约定出厂就预配置好Autopilot,当时向D记提供了三个信息: 1. M365的租户ID 2. 公司域名信息 3. Group Tag (某公司为跨国公司,通过Group Tag来区分国家,比如CHN-中国,L…...

【C#学习笔记】属性和字段
文章目录 前言属性和字段的区别字段访问修饰符和关键字定义变量类型的定义变量命名变量的赋值 属性 不同的使用情况 前言 最近在工作的过程中常常会觉得自己在程序设计方面的能力还是有欠缺。例如一直对于变量的声明感到不足,在工作中为了图方便总是直接public定义…...

最佳实践的实践 - API 不应将 HTTP 重定向到 HTTPS
原文:jviide - 2024.05.23 TL;DR: 与其将 API 调用从 HTTP 重定向到 HTTPS,不如让失败显而易见。要么完全禁用 HTTP 接口,要么返回明确的 HTTP 错误响应,并撤销通过未加密连接发送的 API 密钥。遗憾的是,许多知名的 A…...

四种跨域解决方案
文章目录 1.引出跨域1.基本介绍2.具体演示1.启动之前学习过的springboot-furn项目2.浏览器直接访问 [localhost:8081/furns](http://localhost:8081/furns) 可以显示信息3.启动前端项目,取消请求拦截器,这样设置,就会出现跨域4.跨域原因 2.跨…...
移动端投屏到大屏幕的操作详解
如果你懒得折腾电脑、电视或其他大屏设备上的影视软件安装及配置,可以选择直接在手机端上将影片投屏到电脑、电视或其他大屏设备上,这里给大家分享三种手机投屏的方法。 系统自带的投屏功能 不管是安卓、鸿蒙还是苹果操作系统,都自带了无线…...

【环境搭建】3.阿里云ECS服务器 安装Redis
在阿里云的 Alibaba Cloud Linux 3.2104 LTS 64位系统上安装 Redis 可以通过以下步骤完成: 1.更新系统软件包: 首先,更新系统软件包以确保所有软件包都是最新的: sudo yum update -y2.安装编译工具和依赖项: Redis…...

动态语言的开源编译器汇总
对于动态语言而言,我们通常不会使用传统意义上的“编译器”,因为动态语言往往是在运行时解释执行的,或者被转换为中间形式(如字节码),再由虚拟机执行。不过,为了性能考虑,现代动态语…...

Linux防火墙配置001
Linux防火墙主要用于控制网络流量,保护系统安全。在Linux中,有几种不同的防火墙管理工具,其中最常见的是iptables和firewalld。本章主要讲述如何关闭防火墙。 操作系统: CentOS Stream 9 操作步骤: 关闭防火墙&…...
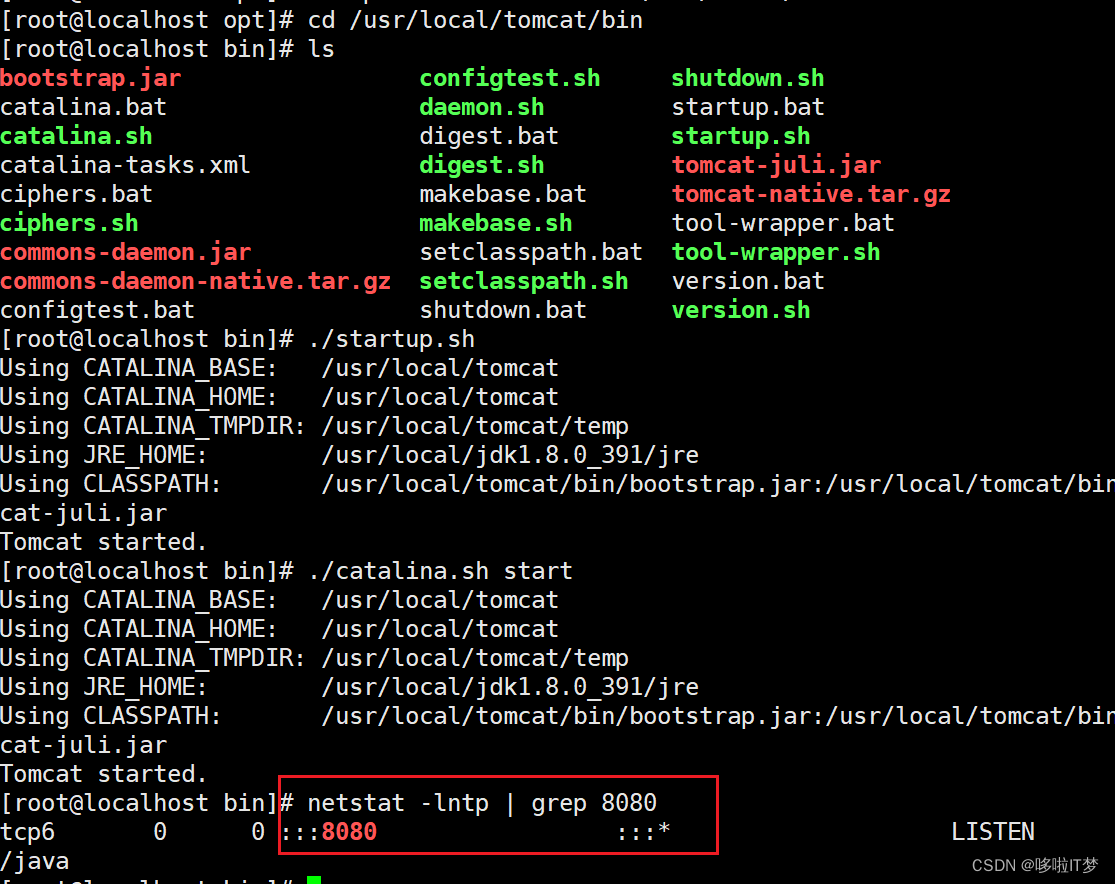
Tomcat概述及部署
目录 一.Tomcat概述 1.介绍 2.使用场景 3.组件构成 4.组件结构 5.请求过程 二.Tomcat部署 1.关闭防火墙 2.下载安装JDK 3.安装启动tomcat 4.部署虚拟主机 4.1.创建 xy101 和 xy102 项目目录和文件 4.2.修改 Tomcat 主配置文件 server.xml 一.Tomcat概述 1.介绍 …...
[Vue3:Vite构建项目]:安装router实现登录页面路由跳转
文章目录 一:前置依赖查看依赖安装vite npm create vitelatest sys-instruction-0607 --template vue-ts安装路由:npm install vue-router4安装elementUI:npm install element-plus --save 二:配置文件:viewsÿ…...

概率论与数理统计,重要知识点——全部公式总结
二、一维随机变量及其分布 五个分布参考另外一篇文章 四、随机变量的数字特征 大数定理以及中心极限定理 六、数理统计...

Spring系列-SpringMvc父子容器启动原理解析
1、Spring整合SpringMVC 特性: 说到Spring整合SpringMVC唯一的体现就是父子容器: 通常我们会设置父容器(Spring)管理Service、Dao层的Bean, 子容器(SpringMVC)管理Controller的Bean .子容器可以访问父容器的Bean, 父容器无法访…...

[ssi-uploader插件]解决如何接收服务器返回数据+修改参数名称
前言 ssi-uploader是一款非常好用的多文件上传插件,源码是开源的,在github上面即可下载: https://github.com/ssbeefeater/ssi-uploader 但是源码有些微小的不足,今天我们解决两点问题: 上传文件完成后,…...
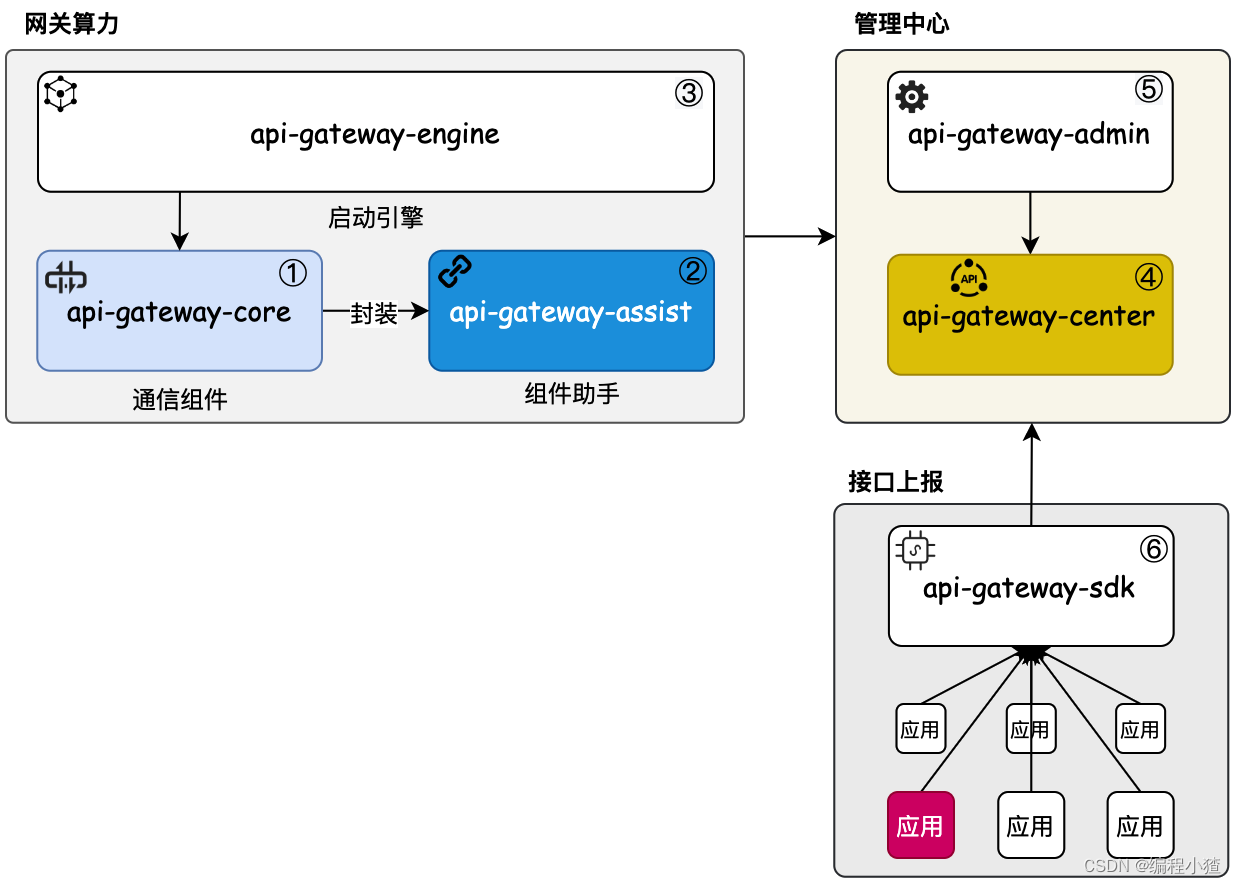
InfiniGate自研网关实现思路七
25.网关Nginx负载模型配置 通过模拟多个HTTP服务配置到 Nginx 做负载均衡,以学习API网关负载的配置和使用 API 网关是用于支撑分布式 RPC 接口协议转换提供 HTTP 调用的一套服务,那么 API 网关系统就需要可横向扩展来满足系统的吞吐量诉求。所以这里需…...

277 基于MATLAB GUI火灾检测系统
基于MATLAB GUI火灾检测系统,可以实现图片和视频的火苗检测。火焰识别的三个特征:1个颜色特征,2个几何特征颜色特征:HSV颜色空间下,对三个通道值进行阈值滤波,几何特征1:长宽比,几何…...
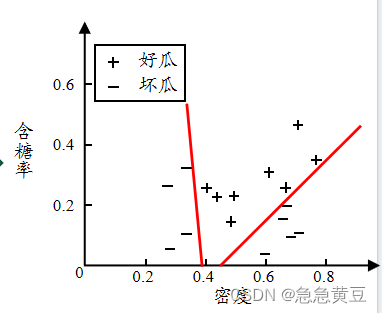
【西瓜书】4.决策树
1 递归返回情况 (1)结点包含样本全为同一类别 (2)属性集为空,没有属性可供划分了 或 有属性,但是在属性上划分的结果都一样 (3)结点为空结点 **结束时判定该结点的类别遵循如下规则&…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
