支持向量机(SVM): 从理论到实践的指南(1)
支持向量机(SVM)被誉为数据科学领域的重量级算法,是机器学习中不可或缺的工具之一。SVM以其优秀的泛化能力和对高维数据的管理而备受推崇。本文旨在梳理SVM的核心概念以及其在实际场景中的应用。
SVM的核心理念
SVM专注于为二分类问题找到最佳决策边界,即超平面,该平面能最大化两类数据之间的空隙或间隔。线性SVM假设用一个直线(或高维空间中的超平面)足以有效地分隔数据。当遇到重叠或杂乱无章散布的数据时,软间隔SVM允许某些点位于错误的边界一侧,这通过引入松弛变量与罚项系数C来实现,从而提供一个稳健的平衡方案。
算法实现
SVM通过转化优化问题为其对偶形式并使用拉格朗日乘子法来解决。这不仅简化了求解过程,还能自然地加入核技巧(Kernel trick)来处理非线性可分的数据集。
详细算法描述>>>>
一个经典案例
为了具体说明SVM的应用,我们考虑了一个著名的数据集。
- 鸢尾花分类:鸢尾花数据集由三个品种的鸢尾花构成,每一种都有50个样本和4个特征。对于二分类任务,我们专注于将Setosa从Versicolour中区分出来。
实践应用
利用MindOpt APL,一种强大的代数建模语言和求解器,我们可以更高效地构建和解决SVM优化问题。在训练阶段,算法学习数据的模式,并找到分隔不同类别的最优决策边界。一旦模型确定,我们便可用其做出预测并评估其在未见数据上的性能。
clear model;####################################################
#
# Vectorization Modeling Example
# Linear SVM
#
####################################################option modelname svm_02; #定义存储文件名# ----------建模--------Start----
# svm_02.mapl# 1.读取iris的用于构建SVM模型的训练数据
param data_dir = "./data/iris_data-train.csv";
param X = read_csv( data_dir, use_col="0,1,2,3",skip=1);
param y = read_csv( data_dir, use_col=4,skip=1);
param dataNum = X.row;
param dataDim = X.col;
print "总共有{}个数据,每个数据有{}维"%dataNum,dataDim;# 2.LinearSVM问题建模
param C_rho = 0.2;
print "Param C is :{}"%C_rho;print "Start modeling-------";var w(dataDim) >= -1 <= 1; # Bounded Model Parameter
var b; #
var eps(dataNum) >= 0;minimize 1/2 * w' * w + C_rho * sum(eps); #'是转置,目标函数subto constraint:eps >= 1 - (X*w +b).*y; #注意是向量化建模,因此相当于多条维度的约束# 3.调用求解器求解
print "Start solving-------";
option solver mindopt;
solve;# 4. 超平面的w取值
print "- Optimal w is:";
print w;
print "- Optimal b is:";
print b;
print "- eps is:";
forall { i in 0..dataNum-1 with eps[i] > 0.001}print " - eps[{}] = {} "%i,eps[i];param obj_total_loss = 1/2 * w' * w + C_rho * sum(eps); #'是转置
print "- obj of total loss is : {}"%obj_total_loss;# 5.验证并分析结果print "";
print "验证结果:-----";param correctNum = sum{i in 0..dataNum-1} if((sum{j in 0..dataDim-1}w[j]*X[i, j]) +b )* y[i] > 0 then 1 else 0 end;
param precision = correctNum / dataNum;
print "- Precision for train data is : {:.2f}" % precision;#
print "";
print "导入测试数据验证效果:-----";param data_dir_test = "./data/iris_data-test.csv";
param X_test = read_csv( data_dir_test, use_col="0,1,2,3",skip=1);
param y_test = read_csv( data_dir_test, use_col=4,skip=1);
param dataNum_test = X_test.row;
param dataDim_test = X_test.col;
print "- 总共有{}个数据,每个数据有{}维"%dataNum_test,dataDim_test;print "|测试数据ID|实际标签|SVM预测标签是|";
print "|--|--|--|";
forall {i in 0..dataNum_test-1}
print "|{}|{}|{}|"%i,y_test[i], if((sum{j in 0..dataDim_test-1}w[j]*X_test[i, j]) +b ) > 0 then 1 else -1 end;
运行上述代码结果如下:
总共有80个数据,每个数据有4维
Param C is :0.2
Start modeling-------
Start solving-------
Running mindoptampl
wantsol=1
MindOpt Version 1.2.1 (Build date: 20240428)
Copyright (c) 2020-2024 Alibaba Cloud.Start license validation (current time : 29-APR-2024 17:51:11).
License validation terminated. Time : 0.007sModel summary.- Num. variables : 85- Num. constraints : 80- Num. nonzeros : 480- Bound range : [1.0e+00,1.0e+00]- Quad. bound range : [1.0e+00,1.0e+00]- Objective range : [2.0e-01,2.0e-01]- Quad. obj. range : [1.0e+00,1.0e+00]- Matrix range : [1.0e-01,7.0e+00]Presolver started.
Presolver terminated. Time : 0.000sInterior point method started.Iter PrimObj DualObj PrimFea DualFea GapFea Mu Time0 +1.56581101e+01 -1.06624290e+01 2.0e-01 2.6e-01 2.5e+00 6.2e-01 0.02s1 +8.56566249e+00 -7.16779185e-01 5.4e-04 7.6e-03 9.3e+00 6.5e-02 0.04s2 +9.75513434e-01 +2.94267093e-01 2.7e-05 1.4e-03 6.8e-01 4.1e-03 0.05s3 +5.98630319e-01 +4.50898225e-01 4.2e-06 1.5e-04 1.5e-01 8.9e-04 0.05s4 +5.12227038e-01 +4.88329845e-01 1.1e-08 1.2e-03 2.5e-02 1.5e-04 0.05s5 +5.04653750e-01 +5.01437631e-01 9.7e-10 2.0e-04 3.2e-03 1.9e-05 0.06s6 +5.02835294e-01 +5.02808740e-01 2.7e-12 5.4e-07 2.7e-05 1.6e-07 0.06s7 +5.02821164e-01 +5.02821090e-01 7.1e-15 1.5e-09 7.3e-08 4.4e-10 0.06s8 +5.02821125e-01 +5.02821124e-01 1.9e-16 4.1e-12 2.0e-10 1.2e-12 0.06s
Terminated.- Method : Interior point method.- Primal objective : 5.0282112458779E-01- Dual objective : 5.0282112438583E-01- Num. threads : 4- Num. iterations : 8- Solver details : Solver terminated with a primal/dual optimal status.Interior point method terminated. Time : 0.046sOPTIMAL; objective 0.50
0 simplex iterationsCompleted.
- Optimal w is:
[[-0.16610],[ 0.35465],[-0.75422],[-0.32403]]
- Optimal b is:
2.038087831121987
- eps is:- eps[23] = 0.08284647160625058 - eps[24] = 0.05118542249112839 - eps[47] = 0.26241815907236044 - eps[69] = 0.04962685713002854
- obj of total loss is : 0.5028211245877855验证结果:-----
- Precision for train data is : 1.00导入测试数据验证效果:-----
- 总共有20个数据,每个数据有4维
|测试数据ID|实际标签|SVM预测标签是|
|--|--|--|
|0|1|1|
|1|1|1|
|2|1|1|
|3|1|1|
|4|1|1|
|5|1|1|
|6|1|1|
|7|1|1|
|8|1|1|
|9|1|1|
|10|-1|-1|
|11|-1|-1|
|12|-1|-1|
|13|-1|-1|
|14|-1|-1|
|15|-1|-1|
|16|-1|-1|
|17|-1|-1|
|18|-1|-1|
|19|-1|-1|
结果
上面的程序运行结果如下:
其中,小数后几位是精度影响,每次会有变化,不影响结果。
总共有80个数据,每个数据有4维
Param C is :0.2
……
- Optimal w is: [[-0.16610], [ 0.35465], [-0.75422], [-0.32403]]
- Optimal b is: 2.038087831122001
- eps is:
- eps[23] = 0.08284647160625147
- eps[24] = 0.051185422491125426
- eps[47] = 0.26241815907236443
- eps[69] = 0.049626857130028075
- obj of total loss is : 0.5028211245877853
验证结果:-----
- Precision for train data is : 1.00
导入测试数据验证效果:-----
- 总共有20个数据,每个数据有4维
-
测试数据ID 实际标签 SVM预测标签是 0 1 1 1 1 1 2 1 1 3 1 1 4 1 1 5 1 1 6 1 1 7 1 1 8 1 1 9 1 1 10 -1 -1 11 -1 -1 12 -1 -1 13 -1 -1 14 -1 -1 15 -1 -1 16 -1 -1 17 -1 -1 18 -1 -1 19 -1 -1
可以看到,对于这份数据,计算的超平面能很好地进行二分类,在测试集合上也有100%的正确率,证实了SVM在实际问题中的有效性。
相关文章:
: 从理论到实践的指南(1))
支持向量机(SVM): 从理论到实践的指南(1)
支持向量机(SVM)被誉为数据科学领域的重量级算法,是机器学习中不可或缺的工具之一。SVM以其优秀的泛化能力和对高维数据的管理而备受推崇。本文旨在梳理SVM的核心概念以及其在实际场景中的应用。 SVM的核心理念 SVM专注于为二分类问题找到最…...

万字长文|OpenAI模型规范(全文)
本文是继《OpenAI模型规范概览》之后对OpenAI Model Spec的详细描述,希望能对各位从事大模型及RLHF研究的朋友有帮助。万字长文,建议收藏后阅读。 一、概述 在AI的世界里,确保技术的行为符合我们的期望至关重要。OpenAI最近发布了一份名为Mo…...
微服务架构-正向治理与治理效果
目录 一、正向治理 1.1 概述 1.2 效率治理 1.2.1 概述 1.2.2 基于流量录制和回放的测试 1.2.3 基于仿真环境的测试 1.3 稳定性治理 1.3.1 概述 1.3.2 稳定性治理模型 1.3.3 基于容器化的稳定性治理 1.3.3.1 概述 1.3.3.2 测试 1.3.3.3 部署 1.3.3.3.1 概述 1.3.3…...

normalizing flows vs 直方图规定化
normalizing flows名字的由来 The base density P ( z ) P(z) P(z) is usually defined as a multivariate standard normal (i.e., with mean zero and identity covariance). Hence, the effect of each subsequent inverse layer is to gradually move or “flow” the da…...
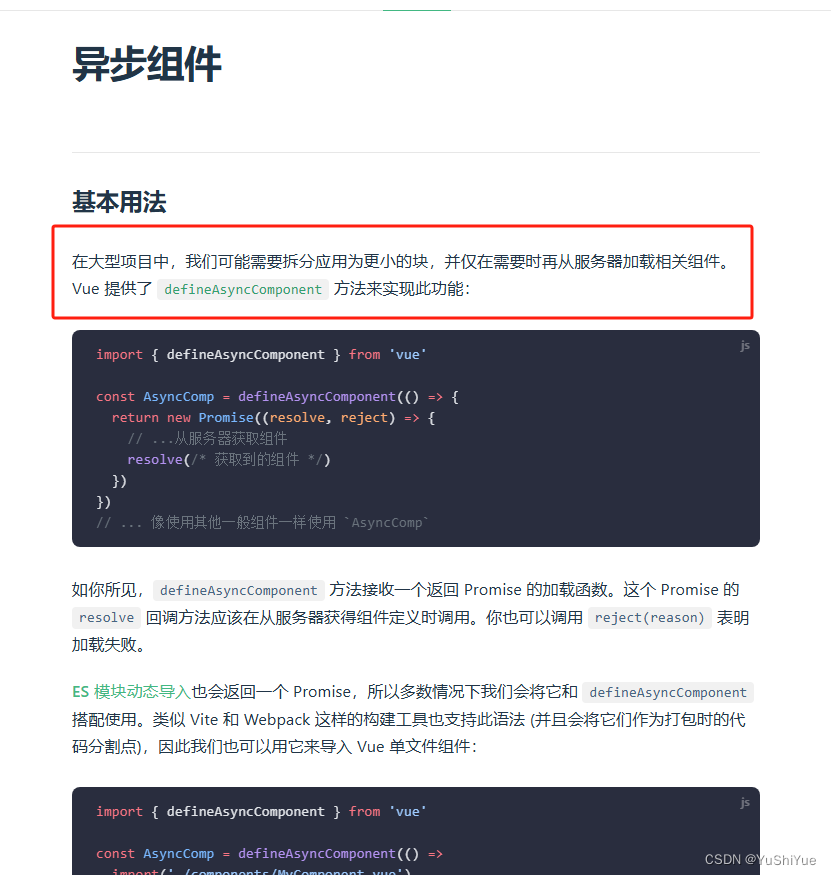
vite打包优化常用的技巧及思路
面试题:vitevue项目如何进行优化? 什么情况下会去做打包优化?一种是在搭建项目的时候就根据自己的经验把vite相关配置给处理好,另外一种是开发的过程中发现打包出来的静态资源越来越大,导致用户访问的时候资源加载慢&a…...

k8s学习--kubernetes服务自动伸缩之水平收缩(pod副本收缩)HPA详细解释与案例应用
文章目录 前言HPA简介简单理解详细解释HPA 的工作原理监控系统负载模式HPA 的优势使用 HPA 的注意事项应用类型 应用环境1.metircs-server部署2.HPA演示示例(1)部署一个服务(2)创建HPA对象(3)执行压测 前言…...

台式机ubuntu22.04安装nvidia驱动
总结一个极简易的安装方法 正常安装ubuntu 22.04正常更新软件 sudo apt update sudo apt upgrade -y参考ubuntu官方网站的说明https://ubuntu.com/server/docs/nvidia-drivers-installation#/ # 首先检查系统支持驱动的版本号 sudo ubuntu-drivers list我显示的内容如下&…...

C++ 11 【线程库】【包装器】
💓博主CSDN主页:麻辣韭菜💓 ⏩专栏分类:C修炼之路⏪ 🚚代码仓库:C高阶🚚 🌹关注我🫵带你学习更多C知识 🔝🔝 目录 前言 一、thread类的简单介绍 get_id…...

可视化数据科学平台在信贷领域应用系列四:决策树策略挖掘
信贷行业的风控策略挖掘是一个综合过程,需要综合考虑风控规则分析结果、效果评估、线上实时监测和业务管理需求等多个方面,以发现和制定有效的信贷风险管理策略。这些策略可能涉及贷款审批标准的调整、贷款利率的制定、贷款额度的设定等,在贷…...

数据查询深分页优化方案
大家好,我是冰河~~ 最近不少小伙伴在实际工作过程中,遇到了单表大数据量分页的问题,问我怎么优化分页查询。其实,这就是典型的深分页问题。今天趁着周末,给大家整理一些在深分页场景的简单处理方案。 一、普通分页查…...

Redis的主从复制
Redis主从复制是 Redis 内置的⼀种数据冗余和备份⽅式,同时也是分发读查询负载的⼀种⽅法。通过主从复制,可以有多个从服务器(Slave )复制⼀个主服务器(Master )的数据。在这个系统中,数据的复制…...

网络安全实战基础——实战工具与攻防环境介绍
一、实战集成工具 1. 虚拟机 VMware Workstation:大家熟知的虚拟机 Virtual Box:开源免费、轻量级 2. Kali Linux 工具集 信息收集 Nmap:免费开放的网络扫描和嗅探包,可探测主机是否在线,扫描主机端口和嗅探网络…...

vue2组件封装实战系列之tag组件
作为本系列的第一篇文章,不会过于的繁杂,并且前期的组件都会是比较简单的基础组件!但是不要忽视这些基础组件,因为纵观elementui、elementplus还是其他的流行组件库,组件库的封装都是套娃式的,很多复杂组件…...
(4):实用功能整理)
VBA实战(Excel)(4):实用功能整理
1.后台打开Excel 用于查数据,工作中要打开多个表获取数据再关闭的场景,利用此函数可以将excel表格作为后台数据库查询,快速实现客户要求,缺点是运行效率不够高。 Sub openexcel(exl_name As String)If Dir(addr, 16) Empty Then…...
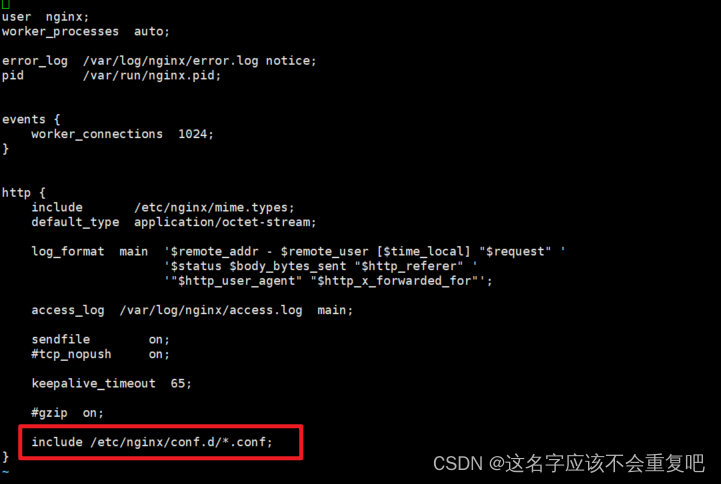
nginx mirror流量镜像详细介绍以及实战示例
nginx mirror流量镜像详细介绍以及实战示例 1.nginx mirror作用2.nginx安装3.修改配置3.1.nginx.conf3.2.conf.d目录下添加default.conf配置文件3.3.nginx配置注意事项3.3.nginx重启 4.测试 1.nginx mirror作用 为了便于排查问题,可能希望线上的请求能够同步到测试…...

Android14 WMS-窗口添加流程(二)-Server端
Android14 WMS-窗口添加流程(一)-Client端-CSDN博客 本文接着上文"Android14 WMS-窗口添加流程(一)-Client端"往下讲。也就是WindowManagerService#addWindow流程。 目录 一. WindowManagerService#addWindow 标志1:mPolicy.checkAddPermission 标志…...

【传知代码】DETR[端到端目标检测](论文复现)
前言:想象一下,当自动驾驶汽车行驶在繁忙的街道上,DETR能够实时识别出道路上的行人、车辆、交通标志等目标,并准确预测出它们的位置和轨迹。这对于提高自动驾驶的安全性、减少交通事故具有重要意义。同样,在安防监控、…...
Edge浏览器十大常见问题,一次性解决!
Edge曾被称为最好用的浏览器,拳打Chrome脚踢firefox, 可如今却隐藏着像是播放卡顿、下载缓慢、广告繁多等诸多问题,不知道各位还在用吗? 今天小编收集整理了Edge浏览器十大烦人问题,并提供简单有效的解决办法,让你的E…...

lubuntu / ubuntu 配置静态ip
一、查看原始网络配置信息 1、获取网卡名称 ifconfig 2、查询网关IP route -n 二、编辑配置文件 去/etc/netplan目录找到配置文件,配置文件名一般为01-network-manager-all.yaml sudo vim /etc/netplan/01-network-manager-all.yaml文件打开后内容如下 # This …...
15、matlab绘图汇总(图例、标题、坐标轴、线条格式、颜色和散点格式设置)
1、plot()函数默认格式画图 代码: x0:0.1:20;%绘图默认格式 ysin(x); plot(x,y) 2、X轴和Y轴显示范围/axis()函数 代码: x0:0.1:20;%绘图默认格式 ysin(x); plot(x,y) axis([0 21 -1.1 1.1])%设置范围 3、网格显示/grid on函数 代码: …...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
