深度学习 - 梯度下降优化方法
梯度下降的基本概念
梯度下降(Gradient Descent)是一种用于优化机器学习模型参数的算法,其目的是最小化损失函数,从而提高模型的预测精度。梯度下降的核心思想是通过迭代地调整参数,沿着损失函数下降的方向前进,最终找到最优解。
生活中的背景例子:寻找山谷的最低点
想象你站在一个山谷中,眼睛被蒙住,只能用脚感受地面的坡度来找到山谷的最低点(即损失函数的最小值)。你每一步都想朝着坡度下降最快的方向走,直到你感觉不到坡度,也就是你到了最低点。这就好比在优化一个模型时,通过不断调整参数,使得模型的预测误差(损失函数)越来越小,最终找到最佳参数组合。
梯度下降的具体方法及其优化
1. 批量梯度下降(Batch Gradient Descent)
生活中的例子:
你决定每次移动之前,都要先测量整个山谷的坡度,然后再决定移动的方向和步幅。虽然每一步的方向和步幅都很准确,但每次都要花很多时间来测量整个山谷的坡度。
公式:
θ : = θ − η ⋅ ∇ θ J ( θ ) \theta := \theta - \eta \cdot \nabla_{\theta} J(\theta) θ:=θ−η⋅∇θJ(θ)
其中:
- θ \theta θ是模型参数
- η \eta η是学习率
- ∇ θ J ( θ ) \nabla_{\theta} J(\theta) ∇θJ(θ)是损失函数 J ( θ ) J(\theta) J(θ)关于 θ \theta θ的梯度
API:
TensorFlow:
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)
PyTorch:
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
批量梯度下降过程图像python代码
import numpy as np
import matplotlib.pyplot as plt# 损失函数: y = x^2
def loss(x):return x ** 2# 损失函数的梯度: dy/dx = 2x
def gradient(x):return 2 * x# 批量梯度下降
def batch_gradient_descent(start, learning_rate, iterations):x = startpath = [x]for i in range(iterations):grad = gradient(x)x = x - learning_rate * gradpath.append(x)return path# 参数
start = 10
learning_rate = 0.1
iterations = 20# 运行梯度下降
path = batch_gradient_descent(start, learning_rate, iterations)# 绘制图像
x = np.linspace(-10, 10, 100)
y = loss(x)
plt.plot(x, y, label='Loss Function')
plt.scatter(path, [loss(p) for p in path], color='red', label='Batch Gradient Descent Path')
plt.xlabel('x')
plt.ylabel('Loss')
plt.legend()
plt.title('Batch Gradient Descent')
plt.show()
- 从图像可知,批量梯度下降每次使用整个训练集计算梯度并更新参数,适用于小规模数据集,收敛稳定,但计算开销大。
2. 随机梯度下降(Stochastic Gradient Descent, SGD)
生活中的例子:
你决定每一步都只根据当前所在位置的坡度来移动。虽然这样可以快速决定下一步怎么走,但由于只考虑当前点,可能会导致路径不稳定,有时候会走过头。
公式:
θ : = θ − η ⋅ ∇ θ J ( θ ; x ( i ) , y ( i ) ) \theta := \theta - \eta \cdot \nabla_{\theta} J(\theta; x^{(i)}, y^{(i)}) θ:=θ−η⋅∇θJ(θ;x(i),y(i))
其中 ( x ( i ) , y ( i ) ) (x^{(i)}, y^{(i)}) (x(i),y(i))是当前样本的数据
API:
TensorFlow 和 PyTorch 中的API与批量梯度下降相同,具体行为取决于数据的加载方式。例如在训练时可以一批数据包含一个样本。
随机梯度下降过程图像python代码
import numpy as np
import matplotlib.pyplot as plt# 损失函数: y = x^2
def loss(x):return x ** 2# 损失函数的梯度: dy/dx = 2x
def gradient(x):return 2 * x# 随机梯度下降
def stochastic_gradient_descent(start, learning_rate, iterations):x = startpath = [x]for i in range(iterations):grad = gradient(x)x = x - learning_rate * grad * np.random.uniform(0.5, 1.5) # 模拟随机样本的影响path.append(x)return path# 参数
start = 10
learning_rate = 0.1
iterations = 20# 运行梯度下降
path = stochastic_gradient_descent(start, learning_rate, iterations)# 绘制图像
x = np.linspace(-10, 10, 100)
y = loss(x)
plt.plot(x, y, label='Loss Function')
plt.scatter(path, [loss(p) for p in path], color='red', label='SGD Path')
plt.xlabel('x')
plt.ylabel('Loss')
plt.legend()
plt.title('Stochastic Gradient Descent')
plt.show()- 随机梯度下降每次使用一个样本计算梯度并更新参数,计算效率高,适用于大规模数据集,但收敛不稳定,容易出现抖动。
3. 小批量梯度下降(Mini-Batch Gradient Descent)
生活中的例子:
你决定每次移动之前,只测量周围一小部分区域的坡度,然后根据这小部分区域的平均坡度来决定方向和步幅。这样既不需要花太多时间测量整个山谷,也不会因为只看一个点而导致路径不稳定。
公式:
θ : = θ − η ⋅ ∇ θ J ( θ ; B ) \theta := \theta - \eta \cdot \nabla_{\theta} J(\theta; \mathcal{B}) θ:=θ−η⋅∇θJ(θ;B)
其中 B \mathcal{B} B是当前小批量的数据
API:
TensorFlow 和 PyTorch 中的API与批量梯度下降相同,但在数据加载时使用小批量。
小批量梯度下降过程图像python代码
import numpy as np
import matplotlib.pyplot as plt# 损失函数: y = x^2
def loss(x):return x ** 2# 损失函数的梯度: dy/dx = 2x
def gradient(x):return 2 * x# 小批量梯度下降
def mini_batch_gradient_descent(start, learning_rate, iterations, batch_size=5):x = startpath = [x]for i in range(iterations):grad = gradient(x)x = x - learning_rate * grad * np.random.uniform(0.8, 1.2) # 模拟小批量样本的影响path.append(x)return path# 参数
start = 10
learning_rate = 0.1
iterations = 20# 运行梯度下降
path = mini_batch_gradient_descent(start, learning_rate, iterations)# 绘制图像
x = np.linspace(-10, 10, 100)
y = loss(x)
plt.plot(x, y, label='Loss Function')
plt.scatter(path, [loss(p) for p in path], color='red', label='Mini-Batch Gradient Descent Path')
plt.xlabel('x')
plt.ylabel('Loss')
plt.legend()
plt.title('Mini-Batch Gradient Descent')
plt.show()
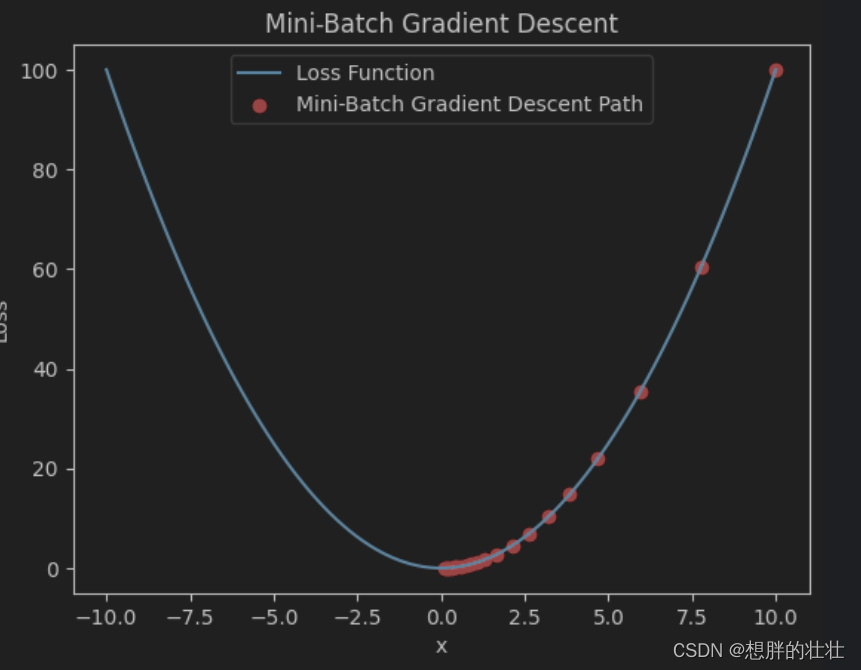
- 小批量梯度下降每次使用一个小批量样本计算梯度并更新参数,平衡了计算效率和稳定性。
4. 动量法(Momentum)
生活中的例子:
你在移动时,不仅考虑当前的坡度,还考虑之前几步的移动方向,就像带着惯性一样。如果前几步一直往一个方向走,那么你会倾向于继续往这个方向走,减少来回震荡。
公式:
v : = β v + ( 1 − β ) ∇ θ J ( θ ) v := \beta v + (1 - \beta) \nabla_{\theta} J(\theta) v:=βv+(1−β)∇θJ(θ)
θ : = θ − η v \theta := \theta - \eta v θ:=θ−ηv
其中:
- v v v是动量项
- β \beta β是动量系数(通常接近1,如0.9)
API:
TensorFlow:
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01, momentum=0.9)
PyTorch:
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
动量法图像python代码
import numpy as np
import matplotlib.pyplot as plt# 损失函数: y = x^2
def loss(x):return x ** 2# 损失函数的梯度: dy/dx = 2x
def gradient(x):return 2 * x# 动量法
def momentum_gradient_descent(start, learning_rate, iterations, beta=0.9):x = startv = 0path = [x]for i in range(iterations):grad = gradient(x)v = beta * v + (1 - beta) * gradx = x - learning_rate * vpath.append(x)return path# 参数
start = 10
learning_rate = 0.1
iterations = 20# 运行梯度下降
path = momentum_gradient_descent(start, learning_rate, iterations)# 绘制图像
x = np.linspace(-10, 10, 100)
y = loss(x)
plt.plot(x, y, label='Loss Function')
plt.scatter(path, [loss(p) for p in path], color='red', label='Momentum Path')
plt.xlabel('x')
plt.ylabel('Loss')
plt.legend()
plt.title('Momentum Gradient Descent')
plt.show()
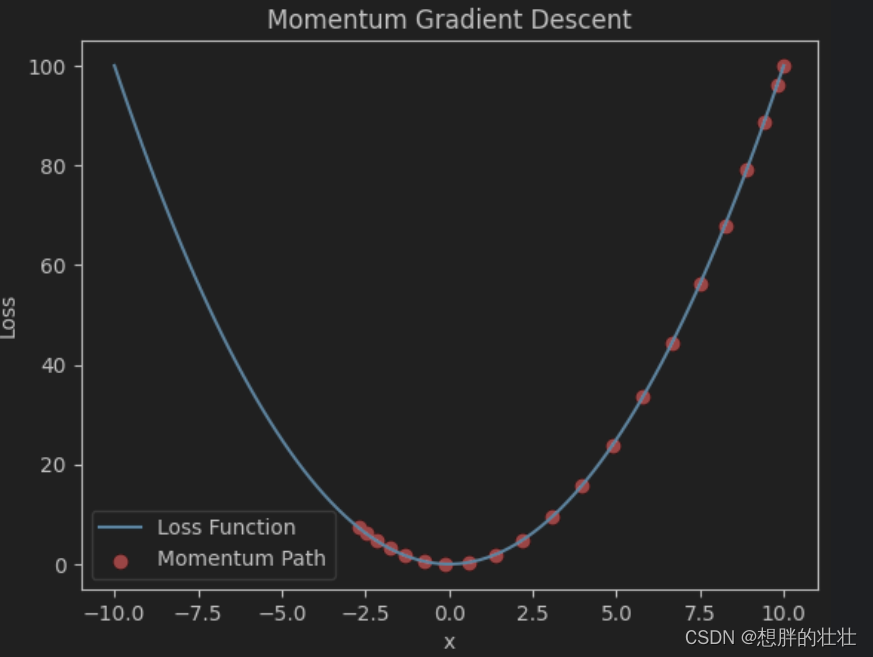
- 动量法通过引入动量项加速收敛并减少震荡,适用于深度神经网络训练。
5. RMSProp
生活中的例子:
你在移动时,会根据最近一段时间内每一步的坡度情况,动态调整步幅。比如,当坡度变化剧烈时,你会迈小步,当坡度变化平缓时,你会迈大步。
公式:
s : = β s + ( 1 − β ) ( ∇ θ J ( θ ) ) 2 s := \beta s + (1 - \beta) (\nabla_{\theta} J(\theta))^2 s:=βs+(1−β)(∇θJ(θ))2
θ : = θ − η s + ϵ ∇ θ J ( θ ) \theta := \theta - \frac{\eta}{\sqrt{s + \epsilon}} \nabla_{\theta} J(\theta) θ:=θ−s+ϵη∇θJ(θ)
其中:
- s s s是梯度平方的加权平均值
- ϵ \epsilon ϵ是一个小常数,防止除零错误
API:
TensorFlow:
optimizer = tf.keras.optimizers.RMSprop(learning_rate=0.001)
PyTorch:
optimizer = torch.optim.RMSprop(model.parameters(), lr=0.001)
RMSProp图像python代码
import numpy as np
import matplotlib.pyplot as plt# 损失函数: y = x^2
def loss(x):return x ** 2# 损失函数的梯度: dy/dx = 2x
def gradient(x):return 2 * x# RMSProp
def rmsprop_gradient_descent(start, learning_rate, iterations, beta=0.9, epsilon=1e-8):x = starts = 0path = [x]for i in range(iterations):grad = gradient(x)s = beta * s + (1 - beta) * grad**2x = x - learning_rate * grad / (np.sqrt(s) + epsilon)path.append(x)return path# 参数
start = 10
learning_rate = 0.1
iterations = 20# 运行梯度下降
path = rmsprop_gradient_descent(start, learning_rate, iterations)# 绘制图像
x = np.linspace(-10, 10, 100)
y = loss(x)
plt.plot(x, y, label='Loss Function')
plt.scatter(path, [loss(p) for p in path], color='red', label='RMSProp Path')
plt.xlabel('x')
plt.ylabel('Loss')
plt.legend()
plt.title('RMSProp Gradient Descent')
plt.show()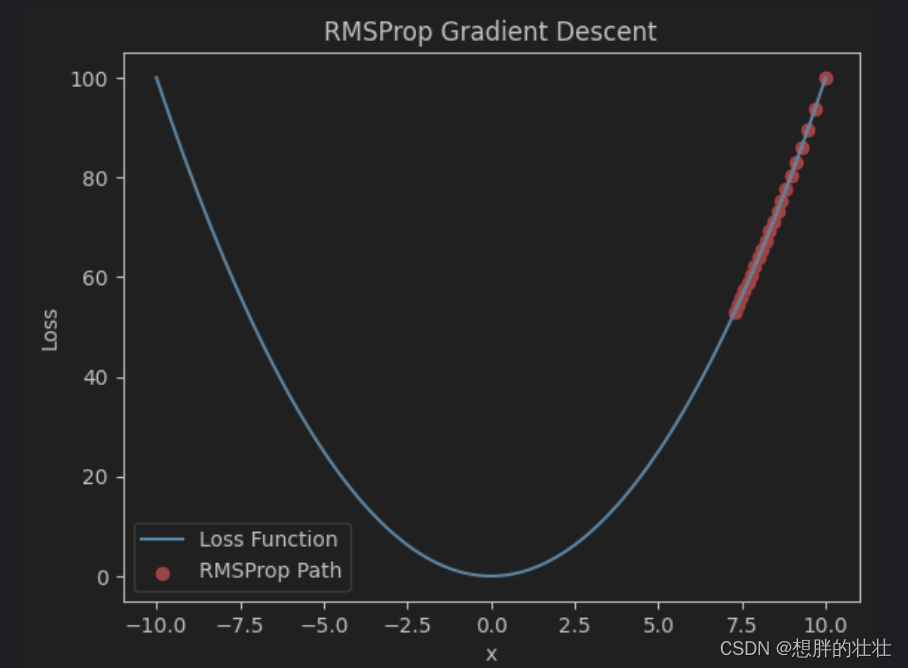
- RMSProp动态调整学习率,通过对梯度平方的加权平均值进行调整,适用于处理非平稳目标。
6. Adam(Adaptive Moment Estimation)
生活中的例子:
你在移动时,结合动量法和RMSProp的优点,不仅考虑之前的移动方向(动量),还根据最近一段时间内的坡度变化情况(调整步幅),从而使移动更加平稳和高效。
公式:
m : = β 1 m + ( 1 − β 1 ) ∇ θ J ( θ ) m := \beta_1 m + (1 - \beta_1) \nabla_{\theta} J(\theta) m:=β1m+(1−β1)∇θJ(θ)
v : = β 2 v + ( 1 − β 2 ) ( ∇ θ J ( θ ) ) 2 v := \beta_2 v + (1 - \beta_2) (\nabla_{\theta} J(\theta))^2 v:=β2v+(1−β2)(∇θJ(θ))2
m ^ : = m 1 − β 1 t \hat{m} := \frac{m}{1 - \beta_1^t} m^:=1−β1tm
v ^ : = v 1 − β 2 t \hat{v} := \frac{v}{1 - \beta_2^t} v^:=1−β2tv
θ : = θ − η m ^ v ^ + ϵ \theta := \theta - \eta \frac{\hat{m}}{\sqrt{\hat{v}} + \epsilon} θ:=θ−ηv^+ϵm^
其中:
- m m m和 v v v分别是梯度的一阶和二阶动量
- β 1 \beta_1 β1和 β 2 \beta_2 β2是动量系数(通常分别取0.9和0.999)
- m ^ \hat{m} m^和 v ^ \hat{v} v^是偏差校正后的动量项
- t t t是时间步
API:
TensorFlow:
optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)
PyTorch:
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
Adam图像python代码
import numpy as np
import matplotlib.pyplot as plt# 损失函数: y = x^2
def loss(x):return x ** 2# 损失函数的梯度: dy/dx = 2x
def gradient(x):return 2 * x# Adam
def adam_gradient_descent(start, learning_rate, iterations, beta1=0.9, beta2=0.999, epsilon=1e-8):x = startm = 0v = 0path = [x]for t in range(1, iterations + 1):grad = gradient(x)m = beta1 * m + (1 - beta1) * gradv = beta2 * v + (1 - beta2) * grad**2m_hat = m / (1 - beta1**t)v_hat = v / (1 - beta2**t)x = x - learning_rate * m_hat / (np.sqrt(v_hat) + epsilon)path.append(x)return path# 参数
start = 10
learning_rate = 0.1
iterations = 20# 运行梯度下降
path = adam_gradient_descent(start, learning_rate, iterations)# 绘制图像
x = np.linspace(-10, 10, 100)
y = loss(x)
plt.plot(x, y, label='Loss Function')
plt.scatter(path, [loss(p) for p in path], color='red', label='Adam Path')
plt.xlabel('x')
plt.ylabel('Loss')
plt.legend()
plt.title('Adam Gradient Descent')
plt.show()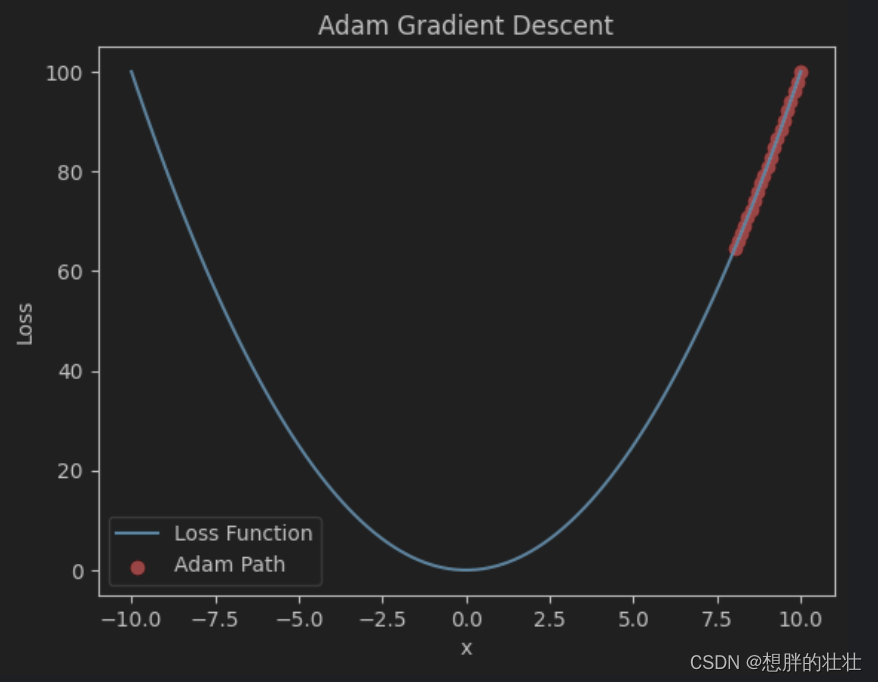
- Adam结合动量法和RMSProp的优点,自适应调整学习率,适用于各种优化问题。
综合应用示例
假设我们在使用TensorFlow和PyTorch训练一个简单的神经网络,以下是如何应用这些优化方法的示例代码。
TensorFlow 示例:
import tensorflow as tf# 定义模型
model = tf.keras.Sequential([tf.keras.layers.Dense(128, activation='relu', input_shape=(784,)),tf.keras.layers.Dense(10, activation='softmax')
])# 编译模型并选择优化器
optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)
model.compile(optimizer=optimizer, loss='sparse_categorical_crossentropy', metrics=['accuracy'])# 准备数据
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0# 训练模型
model.fit(x_train, y_train, epochs=10, batch_size=32)
PyTorch 示例:
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader# 定义模型
class SimpleNN(nn.Module):def __init__(self):super(SimpleNN, self).__init__()self.fc1 = nn.Linear(784, 128)self.fc2 = nn.Linear(128, 10)def forward(self, x):x = torch.relu(self.fc1(x))x = self.fc2(x)return xmodel = SimpleNN()# 选择优化器
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
criterion = nn.CrossEntropyLoss()# 准备数据
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5,), (0.5,))])
train_dataset = datasets.MNIST(root='./data', train=True, transform=transform, download=True)
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)# 训练模型
for epoch in range(10):for batch in train_loader:x_train, y_train = batchx_train = x_train.view(x_train.size(0), -1) # Flatten the imagesoptimizer.zero_grad()outputs = model(x_train)loss = criterion(outputs, y_train)loss.backward()optimizer.step()
综合对比
| 优化方法 | 优点 | 缺点 | 可能出现的问题 | 适用场景 |
|---|---|---|---|---|
| 批量梯度下降(Batch GD) | 收敛稳定,适用于小规模数据集 | 每次迭代计算开销大,速度慢 | 难以处理大规模数据,容易陷入局部最优 | 小规模数据集,适合精确收敛 |
| 随机梯度下降(SGD) | 计算效率高,适用于大规模数据集 | 路径不稳定,波动较大 | 收敛路径抖动大,不稳定 | 大规模数据集,在线学习,快速迭代 |
| 小批量梯度下降(Mini-Batch GD) | 平衡了计算效率和收敛稳定性 | 需要选择合适的小批量大小,计算量仍然较大 | 小批量大小选择不当可能影响收敛效果 | 大规模数据集,适合批量计算 |
| 动量法(Momentum) | 加速收敛,减少震荡 | 需要调整动量系数,增加了参数选择的复杂性 | 动量系数选择不当可能导致过冲 | 深度神经网络训练,加速收敛 |
| RMSProp | 动态调整学习率,适应非平稳目标 | 需要调整参数β和ε,参数选择复杂 | 参数选择不当可能影响收敛效果 | 非平稳目标,复杂优化问题 |
| Adam | 结合动量法和RMSProp优点,自适应调整学习率,收敛快 | 需要调整多个参数,计算复杂性高 | 参数选择不当可能影响收敛效果 | 各种优化问题,特别是深度学习模型训练 |
更多问题咨询
CosAI
相关文章:

深度学习 - 梯度下降优化方法
梯度下降的基本概念 梯度下降(Gradient Descent)是一种用于优化机器学习模型参数的算法,其目的是最小化损失函数,从而提高模型的预测精度。梯度下降的核心思想是通过迭代地调整参数,沿着损失函数下降的方向前进&#…...
Steam下载游戏很慢?一个设置解决!
博主今天重装系统后,用steam下载发现巨慢 500MB,都要下载半小时。 平时下载软件,一般1分钟就搞定了,于是大致就知道,设置应该出问题了 于是修改了,如下设置之后,速度翻了10倍。 如下&#x…...

51单片机采用定时器T1的方式1的中断计数方式,外接开关K4按4次后,8只LED闪烁不停
1、功能描述 采用定时器T1的方式1的中断计数方式,外接开关K4按4次后,8只LED闪烁不停 2、实验原理 定时器原理:8051的定时器可以用于计数外部事件或执行内部定时操作。在本程序中,定时器1被设置为模式2,即8位自动重装载定时器模式…...

windows系统 flutter 开发环境配置
1、管理员运行powershell,安装:Chocolatey 工具,粘贴复制运行下列脚本: Chocolatey 官方安装文档 Set-ExecutionPolicy Bypass -Scope Process -Force; [System.Net.ServicePointManager]::SecurityProtocol [System.Net.ServicePointManage…...
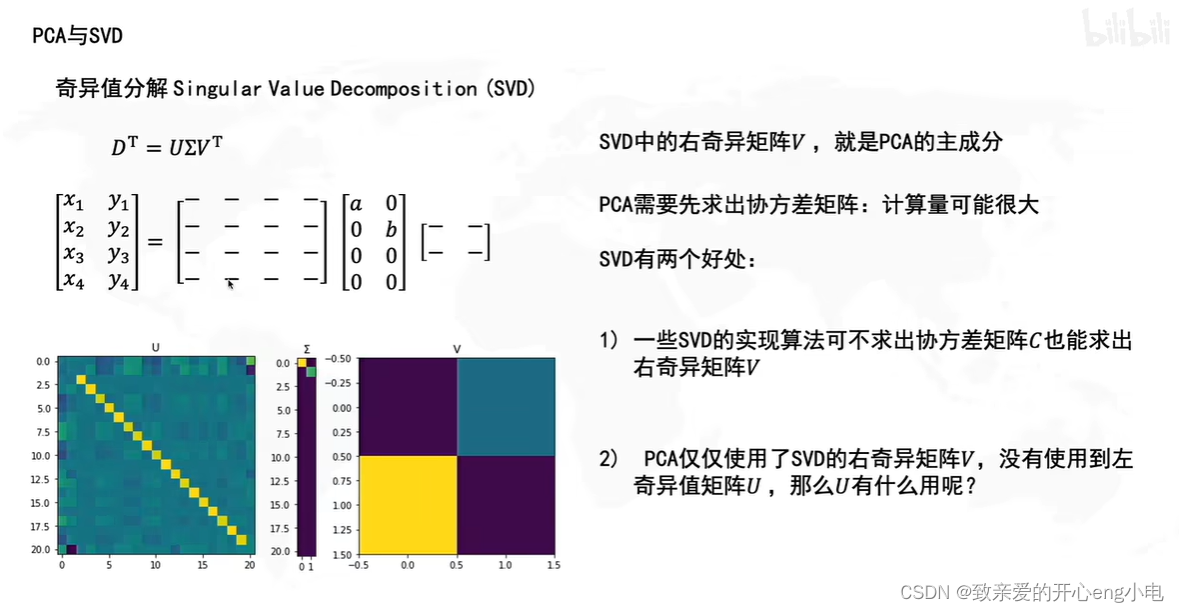
【线性代数】SVDPCA
用最直观的方式告诉你:什么是主成分分析PCA_哔哩哔哩_bilibili 奇异值分解singular value decomposition,SVD principal component analysis,PCA 降维操作 pca就是降维后使得信息损失最小 投影在坐标轴上的点越分散,信息保留越多 pca的实现…...

1.Vue2使用ElementUI-初识及环境搭建
目录 1.下载nodejs v16.x 2.设置淘宝镜像源 3.安装脚手架 4.创建一个项目 5.项目修改 代码地址:source-code: 源码笔记 1.下载nodejs v16.x 下载地址:Node.js — Download Node.js 2.设置淘宝镜像源 npm config set registry https://registry.…...
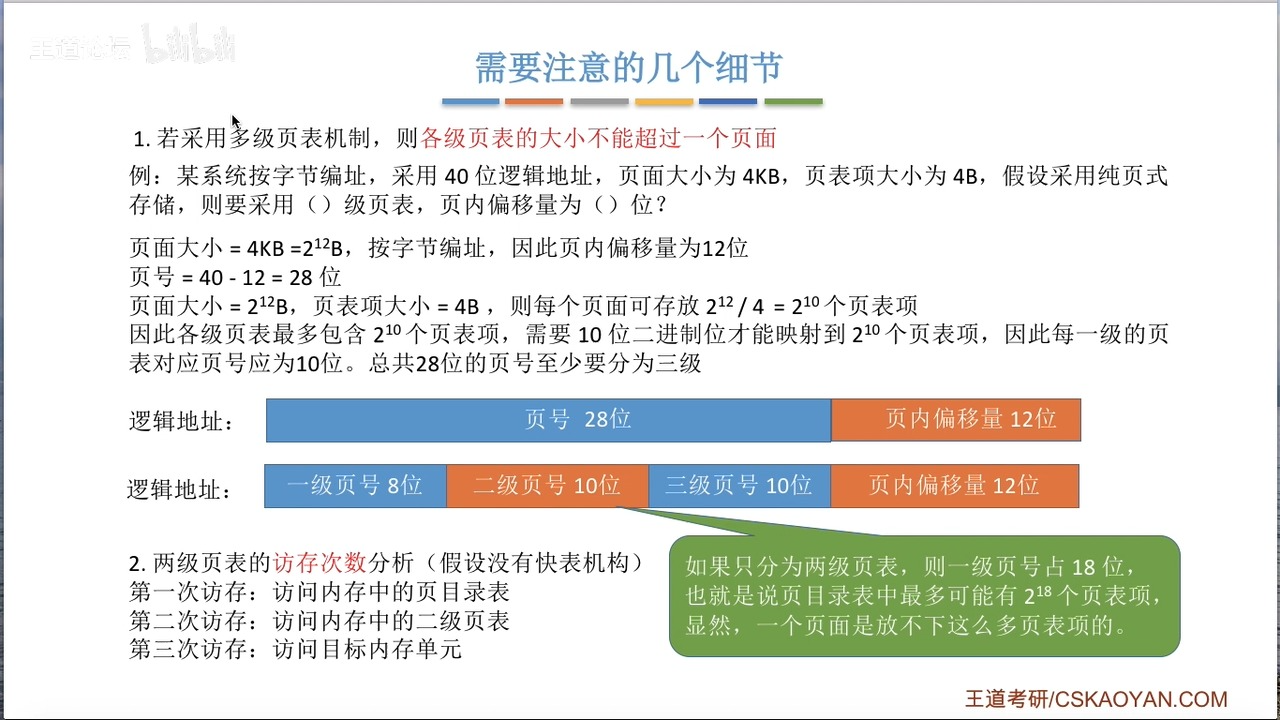
OS复习笔记ch7-3
承接上文我们讲完了页式管理和段式管理,接下来让我们深入讲解一下快表和二级页表 快表 快表和计算机组成原理讲的Cache原理如出一辙。为了减少访存的次数,OS在访问页面的时候创建了快表(Translation Lookaside Buffer ,简称TLB&…...
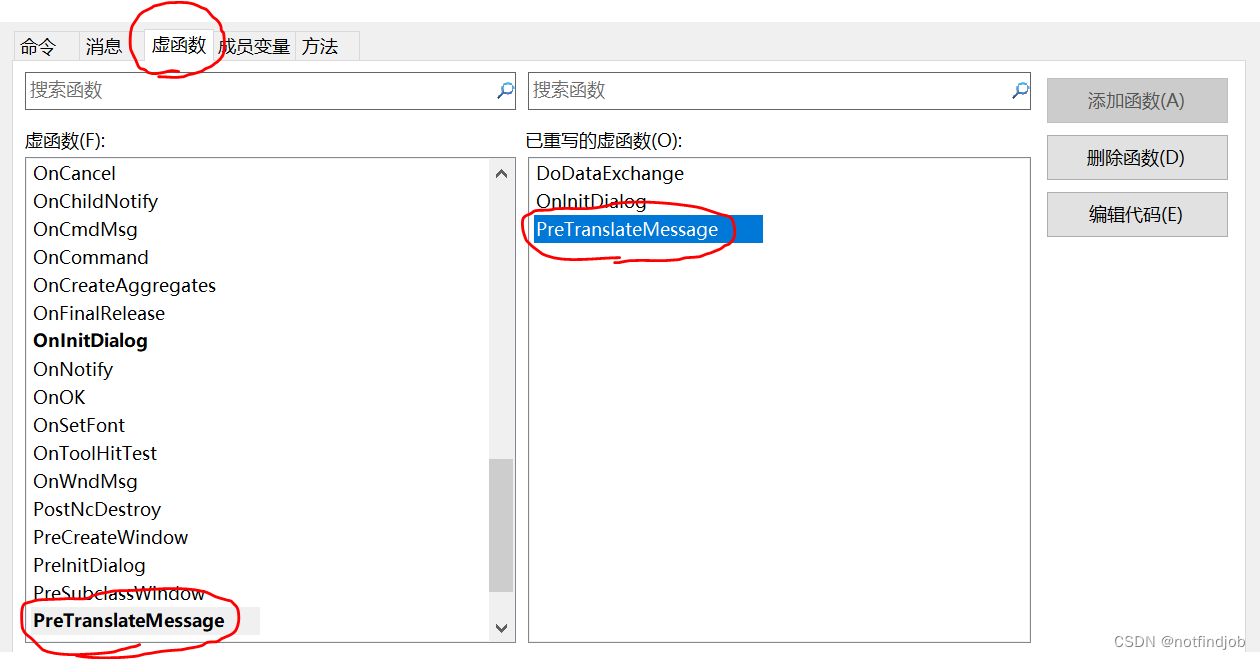
MFC 教程-回车时窗口退出问题
【问题描述】 MFC窗口默认时,按回车窗口会退出 【原因分析】 默认调用OnOK() 【解决办法】 重写虚函PreTranslateMessage BOOL CTESTMFCDlg::PreTranslateMessage(MSG* pMsg) {// TODO: 在此添加专用代码和/或调用基类// 修改回车键的操作反应 if (pMsg->…...
CTFHUB-SQL注入-字符型注入
目录 查询数据库名 查询数据库中的表名 查询表中数据 总结 此题目和上一题相似,一个是整数型注入,一个是字符型注入。字符型注入就是注入字符串参数,判断回显是否存在注入漏洞。因为上一题使用手工注入查看题目 flag ,这里就不…...

Docker配置Redis集群以及主从扩容与缩容
基础镜像拉取 docker run -p 6379:6379 -d redis:6.0.8 配置文件以及数据卷挂载 # 开启密码验证(可选) requirepass 1234 # 允许redis外地连接,需要注释掉绑定的IP # bind 127.0.0.1 # 关闭保护模式(可选) protected-m…...

【计算机网络】 传输层
一、传输层提供的服务 1.1 传输层的功能 1.1.1 传输层的功能如下: 传输层提供应用进程之间的逻辑通信(即端到端的通信)。与网络层的区别是:网络层提供的是主机之间的逻辑通信。 1.1.2 复用和分用 传输层要还要对收到的报文进行…...

山东大学软件学院项目实训-创新实训-基于大模型的旅游平台(二十七)- 微服务(7)
11.1 : 同步调用的问题 11.2 异步通讯的优缺点 11.3 MQ MQ就是事件驱动架构中的Broker 安装MQ docker run \-e RABBITMQ_DEFAULT_USERxxxx \-e RABBITMQ_DEFAULT_PASSxxxxx \--name mq \--hostname mq1 \-p 15672:15672 \-p 5672:5672 \-d \rabbitmq:3-management 浏览器访问1…...

Java Web应用,IPv6问题解决
在Java Web程序中,如果使用Tomcat并遇到了IPv6相关的问题,可以通过以下几种方式来解决: 1. 配置Tomcat以使用IPv4 默认情况下,Java可能会优先使用IPv6。如果你希望Tomcat使用IPv4,最简单的方法是通过设置系统属性来强…...
MyBatis二级缓存开启条件
MyBatis缓存为俩层体系。分为一级缓存和二级缓存。 一级缓存: 一级缓存默认开启,一级缓存的作用域是SqlSession级别的,这意味着当你更换SqlSession之后就不能再利用原来的SqlSession的一级缓存了。不同的SqlSession之间的一级缓存是隔离的。…...

golang 不用sleep如何实现实现每隔指定时间执行一次for循环?
今天介绍的是在go语言里面不用time.Sleep, 使用for range 定时器管道 来实现按照我们指定的时间间隔来执行for循环, 即: for range ticker.C { } 这样就实现了for每隔指定时间执行一次,除非管道被关闭,否则for而且会一直柱塞当前线…...

【el-tooltips改造】Vue实现文本溢出才显示el-tooltip,否则不显示el-tooltips
实现原理: 使用disabled属性控制el-tooltip的content显示与隐藏; 目标: 1行省略、多行省略、可缩放页面内的文本省略都有效。 实现方式: 1、自定义全局指令,tooltipAutoShow.js代码如下(参考的el-table中的…...
【Python数据类型的奥秘】:构建程序基石,驾驭信息之海
文章目录 🚀Python数据类型🌈1. 基本概念⭐2. 转化👊3. 数值运算💥4. 数值运算扩展(math库常用函数) 🚀Python数据类型 🌈1. 基本概念 整数(int):整数是没有小数部分的数…...

vue使用html2canvas截图下载时,存在svg或者img或者特殊字体时截图不全的解决办法
使用html2canvas进行div截图时,存在svg和img的解决办法 写在前面:vue使用html2canvas截图时,存在svg或者img或者特殊字体时截图时空白,或者不全解决办法如下第一步,svg或者img先转base64(如果是特殊字体&am…...

机器学习----奥卡姆剃刀定律
奥卡姆剃刀定律(Occam’s Razor)是一条哲学原则,通常表述为“如无必要,勿增实体”(Entities should not be multiplied beyond necessity)或“在其他条件相同的情况下,最简单的解释往往是最好的…...

【设计模式】行为型设计模式之 模板方法模式
介绍 GOF 定义 模板方法模式 Template Method Design Pattern :模板方法模式在一个方法中定义一个算法骨架,并将某些步骤推迟到子类中去实现;模板方法在不改变算法整体结构的情况下,可以重新定义算法中的某些步骤。 代码举例 …...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...
