千益畅行,共享旅游卡,灵活同行,畅游无忧的全方位解析
千益畅行,共享旅游卡,满足您多样化的同行出行需求
近期,关于千益畅行共享旅游卡的咨询热度不减,尤其是关于其同行人数的限制问题。为了给大家一个清晰的解答,我们深入探讨了该旅游卡的特点和优势。
千益畅行共享旅游卡在同行人数方面展现了极高的灵活性。与传统的共享旅游卡相比,它不仅仅局限于2人同行,更能轻松满足2至6人的同行需求,甚至适应更大规模的多人出行。
该旅游卡的服务模式丰富多样,包括散拼团、纯玩团和企业团三种,每种模式都针对同行人数有不同的规定和优势。
在散拼团模式下,千益畅行共享旅游卡为游客提供了一系列免费服务,如接送机、全程酒店安排、团餐、大巴、导游、全程首道门票和旅游责任险等,无需额外支付任何费用。这些贴心的服务不仅让您的旅程更加便捷,还能为您节省数千元的团费。但请注意,散拼团的免费服务不包括往返目的地的交通费用、酒店内的自费项目以及景区内的自费项目。此外,若因个人原因造成未参团酒店、车位损失或中途离团,这些损失也不在免费服务范围内。不过,散拼团依然支持2至6人同行,为您的出行提供了更多便利。
对于追求更高自由度和个性化体验的游客,纯玩团模式将是您的理想选择。使用千益畅行共享旅游卡预约纯玩团时,您需要根据所选线路支付相应的费用。纯玩团在人数上没有限制,您可以根据自己的需求进行预约。除了支付正常的团费外,纯玩团中的自费项目需要您自己承担。与散拼团相同,若因个人原因造成未参团酒店、车位损失或中途离团,这些损失也不在免费服务范围内。
对于企业客户而言,千益畅行共享旅游卡同样提供了优质的服务。企业客户需要根据具体需求支付费用,一般为每人300元。一张旅游卡可以支持整个企业的出行需求,最高可达10000人。企业客户的需求可能包括舞台、会场、灯光、表演场地以及团队拓展场地等,费用会根据不同的需求条件有所变化。请注意,大型企业团并非所有线路都适用,有指定的旅游线路可供选择。您可以在千益畅行相关平台查询更多详细信息。
总的来说,千益畅行共享旅游卡在同行人数上提供了极大的灵活性,无论是散拼团、纯玩团还是企业团,都能满足您的出行需求。请根据您的实际需求选择合适的模式,让您的旅行更加省心、省钱、省力。
相关文章:

千益畅行,共享旅游卡,灵活同行,畅游无忧的全方位解析
千益畅行,共享旅游卡,满足您多样化的同行出行需求 近期,关于千益畅行共享旅游卡的咨询热度不减,尤其是关于其同行人数的限制问题。为了给大家一个清晰的解答,我们深入探讨了该旅游卡的特点和优势。 千益畅行共享旅游…...
Web IDE 在线编辑器综合实践(Web IDE 技术探索 三)
前言 前面两篇文章,我们简单讲述了 WebContainer/api 、Terminal 的基本使用,离完备的在线代码编辑器就差一个代码编辑了。今天通过 monaco editor ,来实现初级代码编辑功能,讲述的是整个应用的搭建,并不单独针对monac…...

Less is more VS 精一 [生活感悟]
"Less is More”和王阳明的“精一”思想确实有相似之处。 王阳明的“精一”思想强调的是专注于一件事,将其做到极致,这与"Less is More”中提倡的通过减少数量来提高质量的理念不谋而合。两者都强调了专注和深度的重要性,而不是追…...

函数的概念及图像
注: 判断两函数是否相同,只看定义域和对应法则。 1. 函数的定义 一般的,在一个变化过程中有两个变量 x,y。如果对于x在某个变化范围内的每一个确定值,按照某个对应法则,都有唯一确定的值y和他对应。那么y就…...
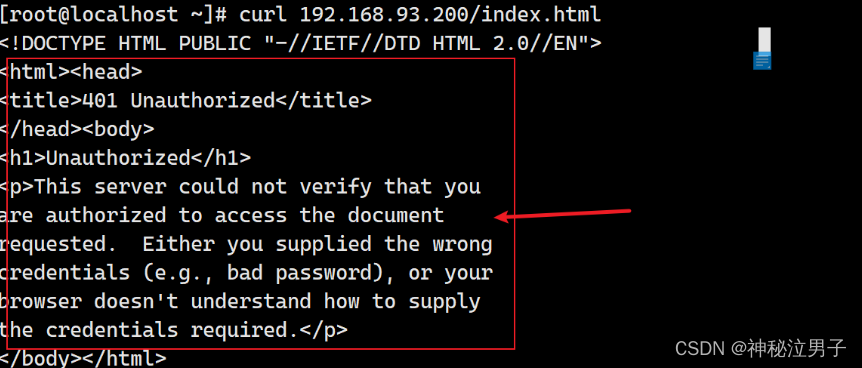
Linux中Apache网站基于Http服务的访问限制(基于地址/用户)
🏡作者主页:点击! 👨💻Linux高级管理专栏:点击! ⏰️创作时间:2024年6月3日11点44分 🀄️文章质量:95分 为了更好地控制对网站资源的访问,可…...

滚动条详解:跨平台iOS、Android、小程序滚动条隐藏及自定义样式综合指南
滚动条是用户界面中的图形化组件,用于指示和控制内容区域的可滚动范围。当元素内容超出其视窗边界时,滚动条提供可视化线索,并允许用户通过鼠标滚轮、触屏滑动或直接拖动滑块来浏览未显示部分,实现内容的上下或左右滚动。它在保持…...
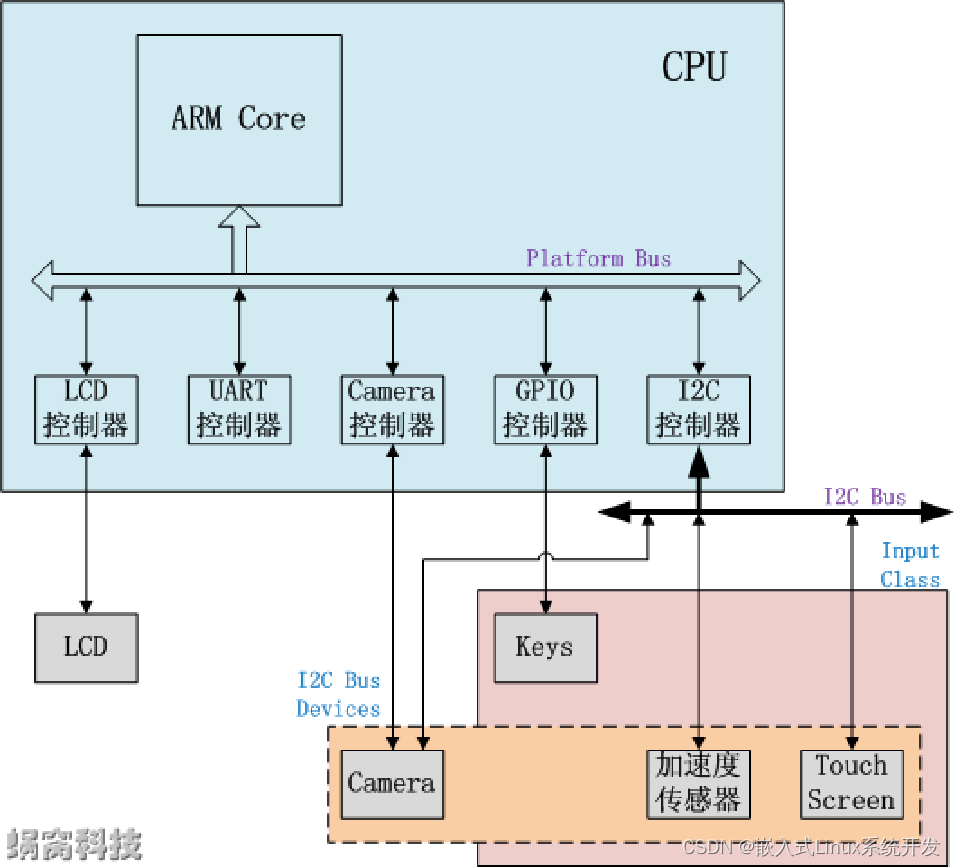
06 Linux 设备驱动模型
1、Overview Linux-2.6 引入的新的设备管理机制 - kobject 降低设备多样性带来的 Linux 驱动开发的复杂度,以及设备热拔插处理、电源管理等将硬件设备归纳、分类,然后抽象出一套标准的数据结构和接口驱动的开发,就简化为对内核所规定的数据结构的填充和实现驱动模型是 Linu…...
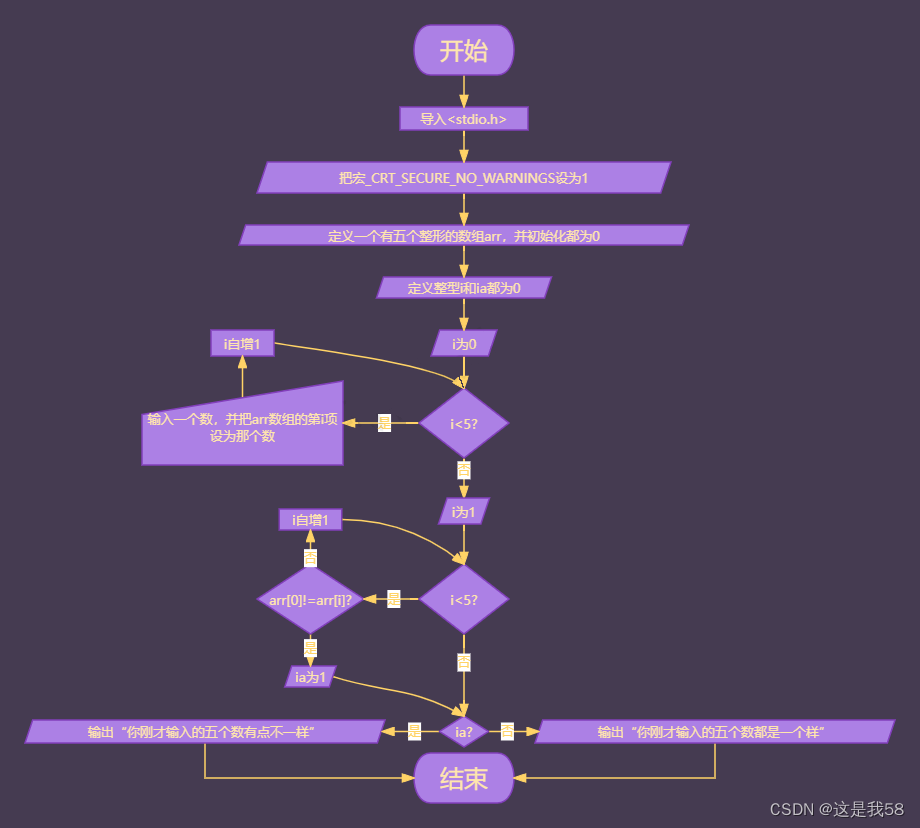
检测五个数是否一样的算法
目录 算法算法的输出与打印效果输出输入1输入2 打印打印1打印2 算法的流程图总结 算法 int main() {int arr[5] { 0 };int i 0;int ia 0;for (i 0; i < 5; i) { scanf("%d", &arr[i]); }for (i 1; i < 5; i) {if (arr[0] ! arr[i]) {ia 1;break;} }…...
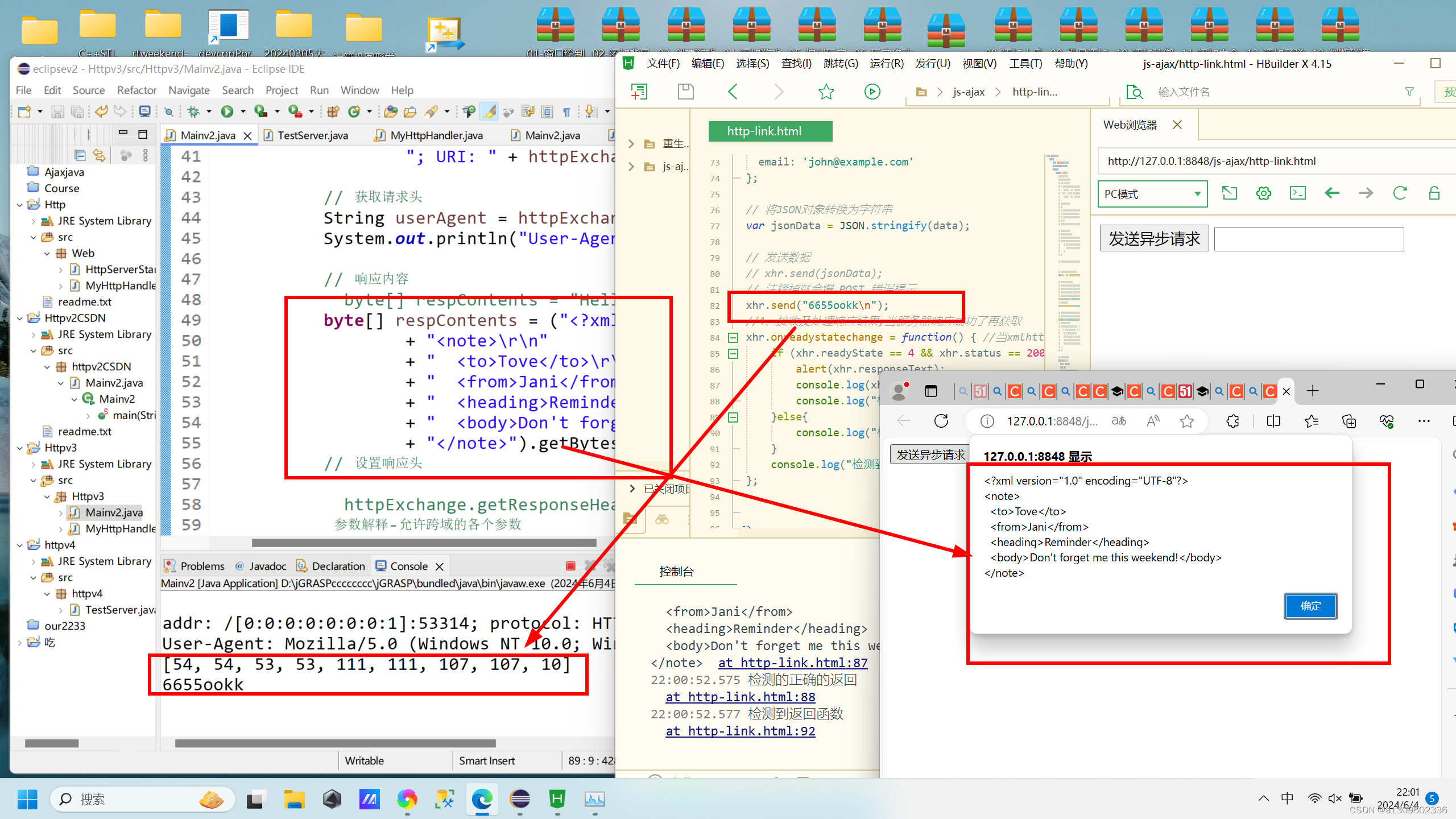
java 原生http服务器 测试JS前端ajax访问实现跨域传post数据
后端 java eclipse 字节流转字符 package Httpv3;import com.sun.net.httpserver.Headers; import com.sun.net.httpserver.HttpExchange; import com.sun.net.httpserver.HttpHandler; import com.sun.net.httpserver.HttpServer;import java.io.IOException; import java.i…...
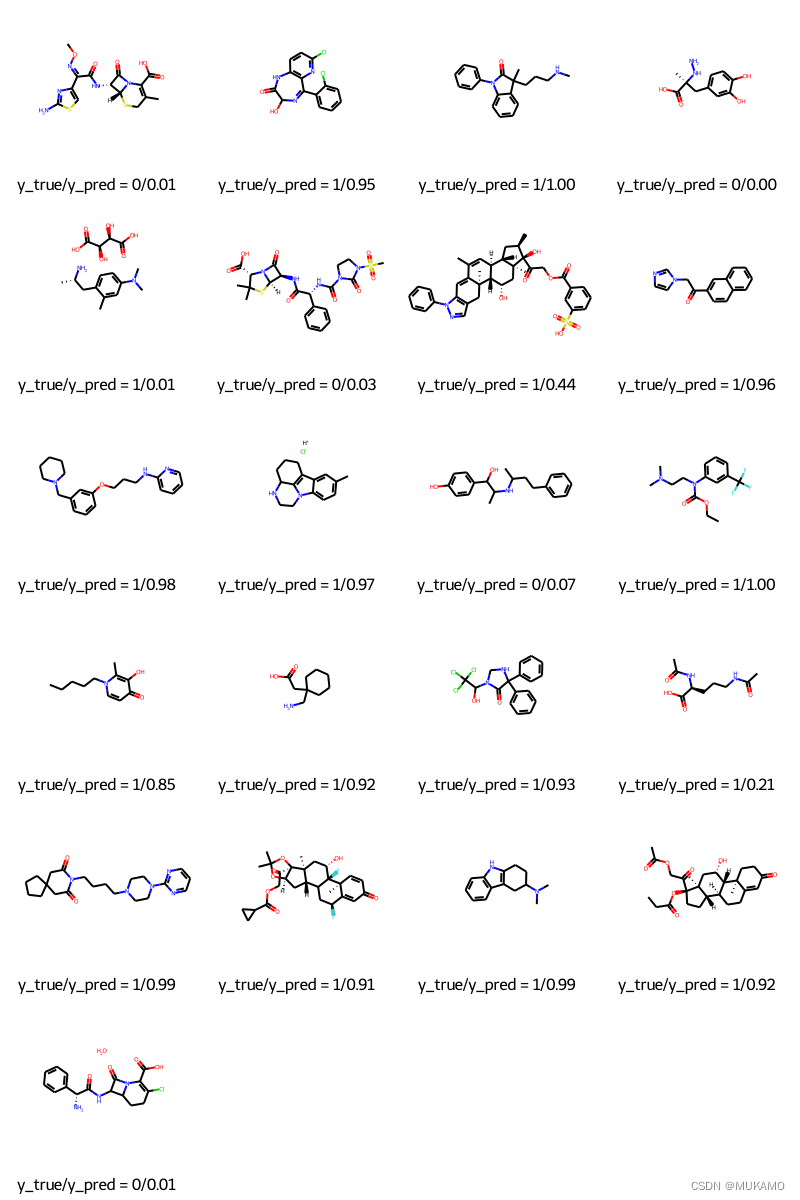
【机器学习】消息传递神经网络(MPNN)在分子预测领域的医学应用
1. 引言 1.1. 分子性质预测概述 分子性质预测是计算机辅助药物发现流程中至关重要的任务之一,它在许多下游应用如药物筛选和药物设计中发挥着核心作用: 1.1.1. 目的与重要性: 分子性质预测旨在通过分子内部信息(如原子坐标、原…...
Python Flask实现蓝图Blueprint配置和模块渲染
Python基础学习: Pyhton 语法基础Python 变量Python控制流Python 函数与类Python Exception处理Python 文件操作Python 日期与时间Python Socket的使用Python 模块Python 魔法方法与属性 Flask基础学习: Python中如何选择Web开发框架?Pyth…...

Vue10-事件修饰符
一、示例:<a>标签不执行默认的跳转行为 1-1、方式一 <a href"http://www.baidu.com" onclick"event.preventDefault();">点击我</a> 1-2、方式二 1-3、方式三:事件修饰符 二、Vue的六种事件修饰符 2-1、prevent&…...

oracle中如何查询特定日期?
1. select last_day(to_date(20230101,YYYYMMDD)) from dual; select last_day(to_date(V_END_DATE,YYYYMMDD)) from dual; --查询任意一天 当月的最后一天 2. select to_char(to_date(20230101,YYYYMMDD)-1,YYYYMMDD) INTO V_START_DATE FROM DUAL; select to_char(to_dat…...

Python使用rosbag使用getattr只能获取一层的数据,不能直接获取多层数据例如 a.b.c.d。使用for range写一个递归用来获取多层数据
使用for循环和range来遍历属性列表确实是一个更简单直观的方式,特别是不需要考虑性能优化和异常处理时。以下是使用for循环代替递归的示例代码: python def get_nested_attr(obj, attr_str): attrs attr_str.split(.) for attr in attrs: # 尝试获取下…...

LNWT--篇章三小测
问题1: BERT训练时候的学习率learning rate如何设置? 在训练初期使用较小的学习率(从 0 开始),在一定步数(比如 1000 步)内逐渐提高到正常大小(比如上面的 2e-5),避免模型过早进入…...

【NoSQL】Redis练习
1、redis的编译安装 systemctl stop firewalld systemctl disable firewalld setenforce 0 yum install -y gcc gcc-c make wget cd /opt wget https://download.redis.io/releases/redis-5.0.7.tar.gz tar zxvf redis-5.0.7.tar.gz -C /opt/cd /opt/redis-5.0.7/ # 编译 make…...

Git 和 Github 的使用
补充内容:EasyHPC - Git入门教程【笔记】 文章目录 常用命令配置信息分支管理管理仓库 概念理解SSH 密钥HTTPS 和 SSH 的区别在本地生成 SSH key在 Github 上添加 SSH key 使用的例子同步本地仓库的修改到远程仓库拉取远程仓库的修改到本地仓库拉取远程仓库的分支并…...

学习分享-断路器Hystrix与Sentinel的区别
断路器(Circuit Breaker)简介 断路器(Circuit Breaker)是一种用于保护分布式系统的服务稳定性和容错性的设计模式。它的主要作用是在检测到某个服务的调用出现故障(如超时、异常等)时,快速失败…...
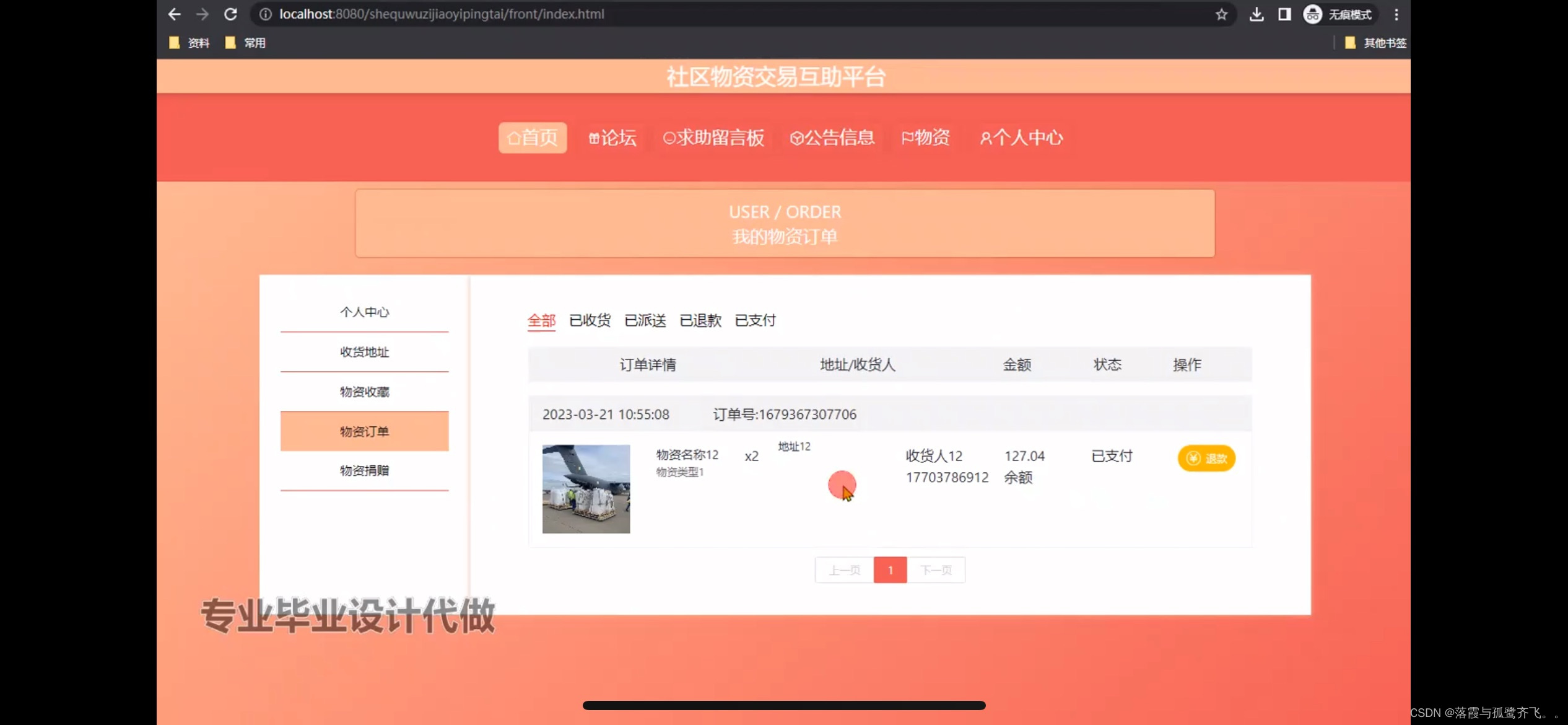
社区物资交易互助平台的设计
管理员账户功能包括:系统首页,个人中心,管理员管理,基础数据管理,论坛管理,公告信息管理 前台账户功能包括:系统首页,个人中心,论坛,求助留言板,公…...

19-Nacos-服务实例的权重设置
19-Nacos-服务实例的权重设置 1.根据权重负载均衡: 1.服务器设备性能有差异,部分实例所在及其性能较高,有一些较差,我们希望性能好的机器承担更多的用户请求 Nacos提供了权重配置来控制访问频率,权重越大则访问频率…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...
