当前位置： 首页 > news >正文

正大国际期货：什么是主力合约？

news 2026/2/8 23:32:50

一个期货品种，在同一时间段，会上市多个月份的合约， 由于主力合约交易量大，流动性高，一般建议新手交易主力合约。

 

主力合约通常指交易集中，流动性好的合约 ，即在一段时间内交易量和持仓量最大的一个合约。成熟期货市场的主力合约，一般是逐月轮换的，因此所有合约都有成为主力合约的机会。

我国现阶段，大部分品种形成了以1月、5月、9月份为主力合约的非连续性市场结构，未来当我国的期货市场参与者不断增多，可促进合约的流动性，可以给投资者移仓换月提供更多的选择。

交易主力合约，并不是交易者唯一的选择，但是主力合约流动性非常高，适合新手持有，远期合约开平仓时因缺少交易对手， 不易成交，所以建议投资者尽量减少持有远期不活跃合约！请知悉哦！

相关文章：

正大国际期货：什么是主力合约？

一个期货品种，在同一时间段，会上市多个月份的合约， 由于主力合约交易量大，流动性高，一般建议新手交易主力合约。 主力合约通常指交易集中，流动性好的合约 ，即在一段时间内交易量和持仓量最大的…...

编程日记 2024/6/9 15:26:41

codeforces round 949 div2

A Turtle and Piggy Are Playing a Game 题目&#xff1a; 思路&#xff1a;输出2的幂次b使得2^b为最大的不超过x的数 代码&#xff1a; #include <iostream>using namespace std;const int N 2e5 10;void solve() {int l, r;cin >> l >> r;if(r % 2) …...

编程日记 2024/6/9 15:24:37

分享美好，高清无阻 - 直播极简联网解决方案

1、需求背景 随着移动互联网、UGC模式和直播平台的发展&#xff0c;网络直播的门槛日益降低&#xff0c;越来越多的人希望成为直播的主角。基于物联网的户外直播无线联网解决方案应运而生&#xff0c;满足直播者的需求。 户外直播无线联网解决方案提供了无处不在的直播体验&a…...

编程日记 2024/6/9 15:22:35

贪心算法-加油站

一、题目描述 二、解题思路 1.运动过程分析 这里需要一个油箱剩余油量的变量resGas&#xff0c;初始化resGas0&#xff1b;还需要一个标记从什么位置当做初始位置的startIdx&#xff0c;初始化startIdx0。 我们从数组下标idx0处开始向后遍历&#xff0c;初始时startIdx0&#…...

编程日记 2024/6/9 15:21:34

【ArcGIS微课1000例】0116：将度-分-秒值转换为十进制度值（字段计算器VBA）

相关阅读：【ArcGIS微课1000例】0087：经纬度格式转换（度分秒转度、度转度分秒） 文章目录 一、计算方法二、计算案例一、计算方法 将度分秒转换为十进制度的简单等式： DD = (Seconds/3600) + (Minutes/60) + Degrees如果角度值是负数，则转换方法不同。其中一种方法是： …...

编程日记 2024/6/9 15:19:32

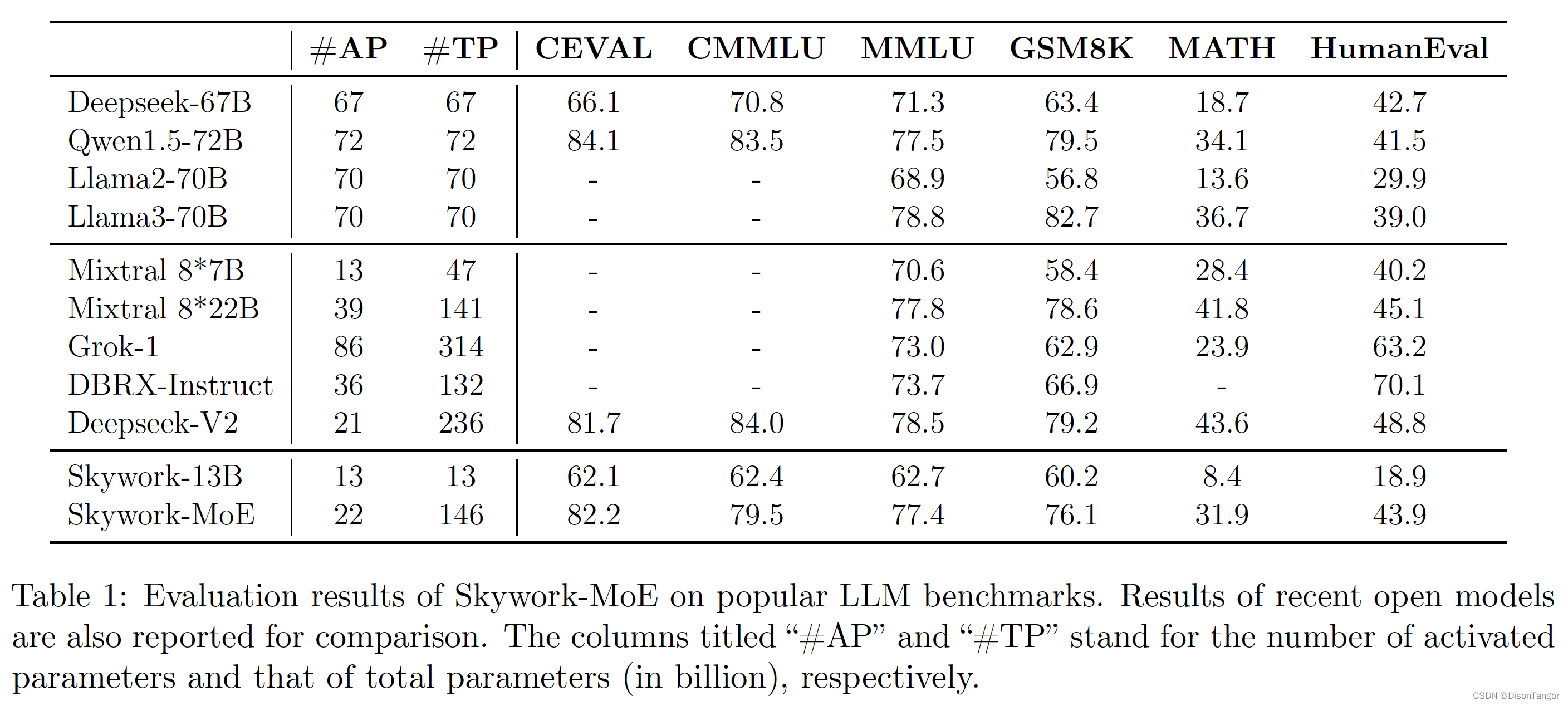
【中国开源生态再添一员】天工AI开源自家的Skywork

刚刚看到《AI高考作文出圈&#xff0c;网友票选天工AI居首》&#xff0c;没想到在Huggingface中发现了Skywork大模型。天工大模型由昆仑万维自研&#xff0c;是国内首个对标ChatGPT的双千亿级大语言模型&#xff0c;天工大模型通过自然语言与用户进行问答式交互&#xff0c;AI生…...

编程日记 2024/6/9 15:18:30

【机器学习300问】109、什么是岭回归模型？

在进行回归任务时间&#xff0c;可以能会遇到特征数量多于观测数量或某些特征变量之间相关性较高&#xff08;几乎线性相关&#xff09;时&#xff0c;标准的线性回归模型的系数估计可能非常不精确&#xff0c;可以理解成独立方程个数小于未知数个数此时方程有无穷多解。 例如&…...

编程日记 2024/6/9 15:16:29

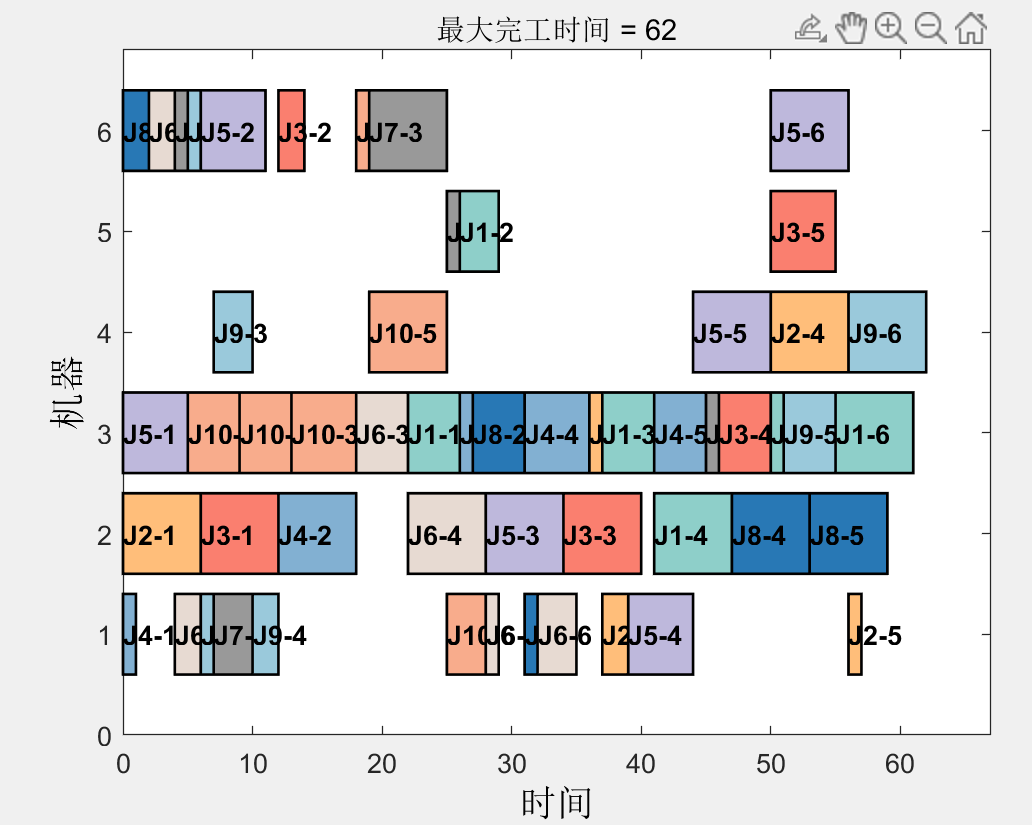
FJSP：烟花算法（FWA）求解柔性作业车间调度问题（FJSP），提供MATLAB代码

一、烟花算法介绍 参考文献&#xff1a; Tan, Y. and Y. Zhu. Fireworks Algorithm for Optimization. in Advances in Swarm Intelligence. 2010. Berlin, Heidelberg: Springer Berlin Heidelberg. 二、烟花算法求解FJSP 2.1FJSP模型介绍 柔性作业车间调度问题(Flexible …...

编程日记 2024/6/9 15:14:26

C++11 列表初始化(initializer_list)，pair

1. {} 初始化 C98 中&#xff0c;允许使用 {} 对数组进行初始化。 int arr[3] { 0, 1, 2 };C11 扩大了 {} 初始化 的使用范围&#xff0c;使其可用于所有内置类型和自定义类型。 struct Date {int _year;int _month;int _day;Date(int year, int month, int day):_year(year…...

编程日记 2024/6/9 15:10:23

Python3 笔记：字符串的 startswith() 和 endswith()

1、startswith() 方法用于检查字符串是否是以指定子字符串开头&#xff0c;如果是则返回 True&#xff0c;否则返回 False。如果参数 beg 和 end 指定了值&#xff0c;则在指定范围内检查。 语法&#xff1a;str.startswith(substr, beg0,endlen(string)) 参数&#xff1a; s…...

编程日记 2024/6/9 15:09:22

Web前端安全问题分类综合以及XSS、CSRF、SQL注入、DoS/DDoS攻击、会话劫持、点击劫持等详解，增强生产安全意识

前端安全问题是指发生在浏览器、单页面应用、Web页面等前端环境中的各类安全隐患。Web前端作为与用户直接交互的界面&#xff0c;其安全性问题直接关系到用户体验和数据安全。近年来&#xff0c;随着前端技术的快速发展&#xff0c;Web前端安全问题也日益凸显。因此&#xff0c…...

编程日记 2024/6/9 15:08:21

1.单选题 (2分)下列关于脚本的说法不正确的是( )。本题得分： 2分正确答案： A2.单选题 (2分)软件测试自动化的局限性不包含( )。本题得分： 2分

1.单选题 (2分) 下列关于脚本的说法不正确的是( )。 A 线性脚本是最复杂的脚本 B 结构化脚本具有较好的可读性、可重用性,易于维护 C 关键字驱动脚本在开发时,不关心基础函数,直接使用已定义好的关键字 D 数据驱动脚本将测试脚本和数据进行分离,同一个脚本可以针对不同的输…...

编程日记 2024/6/9 15:06:18

【Docker系列】跨平台 Docker 镜像构建：深入理解`--platform`参数

&#x1f49d;&#x1f49d;&#x1f49d;欢迎来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

编程日记 2024/6/9 15:05:17

力扣1248.统计优美子数组

力扣1248.统计优美子数组 同930. 哈希表法 求前缀和 class Solution {public:int numberOfSubarrays(vector<int>& nums, int k) {int n nums.size();unordered_map<int,int> cnt;int res0,sum0;for(int i0,j0;i<n;i){cnt[sum] ;if(nums[i] & 1) …...

编程日记 2024/6/9 15:04:16

AI2THOR 2.1.0使用教程

一、安装和入门 1.1 AI2-THOR使用要求 操作系统&#xff1a; Mac OS X 10.9&#xff0c; Ubuntu 14.04显卡&#xff1a;DX9&#xff08;着色器型号 3.0&#xff09;或 DX11&#xff0c;功能级别为 9.3。CPU&#xff1a;支持 SSE2 指令集。Python 2.7 或 Python 3.5Linux 用户…...

编程日记 2024/6/9 15:02:15

在Nginx中配置php程序环境。

1、前言。 　　我一开始是想 搭建 Tomcat PHP 环境。 　　Tomcat并不能直接运行PHP&#xff0c;因为Tomcat是一个Java Web服务器&#xff0c;主要用于运行Java应用程序。但是&#xff0c;我们可以通过一些配置和工具来使Tomcat能够运行PHP。 　　在配置Tomcat支持PHP 项目的时…...

编程日记 2024/6/9 15:01:13

！力扣70. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢&#xff1f; 1. 递归&#xff08;超时&#xff09; class Solution { public:int climbStairs(int n) {if(n1){return 1;}if(n2){return 2;}return climbStairs…...

编程日记 2024/6/9 15:00:12

Spring boot+vue前后端分离

目录 1、前端vue的搭建 2、后端项目的构建 pom文件中引入的jar包 yml文件用来配置连接数据库和端口的设置 application.property进行一些整合 service层 imp层 mapper 实体类 额外写一个类、解决跨域问题 3、测试 1、前端vue的搭建 建立项目的过程略 开启一个建立好…...

编程日记 2024/6/9 14:59:11

Python基础总结之列表转字符串

Python基础总结之列表转字符串 在Python中&#xff0c;将列表转换为字符串有多种方法&#xff0c;最常用的是使用str.join()方法。这里有一些示例&#xff1a; 使用str.join()方法 这是将列表转换为字符串的最直接和最常用的方法。你需要确保列表中的所有元素都是字符串类型…...

编程日记 2024/6/9 14:58:10

二分【1】二分查找框架 查找指定元素

目录 二分查找 基本思想 几种情况汇总 一。严格递增序列 1.查找本身 2.查找第一个大于等于自己的 3.查找第一个大于自己的 4.严格递减序列 二。有重复元素 1.取其中第一个出现的 2.取其中最后一个出现的 二分查找 基本思想 几种情况汇总 一。严格递增序列 1.查找本身…...

编程日记 2024/6/9 14:57:09

SkyWalking 10.2.0 SWCK 配置过程

SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外&#xff0c;K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案&#xff0c;全安装在K8S群集中。 具体可参…...

编程新知 2025/8/23 5:51:08

相机Camera日志实例分析之二：相机Camx【专业模式开启直方图拍照】单帧流程日志详解

【关注我&#xff0c;后续持续新增专题博文&#xff0c;谢谢&#xff01;&#xff01;&#xff01;】 上一篇我们讲了&#xff1a; 这一篇我们开始讲&#xff1a; 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下&#xff1a; 一、场景操作步骤 操作步…...

编程新知 2026/1/30 10:10:55

学校时钟系统，标准考场时钟系统，AI亮相2025高考，赛思时钟系统为教育公平筑起“精准防线”

2025年#高考 将在近日拉开帷幕&#xff0c;#AI 监考一度冲上热搜。当AI深度融入高考&#xff0c;#时间同步 不再是辅助功能&#xff0c;而是决定AI监考系统成败的“生命线”。 AI亮相2025高考&#xff0c;40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕&#xff0c;江西、…...

编程新知 2026/2/8 22:07:52

Android第十三次面试总结（四大 组件基础）

Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成&#xff0c;用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机&#xff1a; ​onCreate()​​ ​调用时机​&#xff1a;Activity 首次创建时调用。​…...

编程新知 2025/10/15 15:07:34

pycharm 设置环境出错

pycharm 设置环境出错 pycharm 新建项目&#xff0c;设置虚拟环境&#xff0c;出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

编程新知 2026/1/16 15:03:10

jdbc查询mysql数据库时，出现id顺序错误的情况

我在repository中的查询语句如下所示&#xff0c;即传入一个List<intager>的数据&#xff0c;返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致&#xff0c;会导致返回的id是从小到大排列的&#xff0c;但我不希望这样。 Query("SELECT NEW com…...

编程新知 2026/2/4 19:50:05

【把数组变成一棵树】有序数组秒变平衡BST，原来可以这么优雅！

【把数组变成一棵树】有序数组秒变平衡BST，原来可以这么优雅！ 🌱 前言：一棵树的浪漫，从数组开始说起 程序员的世界里，数组是最常见的基本结构之一，几乎每种语言、每种算法都少不了它。可你有没有想过，一组看似“线性排列”的有序数组，竟然可以**“长”成一棵平衡的二…...

编程新知 2025/8/26 4:33:55

Python学习(8) ----- Python的类与对象

Python 中的类&#xff08;Class&#xff09;与对象&#xff08;Object&#xff09;是面向对象编程&#xff08;OOP&#xff09;的核心。我们可以通过“类是模板&#xff0c;对象是实例”来理解它们的关系。 &#x1f9f1; 一句话理解&#xff1a; 类就像“图纸”&#xff0c;对…...

编程新知 2025/10/23 12:11:37

Go爬虫开发学习记录

Go爬虫开发学习记录 基础篇&#xff1a;使用net/http库 Go的标准库net/http提供了完善的HTTP客户端功能&#xff0c;是构建爬虫的基石&#xff1a; package mainimport ("fmt""io""net/http" )func fetchPage(url string) string {// 创建自定…...

编程新知 2025/12/27 3:34:57

鸿蒙APP测试实战：从HDC命令到专项测试

普通APP的测试与鸿蒙APP的测试有一些共同的特征&#xff0c;但是也有一些区别&#xff0c;其中共同特征是&#xff0c;它们都可以通过cmd的命令提示符工具来进行app的性能测试。 其中区别主要是&#xff0c;对于稳定性测试的命令的区别&#xff0c;性能指标获取方式的命令的区…...

编程新知 2026/2/4 3:42:04