1奇函数偶函数
文章目录
- 自变量
- 有理化
- 奇偶性
- 周期性
- 初等函数
自变量
自变量是x,这个还挺奇怪,记住就好
y = f ( e x + 1 ) y=f(e^x+1) y=f(ex+1) 里面 e x e^x ex 只算中间变量,自变量是x
做这些题,想到了以前高中的时候做数学题,不够扎实呀,要是足够扎实,绝对不是95分的分数,应该多少也能考个110分(2022年新高考一卷的数学比较难),只能往前看了,现在学知识或者干啥整的扎实一些,我现在回想以前的高中知识,其实不在于刷多少题目,我买了很多刷题的书,其实很多都没写过几个题,白白浪费了,利用好已有的资料,把每一个细节自己慢慢想清楚,应该是对我来说最好的
需要判断一个函数的奇偶性,首先要看定义域是否关于原点对称,虽然感觉考试的时候一般都是对称的
一个分式和零的大小关系,可以转换成乘式和零的大小关系,这个应该是比较自然而然的
老师说一个简单的知识点记不住没办法,以前一个初中英语老师说她记英语单词就一个办法,死记,重复,其实是这样的,用的多了其实怎么都能记住了,有时候说自己记不住只是找个借口罢了,还是用的不够多,比如说你好,这两个汉字,用的非常多,哪怕一个人很久不写字也不至于不会写这两字吧
有理化
看到一个带根号的式子,根号且有加或者减去一个东西,可以考虑分式上下同时乘以一个元素,就是用平方差公式进行分子有理化
奇偶性
双曲正弦,双曲余弦,反双曲正弦,这几个函数都比较常见,但是在电脑上打数学公式比较麻烦,等之后我摸索出来怎么方便的在电脑上打出这些数学公式,我就把这些公式打上来,貌似也是有一些语法,其实我之前写算法题的时候也打过一些,但是现在好久没写算法题了,也差不多忘光了
算了不等以后,就现在就开始用latex打数学公式
F ( x ) = f ( x ) + f ( − x ) 2 偶函数 F(x)=\frac{f(x)+f(-x)}{2} \ \ 偶函数 F(x)=2f(x)+f(−x) 偶函数
F ( x ) = f ( x ) − f ( − x ) 2 奇函数 F(x)=\frac{f(x)-f(-x)}{2} \ \ 奇函数 F(x)=2f(x)−f(−x) 奇函数
上面两个公式记住,在判断奇函数偶函数的时候可能可以更加快速,因为给定的一个复杂函数可能可以拆开变成上面的形式
奇函数和偶函数相乘,或者就是排列组合,乘积得到的函数的奇偶性是什么,其实非常简单,把奇函数看成-1,偶函数看成1就好,之前看到这种结论还以为什么怪力乱神,其实想清楚之后挺简单
看网课,一下子就是两个小时,数据库也是,一看就是很长的时间,没一点儿战略耐心还真受不了
看完这个网课就去看数据库网课
周期性
哈哈有意思,做数学题用比较直观的办法硬算,在老师看来这叫做诱敌深入,比如说一个题,求三阶导数或者五阶导数,直接算确实能算,但是不是最巧妙的,最快速的办法,老师就是想让考生在这儿花一些时间,可能这可以制造一些区分度吧。所以那些在考场上可以快速写完卷子的人,其实不是他们的手速有多快,可能手速也挺快,但不是核心因素,核心因素是解题方法的差异,我们高中年级第一最后去清华的那个同学,据说是发卷子的前五分钟,都还没动笔,第一面生物试卷都全部写完了,开始动笔填完选择题就可以直接翻页
原函数以什么为周期,导函数也以什么为周期
初等函数
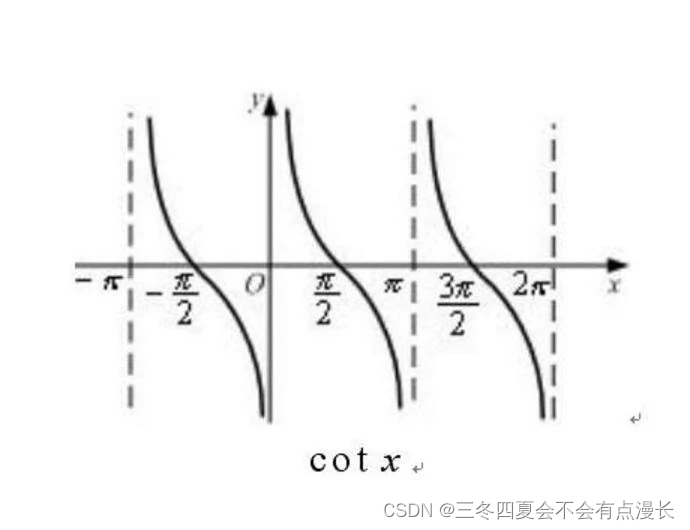
c o t x cot \ x cot x 是奇函数
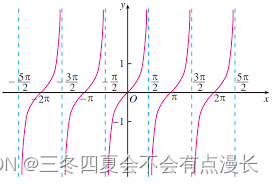
t a n x tan \ x tan x
三角函数里面的割函数确确实实用的相对较少,图像可以不用记住,但是计算的时候需要记住, s e c x = 1 c o s x sec \ x=\frac{1}{cos \ x} sec x=cos x1,数学公式用专业的语法确实会好看一些,下次也不要用 cos x 这种标记,代码这样子写还行,数学的就用这种 c o s x cos \ x cos x ,注意是首字母不一样,求倒数就好,挺方便记忆的
s e c 2 x = 1 + t a n 2 x sec ^2x=1+tan^2x sec2x=1+tan2x
c s c 2 x = 1 + c o t 2 x csc^2x=1+cot^2x csc2x=1+cot2x
上面两个公式比较重要
知识过一遍记不住很正常,先留一个印象,以后需要用的时候,再去查就好了
相关文章:

1奇函数偶函数
文章目录 自变量有理化奇偶性周期性初等函数 自变量 自变量是x,这个还挺奇怪,记住就好 y f ( e x 1 ) yf(e^x1) yf(ex1) 里面 e x e^x ex 只算中间变量,自变量是x 做这些题,想到了以前高中的时候做数学题,不够扎实…...
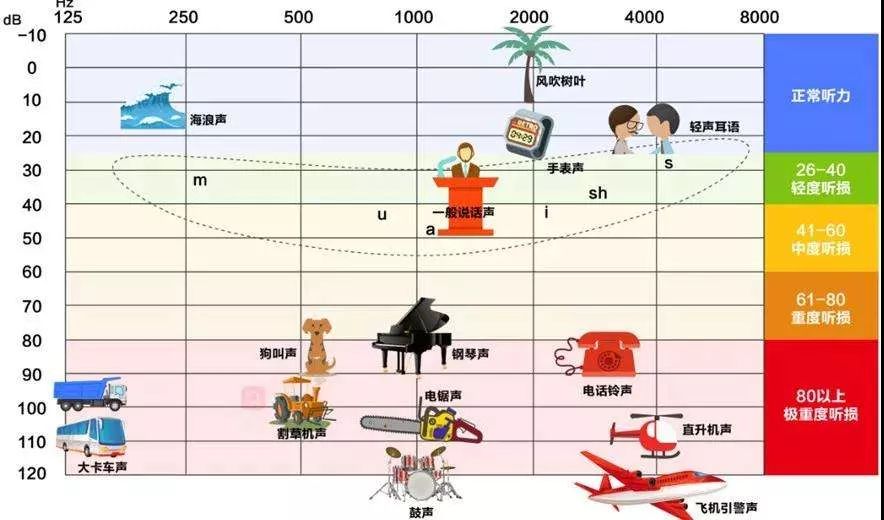
什么情况下需要配戴助听器
以下几种情况需要考虑配戴助听器: 1、听力无波动3个月以上的感音神经性听力障碍。如:先天性听力障碍、老年性听力障碍、噪声性听力障碍、突聋的稳定期等,均可选配合适的助听器。 2、年龄方面。使用助听器没有严格的年龄限制,从出生数周的婴…...
)
Java 基础面试300题 (231-260)
Java 基础面试300题 (231-260) 231 String::toUpperCase是什么类型的方法引用? String::toUpperCase是任意方法引用的示例。它指的是String 类的toUpperCase方法,但不是指任何特定对象。 通常在遍历集合或流时使用。例如&#x…...
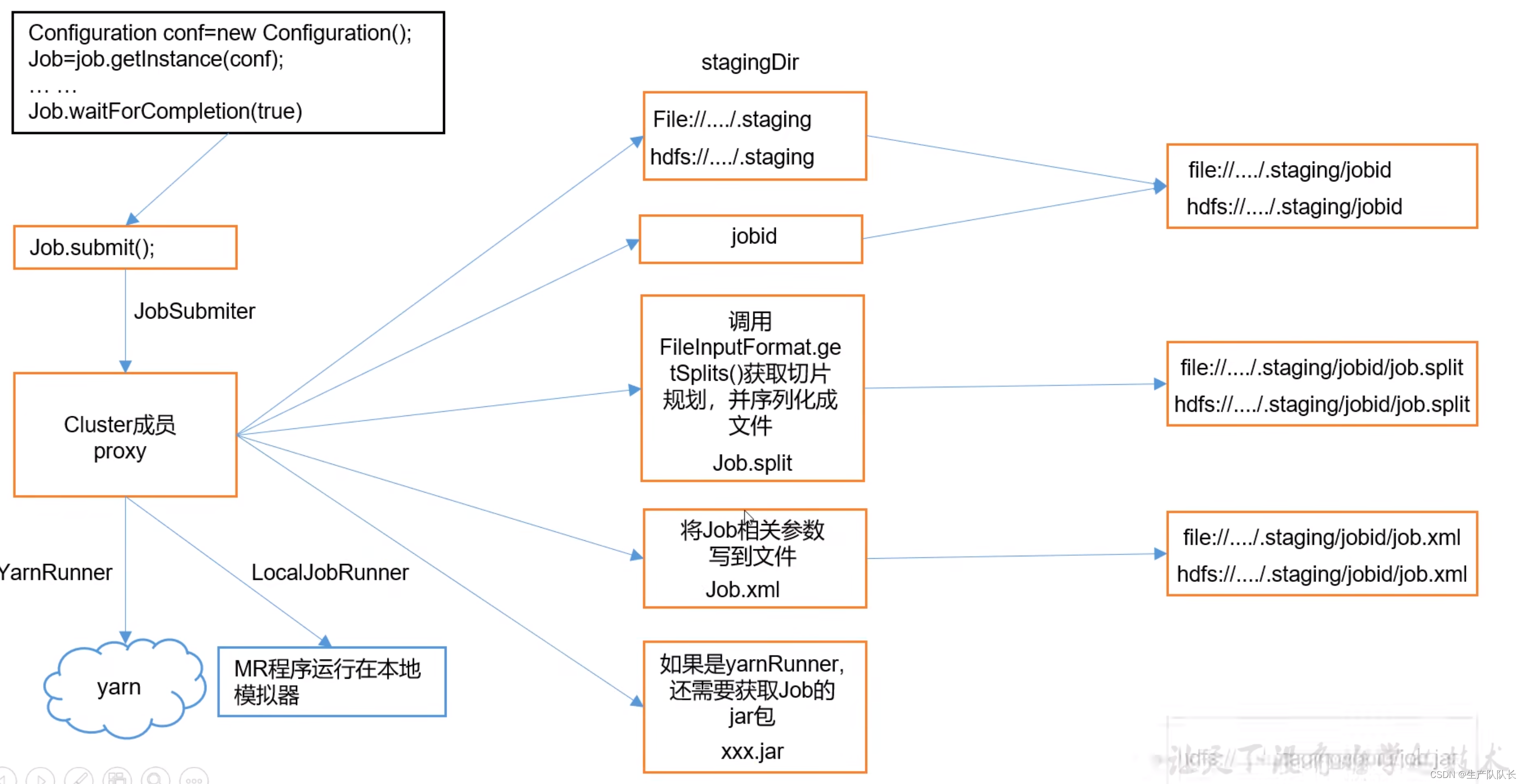
Hadoop3:MapReduce源码解读之Map阶段的Job任务提交流程(1)
3、Job工作机制源码解读 用之前wordcount案例进行源码阅读,debug断点打在Job任务提交时 提交任务前,建立客户单连接 如下图,可以看出,只有两个客户端提供者,一个是YarnClient,一个是LocalClient。 显然&a…...
Linux环境---在线安装MYSQL数据库
Linux环境—在线安装MYSQL数据库 一、使用步骤 1.安装环境 Mysql 驱动 8.0 需要 jdk1.8 才行。 JDK版本:1.8 参考文档 MYSQL版本:8.0.2 下载链接: https://pan.baidu.com/s/1MwXIilSL6EY3OuS7WtpySA?pwdg263 操作系统:CentOS 1.1 建立存…...

git本地配置及IDEA下Git合并部分文件
目录 1、IDEA 下 Git 合并部分文件 2、分支合并忽略特定文件步骤 3、git本地配置 1、IDEA 下 Git 合并部分文件 1.1Git 下存在两个分支,foo 和 bar 分支,想要把 bar 分支上的部分文件合并到 foo 分支: 首先切换到 foo 分支,点击右下角的 …...

安徽京准 NTP时钟同步服务器具体配置方法是什么?
安徽京准 NTP时钟同步服务器具体配置方法是什么? 安徽京准 NTP时钟同步服务器具体配置方法是什么? 可以使用特权终结点 (PEP) 来更新 Azure Stack Hub 中的时间服务器。 使用可解析为两个或更多个 NTP(网络时间协议)服务器 IP 地…...

微信小程序 画布canvas
属性说明 属性类型默认值必填说明最低版本typestring否指定 canvas 类型,支持 2d (2.9.0) 和 webgl (2.7.0)2.7.0canvas-idstring否canvas 组件的唯一标识符,若指定了 type 则无需再指定该属性1.0.0disable-scrollbooleanfalse否当在 canvas 中移动时且…...

leetcode-04-[24]两两交换链表中的节点[19]删除链表的倒数第N个节点[160]相交链表[142]环形链表II
一、[24]两两交换链表中的节点 重点:暂存节点 class Solution {public ListNode swapPairs(ListNode head) {ListNode dummyHeadnew ListNode(-1);dummyHead.nexthead;ListNode predummyHead;//重点:存节点while(pre.next!null&&pre.next.next…...

深入探讨 Java 18 的主要新特性,分析其设计理念和实际应用
Java 18 作为 Java 的最新版本,引入了一系列的新特性和改进,这些变化不仅提升了语言的性能和安全性,也为开发者提供了更多的工具和选项,简化了开发过程,提高了代码的可读性和维护性。本文将深入探讨 Java 18 的主要新特性,分析其设计理念和实际应用,帮助读者理解这些新特…...
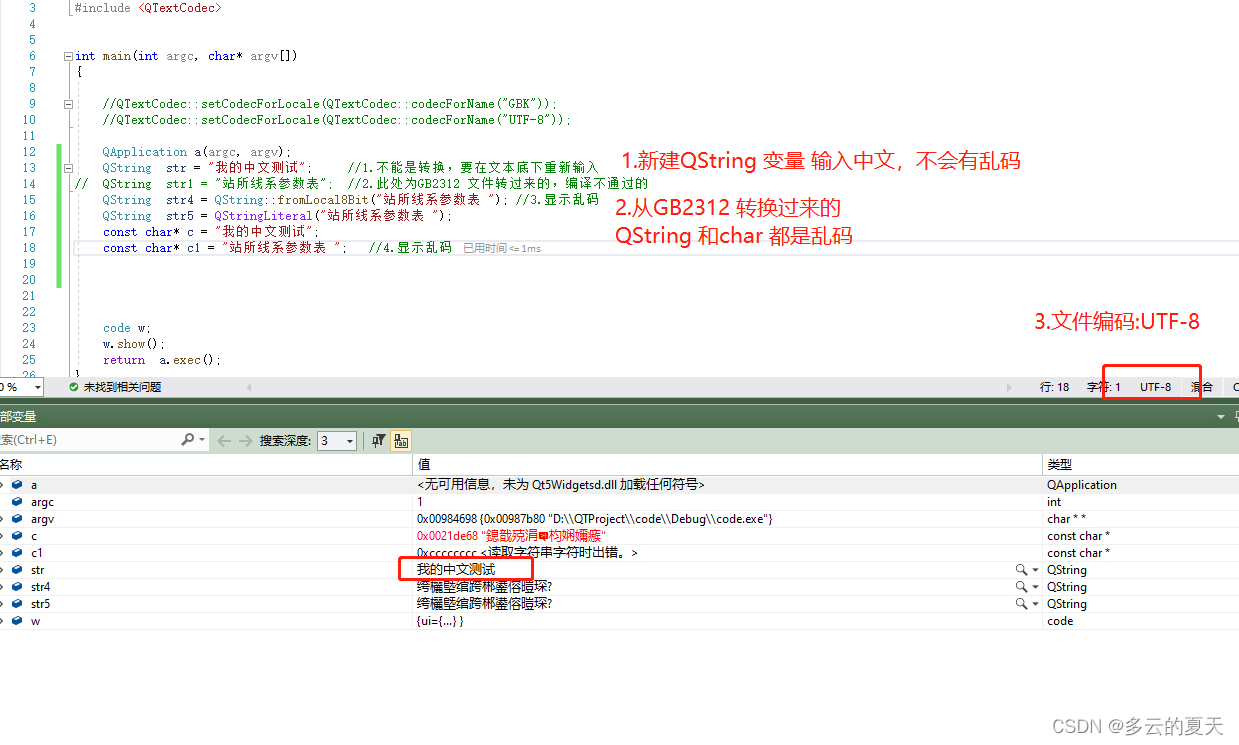
qt4-qt5 升级(2)-GUI-UTF-8-GBK-QTextCode-字符集乱码
MFC与QT的消息机制的区别_qt信号槽机制与mfc的消息映射机制的区别-CSDN博客 1.QT4-QT5差别 kits构建 控件,信号与槽 ui修改好后点击编译会自动生成 ui_XXX.h 聚合的关系,不是拥有的关系。 QWidget 和QWindow有什么差别? 2.VS2019-QT5 构建…...

Qt Designer 生成的 .ui 文件转为 .py 文件并运行
1. 使用使用 PyUIC将 .ui 转 .py (1)打开命令行终端(可以用cmd,或pycharm 下面的 Terminal)。 (2)导航到包含.ui文件的目录。 cd 你的ui文件路径 (3)运行以下命令来…...
Dubbo 3.x源码(20)—Dubbo服务引用源码(3)
基于Dubbo 3.1,详细介绍了Dubbo服务的发布与引用的源码。 此前我们学习了调用createProxy方法,根据服务引用参数map创建服务接口代理引用对象的整体流程,我们知道会调用createInvokerForRemote方法创建远程引用Invoker,这是Dubbo …...

开发一个Dapp需要多少?
区块链开发一个Dapp要多少钱? 开发一个去中心化应用(Dapp)的成本取决于多个因素,包括Dapp的复杂性、功能需求、区块链平台以及开发团队的经验水平。以下是一些主要的影响因素: 1. 区块链平台:不同区块链…...
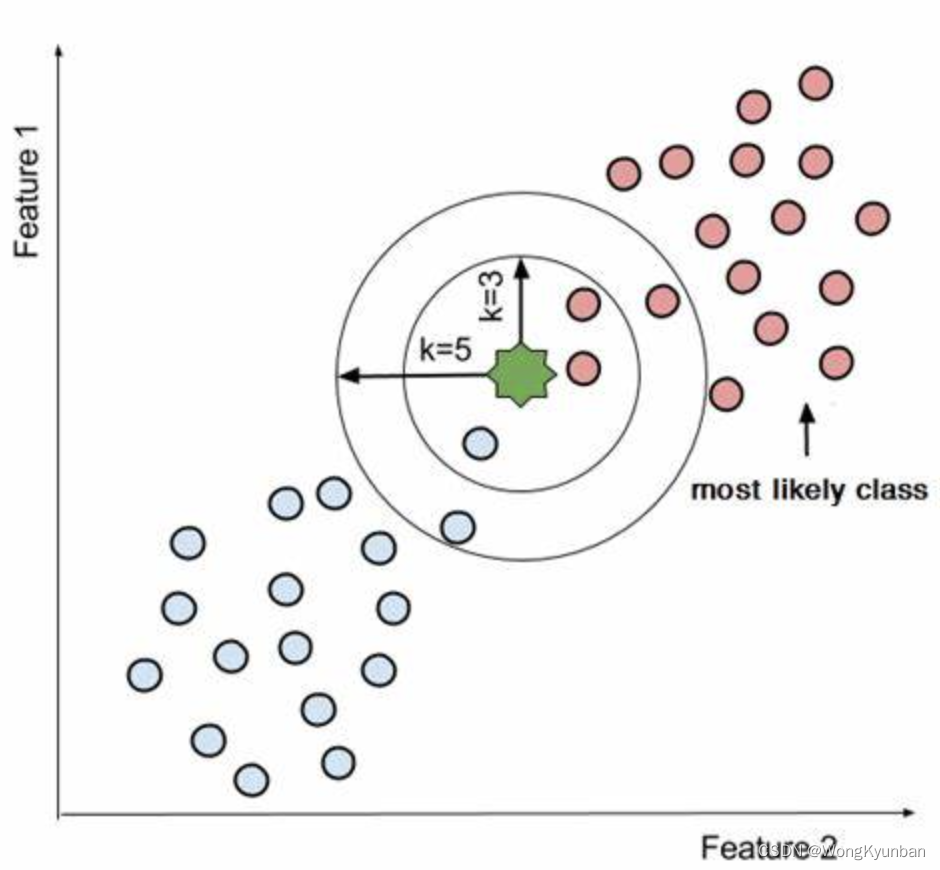
kNN算法-概述
所谓kNN算法就是K-nearest neigbor algorithm。这是似乎是最简单的监督机器学习算法。在训练阶段,kNN算法存储了标签训练样本数据。简单地说,就是调用训练方法时传递给它的标签训练样本会被它存储起来。 kNN算法也叫lazy learning algorithm懒惰学习算法…...

富格林:曝光纠正出金亏损陋习
富格林悉知,虽然现货黄金市场看似变化无常,在操作方向上依旧是有迹可循的,投资者需要了解曝光的专业经验纠正陋习阻止出金亏损。要获得优质的黄金投资出金效果,就需要在明确现货黄金操作技巧的前提下,只有规范遵循已曝…...
怎么用微信小程序实现远程控制空调
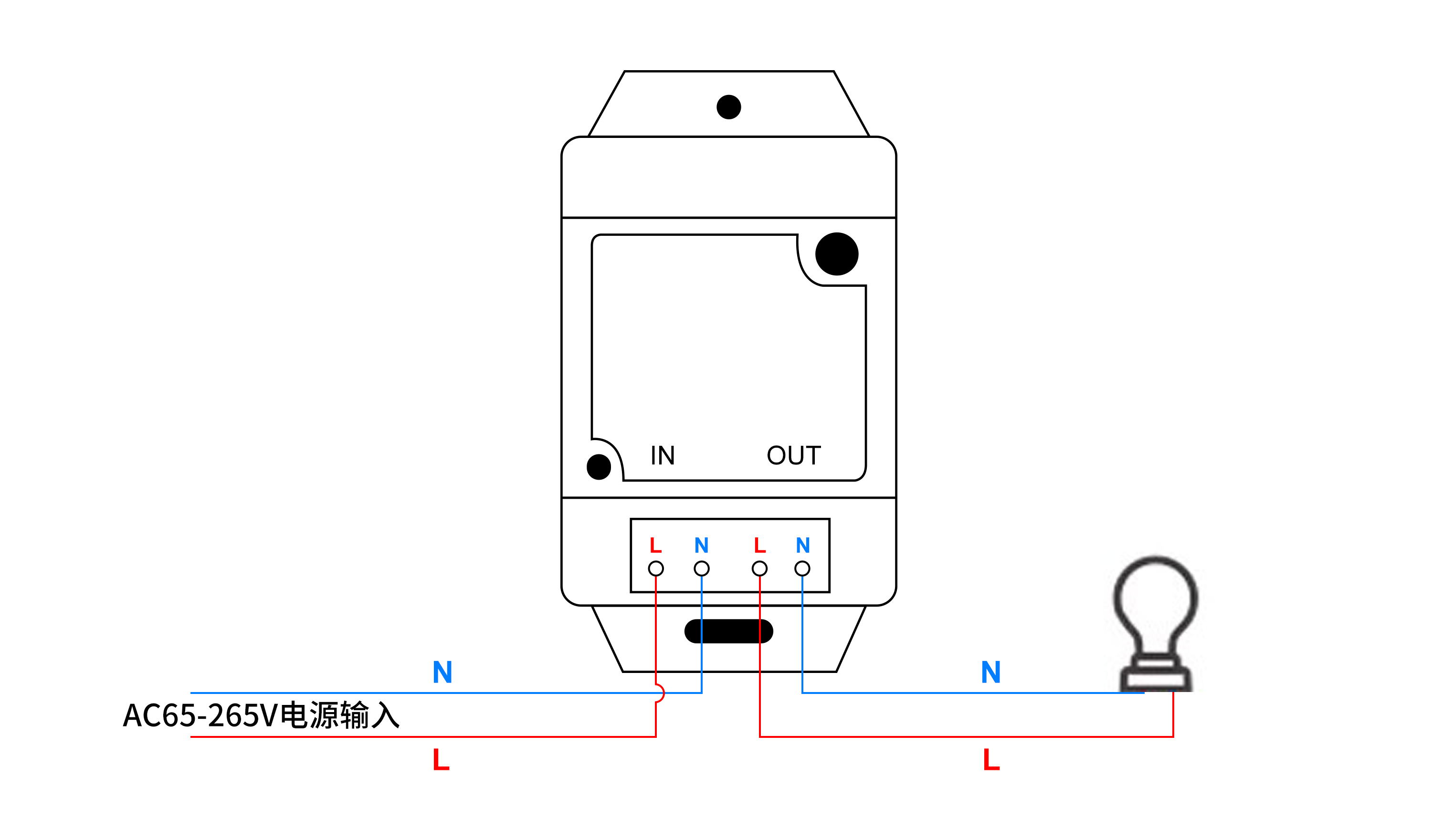
怎么用微信小程序实现远程控制空调呢? 本文描述了使用微信小程序调用HTTP接口,实现控制空调,通过不同规格的通断器,来控制不同功率的空调的电源。 可选用产品:可根据实际场景需求,选择对应的规格 序号设备…...

ES5/ES6 的继承除了写法以外还有什么区别?
一、主要区别 ES5 的继承实质上是先创建子类的实例对象, 然后再将父类的方法添加 到 this 上(Parent.apply(this)) . ES6 的继承机制完全不同, 实质上是先创建父类的实例对象 this(所以必 须先调用父类的 super()方法…...

LeetCode 第401场周赛个人题解
100325. 找出 K 秒后拿着球的孩子 原题链接 100325. 找出 K 秒后拿着球的孩子 思路分析 数据很小,暴力或者数学方法都行 数学方法就是对 n - 1做带余除法,看跑了奇数还是偶数趟,余数如何,确定位置 时间复杂度:O(…...

C#面:请解释web.config⽂件中的重要节点
在C#中,web.config文件是一个XML格式的配置文件,用于配置ASP.NET应用程序的各种设置。web.config文件中包含了许多重要的节点,下面是一些常见的重要节点及其作用: <configuration>节点:web.config文件的根节点&…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
