2024 Jiangsu Collegiate Programming Contest E. Divide 题解 主席树
Divide
题目描述
Given an integer sequence a 1 , a 2 , … , a n a_1,a_2,\ldots,a_n a1,a2,…,an of length n n n. For an interval a l , … , a r a_l,\ldots,a_r al,…,ar in this sequence, a Reduce operation divides the maximum value of the interval by 2 2 2 (rounding down). If there are multiple maximum values, choose the one with the smallest index. There are q q q queries. Given three integers l , r , k l,r,k l,r,k each time, query the maximum value of the interval after performing k k k Reduce operations on the a l , … , a r a_l,\ldots,a_r al,…,ar interval. The queries are independent of each other. That is to say, each time the query starts from the initially given sequence.
输入描述
The two integers n , q n,q n,q ( 1 ≤ n , q ≤ 1 0 5 1\le n,q\le 10^5 1≤n,q≤105) in the first line represent the sequence length and the number of queries.
The second line contains n n n integers a 1 , a 2 , … , a n a_1,a_2,\ldots,a_n a1,a2,…,an ( 0 ≤ a i ≤ 1 0 5 0\le a_i\le 10^5 0≤ai≤105).
The next q q q lines each have three integers l , r , k l,r,k l,r,k ( 1 ≤ l ≤ r ≤ n , 0 ≤ k ≤ 1 0 9 1\le l\le r\le n,0\le k\le 10^9 1≤l≤r≤n,0≤k≤109), representing a query.
输出描述
For each query, output an integer in one line, representing the maximum value of the interval since the operation started from the initial sequence.
样例 #1
样例输入 #1
3 2
2 0 2
2 3 0
1 3 0
样例输出 #1
2
2
样例 #2
样例输入 #2
6 6
9 5 0 3 6 7
1 4 7
3 3 233
6 6 0
3 4 4
4 5 15
1 1 0
样例输出 #2
1
0
7
0
0
9
思路
将题目所给数组进行扩充。例如,对于样例#2,数组 9 5 0 3 6 7 可通过对每个数不断除以 2 2 2 直至为 0 0 0 ( 0 0 0也加入扩充后数组) 扩充为 9 4 2 1 0 5 2 1 0 0 3 1 0 6 3 1 0 7 3 1 0。这样,对于每个询问,相当于在扩充后的数组中寻找第 k + 1 k+1 k+1 大值。但由于询问中的区间是原数组中的区间,所以我们需利用 map 构建原数组区间到扩充后数组区间的映射。此外,对于询问中 k + 1 k+1 k+1 的值大于扩充后区间中元素个数的情况,需要特判答案为 0 0 0。
代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
typedef long long ll;const int maxn = 2e6;int tot, n, m;
int sum[(maxn << 5) + 10], rt[maxn + 10], ls[(maxn << 5) + 10], rs[(maxn << 5) + 10];
int a[maxn + 10], ind[maxn + 10], len;int getid(const int &val)
{return lower_bound(ind + 1, ind + len + 1, val) - ind;
}int build(int l, int r)
{int root = ++tot;if (l == r){return root;}int mid = l + r >> 1;ls[root] = build(l, mid);rs[root] = build(mid + 1, r);return root;
}int update(int k, int l, int r, int root)
{int dir = ++tot;ls[dir] = ls[root], rs[dir] = rs[root];sum[dir] = sum[root] + 1;if (l == r){return dir;}int mid = l + r >> 1;if (k <= mid){ls[dir] = update(k, l, mid, ls[dir]);}else{rs[dir] = update(k, mid + 1, r, rs[dir]);}return dir;
}int query(int u, int v, int l, int r, int k)
{int mid = l + r >> 1;int x = sum[ls[v]] - sum[ls[u]];if (l == r){return l;}if (k <= x){return query(ls[u], ls[v], l, mid, k);}else{return query(rs[u], rs[v], mid + 1, r, k - x);}
}map<int, pair<int, int>> mp; // 构建原来数组中下标到扩充后数组中下标的映射void init()
{cin >> n >> m;int idx = 0; // 扩充数组的索引int x;for (int i = 1; i <= n; i++){cin >> x;mp[i].first = idx + 1; // 一个原数组中的元素x经扩充后的区间的左端点while (x) // 元素x扩充,扩充到区间[mp[i].first,mp[i].second]里面{a[++idx] = x;x /= 2;}a[++idx] = 0; // ai可能等于0,所以要单独将0加入扩充后区间mp[i].second = idx; // 一个原数组中的元素x经扩充后的区间的右端点}// 离散化构建主席树,主席树可用来求出扩充后数组的区间第k小值memcpy(ind, a, sizeof(ind));sort(ind + 1, ind + idx + 1);len = unique(ind + 1, ind + idx + 1) - ind - 1;rt[0] = build(1, len);for (int i = 1; i <= idx; i++){rt[i] = update(getid(a[i]), 1, len, rt[i - 1]);}
}int l, r, k;void work()
{while (m--){cin >> l >> r >> k;k++; // 当k=i时,求的是第i+1大数,所以k需要++// 主席树询问区间:左开右闭int left = mp[l].first - 1;int right = mp[r].second;// 因为左开右闭,所以区间长度即为right-left,而当区间长度小于k+1时,第k+1大值一定为0if (right - left < k)cout << 0 << '\n';elsecout << ind[query(rt[left], rt[right], 1, len, right - left + 1 - k)] << '\n'; // right - left + 1 - k的运算是将求第k大值转化为求第right - left + 1 - k小值}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);init();work();return 0;
}
相关文章:

2024 Jiangsu Collegiate Programming Contest E. Divide 题解 主席树
Divide 题目描述 Given an integer sequence a 1 , a 2 , … , a n a_1,a_2,\ldots,a_n a1,a2,…,an of length n n n. For an interval a l , … , a r a_l,\ldots,a_r al,…,ar in this sequence, a Reduce operation divides the maximum value of the inter…...
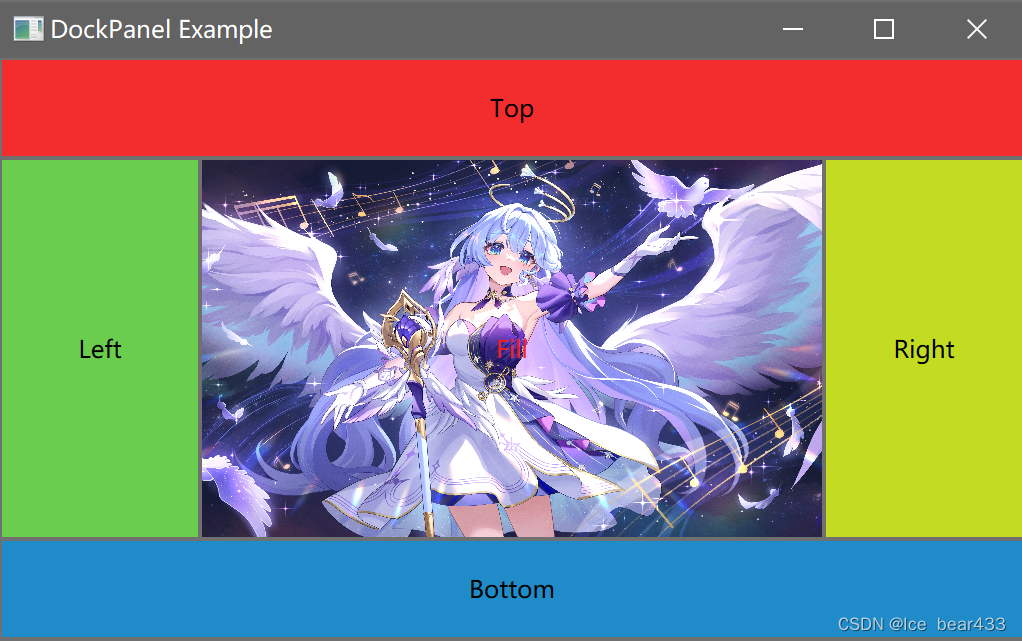
C# WPF入门学习主线篇(十五)—— DockPanel布局容器
C# WPF入门学习主线篇(十五)—— DockPanel布局容器 欢迎来到C# WPF入门学习系列的第十五篇。在前几篇文章中,我们探讨了 Canvas、StackPanel 和 WrapPanel 布局容器及其使用方法。本篇博客将介绍另一种强大且常用的布局容器——DockPanel。…...

基于SVPWM矢量控制的无速度传感器电机控制系统simulink建模与仿真
目录 1.课题概述 2.系统仿真结果 3.核心程序与模型 4.系统原理简介 5.完整工程文件 1.课题概述 基于SVPWM矢量控制的无速度传感器电机控制系统simulink建模与仿真,包括电机,SVPWM模块,矢量控制器模块等。 2.系统仿真结果 3.核心程序与模…...

Linux操作系统:Zookeeper在虚拟环境下的安装与部署
将 Zookeeper 安装到指定目录 // 将zookeeper解压到安装目录 $ tar –zxvf zookeeper-3.4.10.tar.gz –C /usr/local $ mv /usr/local/zookeeper-3.4.10.tar.gz /usr/local/zookeeper 设置 zookeeper 配置文件 // 创建 data 数据目录 $ mkdir /usr/local/zookeeper/data // …...

决策树Decision Tree
目录 一、介绍发展优点缺点基本原理 二、熵1、熵2、条件熵3、信息增益4、信息增益率 三、基尼系数四、ID3算法1、建树过程2、优点3、缺点 五、C4.51、二分法处理连续变量1、流程:2、示例 2、缺点 六、CART1、连续数据处理2、离散数据处理3、CART回归原理1、均方误差…...
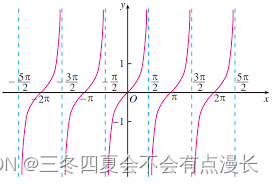
1奇函数偶函数
文章目录 自变量有理化奇偶性周期性初等函数 自变量 自变量是x,这个还挺奇怪,记住就好 y f ( e x 1 ) yf(e^x1) yf(ex1) 里面 e x e^x ex 只算中间变量,自变量是x 做这些题,想到了以前高中的时候做数学题,不够扎实…...
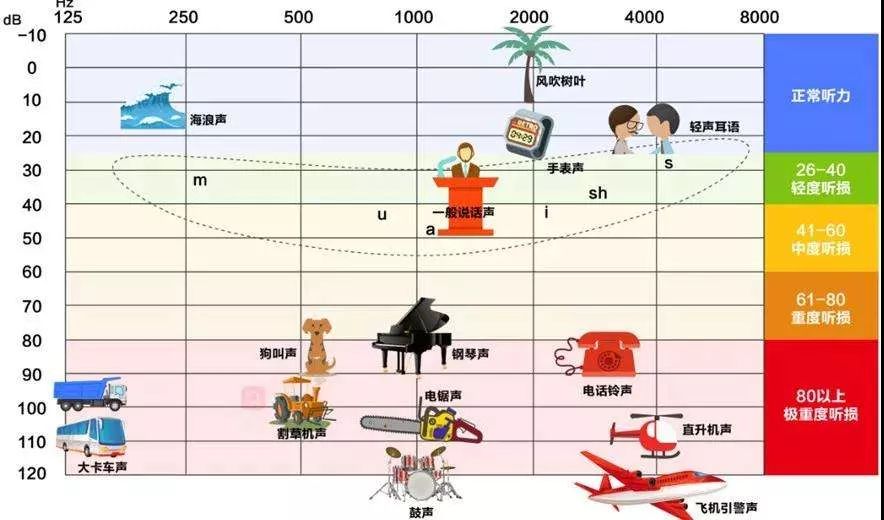
什么情况下需要配戴助听器
以下几种情况需要考虑配戴助听器: 1、听力无波动3个月以上的感音神经性听力障碍。如:先天性听力障碍、老年性听力障碍、噪声性听力障碍、突聋的稳定期等,均可选配合适的助听器。 2、年龄方面。使用助听器没有严格的年龄限制,从出生数周的婴…...
)
Java 基础面试300题 (231-260)
Java 基础面试300题 (231-260) 231 String::toUpperCase是什么类型的方法引用? String::toUpperCase是任意方法引用的示例。它指的是String 类的toUpperCase方法,但不是指任何特定对象。 通常在遍历集合或流时使用。例如&#x…...
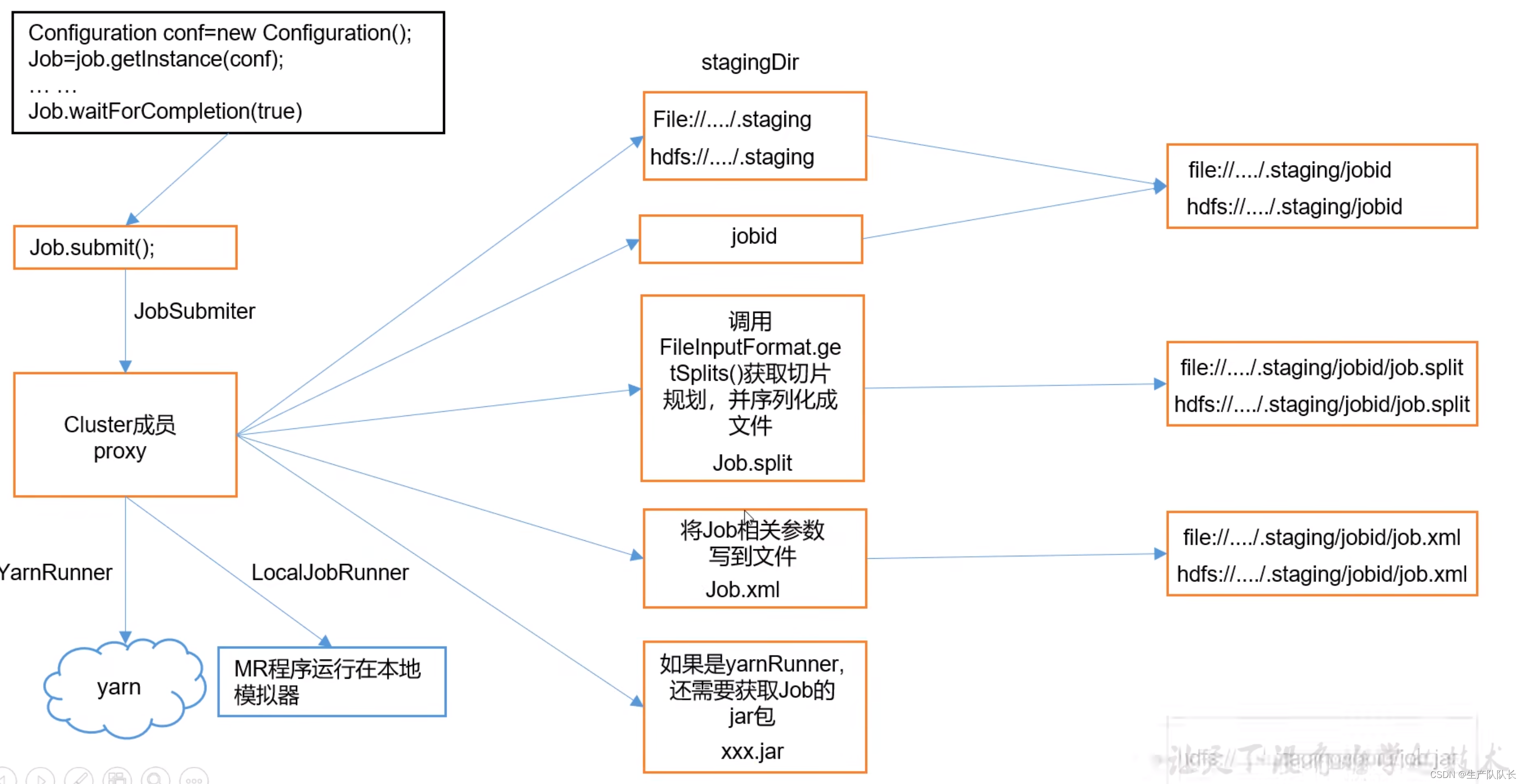
Hadoop3:MapReduce源码解读之Map阶段的Job任务提交流程(1)
3、Job工作机制源码解读 用之前wordcount案例进行源码阅读,debug断点打在Job任务提交时 提交任务前,建立客户单连接 如下图,可以看出,只有两个客户端提供者,一个是YarnClient,一个是LocalClient。 显然&a…...
Linux环境---在线安装MYSQL数据库
Linux环境—在线安装MYSQL数据库 一、使用步骤 1.安装环境 Mysql 驱动 8.0 需要 jdk1.8 才行。 JDK版本:1.8 参考文档 MYSQL版本:8.0.2 下载链接: https://pan.baidu.com/s/1MwXIilSL6EY3OuS7WtpySA?pwdg263 操作系统:CentOS 1.1 建立存…...

git本地配置及IDEA下Git合并部分文件
目录 1、IDEA 下 Git 合并部分文件 2、分支合并忽略特定文件步骤 3、git本地配置 1、IDEA 下 Git 合并部分文件 1.1Git 下存在两个分支,foo 和 bar 分支,想要把 bar 分支上的部分文件合并到 foo 分支: 首先切换到 foo 分支,点击右下角的 …...

安徽京准 NTP时钟同步服务器具体配置方法是什么?
安徽京准 NTP时钟同步服务器具体配置方法是什么? 安徽京准 NTP时钟同步服务器具体配置方法是什么? 可以使用特权终结点 (PEP) 来更新 Azure Stack Hub 中的时间服务器。 使用可解析为两个或更多个 NTP(网络时间协议)服务器 IP 地…...

微信小程序 画布canvas
属性说明 属性类型默认值必填说明最低版本typestring否指定 canvas 类型,支持 2d (2.9.0) 和 webgl (2.7.0)2.7.0canvas-idstring否canvas 组件的唯一标识符,若指定了 type 则无需再指定该属性1.0.0disable-scrollbooleanfalse否当在 canvas 中移动时且…...

leetcode-04-[24]两两交换链表中的节点[19]删除链表的倒数第N个节点[160]相交链表[142]环形链表II
一、[24]两两交换链表中的节点 重点:暂存节点 class Solution {public ListNode swapPairs(ListNode head) {ListNode dummyHeadnew ListNode(-1);dummyHead.nexthead;ListNode predummyHead;//重点:存节点while(pre.next!null&&pre.next.next…...

深入探讨 Java 18 的主要新特性,分析其设计理念和实际应用
Java 18 作为 Java 的最新版本,引入了一系列的新特性和改进,这些变化不仅提升了语言的性能和安全性,也为开发者提供了更多的工具和选项,简化了开发过程,提高了代码的可读性和维护性。本文将深入探讨 Java 18 的主要新特性,分析其设计理念和实际应用,帮助读者理解这些新特…...
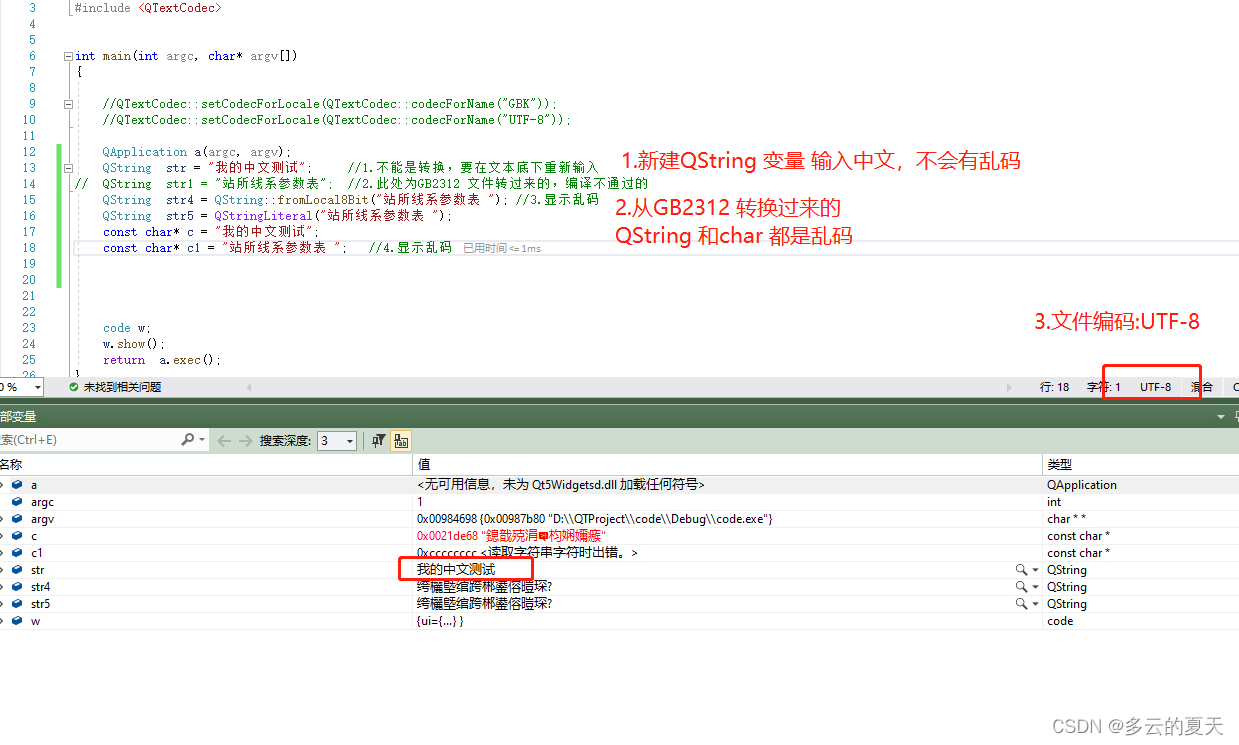
qt4-qt5 升级(2)-GUI-UTF-8-GBK-QTextCode-字符集乱码
MFC与QT的消息机制的区别_qt信号槽机制与mfc的消息映射机制的区别-CSDN博客 1.QT4-QT5差别 kits构建 控件,信号与槽 ui修改好后点击编译会自动生成 ui_XXX.h 聚合的关系,不是拥有的关系。 QWidget 和QWindow有什么差别? 2.VS2019-QT5 构建…...

Qt Designer 生成的 .ui 文件转为 .py 文件并运行
1. 使用使用 PyUIC将 .ui 转 .py (1)打开命令行终端(可以用cmd,或pycharm 下面的 Terminal)。 (2)导航到包含.ui文件的目录。 cd 你的ui文件路径 (3)运行以下命令来…...
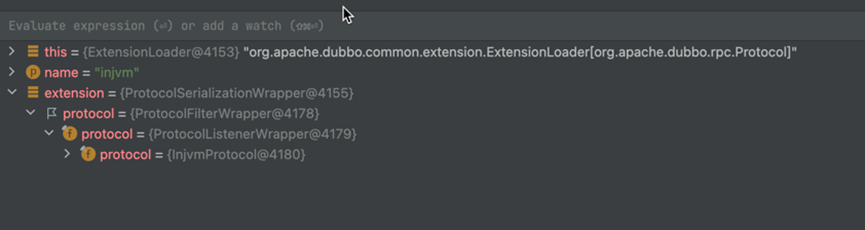
Dubbo 3.x源码(20)—Dubbo服务引用源码(3)
基于Dubbo 3.1,详细介绍了Dubbo服务的发布与引用的源码。 此前我们学习了调用createProxy方法,根据服务引用参数map创建服务接口代理引用对象的整体流程,我们知道会调用createInvokerForRemote方法创建远程引用Invoker,这是Dubbo …...

开发一个Dapp需要多少?
区块链开发一个Dapp要多少钱? 开发一个去中心化应用(Dapp)的成本取决于多个因素,包括Dapp的复杂性、功能需求、区块链平台以及开发团队的经验水平。以下是一些主要的影响因素: 1. 区块链平台:不同区块链…...
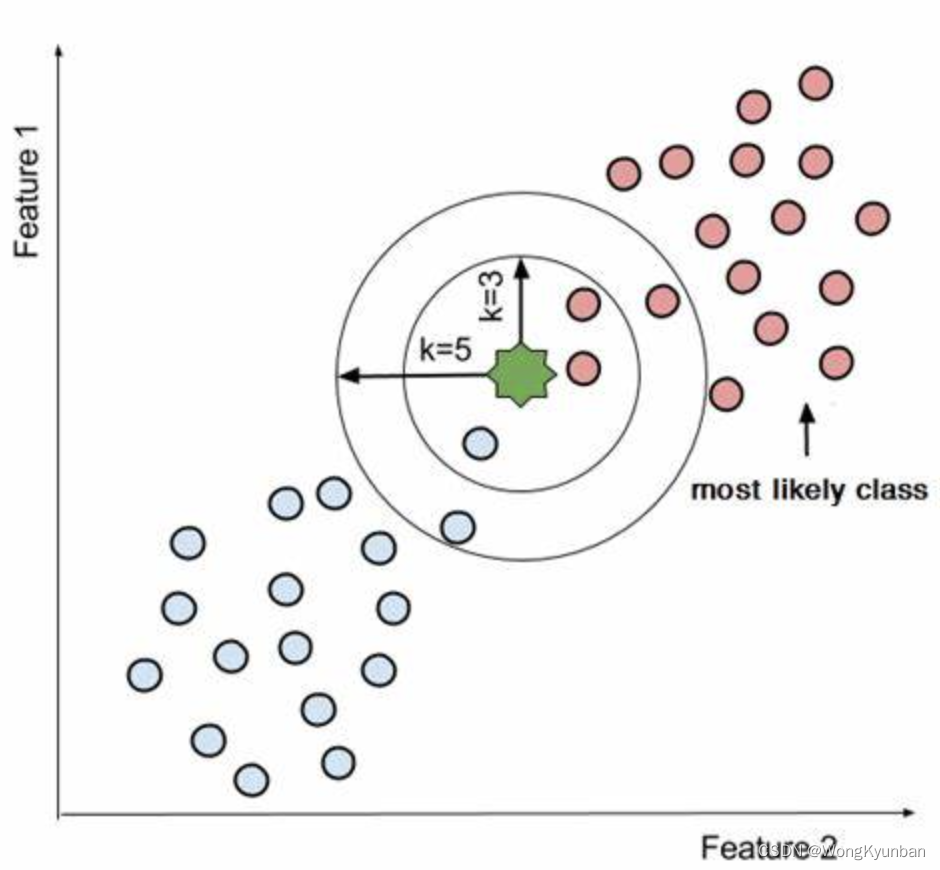
kNN算法-概述
所谓kNN算法就是K-nearest neigbor algorithm。这是似乎是最简单的监督机器学习算法。在训练阶段,kNN算法存储了标签训练样本数据。简单地说,就是调用训练方法时传递给它的标签训练样本会被它存储起来。 kNN算法也叫lazy learning algorithm懒惰学习算法…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...
