代码随想录 | Day17 | 二叉树:二叉树的最大深度最小深度
代码随想录 | Day17 | 二叉树:二叉树的最大深度&&最小深度
主要学习内容:
利用前序后序层序求解二叉树深度问题
其中穿插回溯法
104.二叉树的最大深度
104. 二叉树的最大深度 - 力扣(LeetCode)
递归遍历
后序遍历
1.递归函数参数和返回值
使用后序遍历一般都是上层需要使用下层函数的返回值
本道题目是返回值表示该子树的最大深度,所以为int
函数参数就是当前结点
int r(TreeNode *t)
2.确定终止条件
遇到空指针说明结束这层函数
if(t==nullptr)return 0;
3.本层逻辑
定义上
返回值是这棵子树的最大深度
所以记录左右子树的最大深度然后取最大值再加上本层就是自身的最大深度然后返回即可
int left=r(t->left);int right=r(t->right);int res=1+max(left,right);return res;
完整代码:
class Solution {
public:int r(TreeNode *t){if(t==nullptr)return 0;int left=r(t->left);int right=r(t->right);int res=1+max(left,right);return res;}int maxDepth(TreeNode* root) {return r(root);}
};
class Solution {
public:int r(TreeNode *t){if(t==nullptr)return 0;return 1+max(r(t->left),r(t->right));}int maxDepth(TreeNode* root) {return r(root);}
};
前序遍历
其实就是回溯法
1.确定函数参数和返回值
不需要返回值,参数就是当前节点,记录最大值由全局变量完成(函数参数也可以完成,两者等价)
2.终止条件
如果当前节点左右孩子都为空说明深度就到这里为止了
3.本层处理逻辑
就是遍历本层的结点,这是二叉树所以只有左右孩子两个用两个if来表示遍历即可
(如果做过回溯篇会知道应该此处对应是for循环)
然后左不为空,深度++,继续遍历,函数结束后还原现场
然后右边一样
if(t->left){res++;r(t->left);res--;}if(t->right){res++;r(t->right);res--;}
完整代码:
class Solution {
public:int res,result;void r(TreeNode *t){if(t->left==nullptr&&t->right==nullptr){result=max(res,result);return;}if(t->left){res++;r(t->left);res--;}if(t->right){res++;r(t->right);res--;}}int maxDepth(TreeNode* root) {res=1;result=0;if (root == NULL) return result;r(root);return result;}
};
层序遍历
还是套用之前的模板就行,不做过多的赘述
559.N叉树的最大深度
559. N 叉树的最大深度 - 力扣(LeetCode)
后序遍历
和刚刚思路一模一样,模仿着写就行
class Solution {
public:int r(Node *t){int depth=0;if(t==nullptr)return 0;for(auto c:t->children){int res=r(c);depth=max(depth,res+1);}return depth;}int maxDepth(Node* root) {if(root==nullptr)return 0;return r(root)+1;}
};
前序遍历
也和前面一样,差别就是前面是左右子树,而这里是for循环
class Solution {
public:int res;void r(Node *t,int depth){res=max(depth,res);for(auto c:t->children)r(c,depth+1);}int maxDepth(Node* root) {if(root==nullptr)return 0;res=0;r(root,1);return res;}
};
层序遍历
也还是套模板就行
111.二叉树最小深度
111. 二叉树的最小深度 - 力扣(LeetCode)
后序遍历
和最大深度的区别就是左孩子为空右孩子不为空和左不为空右为空的逻辑处理,剩下的都一样
class Solution {
public:int r(TreeNode *t){if (t == nullptr) return 0;int left=r(t->left);int right=r(t->right);//左为空右不为空 返回右边最小深度+1if(t->left==nullptr&&t->right!=nullptr)return right+1;//左不为空右为空 返回左边最小深度+1if(t->left!=nullptr&&t->right==nullptr)return left+1;int res=1+min(left,right);return res;}int minDepth(TreeNode* root) {if(root==nullptr)return 0;return r(root);}
};
前序遍历
和之前一模一样
class Solution {
public:int res;void r(TreeNode *t,int depth){if(t->right==nullptr&&t->left==nullptr){res=min(depth,res);return;}if(t->left){depth++;r(t->left,depth);depth--;}if(t->right){depth++;r(t->right,depth);depth--;}}int minDepth(TreeNode* root) {if(root==nullptr)return 0;res=0x3f3f3f3f;r(root,1);return res;}
};
相关文章:

代码随想录 | Day17 | 二叉树:二叉树的最大深度最小深度
代码随想录 | Day17 | 二叉树:二叉树的最大深度&&最小深度 主要学习内容: 利用前序后序层序求解二叉树深度问题 其中穿插回溯法 104.二叉树的最大深度 104. 二叉树的最大深度 - 力扣(LeetCode) 递归遍历 后序遍历 …...

【Linux】Socket编程基础
文章目录 字节序字节序转化函数 套接字socket通用结构体通信类型名空间套接字函数socket():创建套接字bind()函数:绑定服务器套接字与其地址、端口listen()函数:侦听客户连接connect():连接服务器套接字accept()函数:服…...
关于stm32的软件复位
使用软件复位的目的: 软件复位并不会擦除存储器中的数据,它只是将处理器恢复到复位状态,即中断使能位被清除,系统寄存器被重置,但RAM和Flash存储器中的数据保持不变。 STM32软件复位(基于库文件V3.5) ,对…...

规范系统运维:系统性能监控与优化的重要性与实践
在当今这个高度信息化的时代,企业的IT系统运维工作显得尤为关键。其中,系统性能监控和优化是运维工作中不可或缺的一环。本文旨在探讨规范系统运维中系统性能监控与优化的重要性,并分享一些实践经验和策略。 一、系统性能监控与优化的重要性…...

用python编撰一个电脑清理程序
自制一个电脑清理程序,有啥用呢?在电脑不装有清理软件的时候,可以解决自己电脑内存不足的情况。 1、设想需要删除指定文件夹中的临时文件和缓存文件。以下是代码。 import os import shutil def clean_folder(folder_path): for root,…...

2024年【天津市安全员C证】免费试题及天津市安全员C证试题及解析
题库来源:安全生产模拟考试一点通公众号小程序 天津市安全员C证免费试题是安全生产模拟考试一点通生成的,天津市安全员C证证模拟考试题库是根据天津市安全员C证最新版教材汇编出天津市安全员C证仿真模拟考试。2024年【天津市安全员C证】免费试题及天津市…...
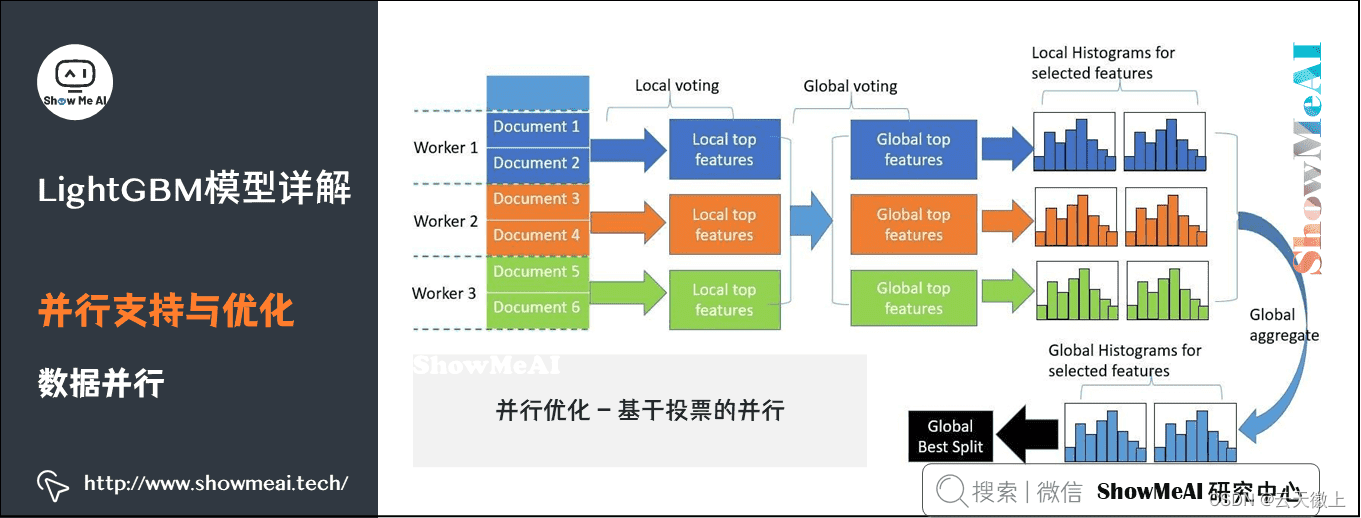
【Python数据挖掘实战案例】机器学习LightGBM算法原理、特点、应用---基于鸢尾花iris数据集分类实战
一、引言 1、简要介绍数据挖掘的重要性和应用 在数字化时代,数据已经成为企业和社会决策的重要依据。数据挖掘作为一门交叉学科,结合了统计学、机器学习、数据库技术和可视化等多个领域的知识,旨在从海量数据中提取有价值的信息,…...
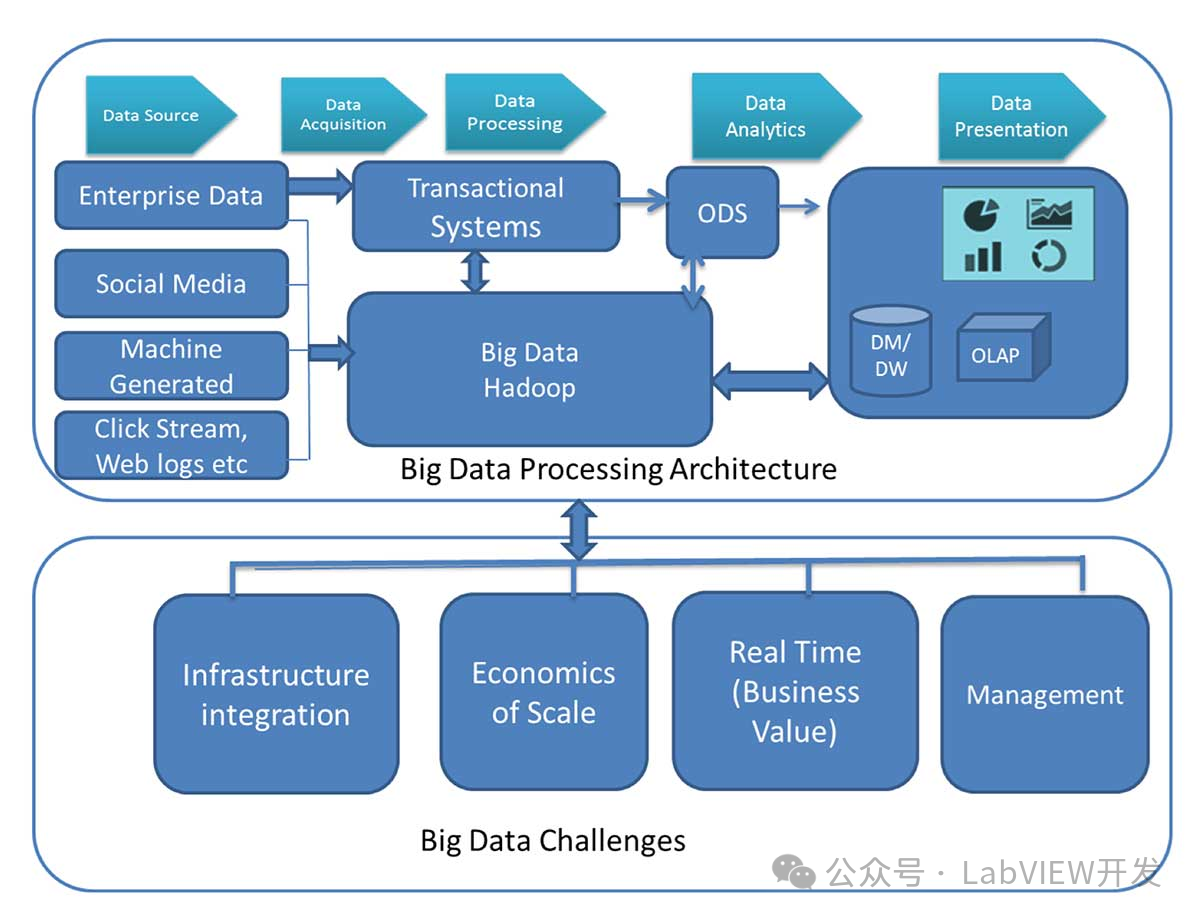
使用LabVIEW进行大数据数组操作的优化方法
针对大数据量数组操作,传统的内存处理方法可能导致内存不足。通过LabVIEW的图像批处理技术,可以有效地进行大数据数组操作,包括分块处理、并行处理和内存优化等。这种方法能显著提高处理效率和系统稳定性。 图像批处理的优势 内存优化&#…...
【Linux】(五)—— SSH远程登录和XShell使用
SSH Linux中的SSH(Secure Shell)是一个强大的网络协议,用于在不安全的网络环境中提供安全的远程登录和资料拷贝等其他网络服务。以下是有关Linux中SSH的关键点和操作指南: SSH的基础概念 安全性:SSH通过对所有传输的…...

前端怎么实现跨域请求?
前端实现跨域请求(Cross-Origin Resource Sharing, CORS)通常涉及到后端服务器的配置,因为浏览器的同源策略(Same-Origin Policy)会阻止前端代码直接发起跨域请求。然而,有几种方法可以在前端和后端的配合下…...

sqlmap直接嗦 dnslog注入 sqllibs第8关
dnslog注入是解决注入的时候没有回显的情况,通过dns外带来进行得到我们想要的数据。 我们是用了dns解析的时候会留下记录,这时候就可以看见我们想要的内容。 这个时候我们还要了解unc路径以及一个函数load_file()以及concat来进行注入。看看我的笔记 unc…...

数据结构笔记 3 串 数组 广义表
以下了解即可,暂时没发现有什么考点 参考: 【数据结构】——多维数组和广义表_数据结构loc-CSDN博客 相对应的题目: 他这个数组不是从0开始的,是从1开始的,所以为了配合公式要减1 下面这道题又不一样,它是…...
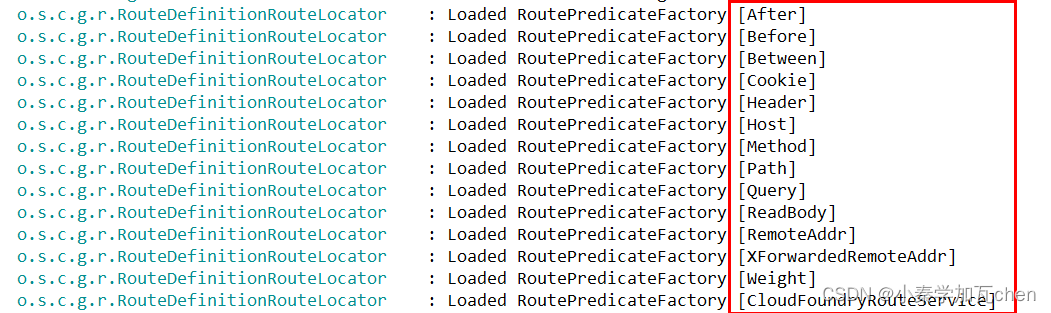
SpringCloud微服务GateWay网关使用与配置
一、概念 1、什么是GateWay网关 在微服务架构中,Gateway(网关)是一个重要的组件,负责处理外部请求并将它们路由到适当的微服务。以下是Gateway在微服务中的一些主要功能: 路由: Gateway负责将来自客户端的…...

win7补丁下载
目的 一般来说,安装上windows系统就带着补丁了,但有时,安装的是原始版的操作系统是不带补丁的,一般直接更新就可以了,但有时,电脑不能联网,只能通过安装包进行升级,所以下面介绍如何…...

在Cisco Packet Tracer上配置NAT
目录 前言一、搭建网络拓扑1.1 配置PC机1.2 配置客户路由器1.3 配置ISP路由器 二、配置NAT2.1 在客户路由器中配置NAT2.2 测试是否配置成功 总结 前言 本篇文章是在了解NAT的原理基础上,通过使用Cisco Packet Tracer 网络模拟器实现模拟对NAT的配置,以加…...

Web前端工程师的前景:挑战与机遇并存
Web前端工程师的前景:挑战与机遇并存 随着互联网的飞速发展和数字化转型的深入推进,Web前端工程师的前景日益广阔且充满挑战。作为互联网技术的核心力量之一,前端工程师的角色越来越重要,但同时也面临着技术更新迅速、市场需求多…...
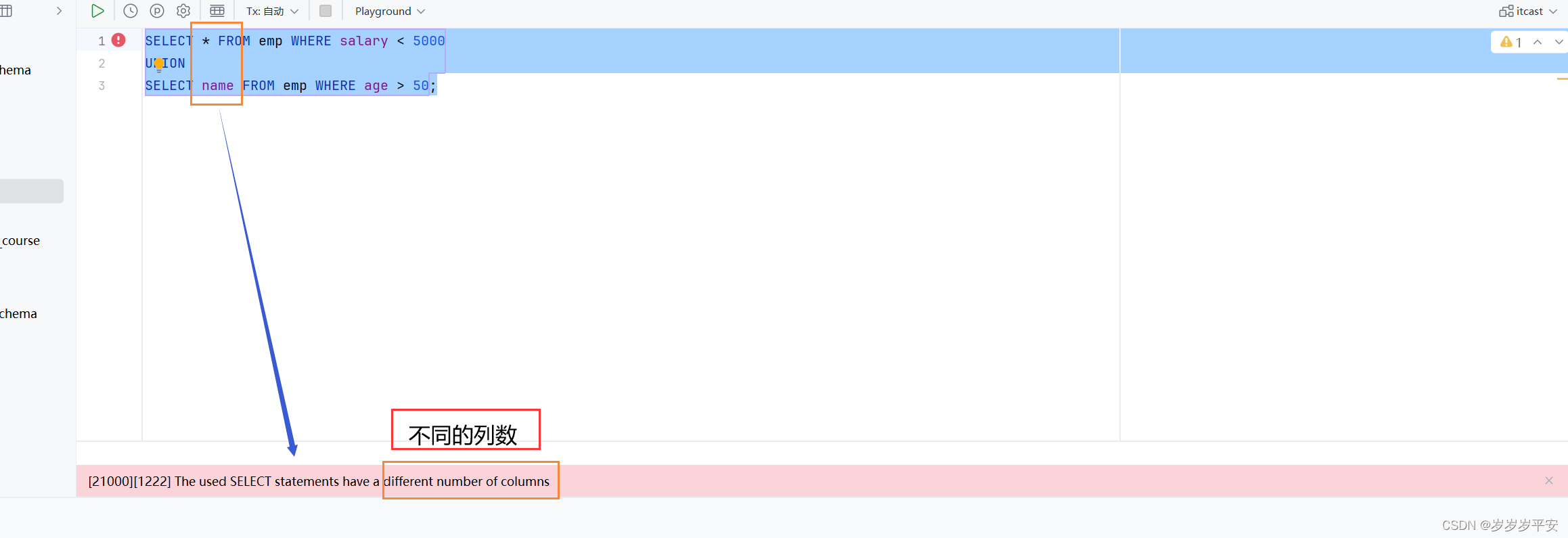
MySQL—多表查询—联合查询
一、引言 之前学习了连接查询。现在学习联合查询。 union:联合、联盟 对于union查询,就是把多次查询的结果合并起来,形成一个新的查询结果集 涉及到两个关键字:union 和 union all 注意: union 会把上面两个SQL查询…...

2024 Jiangsu Collegiate Programming Contest E. Divide 题解 主席树
Divide 题目描述 Given an integer sequence a 1 , a 2 , … , a n a_1,a_2,\ldots,a_n a1,a2,…,an of length n n n. For an interval a l , … , a r a_l,\ldots,a_r al,…,ar in this sequence, a Reduce operation divides the maximum value of the inter…...
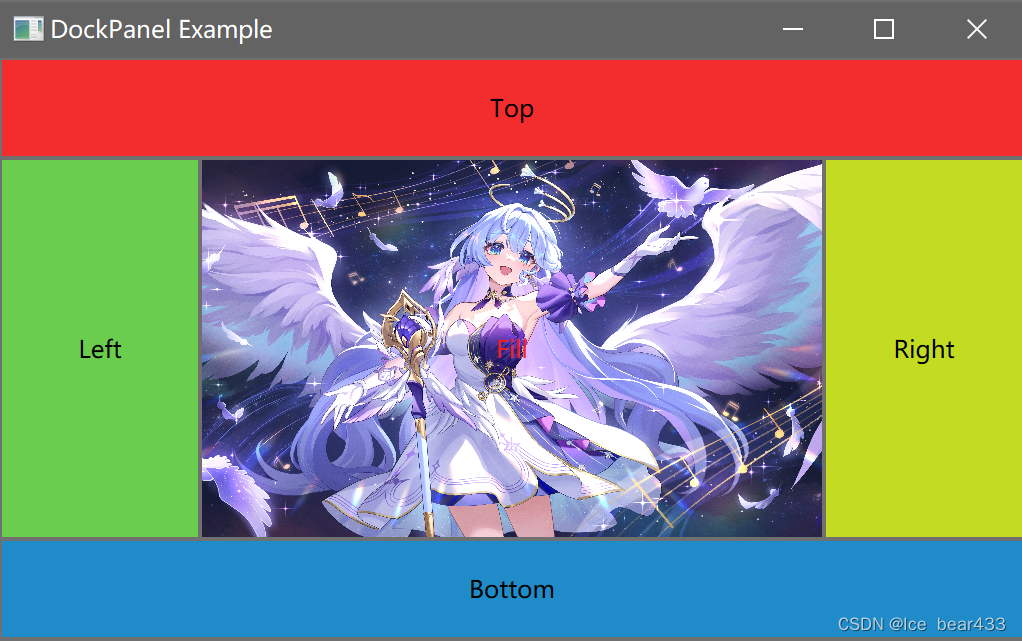
C# WPF入门学习主线篇(十五)—— DockPanel布局容器
C# WPF入门学习主线篇(十五)—— DockPanel布局容器 欢迎来到C# WPF入门学习系列的第十五篇。在前几篇文章中,我们探讨了 Canvas、StackPanel 和 WrapPanel 布局容器及其使用方法。本篇博客将介绍另一种强大且常用的布局容器——DockPanel。…...

基于SVPWM矢量控制的无速度传感器电机控制系统simulink建模与仿真
目录 1.课题概述 2.系统仿真结果 3.核心程序与模型 4.系统原理简介 5.完整工程文件 1.课题概述 基于SVPWM矢量控制的无速度传感器电机控制系统simulink建模与仿真,包括电机,SVPWM模块,矢量控制器模块等。 2.系统仿真结果 3.核心程序与模…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...
