AIGC作答《2024年高考作文|新课标I卷》能拿多少分?
AIGC作答《2024年高考作文|新课标I卷》能拿多少分?
- 一、前言
- 二、题目
- 三、作答
一、前言
如火如荼的2024年高考圆满落幕,在如此Happy的时刻,AIGC技术正以其前所未有的热度席卷全球。它不仅改变了我们获取信息的方式,也重塑了内容创作的边界。接下来,将借助这一前沿技术,尝试以AIGC为笔,书写一篇高考作文,探索人工智能与人类智慧的完美融合。

二、题目
2024年高考作文|新课标I卷作文题目
试题内容:阅读下面的材料,根据要求写作。(60分)
随着互联网的普及、人工智能的应用,越来越多的问题能很快得到答案。那么,我们的问题是否会越来越少?
以上材料引发了你怎样的联想和思考?请写一篇文章。
要求:选准角度,确定立意,明确文体,自拟标题;不要套作,不得抄袭;不得泄露个人信息;不少于800字。
三、作答
如下出自于某GPT的第一次作答。
随着互联网的普及和人工智能技术的飞速发展,我们正处在一个信息爆炸的时代。在这个背景下,越来越多的问题似乎都能迅速得到解答,这不禁引发了人们的思考:我们的问题真的越来越少了吗?
首先,我们需要认识到,问题的减少并非是因为问题本身在减少,而是因为获取答案的途径变得更加便捷。互联网和人工智能为我们提供了一个巨大的知识库,使得我们可以快速地检索到所需的信息。然而,这种便捷性也带来了一些负面影响。人们可能变得过于依赖搜索引擎和智能助手,逐渐丧失了独立思考和深入探究问题的能力。
其次,问题的减少也可能是因为我们在面对问题时,往往只满足于表面的答案,而忽视了问题的深层次含义。**在信息泛滥的时代,我们容易被各种信息所淹没,从而缺乏对问题的深入挖掘和思考。**这不仅限制了我们的认知深度,也可能导致我们错过一些重要的发现和创新。
然而,问题的本质并没有因为技术的发展而改变。问题始终是推动人类社会进步的重要动力。在人工智能的帮助下,我们应该更加积极地去寻找问题,而不是等待问题的出现。我们应该利用技术的优势,去探索未知的领域,去解决那些看似无法解决的问题。
此外,我们还应该培养自己的批判性思维能力。**在面对海量信息时,我们需要学会筛选、分析和评估信息的可靠性和价值。**只有这样,我们才能在信息的海洋中找到真正的宝藏,提出真正有价值的问题。
最后,我们应该意识到,问题的多少并不是衡量一个社会进步的唯一标准。更重要的是,我们如何面对问题,如何解决问题。在人工智能的帮助下,我们应该更加自信地面对挑战,更加勇敢地探索未知,从而推动人类社会不断向前发展。
总之,互联网和人工智能为我们提供了前所未有的便利,但它们并不是问题减少的原因。相反,我们应该利用这些技术,去发现更多的问题,去探索更广阔的世界。在这个过程中,我们的问题不仅不会减少,反而会变得更加丰富和深刻。
这篇作文似乎字数不足800,能拿多少分?
相关文章:

AIGC作答《2024年高考作文|新课标I卷》能拿多少分?
AIGC作答《2024年高考作文|新课标I卷》能拿多少分? 一、前言二、题目三、作答 一、前言 如火如荼的2024年高考圆满落幕,在如此Happy的时刻,AIGC技术正以其前所未有的热度席卷全球。它不仅改变了我们获取信息的方式,也…...

WHAT - 发布订阅
目录 一、常见实现方案1.1 使用事件发射器(Event Emitter)1.2 自定义事件系统(EventBus)1.3 使用库如 PubSubJS1.4 使用框架内置的状态管理工具Vue.jsReact (使用 Context API 或 Redux) 二、先后关系2.1 缓存事件数据2.2 使用 Re…...
useEffect)
React@16.x(23)useEffect
目录 1,介绍作用介绍 2,注意点2.1,参数1,副作用函数2.1.1,运行时间点2.1.2,返回值2.1.3,闭包的影响2.1.4,严禁出现在代码块中(判断,循环)2.1.5&am…...

算法竞赛一句话解题经典问题分析 ©ntsc 2024
原名:算法竞赛一句话解题&经典问题分析 ©ntsc 2024 处理进度 绿:P1381【~P(今日进度)】蓝:P1099 致CSDN网友: 本文章不定期更新!文章链接: 经典问题分析 基础知识与编程…...

【TensorFlow深度学习】强化学习中的贝尔曼方程及其应用
强化学习中的贝尔曼方程及其应用 强化学习中的贝尔曼方程及其应用:理解与实战演练贝尔曼方程简介应用场景代码实例:使用Python实现贝尔曼方程求解状态价值结语 强化学习中的贝尔曼方程及其应用:理解与实战演练 在强化学习这一复杂而迷人的领…...

牛客 NC129 阶乘末尾0的数量【简单 基础数学 Java/Go/PHP/C++】
题目 题目链接: https://www.nowcoder.com/practice/aa03dff18376454c9d2e359163bf44b8 https://www.lintcode.com/problem/2 思路 Java代码 import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改ÿ…...

【Spring Boot】异常处理
异常处理 1.认识异常处理1.1 异常处理的必要性1.2 异常的分类1.3 如何处理异常1.3.1 捕获异常1.3.2 抛出异常1.3.4 自定义异常 1.4 Spring Boot 默认的异常处理 2.使用控制器通知3.自定义错误处理控制器3.1 自定义一个错误的处理控制器3.2 自定义业务异常类3.2.1 自定义异常类3…...

Laravel学习-自定义辅助函数
因为laravel框架的辅助函数helpers不会进入版本库,被版本库忽略的,只有自己创建一个helpers辅助函数。 可以在任意文件下创建helpers.php文件,建议在app目录下, 然后在composer.json文件中,autoload 中间,…...

LLVM Cpu0 新后端6
想好好熟悉一下llvm开发一个新后端都要干什么,于是参考了老师的系列文章: LLVM 后端实践笔记 代码在这里(还没来得及准备,先用网盘暂存一下): 链接: https://pan.baidu.com/s/1yLAtXs9XwtyEzYSlDCSlqw?…...
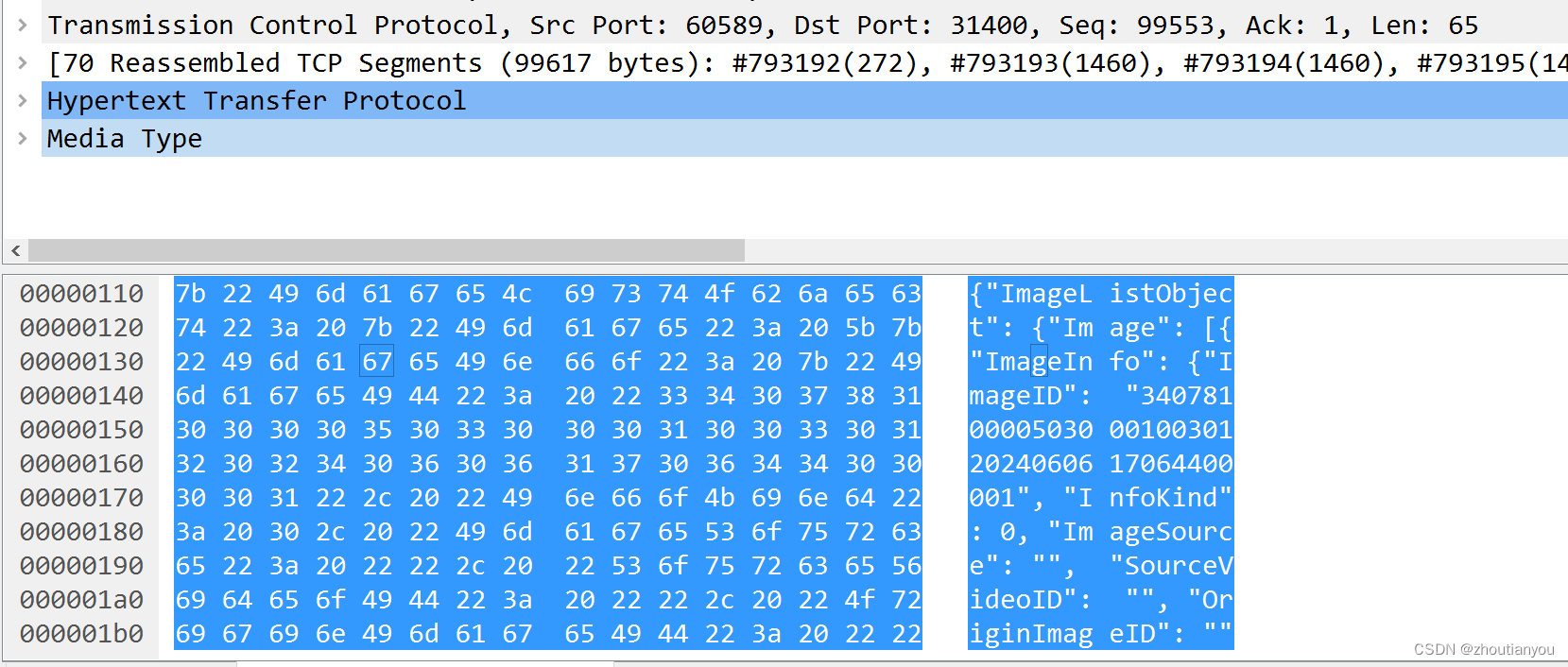
GAT1399协议分析(9)--图像上传
一、官方定义 二、wirechark实例 有前面查询的基础,这个接口相对简单很多。 请求: 文本化: POST /VIID/Images HTTP/1.1 Host: 10.0.201.56:31400 User-Agent: python-requests/2.32.3 Accept-Encoding: gzip, deflate Accept: */* Connection: keep-alive content-type:…...

Spring ApplicationContext的getBean方法
Spring ApplicationContext的getBean方法 在Spring框架的ApplicationContext中,getBean(Class<T> requiredType)方法可以接受一个类类型参数,这个参数可以是接口类也可以是实现类。 使用接口类: 如果requiredType是一个接口,…...
—— 自动摘要)
自然语言处理(NLP)—— 自动摘要
自动摘要是一种将长文本信息浓缩为短文本的技术,旨在保留原文的主要信息和意义。 1 自动摘要的第一种方法 它的第一种方法是基于理解的,受认知科学和人工智能的启发。 在这个方法中,我们首先建立文本的语义表示,这可以理解为文本…...

Spring RestClient报错:400 Bad Request : [no body]
我项目采用微服务架构,所以各服务之间通过Spring RestClient远程调用,本来一直工作得好好的,昨天突然发现远程调用一直报错,错误详情如下: org.springframework.web.client.HttpClientErrorException$BadRequest: 400…...
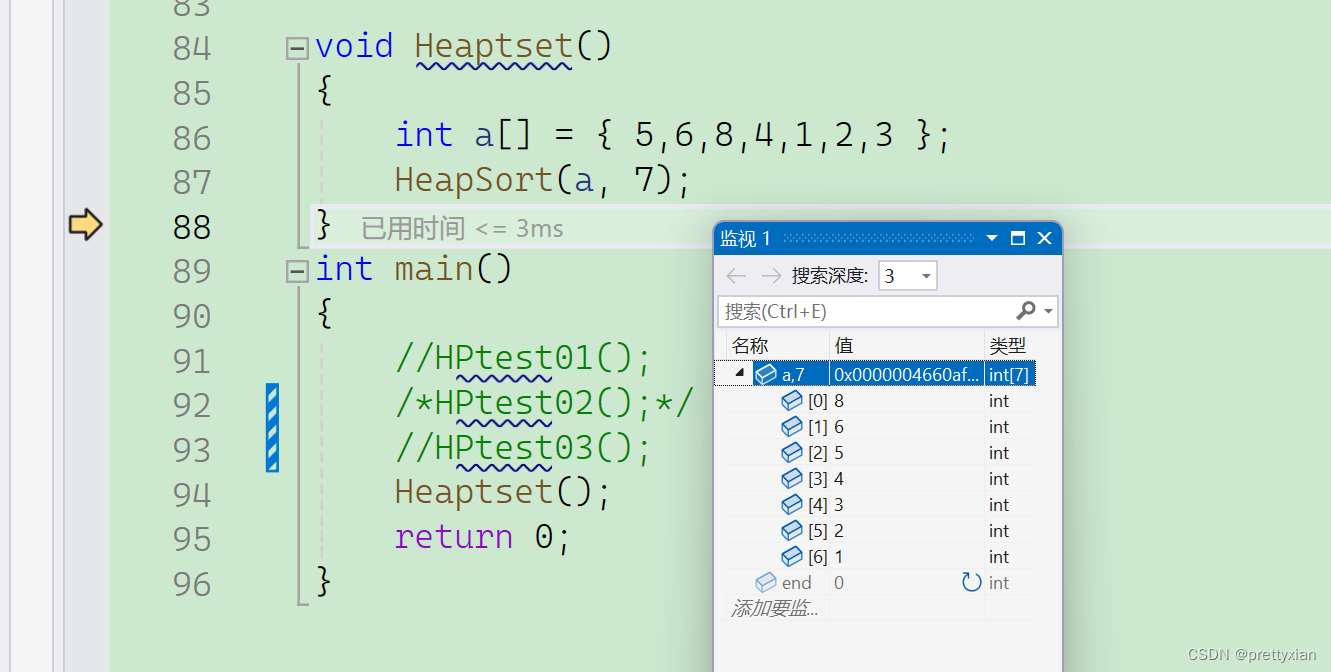
【数据结构】 -- 堆 (堆排序)(TOP-K问题)
引入 要学习堆,首先要先简单的了解一下二叉树,二叉树是一种常见的树形数据结构,每个节点最多有两个子节点,通常称为左子节点和右子节点。它具有以下特点: 根节点(Root):树的顶部节…...

C#面:XML与 HTML 的主要区别是什么
C# XML与HTML有以下几个主要区别: 用途不同:XML(eXtensible Markup Language)是一种用于存储和传输数据的标记语言,它的主要目的是描述数据的结构和内容。HTML(HyperText Markup Language)是一…...

java并发-如何保证线程按照顺序执行?
【readme】 使用只有单个线程的线程池(最简单)Thread.join() 可重入锁 ReentrantLock Condition 条件变量(多个) ; 原理如下: 任务1执行前在锁1上阻塞;执行完成后在锁2上唤醒;任务…...

PyCharm中 Fitten Code插件的使用说明一
一. 简介 Fitten Code插件是是一款由非十大模型驱动的 AI 编程助手,它可以自动生成代码,提升开发效率,帮您调试 Bug,节省您的时间,另外还可以对话聊天,解决您编程碰到的问题。 前一篇文章学习了 PyCharm…...
Polar Web【简单】PHP反序列化初试
Polar Web【简单】PHP反序列化初试 Contents Polar Web【简单】PHP反序列化初试思路EXP手动脚本PythonGo 运行&总结 思路 启动环境,显示下图中的PHP代码,于是展开分析: 首先发现Easy类中有魔术函数 __wakeup() ,实现的是对成员…...
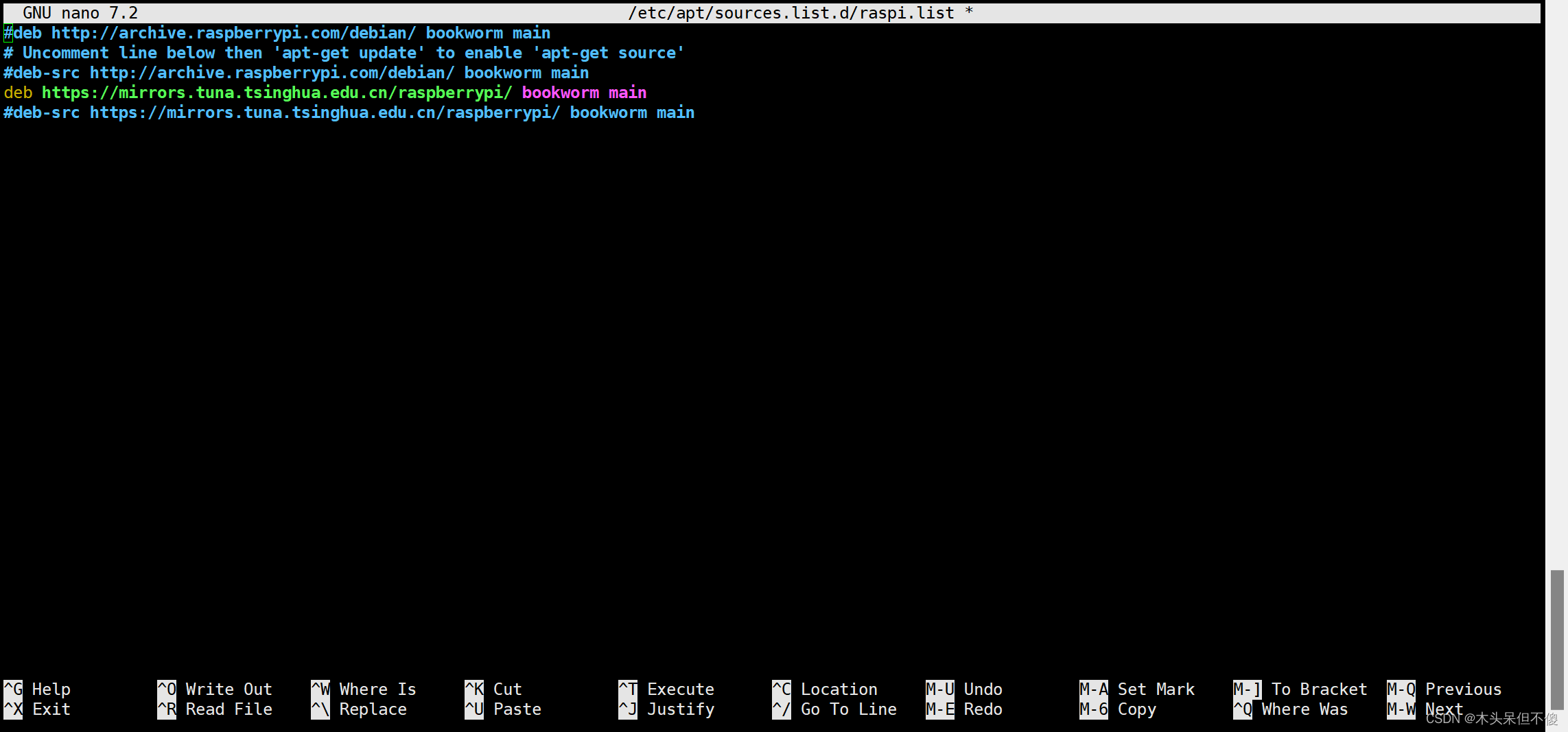
树莓派4B 零起点(二) 树莓派 更换软件源和软件仓库
目录 一、准备工作,查看自己的树莓派版本 二、安装HTTPS支持 三、更换为清华源 1、更换Debian软件源 2,更换Raspberrypi软件仓库 四、进行软件更新 接前章,我们的树莓派已经启动起来了,接下来要干的事那就是更换软件源和软件…...
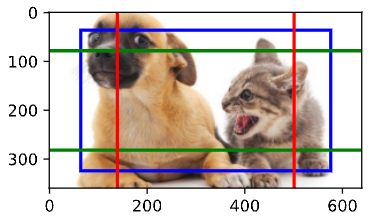
Pytorch 实现目标检测二(Pytorch 24)
一 实例操作目标检测 下面通过一个具体的例子来说明锚框标签。我们已经为加载图像中的狗和猫定义了真实边界框,其中第一个 元素是类别(0代表狗,1代表猫),其余四个元素是左上角和右下角的(x, y)轴坐标(范围…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...
