lua中大数相乘的问题
math.maxinteger * 2 --> -2
原因:math.maxinteger的二进制 :
0111111111111111111111111111111111111111111111111111111111111111
往左移位,最右加一个0,是
1111111111111111111111111111111111111111111111111111111111111110
对应的十六进制机器位 0xFFFFFFFFFFFFFFFE 对应的真值也就是-2
math.mininteger * 2 --> 0
对应二进制:
1000000000000000000000000000000000000000000000000000000000000000
乘二后的二进制:
0000000000000000000000000000000000000000000000000000000000000000
显然是0
math.maxinteger * math.maxinteger
同样采用移位的思路分析,已知maxinteger是奇数,那么就是math.maxinteger的二进制移位n次后再加一个数m,首先确定n是多少,math.maxinteger 是2^63+(-1),n是63, 之后确定m,m=-1
先把math.maxinteger 左移 63位,为:
1000000000000000000000000000000000000000000000000000000000000000
对应真值 mininteger (也就是-2^64)
再加上-math.maxinteger(二进制
1000000000000000000000000000000000000000000000000000000000000001
),
1000000000000000000000000000000000000000000000000000000000000000
+
1000000000000000000000000000000000000000000000000000000000000001
结果是:
0000000000000000000000000000000000000000000000000000000000000001
显然真值为1
math.mininteger * math.mininteger --> 0
可以从补码乘法的角度理解,具体参考补码乘法。
https://web.archive.org/web/20150213203512/http://pages.cs.wisc.edu/~cs354-1/beyond354/int.mult.html
方便起见,以4位计算机为例:(有符号整数范围-8到7)
11111000 -8x 11111000 x -8---------------- ------00000000 00000000000000001111100011111000111110001111100011111000----------------111000001000000
截断后四位,真值是0, 同理,math.mininteger * math.mininteger的结果也是0
值得一提的是,如果观察后8位,同样能得出64的正确真值,而这个数对16取模依然是0(等效于溢出后的运算结果)
相关文章:

lua中大数相乘的问题
math.maxinteger * 2 --> -2 原因:math.maxinteger的二进制 : 0111111111111111111111111111111111111111111111111111111111111111 往左移位,最右加一个0,是 1111111111111111111111111111111111111111111111111111111111111…...
第一个SpringBoot项目
目录 💭1、新建New Project IDEA2023版本创建Sping项目只能勾选17和21,却无法使用Java8?🌟 2、下载JDK 17🌟 💭2、项目创建成功界面 1、目录 🌟 2、pom文件🌟 💭3、…...

Android 10.0 Launcher修改density禁止布局改变功能实现
1.前言 在10.0的系统rom定制化开发中,在关于Launcher3的定制化功能中,在有些功能需要要求改变系统原有的density屏幕密度, 这样就会造成Launcher3的布局变化,所以就不符合要求,接下来就来看下如何禁止改变density造成Launcher3布局功能 改变的实现 2.Launcher修改densit…...
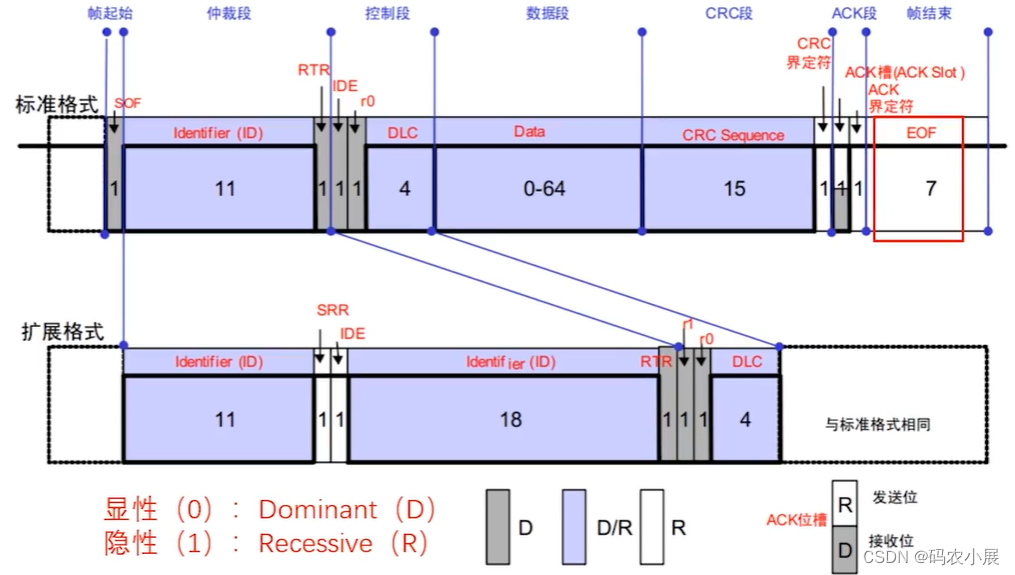
CAN协议简介
协议简介 can协议是一种用于控制网络的通信协议。它是一种基于广播的多主机总线网络协议,常用于工业自动化和控制领域。can协议具有高可靠性、实时性强和抗干扰能力强的特点,被广泛应用于汽车、机械、航空等领域。 can协议采用了先进的冲突检测和错误检测…...

(二)JSX基础
什么是JSX 概念:JSX是JavaScript和XML(HTML)的缩写,表示在JS代码中编写HTML模版结构,它是React中编写UI模板的方式。 优势:1.HTML的声明式模版方法;2.JS的可编程能力 JSX的本质 JSX并不是标准…...

GB 38469-2019 船舶涂料中有害物质限量检测
船舶涂料是指涂于船舶各部位,能防止海水、海洋大气腐蚀和海生物附着及满足船舶特种要求的各种涂料的统称。 GB 38469-2019船舶涂料中有害物质限量检测项目: 测试指标 测试方法 挥发性有机化合物VOC GB 30981 甲苯 GB 24408 苯 GB 30981 甲醇 G…...
汇编:数组-寻址取数据
比例因子寻址: 比例因子寻址(也称为比例缩放索引寻址或基址加变址加比例因子寻址)是一种复杂的内存寻址方式,常用于数组和指针操作。它允许通过一个基址寄存器、一个变址寄存器和一个比例因子来计算内存地址。 语法 比例因子寻…...

ROS自带的OpenCV库和自己安装版本冲突问题现象及解决方法
文章目录 1. 问题现象1.1 编译过程警告1.2 程序运行报错 2. 分析问题原因3. 解决方法 1. 问题现象 1.1 编译过程警告 warning: lipopencv_improc.so.406, needed by /usr/local/lib/libopencv_xfeatures2d.so.4.6.0, may conflict with libopencv_imgproc.so.4.21.2 程序运行…...

html+CSS+js部分基础运用19
1. 应用动态props传递数据,输出影片的图片、名称和描述等信息【要求使用props】,效果图如下: 2.在页面中定义一个按钮和一行文本,通过单击按钮实现放大文本的功能。【要求使用$emit()】 代码可以截图或者复制黏贴放置在“实验…...

探索 Debian 常用命令:掌握 Linux 系统管理的重要一步
Debian 作为一个稳定、高效和安全的操作系统,广泛应用于服务器、桌面和嵌入式系统中。对于新手和经验丰富的系统管理员来说,熟练掌握 Debian 的常用命令是管理和维护系统的基础。本文将详细介绍一些在 Debian 系统中经常使用的命令,帮助读者更好地理解和操作这个强大的操作系…...

「C系列」C 作用域规则
文章目录 一、C 作用域规则二、案例1. 块作用域(Block Scope)2. 文件作用域(File Scope)3. 静态作用域(Static Scope)静态局部变量静态全局变量 4. 函数参数的作用域5. 结构体和联合体的作用域 三、相关链接…...

【机器学习基础】Python编程10:五个实用练习题的解析与总结
Python是一种广泛使用的高级编程语言,它在机器学习领域中的重要性主要体现在以下几个方面: 简洁易学:Python语法简洁清晰,易于学习,使得初学者能够快速上手机器学习项目。 丰富的库支持:Python拥有大量的机…...

【设计模式】结构型设计模式之 门面模式
介绍 门面模式(Facade Pattern)是一种常用的设计模式,属于结构型模式的范畴。它为子系统中的一系列接口提供一个简化的统一接口,即一个外观(Facade),从而使子系统更加容易使用。门面模式并不修…...

MAC地址简介
一、MAC和ip地址 很多同学只知道ip地址,同时也知道ip在网络通讯中的重要性,实际上要实现网络通信的话,除了ip地址外还需要MAC地址的配合,只有在这两种地址的配合之下才能完整的实现互联网的通信。但是由于MAC地址的使用࿰…...

五种网络IO模型
目录 前言 文件描述符 为什么要多种io模型 同步IO 1.阻塞IO 2.非阻塞IO 3.多路复用IO(事件驱动IO) select: poll: epoll: 4.信号驱动IO 异步IO 区别 前言 文件描述符 首先我们了解一下文件描述符是什么:…...
VSCode超过390万下载的请求插件
Thunder Client 是一款在 VSCode(Visual Studio Code)中非常受欢迎的 REST API 客户端插件,由Ranga Vadhineni开发,现在已经有超过390万的下载量。它允许开发者直接在编辑器内发送 HTTP 请求,查看响应。Thunder Client…...

前端 JS 经典:下载的流式传输
触发下载在浏览器中有两种方式:1. 客户端的方式 2. 服务器的方式 1. 服务器的方式 通过 a 元素链接到一个服务器的地址,然后需要后端人员配置,当用户点击按钮请求这个地址时,服务端给他加上一个响应头。Content-Disposition 设置…...

k8s面试题大全,保姆级的攻略哦(三)
目录 1、简述ETCD及其特点? 2、简述ETCD适应的场景? 3、简述什么是Kubernetes? 4、简述Kubernetes和Docker的关系? 5、简述Kubernetes中什么是Minikube、Kubectl、Kubelet? 6、简述Kubernetes常见的部署方式? 7、简述Kubernetes如何实现集群管理? 8、简述Kubern…...

从年金理论到杠杆效应,再到财务报表与投资评估指标
一、解释普通年金终值和普通年金现值的概念。 普通年金终值:以利率为1%,每期收款100元,5期为例,普通年金终值的折算过程如图: 普通年金现值:以利率为1%,每期收款100元,5期为例&am…...
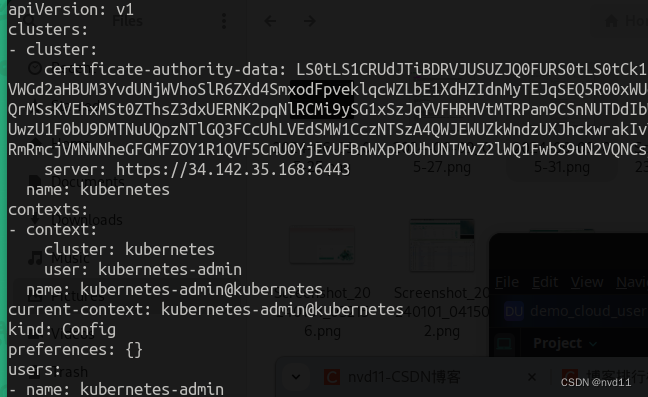
K8S - 用kubectl远程访问内网的k8s集群
在之前的文章 K8S - 在任意node里执行kubectl 命令 介绍过, 通过任何node 的主机, 用kubectl 管理集群是很简单 无非就是两个步骤: 下载 k8s master 上的admin.conf在当前主机配置 K8SCONFIG 环境变量指向 下载的config file 其他内网主机也适用 其…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
