从年金理论到杠杆效应,再到财务报表与投资评估指标
一、解释普通年金终值和普通年金现值的概念。
普通年金终值:以利率为1%,每期收款100元,5期为例,普通年金终值的折算过程如图:

普通年金现值:以利率为1%,每期收款100元,5期为例,普通年金现值的折算过程如图:

二、解释经营杠杆效应和财务杠杆效应,有相关文字和公式,以及推导过程。
-
经营杠杆(DOL)
经营杠杆:由于固定经营成本的存在,使得报酬的变动率大于业务量变动率的现象。从变动的传导来看,销量变动率——息税前利润变动率
含义:息税前利润变动率/业务量变动率,衡量经营风险。
提示:假设只有Q变化,导致了EBIT变化,右上角带了角标的表示下期,不带角标的表示基期,△表示变动额,其他数据各期保持不变。

如果固定成本为0,那么经营杠杆为1,经营风险最低。但是固定成本不可能为0,所以经营杠杆一般都是大于1的。 -
财务杠杆(DFL)
财务杠杆:由于固定性资本成本的存在,使得企业普通股收益变动率大于息税前利润变动率的现象。从变动的传导来看,息税前利润变动率——每股收益变动率
含义:每股收益变动率/息税前利润变动率,衡量财务风险

如果利息费用、优先股股利为0,那么财务杠杆为1,财务风险最低。对于大多数企业而言,存在利息费用,财务杠杆大于1。
三、零部件自制和购买分析,有哪几种情况?举例说明。
零部件自制或外购的决策分析一般可采用相关成本分析法和成本平衡点分析法。
-
零部件自制不需增加固定成本且自制能力无法转移
在企业已经具备的自制能力无法转移的情况下,原有的固定成本属于沉没成本,不会因零部件的自制或外购而发生变动。因此,在这项决策分析中,只需将自制方案的变动成本与外购成本进行比较。如果自制变动成本高于外购成本,应外购;如果自制变动成本低于外购成本,应自制。
【例】某企业每年需用A零件100 000件,该零件即可以自制,又可以外购。若外购每件单价为40元;若自制,企业拥有多余的生产能力且无法转移,其单位成本为:
直接材料30元
直接人工6元
变动制造费用3元
固定制造费用5元
单位成本合计44元
A零件是自制还是外购?
根据题意,可采用相关成本分析法。由于企业拥有多余的生产能力,固定成本属于无关成本,不需考虑,自制单位变动成本为39元(直接材料30元,直接人工6元,变动制造费用3元),外购单价为40元。有:
自制总成本为:100 000×39=3 900 000(元)
外购总成本为:100 000×40=4 000 000(元)
企业应选择自制方案,可节约成本100 000元。 -
零部件自制不需增加固定成本且自制能力可以转移
在自制能力可以转移的情况下,自制方案的相关成本除了包括按零部件全年需用量计算的变动生产成本外,还包括与自制能力转移有关的机会成本,无法通过直接比较单位变动生产成本与外购单价作出决策,必须采用相关成本分析法。
【例】仍依上例资料。假定自制A零件的生产能力可以转移,每年预计可以获得贡献毛益1 000 000元。A零件是自制还是外购?
根据题意,可采用相关成本分析法。由于企业拥有多余的生产能力,固定成本属于无关成本,不需考虑,自制单位变动成本为39元(直接材料30元,直接人工6元,变动制造费用3元),外购单价为40元。有:
自制A零件的机会成本为
依题意编制的相关损益分析表如表所示。

企业应选择外购方案,可节约成本900 000元。 -
零部件自制但需要增加固定成本
当自制零部件时,如果企业没有多余的生产能力或多余生产能力不足,就需要增加固定成本以购置必要的机器设备。在这种情况下,自制零部件的成本,就不仅包括变动成本,而且还包括增加的固定成本。由于单位固定成本是随产量成反比例变动的,因此对于不同的需要量,决策分析的结论就可能不同。这类问题的决策分析,根据零部件的需要量是否确定,可以分别采用相关成本分析法和成本平衡点分析法来进行分析。若零部件的需要量确定,可以采用相关成本分析法,若零部件的需要量不确定则采用成本平衡点分析法。因零部件的需要量确定情况下的零部件自制与否的决策与前例相似,这里仅就零部件需要量不确定情况下的自制与否的决策进行举例。
【例】企业需要的B零件可以外购,单价为60元;若自制单位变动成本为24元,每年还需增加固定成本45 000元。
要求:分析B零件是自制还是外购。
解:由于本例零部件的需要量不确定,因此需采用成本平衡点分析法进行分析。
设:x0为成本平衡点业务量,自制方案的总成本为y1,固定成本为a1,单位变动成本为b1;外购方案的总成本为y2,固定成本为a2,单位变动成本为b2。
其中:a1 = 45000元
b1 = 24元
a2 = 0
b2 = 60元
则有:y1 = a1 + b1x = 45000 + 24x
y2 = 60x
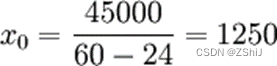 件
件
这说明,当零部件需要量在1 250件时,外购总成本与自制总成本相等;当零部件的需要量在1 250件以内时,外购总成本低于自制总成本,应选择外购方案;当零部件需要量超过1 250件时,自制总成本低于外购总成本,应选择自制方案。
四、解释资产负债表、利润表、现金流量表的内涵,分析它们的内在勾稽关系。
资产负债表、利润表和现金流量表具体科目之间也是相互关联的如下图所示:

三张报表的映射关系。

例子:

五、解释净现值、净现值率、现值指数的概念,引用公式和例子。
-
净现值(NPV)
含义:一个投资项目,其未来现金净流量现值与原始投资额现值之间的差额,称为净现值。
计算公式:净现值(NPV)=未来现金净流量现值-原始投资额现值
决策原则:
(1)净现值为正,方案可行,说明方案的实际收益率高于所要求的收益率;
(2)净现值为负,方案不可行,说明方案的实际投资收益率低于所要求的收益率;
(3)净现值为零,方案也可行,说明方案的投资收益刚好达到所要求的投资收益 -
净现值率
净现值率的经济含义:项目净现值与项目全部投资现值之比。反映单位投资现值所能带来的净现值。是净现值的辅助评价指标。适于多个投资额不同的项目方案的比选。
计算公式:NPVR= NPV/Ip
评价准则:(1)若NPVR≥0,说明投资方案在经济上可接受;(2)若NPVR<0,说明投资方案在经济上不可行。 -
现值指数(PVI)
含义:是指投资项目的未来现金净流量现值与原始投资额现值之比。
计算公式:现值指数(PVI)=未来现金净流量现值÷原始投资额现值
决策原则:(1)现值指数≥1,方案可行;(2)现值指数<1,方案不可行
相关文章:

从年金理论到杠杆效应,再到财务报表与投资评估指标
一、解释普通年金终值和普通年金现值的概念。 普通年金终值:以利率为1%,每期收款100元,5期为例,普通年金终值的折算过程如图: 普通年金现值:以利率为1%,每期收款100元,5期为例&am…...
K8S - 用kubectl远程访问内网的k8s集群
在之前的文章 K8S - 在任意node里执行kubectl 命令 介绍过, 通过任何node 的主机, 用kubectl 管理集群是很简单 无非就是两个步骤: 下载 k8s master 上的admin.conf在当前主机配置 K8SCONFIG 环境变量指向 下载的config file 其他内网主机也适用 其…...

STM32F103C8移植uCOSIII并以不同周期点亮两个LED灯(HAL库方式)【uCOS】【STM32开发板】【STM32CubeMX】
STM32F103C8移植uC/OSIII并以不同周期点亮两个LED灯(HAL库方式)【uC/OS】【STM32开发板】【STM32CubeMX】 实验说明 将嵌入式操作系统uC/OSIII移植到STM32F103C8上,构建两个任务,两个任务分别以1s和3s周期对LED进行点亮—熄灭的…...

【c语言】qsort函数及泛型冒泡排序的模拟实现
🌟🌟作者主页:ephemerals__ 🌟🌟所属专栏:C语言 目录 一、qsort函数 1.回调函数 2.qsort函数 3.void* 指针 二、泛型冒泡排序的模拟实现 1.比较函数的编写 2.交换函数的编写 3.冒泡排序的编写 4…...
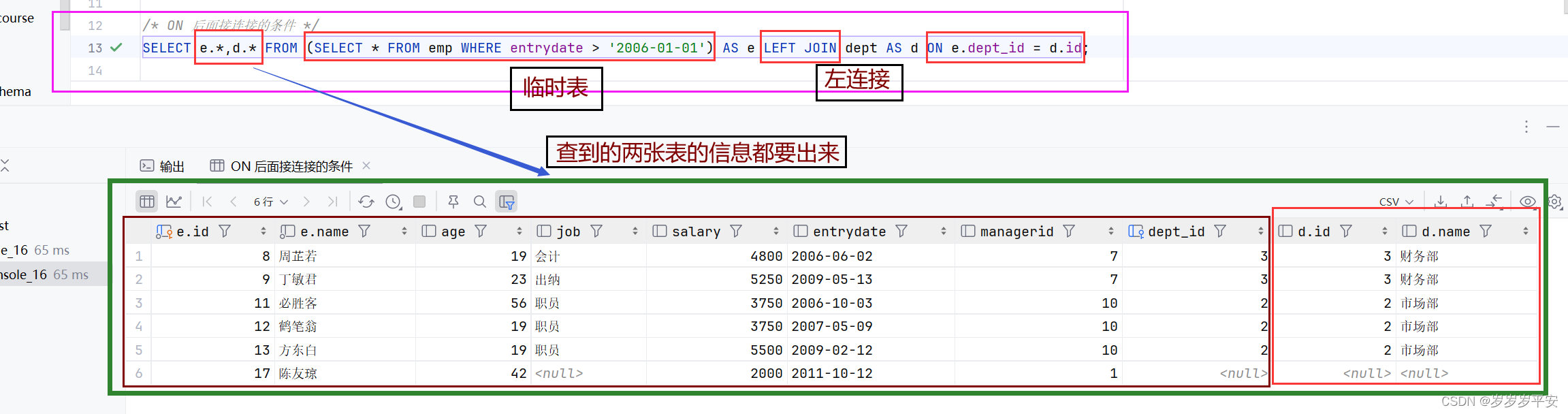
MySQL之多表查询—表子查询
一、引言 上一篇博客学习了行子查询。(看弹幕:同一张表用or,不同张表用union) 下面接着学习子查询当中的最后一种——表子查询。 表子查询 1、概念 子查询返回的结果是多行多列,这种子查询称为表子查询。 2、常用的操作符 IN 3、…...

Java 18风暴来袭:解锁编程新纪元
一、引言 Java 18的发布标志着Java语言在性能、安全性和开发效率方面的又一次飞跃。本次更新不仅带来了新的语言特性,还包括了一些实验性功能和工具的改进。这些新特性旨在帮助开发者编写更高效、更安全的代码,并提升开发体验。 二、新特性概述 1. 默…...

文件操作(Python和C++版)
一、C版 程序运行时产生的数据都属于临时数据,程序—旦运行结束都会被释放通过文件可以将数据持久化 C中对文件操作需要包含头文件< fstream > 文件类型分为两种: 1. 文本文件 - 文件以文本的ASCII码形式存储在计算机中 2. 二进制文件- 文件以文本的二进…...
Git【版本控制命令】
02 【本地库操作】 1.git的结构 2.Git 远程库——代码托管中心 2.1 git工作流程 代码托管中心用于维护 Git 的远程库。包括在局域网环境下搭建的 GitLab 服务器,以及在外网环境下的 GitHub 和 Gitee (码云)。 一般工作流程如下: 1.从远程…...
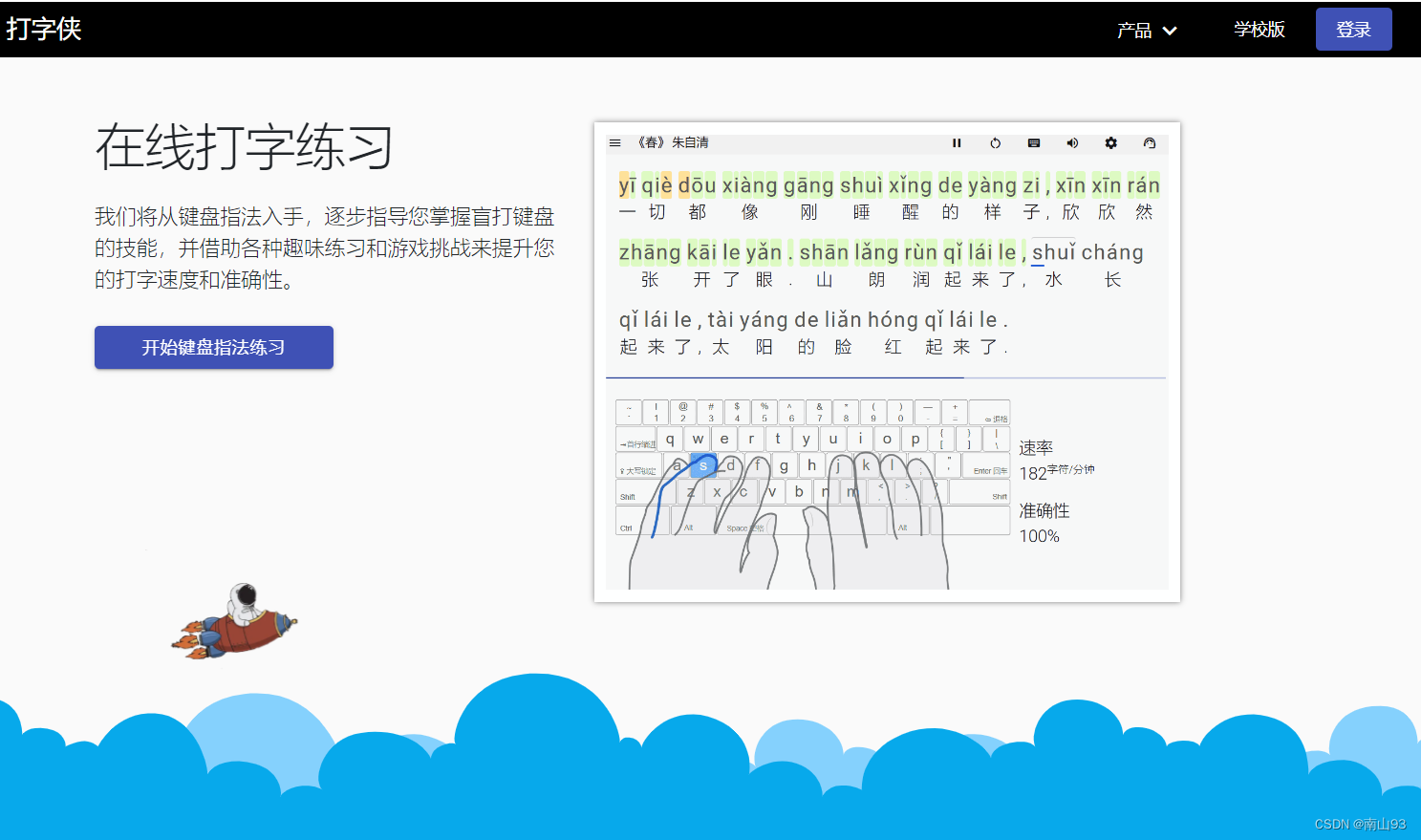
打字侠是一款PWA网站,如何下载到电脑桌面?
嘿,亲爱的键盘侠们! 你是否还在为寻找一款好用的打字练习工具而烦恼?别担心,今天我要给大家介绍一位超级英雄——打字侠!它不仅是一个超级酷的打字练习网站,还是一款PWA(渐进式网页应用&#x…...

Scikit-learn使用步骤?使用场景?
Scikit-learn(简称sklearn)是Python中一个非常流行的机器学习库,它提供了广泛的机器学习算法和工具,用于数据分析、特征工程、模型训练、模型评估等任务。以下是一个关于sklearn的基础教程,内容将按照几个主要部分进行…...
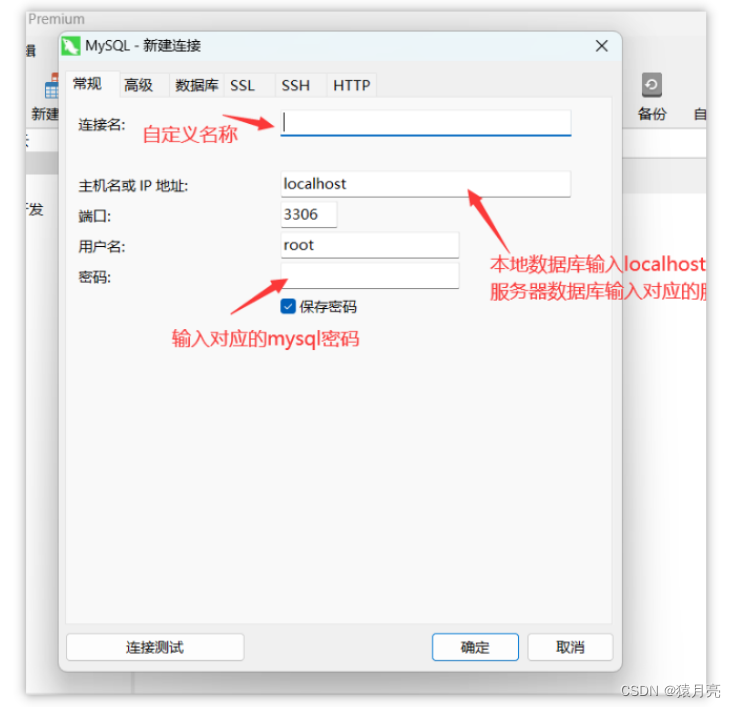
MySQL 5.7详细下载安装配置教程(MySQL 5.7安装包)_mysql5.7的安装教程
记录MySQL 5.7 的下载安装教程,并提供了Mysql 安装包 ,以下是详细下载安装过程。 一、下载Mysql安装包 网盘下载: 下载MySQL 5.7安装包,网盘下载地址:点击此处直接下载 官网下载: 进入官网,…...

电阻十大品牌供应商
选型时选择热门的电阻品牌,主要是产品丰富,需求基本都能满足。 所所有的电路中,基本没有不用电阻的,电阻的选型需要参考阻值、精度、封装、温度范围,贴片/插件等参数,优秀的供应商如下: 十大电…...
深度学习复盘与论文复现C
文章目录 4、Distributed training4.1 GPU architecture 5、Recurrent neural network5.1 The basic structure of RNN5.2 Neural networks without hidden states5.3 Recurrent neural networks with hidden states5.4 summary 6、Language Model Dataset (lyrics from Jay Ch…...

海洋日特别活动—深海来客——可燃冰
深海中有一种神奇的物质,似冰又不是冰。 别看它其貌不扬,但本领不小,遇火即燃,能量巨大,可谓是能源家族的新宠。它就是被国务院正式批准列为我国第173个矿种的“可燃冰”! 可燃冰到底是个啥?它…...

Web前端放图片位置:深入探索与最佳实践
Web前端放图片位置:深入探索与最佳实践 在Web前端开发中,图片作为重要的视觉元素,其放置位置往往影响着网页的整体布局和用户体验。然而,如何合理地放置图片,以最大化其视觉效果并提升用户体验,却是一个颇…...

leetcode-02-[977]有序数组的平方[209]长度最小的子数组[59]螺旋矩阵II
一、[977]有序数组的平方 重点: 新引入一个数组,不要原数组操作 class Solution {public int[] sortedSquares(int[] nums) {int left0,right nums.length-1;int[] resultnew int[nums.length];int index nums.length-1;while(left<right){if(nums…...

Spring Cloud Gateway CORS 跨域方案
通过配置文件,以下配置就是其中一种方案。 gateway: #跨域配置globalcors: cors-configurations: [/**]: allowedMethods: "*"allowedHeaders: "*"allowedOriginPatterns: "*"allowCredentials: truedefault-filters: - DedupeRespo…...

高考后志愿填报信息采集系统制作指南
在高考的硝烟散去之后,每位学生都面临着一个重要的任务——志愿填报。老师们如何高效、准确地收集和整理这些信息,成为了一个棘手的问题。难道我们只能依赖传统的手工登记方式,忍受其繁琐和易错吗? 易查分是一个简单易用的在线工具…...

Python使用Flask构建简单的web应用
构建一个简单的 Flask Web 应用程序是学习 Python Web 开发的良好起点。Flask 是一个轻量级的 WSGI Web 应用框架,它的主要目标是让开发者更容易构建 Web 应用,同时保持简单性和灵活性。下面我们将详细介绍如何使用 Flask 构建一个简单的 Web 应用&#…...

看似不同的事情,却是相同的坑
目录 一、背景二、过程1.遭遇战-微盘股的下杀2.不失为一件好事3.一切向后看吧,最近的学习感受4.该有的心境 三、总结 一、背景 也在一点点改变,期间势必要经历流血的过程;所谓无疯狂不成长,积极的心态去应对,去总结总…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...

python基础语法Ⅰ
python基础语法Ⅰ 常量和表达式变量是什么变量的语法1.定义变量使用变量 变量的类型1.整数2.浮点数(小数)3.字符串4.布尔5.其他 动态类型特征注释注释是什么注释的语法1.行注释2.文档字符串 注释的规范 常量和表达式 我们可以把python当作一个计算器,来进行一些算术…...

华为云Flexus+DeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手
华为云FlexusDeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手 一、构建知识库问答助手引言二、构建知识库问答助手环境2.1 基于FlexusX实例的Dify平台2.2 基于MaaS的模型API商用服务 三、构建知识库问答助手实战3.1 配置Dify环境3.2 创建知识库问答助手3.3 使用知…...

ABB馈线保护 REJ601 BD446NN1XG
配电网基本量程数字继电器 REJ601是一种专用馈线保护继电器,用于保护一次和二次配电网络中的公用事业和工业电力系统。该继电器在一个单元中提供了保护和监控功能的优化组合,具有同类产品中最佳的性能和可用性。 REJ601是一种专用馈线保护继电器…...
: 发布订阅模式)
JS设计模式(5): 发布订阅模式
解锁JavaScript发布订阅模式:让代码沟通更优雅 在JavaScript的世界里,我们常常会遇到这样的场景:多个模块之间需要相互通信,但是又不想让它们产生过于紧密的耦合。这时候,发布订阅模式就像一位优雅的信使,…...

HarmonyOS-ArkUI 自定义弹窗
自定义弹窗 自定义弹窗是界面开发中最为常用的一种弹窗写法。在自定义弹窗中, 布局样式完全由您决定,非常灵活。通常会被封装成工具类,以使得APP中所有弹窗具备相同的设计风格。 自定义弹窗具备的能力有 打开弹窗自定义布局,以…...

uniapp+<script setup lang=“ts“>解决有数据与暂无数据切换显示,有数据加载时暂无数据闪现(先加载空数据)问题
声明showEmpty 为false,在接口返回处判断有数据时设置showEmpty 为false,接口返回数据为空则判断showEmpty 为true (这样就解决有数据的时候会闪现暂无数据的问题啦) <!--* Date: 2024-02-26 03:38:52* LastEditTime: 2025-06…...
