leetcode-02-[977]有序数组的平方[209]长度最小的子数组[59]螺旋矩阵II
一、[977]有序数组的平方
重点:
新引入一个数组,不要原数组操作
class Solution {public int[] sortedSquares(int[] nums) {int left=0,right= nums.length-1;int[] result=new int[nums.length];int index= nums.length-1;while(left<=right){if(nums[left]*nums[left]>nums[right]*nums[right]){result[index]=nums[left]*nums[left];left++;}else{result[index]=nums[right]*nums[right];right--;}index--;}return result;}
}二、[209]长度最小的子数组
重点:
1、滑动窗口,for循环的 j 为终止位置
2、注意最后的处理,滑动窗口大小为0
class Solution {public int minSubArrayLen(int target, int[] nums) {//j为终止位置,i为起始位置int i=0,sum=0;int result=Integer.MAX_VALUE;for(int j=0;j< nums.length;j++){sum+=nums[j];//注意是while循环while(sum>=target){int tmp=j-i+1;result=Math.min(result, tmp);sum-=nums[i];i++;}}//没有满足条件的窗口则为0return result==Integer.MAX_VALUE?0:result;}
}三、[59]螺旋矩阵II
重点:
1、左闭右开
2、i 对应 X,j对应 Y
3、i为行,j为列 取自坐标(i,j)
class Solution {public int[][] generateMatrix(int n) {int[][] result=new int[n][n];int startX=0,startY=0;int loop=1;int offset=1;int count=1;int i=0,j=0;//左闭右开//i 对应 X,j对应 Y//i为行,j为列 取自坐标(i,j)while(loop<=n/2){for(j=startY;j<n-offset;j++){result[startX][j]=count++;}for(i=startX;i<n-offset;i++){result[i][j]=count++;}for(;j>startY;j--){result[i][j]=count++;}for(;i>startX;i--){result[i][j]=count++;}startX++;startY++;loop++;offset++;}if(n%2!=0){result[n/2][n/2]=count;}return result;}
}相关文章:

leetcode-02-[977]有序数组的平方[209]长度最小的子数组[59]螺旋矩阵II
一、[977]有序数组的平方 重点: 新引入一个数组,不要原数组操作 class Solution {public int[] sortedSquares(int[] nums) {int left0,right nums.length-1;int[] resultnew int[nums.length];int index nums.length-1;while(left<right){if(nums…...

Spring Cloud Gateway CORS 跨域方案
通过配置文件,以下配置就是其中一种方案。 gateway: #跨域配置globalcors: cors-configurations: [/**]: allowedMethods: "*"allowedHeaders: "*"allowedOriginPatterns: "*"allowCredentials: truedefault-filters: - DedupeRespo…...

高考后志愿填报信息采集系统制作指南
在高考的硝烟散去之后,每位学生都面临着一个重要的任务——志愿填报。老师们如何高效、准确地收集和整理这些信息,成为了一个棘手的问题。难道我们只能依赖传统的手工登记方式,忍受其繁琐和易错吗? 易查分是一个简单易用的在线工具…...

Python使用Flask构建简单的web应用
构建一个简单的 Flask Web 应用程序是学习 Python Web 开发的良好起点。Flask 是一个轻量级的 WSGI Web 应用框架,它的主要目标是让开发者更容易构建 Web 应用,同时保持简单性和灵活性。下面我们将详细介绍如何使用 Flask 构建一个简单的 Web 应用&#…...

看似不同的事情,却是相同的坑
目录 一、背景二、过程1.遭遇战-微盘股的下杀2.不失为一件好事3.一切向后看吧,最近的学习感受4.该有的心境 三、总结 一、背景 也在一点点改变,期间势必要经历流血的过程;所谓无疯狂不成长,积极的心态去应对,去总结总…...

在 Linux 系统上安装 Android NDK
在 Linux 系统上安装 Android NDK 1. Android NDK2. NDK Downloads2.1. Latest LTS Version (r26d)2.2. Old Unsupported Versions 3. 安装 NDK4. Get started with the NDK (NDK 使用入门)References 1. Android NDK https://developer.android.com/ndk The Android NDK is …...
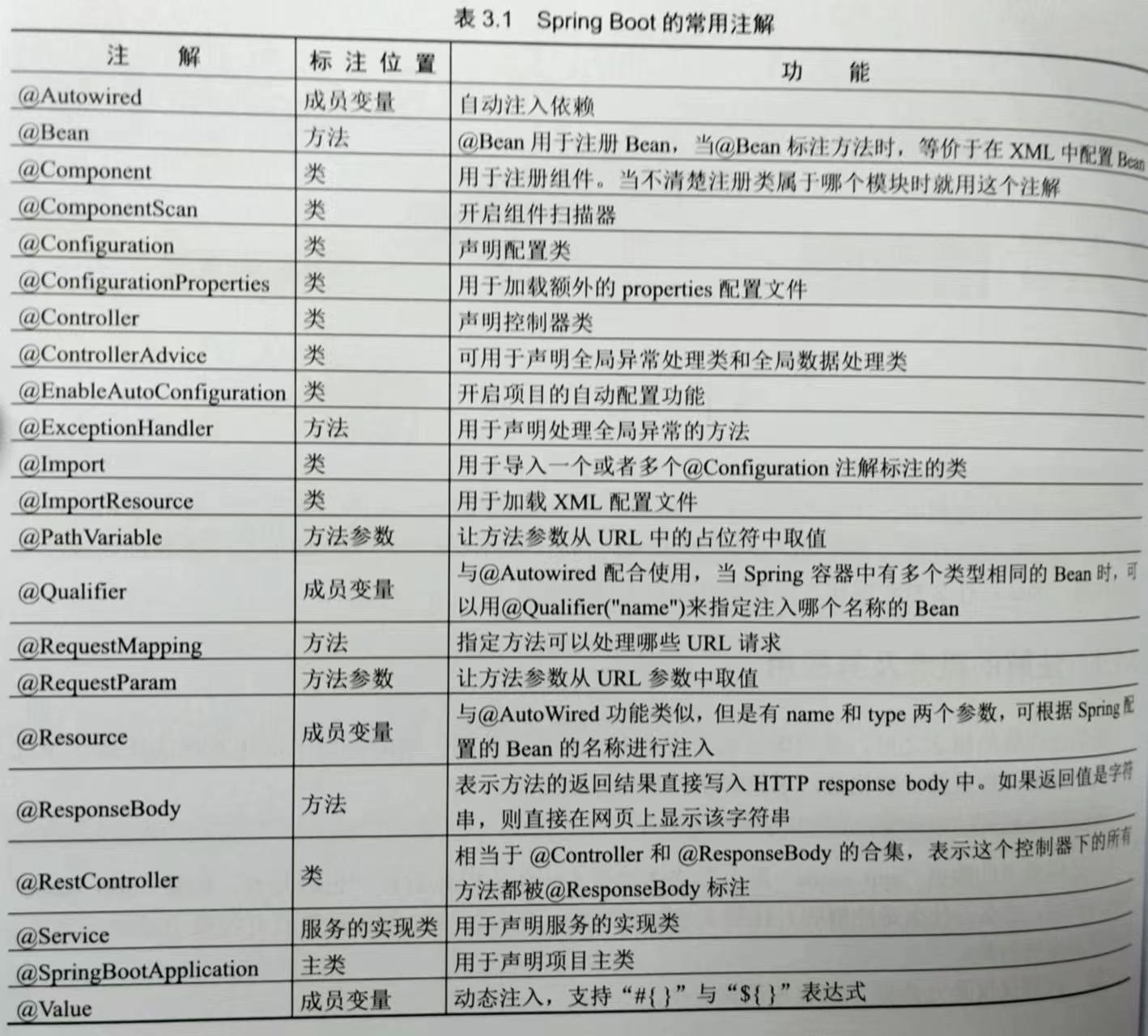
SpringBoot的学习要点
目录 SpringBoot 创建项目 配置文件 注解 命名规范 SpringBoot整合第三方技术 …… 中文文档:Spring Boot 中文文档 SpringBoot Spring Boot 是基于 Spring 框架的一种快速构建微服务应用的方式它主要提供了自动配置、简化配置、运行时应用监控等功能它…...

vue3引入cesium和olcs
首先引入包 pnpm i olcs; pnpm i -D vite-plugin-cesium pnpm i -S cesium在vite.config.js中配置,参考这位大佬的笔记 添加链接描述 import { defineConfig } from vite import vue from vitejs/plugin-vue import cesium from vite-plugin-cesium; // https://…...

代码随想录算法训练营第25天|回溯
回溯part02 216. 组合总和 III /*** param {number} k* param {number} n* return {number[][]}*/ var combinationSum3 function(k, n) {// k个数字相加为n// 只能使用1-9// 每个数字只能使用一次// 不能重复 如 1 2 4 、 4 1 2 不可以let res [];backtracking(k, n, [], …...
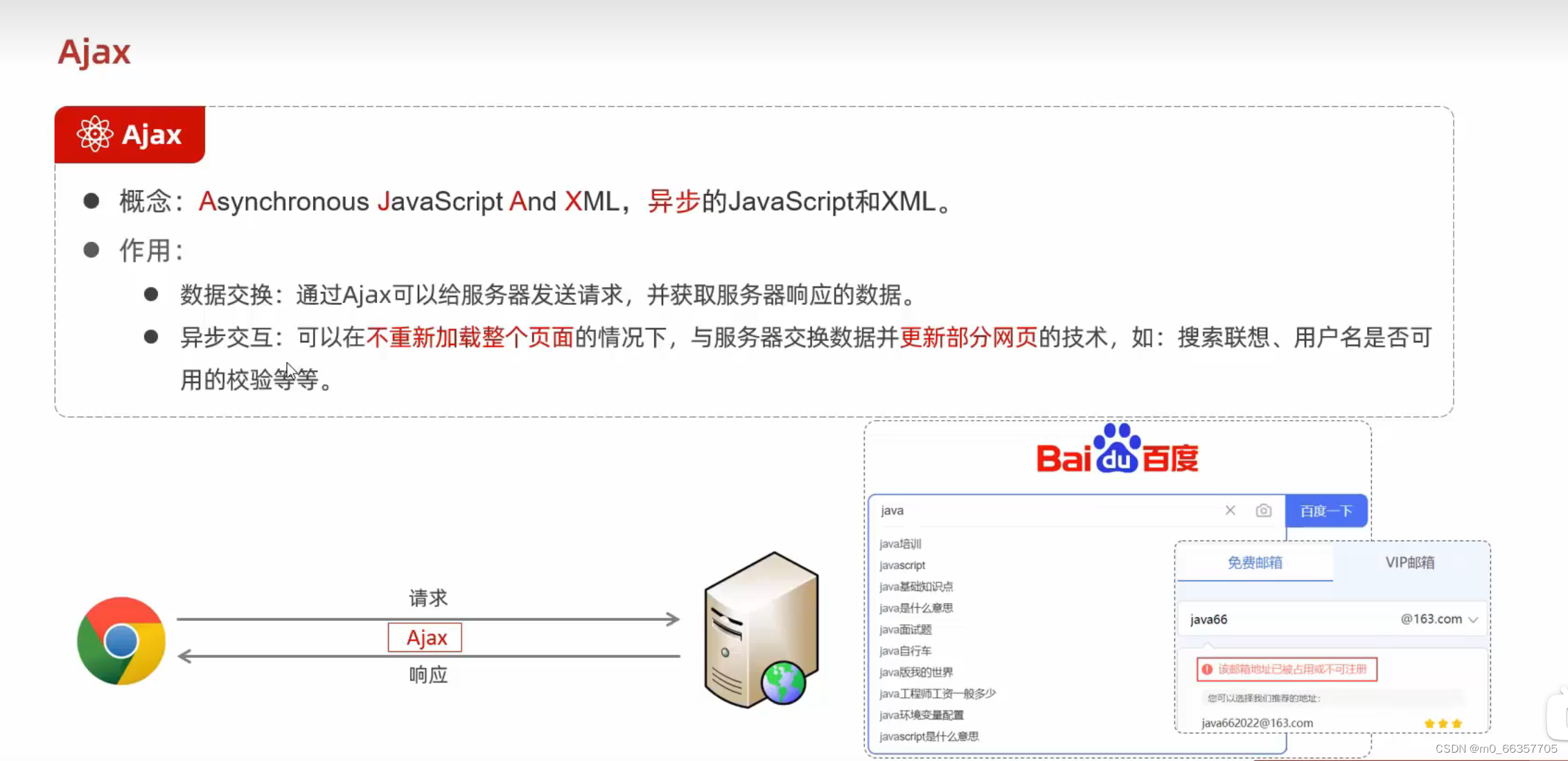
Ajax 快速入门
Ajax 概念:Ajax是一种Web开发技术,允许在不重新加载整个页面的情况下,与服务器交换数据并更新网页的部分内容。 作用: 数据交换:Ajax允许通过JavaScript向服务器发送请求,并能够接收服务器响应的数据。 异…...

面试官:前端实现图片懒加载怎么做?这不是撞我怀里了嘛!
前端懒加载(也称为延迟加载或按需加载)是一种网页性能优化的技术,主要用于在网页中延迟加载某些资源,如图片、视频或其他媒体文件,直到它们实际需要被用户查看或交互时才进行加载。这种技术特别适用于长页面或包含大量…...

每天学习一个Windows命令或Linux命令——seq
今天我们来学习 seq命令! seq命令(单词sequence序列的缩写)是Linux系统中用于输出序列化的一串整数的命令。 一、seq用法 seq用法一共有以下三种: seq [选项]... 尾数 seq [选项]... 首数 尾数 seq [选项]... 首数 增量&#…...
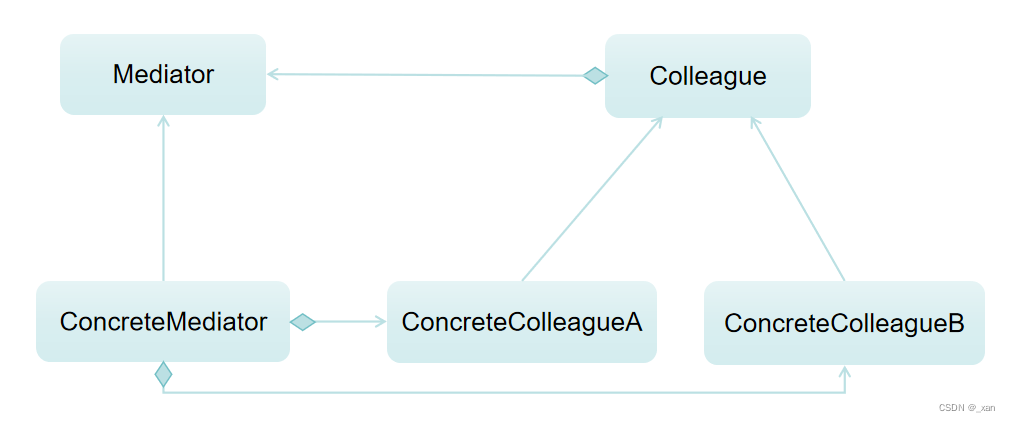
C++设计模式-中介者模式,游戏对象之间的碰撞检测
运行在VS2022,x86,Debug下。 31. 中介者模式 中介者模式允许对象之间通过一个中介者对象进行交互,而不是直接相互引用。可以减少对象之间的直接耦合,同时集中化管理复杂的交互。应用:如在游戏开发中,可以使…...
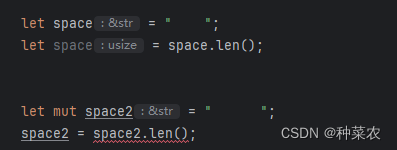
Rust-02-变量与可变性
在Rust中,变量和可变性是两个重要的概念。 变量:变量是用于存储数据的标识符。在Rust中,变量需要声明其类型,例如: let x: i32 5; // 声明一个名为x的变量,类型为i32(整数)&#…...

mov指令中不允许的操作——汇编语言
在 x86 汇编语言中,MOV 指令的限制有助于确保系统的稳定性和正确的操作。下面详细解释为什么这些操作是不允许的。 1. 段寄存器之间直接传送数据 MOV DS, ES ; 错误,不允许原因: 段寄存器是用来定义程序段的开始位置,如代码段…...
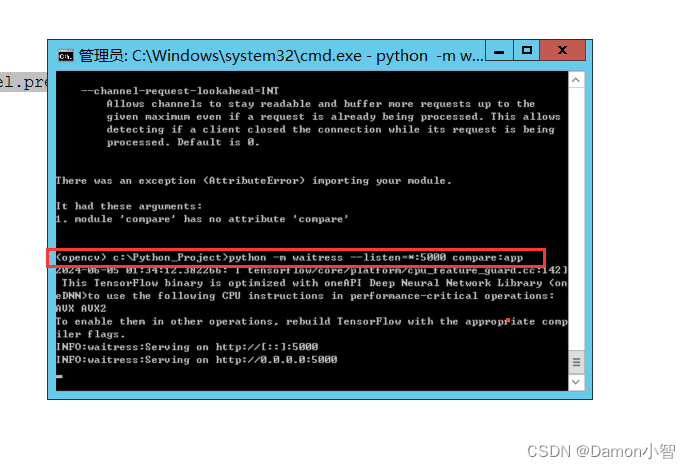
Python进阶-部署Flask项目(以TensorFlow图像识别项目WSGI方式启动为例)
本文详细介绍了如何通过WSGI方式部署一个基于TensorFlow图像识别的Flask项目。首先简要介绍了Flask框架的基本概念及其特点,其次详细阐述了Flask项目的部署流程,涵盖了服务器环境配置、Flask应用的创建与测试、WSGI服务器的安装与配置等内容。本文旨在帮…...

WooYun-2016-199433 -phpmyadmin-反序列化RCE-getshell
参考资料: Phpmyadmin 脚本/设置.php反序列化漏洞 (WooYun-2016-199433)复现_phpmyadmin scriptssetup.php 反序列化漏洞-CSDN博客 https://blog.csdn.net/haoxue__/article/details/129368455利用pearcmd.php文件包含拿shell(L…...
社交“学习伙伴”:Meta Llama助力对话升级
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
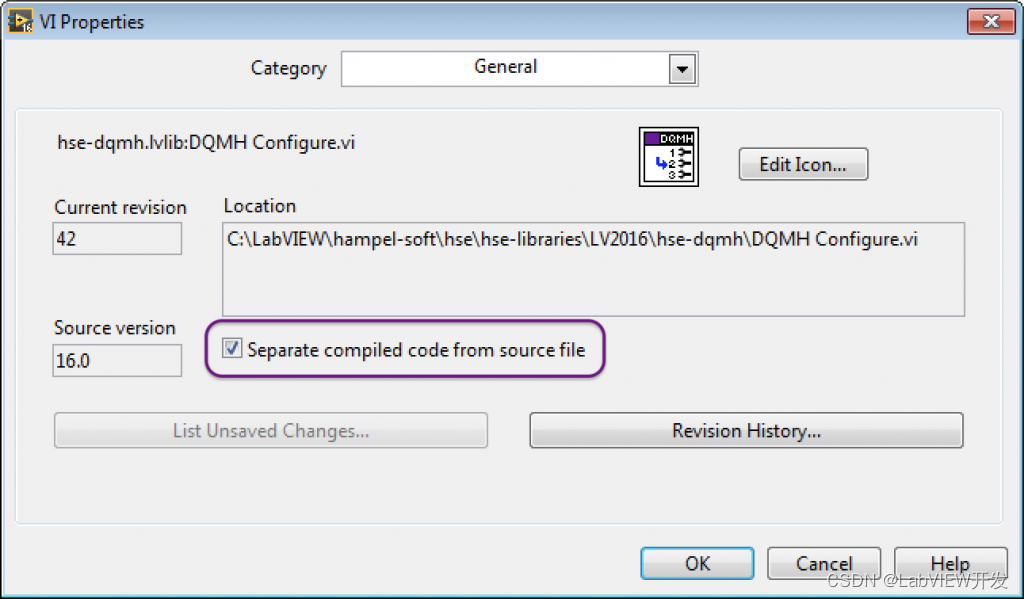
LabVIEW 反向工程的实现与法律地位
什么是LabVIEW反向工程? 反向工程是指从现有的应用程序或软件中推导出其设计、架构、代码等信息的过程。对于LabVIEW而言,反向工程涉及从现有的VI(虚拟仪器)文件、项目或应用程序中提取出设计思路、功能模块、算法实现等。 LabV…...

Python怎么做单元测试
在Python中,最常用的单元测试框架是unittest。以下是如何使用unittest进行单元测试的步骤: 导入unittest模块: 首先,你需要导入unittest模块。 import unittest创建测试类: 你需要创建一个继承自unittest.TestCase的类…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
