Langchain的向量存储 - Document示例代码里的疑问
文章目录
- 前言
- 一、语句分析
- 二、 举例解释
- 三、 完整代码
- 总结
前言
之前的代码里有下面这句话,可能有看不明白的读者。
vectors = [embeddings.embed(doc.page_content) for doc in docs]
今天一起来看下这句话。
一、语句分析
这句话实际上是一个列表推导式,它的作用是遍历 docs 列表中的每个 Document 对象,并将每个 Document 对象的 page_content 属性通过 embeddings.embed 方法转换为向量,然后将所有这些向量组成一个新的列表 vectors。
具体的步骤如下:
- 遍历
docs列表:for doc in docs表示依次取出docs列表中的每个Document对象并赋值给doc。 - 提取
page_content:对于每个Document对象doc,提取其page_content属性(即文档的文本内容)。 - 嵌入转换:将提取到的文本内容通过
embeddings.embed方法转换为向量。embeddings.embed(doc.page_content)返回的是一个向量表示。 - 生成向量列表:将所有转换得到的向量组成一个新的列表,并将该列表赋值给
vectors变量。
这句话不会替换原来的 doc 值,而是生成一个新的向量列表。每个向量对应于 docs 列表中每个 Document 对象的 page_content 的向量表示。
二、 举例解释
假设我们有以下 docs 列表:
docs = [Document(page_content="Machine learning is a method of data analysis.", metadata={"title": "ML Intro"}),Document(page_content="LangChain is a powerful framework.", metadata={"title": "LangChain Overview"})
]
执行这句代码后:
vectors = [embeddings.embed(doc.page_content) for doc in docs]
假设 embeddings.embed 方法将文本转换为一个简单的数值向量,那么 vectors 可能是:
vectors = [[0.1, 0.2, 0.3, 0.4], # 向量表示 "Machine learning is a method of data analysis."[0.5, 0.6, 0.7, 0.8] # 向量表示 "LangChain is a powerful framework."
]
三、 完整代码
以下是一个完整的示例,展示了从文档到向量转换的过程,大家可以一起练一练:
from langchain_core.documents import Document
from langchain.embeddings import OpenAIEmbeddings# 创建文档对象列表
docs = [Document(page_content="Machine learning is a method of data analysis.", metadata={"title": "ML Intro"}),Document(page_content="LangChain is a powerful framework.", metadata={"title": "LangChain Overview"})
]# 初始化嵌入模型
embeddings = OpenAIEmbeddings()# 将文档内容转换为向量
vectors = [embeddings.embed(doc.page_content) for doc in docs]# 输出向量列表
for i, vector in enumerate(vectors):print(f"Vector for doc {i+1}: {vector}")
总结
这句话的主要目的是将每个 Document 对象的文本内容转换为向量,并将所有这些向量组成一个新的列表 vectors,方便后续的向量存储和检索操作。它不会修改原来的 Document 对象,而是生成一个新的向量列表。
相关文章:

Langchain的向量存储 - Document示例代码里的疑问
文章目录 前言一、语句分析二、 举例解释三、 完整代码总结 前言 之前的代码里有下面这句话,可能有看不明白的读者。 vectors [embeddings.embed(doc.page_content) for doc in docs]今天一起来看下这句话。 一、语句分析 这句话实际上是一个列表推导式&#x…...

Docker 教程-介绍-2
快速了解docker有什么。 Docker简介 Docker 是一个开源的应用容器引擎,基于Go语言开发,并遵循Apache 2.0协议。它允许开发者将应用及其依赖包打包进一个可移植的容器中,这些容器可以发布到任何支持Docker的Linux或Windows机器上,…...
 - 三语言AC题解(Python/Java/Cpp))
【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 伐木工(200分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 📎在线评测链接 伐木工(200分) 🌍 评测功能需要订阅专栏后私信联系清隆解…...

UltraScale+系列模块化仪器,可以同时用作控制器、算法加速器和高速数字信号处理器
基于 XCZU7EG / XCZU4EG / XCZU2EG • 灵活的模块组合 • 易于嵌入的紧凑型外观结构 • 高性能的 ARM Cortex 处理器 • 成熟的 FPGA 可编程逻辑 ,基于 IP 核的软件库 基于 Xilinx Zynq UltraScaleMPSoC 的 FPGA 技术,采用 Xilinx Zynq UltraScale&a…...
相比有哪些优势?)
Python与其他编程语言(如Java、C++)相比有哪些优势?
一、技术难点 在探讨Python与其他编程语言相比的优势时,技术难点在于如何全面、准确地把握并阐述这些优势。这需要对Python、Java、C等编程语言有深入的理解,包括它们的语法特性、应用领域、性能特点、开发效率等。 首先,Python的语法简洁明…...

Edge浏览器双击关闭标签页,双击关闭浏览器选项卡
设置》外观》自定义浏览器,开启“使用双击关闭浏览器选项卡” 设置里面搜索“双击”,这是最快的方式 鼠标滚轮单击 或者进入“设置”-“辅助功能” 呼吁已久的功能来了!Edge浏览器双击关闭标签页功能上线新 国产浏览器大多都有双击关闭标签页…...

C++ 贪心算法——跳跃游戏、划分字母区间
一:跳跃游戏 55. 跳跃游戏 题目描述:给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个下标,如果可以,返回 true ࿱…...

汽车数据应用构想(三)
上期说的,用数据去拟合停车信息的应用,那么类似的POI信息相关的场景其实都可以实现。今天讲讲用户使用频率也很高的加油/充电场景。 实际应用中,在加油场景中用户关心的通常还是价格。无论是导航还是各种加油APP/小程序,都已经很…...

体素技术在AI绘画中的革新作用
随着人工智能技术的不断进步,AI绘画已经成为艺术创作和视觉设计领域的一大趋势。在众多推动AI绘画发展的技术中,体素技术以其独特的优势,正在逐渐改变着我们对计算机生成图像的认识。本文旨在探讨体素技术在AI绘画中的应用与影响,…...

Leetcode.866 回文质数
题目链接 Leetcode.866 回文质数 rating : 1938 题目描述 给你一个整数 n n n ,返回大于或等于 n n n 的最小 回文质数。 一个整数如果恰好有两个除数: 1 1 1 和它本身,那么它是 质数 。注意, 1 1 1 不是质数。 例如…...
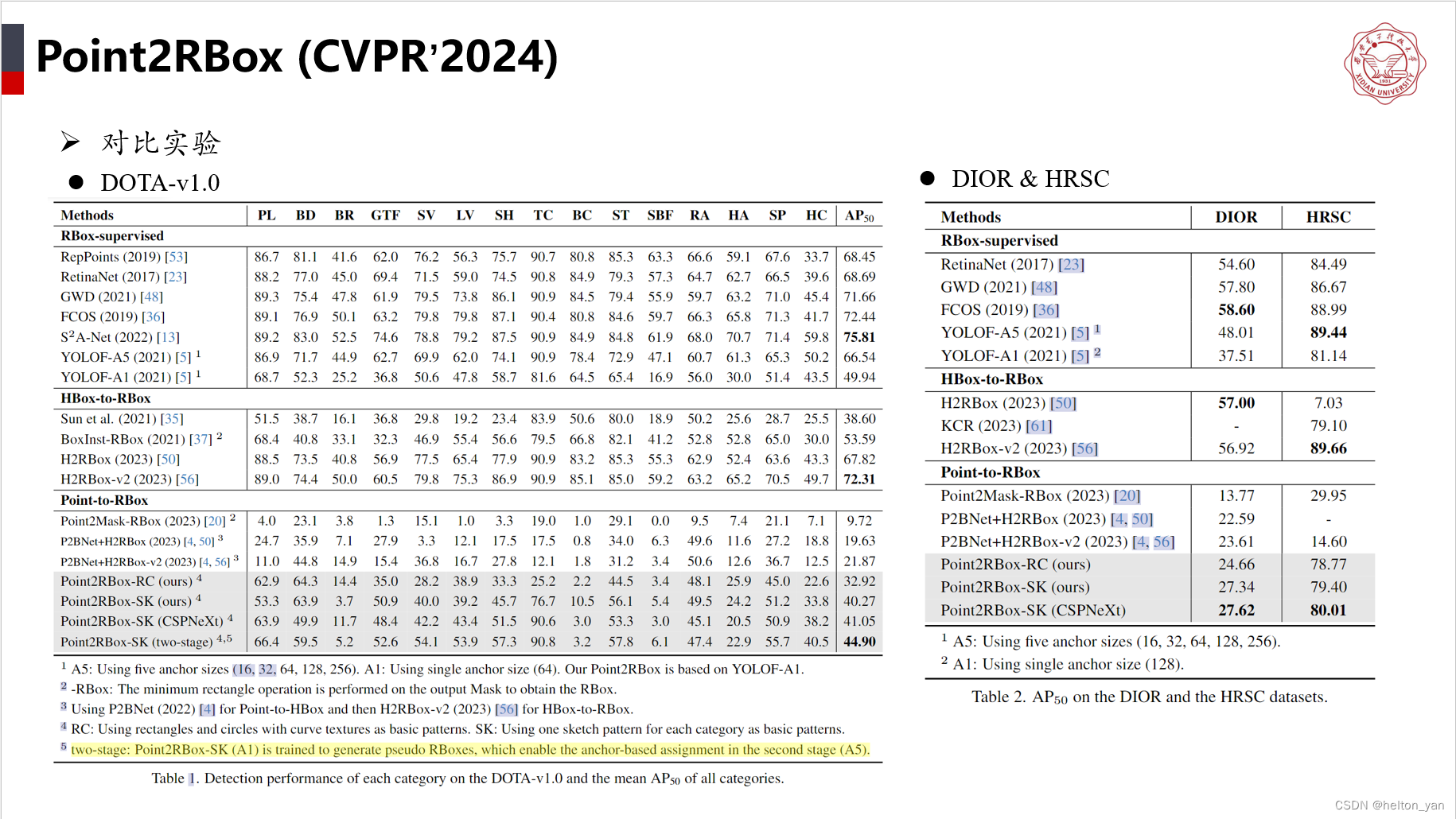
【论文阅读】Point2RBox (CVPR’2024)
paper:https://arxiv.org/abs/2311.14758 code:https://github.com/yuyi1005/point2rbox-mmrotate...

深度学习的点云分割
深度学习的点云分割 点云分割是计算机视觉中的一个重要任务,特别是在三维数据处理和分析中。点云数据是由大量三维点构成的集合,每个点包含空间坐标(x, y, z),有时还包含其他信息如颜色和法向量。点云分割的目标是将点…...

【知识点】c++模板特化
在 C 中,模板特化分为全特化(full specialization)和偏特化(partial specialization)。它们允许程序员为特定类型或类型模式提供不同的实现,以覆盖通用模板的默认行为。 模板全特化 模板全特化是指为某个…...

算法家族之一——二分法
目录 算法算法的打印效果如果算法里的整型“i”为1如果算法里的整型“i”为11 算法的流程图算法的实际应用总结 大家好,我叫 这是我58,现在,请看下面的算法。 算法 #define _CRT_SECURE_NO_WARNINGS 1//<--预处理指令 #include <stdi…...
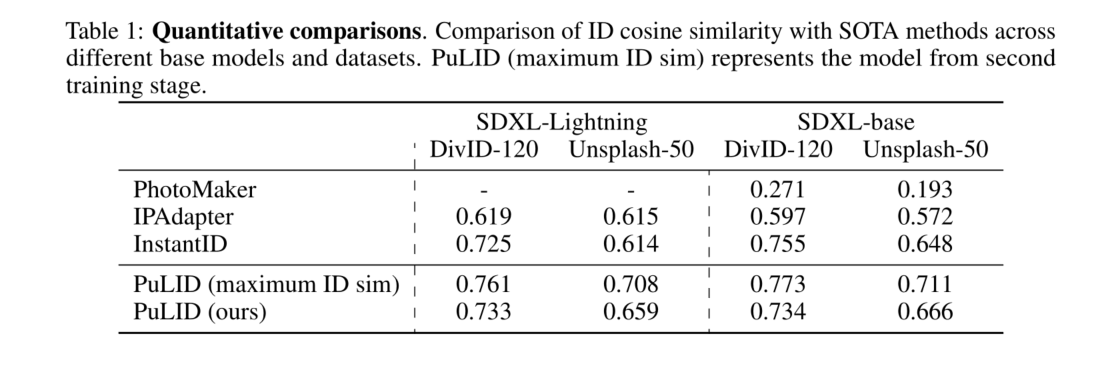
【深度学习】PuLID: Pure and Lightning ID Customization via Contrastive Alignment
论文:https://arxiv.org/abs/2404.16022 代码:https://github.com/ToTheBeginning/PuLID 文章目录 AbstractIntroductionRelated WorkMethods Abstract 我们提出了一种新颖的、无需调整的文本生成图像ID定制方法——Pure and Lightning ID customizatio…...

Elastic 8.14:用于简化分析的 Elasticsearch 查询语言 (ES|QL) 正式发布
作者:来自 Elastic Brian Bergholm 今天,我们很高兴地宣布 Elastic 8.14 正式发布。 什么是新的? 8.14 版本最重要的标题是 ES|QL 的正式发布(GA),它是从头开始设计和专门构建的,可大大简化数据调查。在新的查询引擎的…...

C语言指针与数组的区别
在C语言中,指针和数组虽然在很多情况下可以互换使用,但它们在概念上和行为上存在一些区别。下面详细解释这些区别: ### 数组 1. **固定大小**:数组在声明时必须指定大小,这个大小在编译时确定,之后不能改…...

springboot3一些听课笔记
文章目录 一、错误处理机制1.1 默认1.2 自定义 二、嵌入式容器 一、错误处理机制 1.1 默认 错误处理的自动配置都在ErrorMvcAutoConfiguration中,两大核心机制: ● 1. SpringBoot 会自适应处理错误,响应页面或JSON数据 ● 2. SpringMVC的错…...

【小沐学Python】Python实现Web服务器(CentOS下打包Flask)
文章目录 1、简介2、下载Python3、编译Python4、安装PyInstaller5、打包PyInstaller6、相关问题6.1 ImportError: urllib3 v2 only supports OpenSSL 1.1.1, currently the ssl module is compiled with OpenSSL 1.0.2k-fips 26 Jan 2017. See: https://github.com/urllib3/url…...

Cesium开发环境搭建(一)
1.下载安装Node.js 进入官网地址下载安装包 Node.js — Download Node.js https://cdn.npmmirror.com/binaries/node/ 选择对应你系统的Node.js版本,这里我选择的是Windows系统、64位 安装完成后,WINR,输入node --version,显示…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...
