html5实现个人网站源码
文章目录
- 1.设计来源
- 1.1 网站首页页面
- 1.2 个人工具页面
- 1.3 个人日志页面
- 1.4 个人相册页面
- 1.5 给我留言页面
- 2.效果和源码
- 2.1 动态效果
- 2.2 目录结构
- 源码下载
作者:xcLeigh
文章地址:https://blog.csdn.net/weixin_43151418/article/details/139564407
html5实现个人网站源码,html5实现个人网站源码,大作业网站源码,源码有五个页面,网站首页,个人工具,个人日志,个人相册,给我留言等模块,内容可以自己调整,自定义导航菜单,轮播图,自定义标签项,代码简单,上手快,模板通俗易懂,可以在此模板上改文字描述就行。可以直接使用。也可直接预览效果。
1.设计来源
1.1 网站首页页面
网站首页页面,展示个人相关信息,个人常用的工具网站地址,个人的日常照片集,相关的朋友间的评价等等信息,可以根据自己的需求加减内容。

1.2 个人工具页面
个人工具页面,展示自己平时用的工具网站,源码网站,学习网站,便于自己快速的进入网站,记录链接。

1.3 个人日志页面
个人日志页面,记录自己的有意义的事情,写下自己的高兴的事,分享给大家,可以在此基础上扩展类型,点赞等,根据自己的需求来。

1.4 个人相册页面
个人相册页面,记录自己的生活所拍摄的美景,自己的美图,好看、新颖的事物,可以自己加上根据类型展示,加上相册备注等等扩展,根据自己的需求来。

1.5 给我留言页面
给我留言页面,根据昵称、主题、内容等信息给我留言,这里是静态的,可以根据自己的需求扩展。

2.效果和源码
2.1 动态效果
这里是完整的效果演示,可在此代码基础上更加完善功能,支持扩展自己的风格,可以删减内容,打造属于自己的个人网站。
html5实现个人网站源码
2.2 目录结构
这里是代码的目录结构,见下面的 源码下载 ,里面有所有代码资源和相关说明。

源码下载
html5实现个人网站源码(源码) 点击下载

💢 关注博主 带你实现畅游前后端
🏰 加入社区 带你体验马航不孤单
💯 神秘个人简介 带你体验不一样得介绍
💘 为爱表白 为你那个TA,体验别致的浪漫惊喜
🎀 酷炫邀请函 带你体验高大上得邀请
① 🉑提供云服务部署(有自己的阿里云);
② 🉑提供前端、后端、应用程序、H5、小程序、公众号等相关业务;
如🈶合作请联系我,期待您的联系。
注:本文撰写于CSDN平台,作者:xcLeigh(所有权归作者所有),https://blog.csdn.net/weixin_43151418,如果相关下载没有跳转,请查看这个地址,相关链接没有跳转,皆是抄袭本文,转载请备注本文原地址。
亲,码字不易,动动小手,欢迎 点赞 ➕ 收藏,如 🈶 问题请留言(评论),博主看见后一定及时给您答复,💌💌💌
原文地址:https://blog.csdn.net/weixin_43151418/article/details/139564407(防止抄袭,原文地址不可删除)
相关文章:

html5实现个人网站源码
文章目录 1.设计来源1.1 网站首页页面1.2 个人工具页面1.3 个人日志页面1.4 个人相册页面1.5 给我留言页面 2.效果和源码2.1 动态效果2.2 目录结构 源码下载 作者:xcLeigh 文章地址:https://blog.csdn.net/weixin_43151418/article/details/139564407 ht…...

【内存管理】内存布局
ARM32位系统的内存布局图 32位操作系统的内存布局很经典,很多书籍都是以32位系统为例子去讲解的。32位的系统可访问的地址空间为4GB,用户空间为1GB ~ 3GB,内核空间为3GB ~ 4GB。 为什么要划分为用户空间和内核空间呢? 一般处理器…...

软件试运行方案(Word)
软件试运行方案(直接套用实际项目,原件获取通过本文末个人名片直接获取。) 一、试运行目的 二、试运行的准备 三、试运行时间 四、试运行制度 五、试运行具体内容与要求...
Redis原理篇——哨兵机制
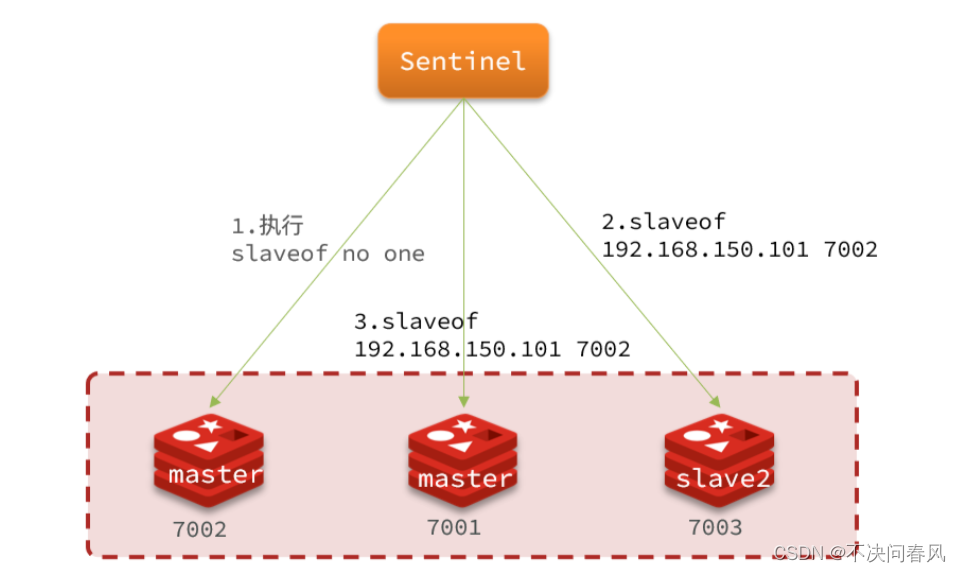
Redis原理篇——哨兵机制 1.Redis哨兵2.哨兵工作原理2.1.哨兵作用2.2.状态监控2.3.选举leader2.4.failover 1.Redis哨兵 主从结构中master节点的作用非常重要,一旦故障就会导致集群不可用。那么有什么办法能保证主从集群的高可用性呢? 2.哨兵工作原理 …...

web前端的MySQL:跨领域之旅的探索与困惑
web前端的MySQL:跨领域之旅的探索与困惑 在数字化浪潮的推动下,web前端与MySQL数据库似乎成为了两个不可或缺的领域。然而,当我们将这两者放在一起,尝试探索web前端与MySQL之间的交互与关联时,却发现这是一次充满困惑…...
Postgresql源码(135)生成执行计划——Var的调整set_plan_references
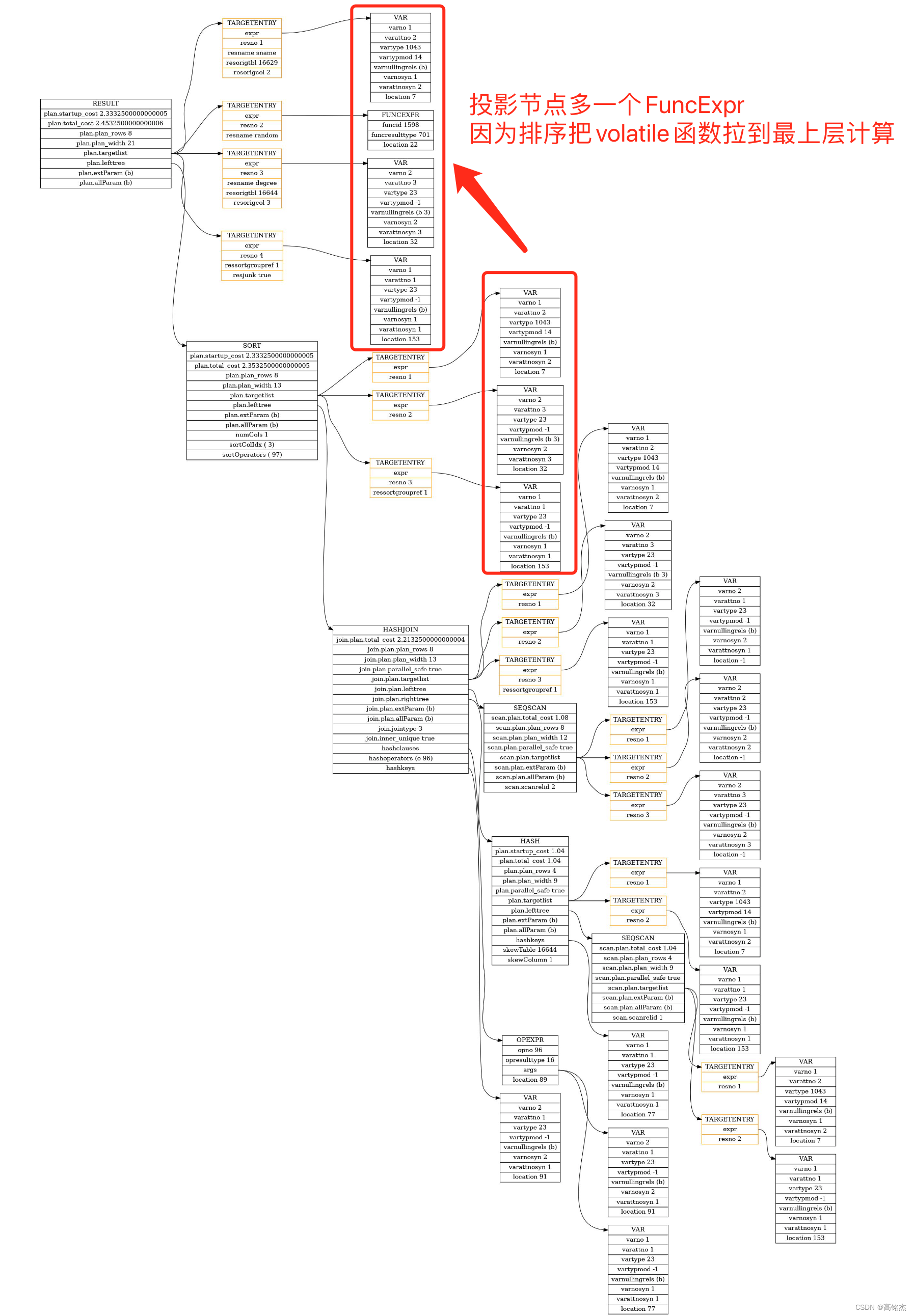
1 总结 set_plan_references主要有两个功能: 拉平:生成拉平后的RTE列表(add_rtes_to_flat_rtable)。调整:调整前每一层计划中varno的引用都是相对于本层RTE的偏移量。放在一个整体计划后,需要指向一个统一…...

Python魔法之旅专栏(导航)
目录 推荐阅读 1、Python筑基之旅 2、Python函数之旅 3、Python算法之旅 4、博客个人主页 首先,感谢老铁们一直以来对我的支持与厚爱,让我能坚持把Python魔法方法专栏更新完毕! 其次,为了方便大家查阅,我将此专栏…...
Python第二语言(五、Python文件相关操作)
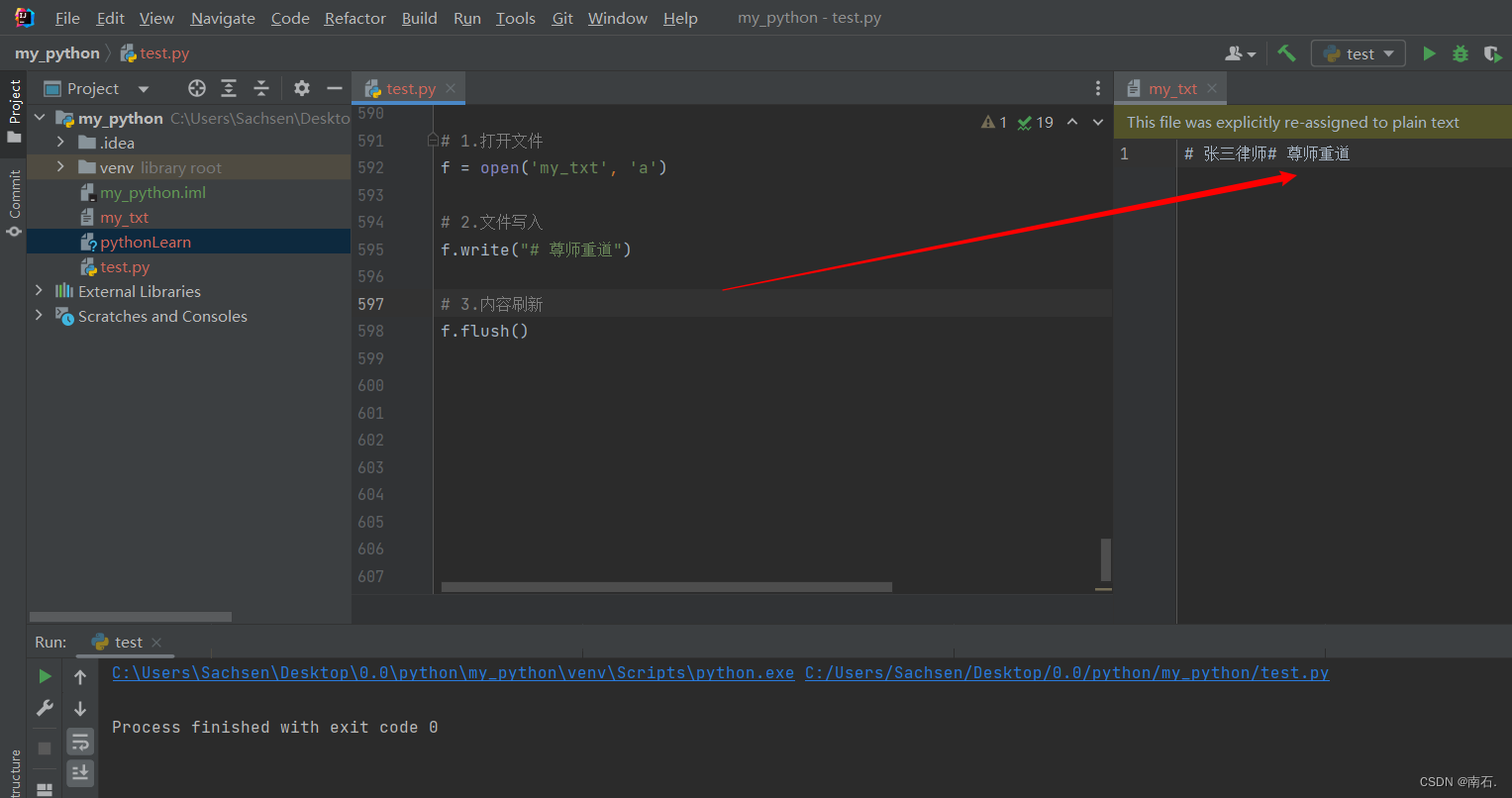
目录 1. 文件编码的概念 2. 文件的读取操作 2.1 什么是文件 2.2 open()打开函数 2.3 mode常用的三种基础访问模式 2.4 文件操作及案例 3. 文件的写入操作及刷新文件:write与flush 4. 文件的追加操作 5. 文件操作的综合案例(文件备份操作&#x…...
)
Vue3 组合式 API:依赖注入(四)
provide() provide() 函数是用于依赖注入的一个关键部分。这个函数允许你在组件树中提供一个值或对象,使得任何子组件(无论层级多深)都能够通过 inject() 函数来访问这些值。 import { provide, ref } from vue; export default { setup(…...

Vue如何引入ElementUI并使用
Element UI详细介绍 Element UI是一个基于Vue 2.0的桌面端组件库,旨在构建简洁、快速的用户界面。由饿了么前端团队开发,提供丰富的组件和工具,帮助开发者快速构建高质量的Vue应用,并且以开放源代码的形式提供。 1. VueElementU…...
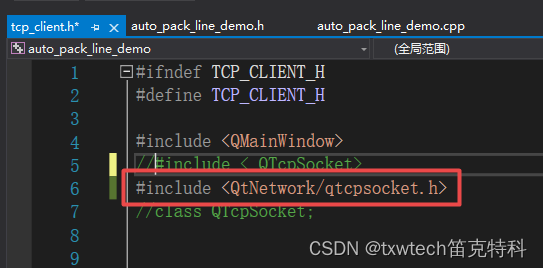
VS2019 QT无法打开 源 文件 “QTcpSocket“
VS2019 QT无法打开 源 文件 "QTcpSocket" QT5.15.2_msvc2019_64 严重性 代码 说明 项目 文件 行 禁止显示状态 错误(活动) E1696 无法打开 源 文件 "QTcpSocket" auto_pack_line_demo D:\vs_qt_project\auto_pack_line_de…...
【Golang】Map 稳定有序遍历的实现与探索:保序遍历之道
【Golang】Map 稳定有序遍历的实现与探索:保序遍历之道 大家好 我是寸铁👊 总结了一篇【Golang】Map 稳定有序遍历的实现与探索:保序遍历之道✨ 喜欢的小伙伴可以点点关注 💝 前言🍎 在计算机科学中,数据结…...

使用Nextjs学习(学习+项目完整版本)
创建项目 运行如下命令 npx create-next-app next-create创建项目中出现的各种提示直接走默认的就行,一直回车就行了 创建完成后进入到项目运行localhost:3000访问页面,如果和我下面页面一样就是创建项目成功了 整理项目 将app/globals.css里面的样式都删除,只留下最上面三…...

KUKA机器人KRC5控制柜面板LED显示
对于KUKA机器人新系列控制柜KRC5控制柜来说,其控制柜面板LED布局如下图: 其中①②③④分别为: 1、机器人控制柜处于不同状态时,LED显示如下: 2、机器人控制柜正在运行时: 3、机器人控制柜运行时出现的故障…...

为什么选择Python作为AI开发语言
为什么Python适合AI 在当前的科技浪潮中,人工智能(AI)无疑是最热门的话题之一。无论是自动驾驶、智能推荐还是自然语言处理,AI都在不断改变我们的生活。而在这场技术革命中,Python作为主要的编程语言之一,…...

【算法篇】求最长公共前缀JavaScript版本
题目描述 给你一个大小为 n 的字符串数组 strs ,其中包含n个字符串 , 编写一个函数来查找字符串数组中的最长公共前缀,返回这个公共前缀。 数据范围: 数据范围:0<n<5000,0<len(strsi)< 5000 进阶:空间复杂度 O(1)&a…...
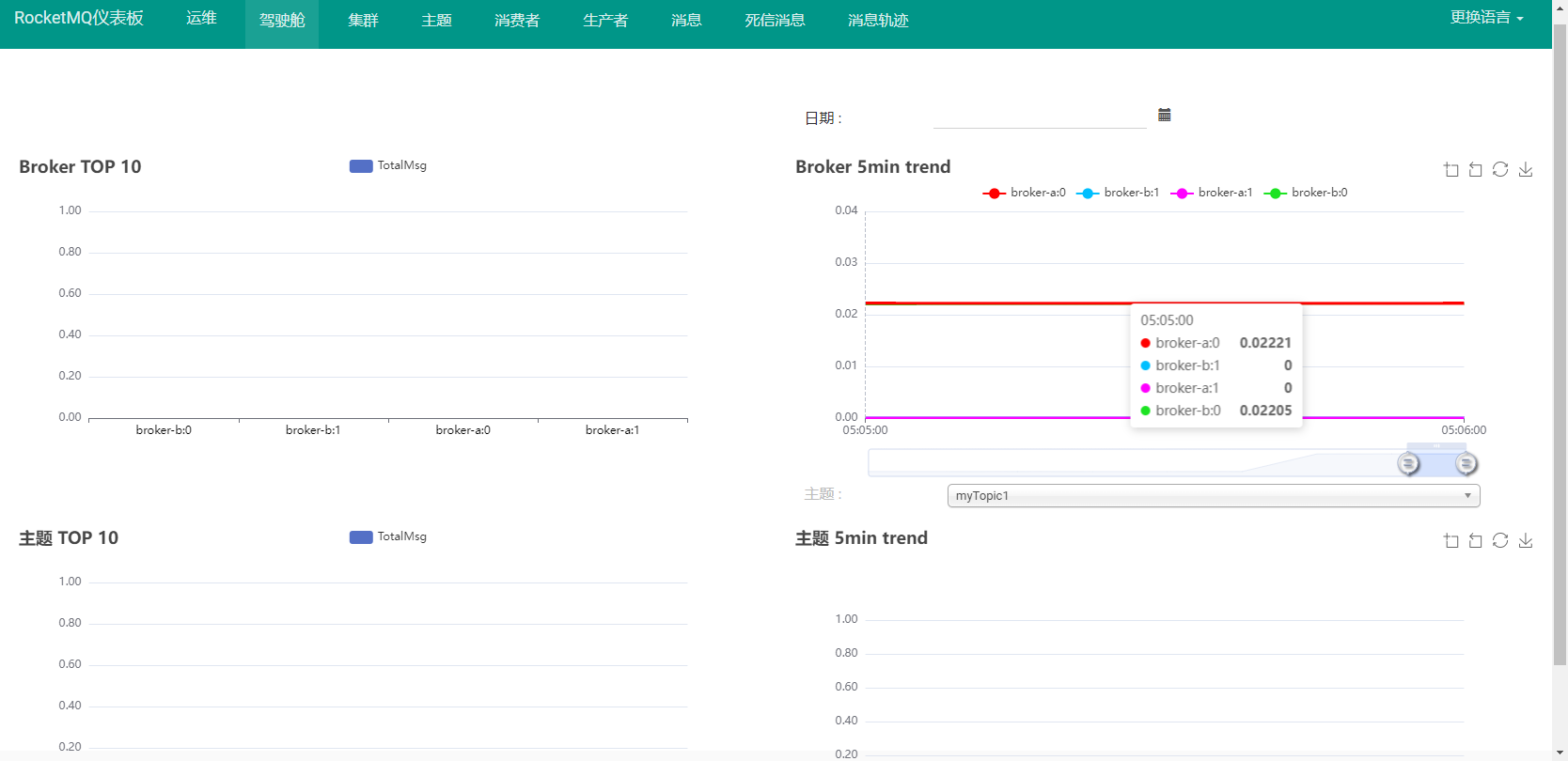
搭建RocketMQ主从异步集群
搭建RocketMQ主从异步集群 1、RocketMQ集群模式 为了追求更好的性能,RocketMQ的最佳实践方式都是在集群模式下完成的。RocketMQ官方提供了三种集群搭建方式: 2主2从异步通信方式:使用异步方式进行主从之间的数据复制。吞吐量大,…...

最大子段和问题
最大子段和问题 分数 15 全屏浏览 切换布局 作者 王东 单位 贵州师范学院 最大子段和问题。给定由n个整数组成的序列,求序列中子段的最大和,若所有整数均为负整数时定义最大子段和为0。 输入格式: 第一行输入整数个数n(1≤n≤1000&…...
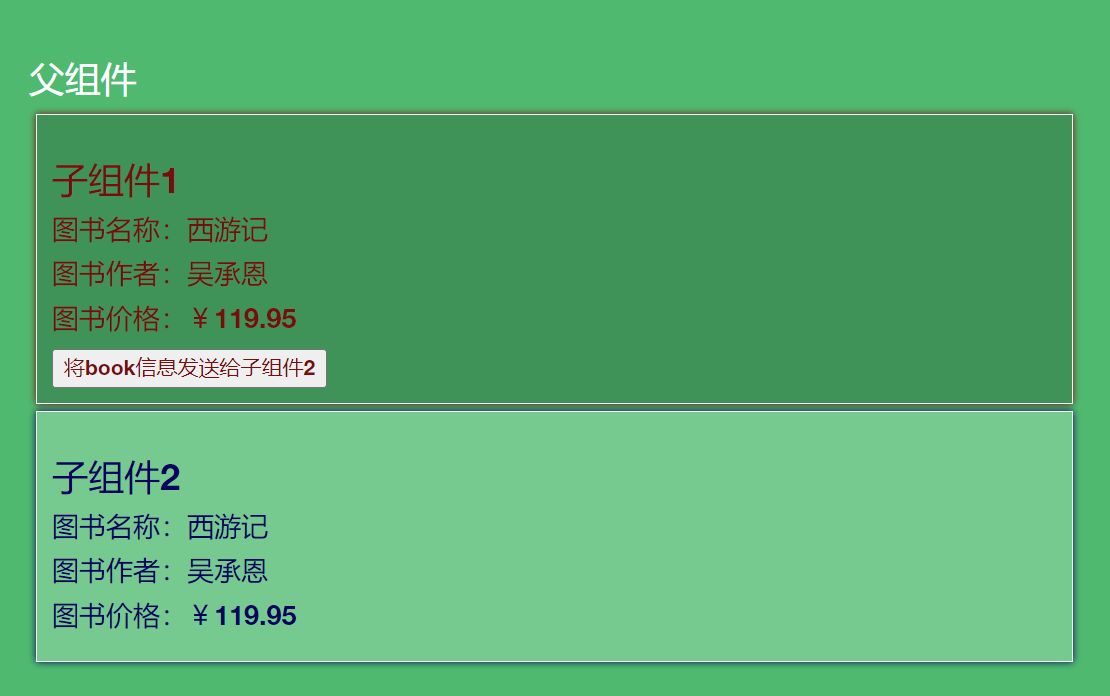
Vue3中的常见组件通信之mitt
Vue3中的常见组件通信之mitt 概述 在vue3中常见的组件通信有props、mitt、v-model、 r e f s 、 refs、 refs、parent、provide、inject、pinia、slot等。不同的组件关系用不同的传递方式。常见的撘配形式如下表所示。 组件关系传递方式父传子1. props2. v-model3. $refs…...
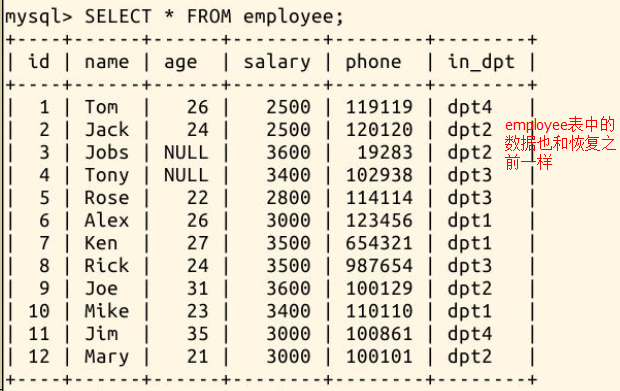
MySQL快速入门(极简)
SQL 介绍及 MySQL 安装 一、实验简介 本课程为实验楼提供的 MySQL 实验教程,所有的步骤都在实验楼在线实验环境中完成,学习中请按照实验步骤依次操作。 本课程为 SQL 基本语法及 MySQL 基本操作的实验,理论内容较少,动手实践多…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
