让GNSSRTK不再难【第二天-第7部分2】
状态更新计算过程:
-
计算卡尔曼增益:
根据预测的误差协方差矩阵 P k − P_k^- Pk− 和观测噪声协方差矩阵 R R R 计算卡尔曼增益 K k K_k Kk:
K k = P k − H T ( H P k − H T + R ) − 1 K_k = P_k^- H^T (H P_k^- H^T + R)^{-1} Kk=Pk−HT(HPk−HT+R)−1带入预测的 P k − P_k^- Pk− 和 R R R 计算:
P k − = [ C o v X X 0 0 0 0 0 0 C o v Y Y 0 0 0 0 0 0 C o v Z Z 0 0 0 0 0 0 C o v δ t δ t 0 0 0 0 0 0 ∗ ∗ 0 0 0 0 ∗ ∗ ] P_k^- = \begin{bmatrix} Cov_{XX} & 0 & 0 & 0 & 0 & 0 \\ 0 & Cov_{YY} & 0 & 0 & 0 & 0 \\ 0 & 0 & Cov_{ZZ} & 0 & 0 & 0 \\ 0 & 0 & 0 & Cov_{\delta t \delta t} & 0 & 0 \\ 0 & 0 & 0 & 0 & * & * \\ 0 & 0 & 0 & 0 & * & * \\ \end{bmatrix} Pk−= CovXX000000CovYY000000CovZZ000000Covδtδt000000∗∗0000∗∗
R = [ σ 1 2 0 ⋯ 0 0 σ 2 2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ σ n 2 ] R = \begin{bmatrix} \sigma_1^2 & 0 & \cdots & 0 \\ 0 & \sigma_2^2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma_n^2 \\ \end{bmatrix} R= σ120⋮00σ22⋮0⋯⋯⋱⋯00⋮σn2
假设观测矩阵 H H H 为设计矩阵 A A A:
A = [ l f 1 G 1 m f 1 G 1 n f 1 G 1 − 1 0 0 0 l f 2 G 2 m f 2 G 2 n f 2 G 2 − 1 0 0 0 l f 3 G 3 m f 3 G 3 n f 3 G 3 − 1 0 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ l f n G n m f n G n n f n G n − 1 0 0 0 l f 1 C 1 m f 1 C 1 n f 1 C 1 − 1 0 − 1 0 l f 2 C 2 m f 2 C 2 n f 2 C 2 − 1 0 − 1 0 l f 3 C 3 m f 3 C 3 n f 3 C 3 − 1 0 − 1 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ l f n C n m f n C n n f n C n − 1 0 − 1 0 ] A = \begin{bmatrix} l_{f_1}^{G_1} & m_{f_1}^{G_1} & n_{f_1}^{G_1} & -1 & 0 & 0 & 0 \\ l_{f_2}^{G_2} & m_{f_2}^{G_2} & n_{f_2}^{G_2} & -1 & 0 & 0 & 0 \\ l_{f_3}^{G_3} & m_{f_3}^{G_3} & n_{f_3}^{G_3} & -1 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ l_{f_n}^{G_n} & m_{f_n}^{G_n} & n_{f_n}^{G_n} & -1 & 0 & 0 & 0 \\ l_{f_1}^{C_1} & m_{f_1}^{C_1} & n_{f_1}^{C_1} & -1 & 0 & -1 & 0 \\ l_{f_2}^{C_2} & m_{f_2}^{C_2} & n_{f_2}^{C_2} & -1 & 0 & -1 & 0 \\ l_{f_3}^{C_3} & m_{f_3}^{C_3} & n_{f_3}^{C_3} & -1 & 0 & -1 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ l_{f_n}^{C_n} & m_{f_n}^{C_n} & n_{f_n}^{C_n} & -1 & 0 & -1 & 0 \end{bmatrix} A= lf1G1lf2G2lf3G3⋮lfnGnlf1C1lf2C2lf3C3⋮lfnCnmf1G1mf2G2mf3G3⋮mfnGnmf1C1mf2C2mf3C3⋮mfnCnnf1G1nf2G2nf3G3⋮nfnGnnf1C1nf2C2nf3C3⋮nfnCn−1−1−1⋮−1−1−1−1⋮−1000⋮0000⋮0000⋮0−1−1−1⋮−1000⋮0000⋮0
则卡尔曼增益 K k K_k Kk 计算为:
K k = P k − A T ( A P k − A T + R ) − 1 K_k = P_k^- A^T (A P_k^- A^T + R)^{-1} Kk=Pk−AT(APk−AT+R)−1(1)计算 A P k − A T A P_k^- A^T APk−AT:
A P k − A T = A [ C o v X X 0 0 0 0 0 0 C o v Y Y 0 0 0 0 0 0 C o v Z Z 0 0 0 0 0 0 C o v δ t δ t 0 0 0 0 0 0 ∗ ∗ 0 0 0 0 ∗ ∗ ] A T A P_k^- A^T = A \begin{bmatrix} Cov_{XX} & 0 & 0 & 0 & 0 & 0 \\ 0 & Cov_{YY} & 0 & 0 & 0 & 0 \\ 0 & 0 & Cov_{ZZ} & 0 & 0 & 0 \\ 0 & 0 & 0 & Cov_{\delta t \delta t} & 0 & 0 \\ 0 & 0 & 0 & 0 & * & * \\ 0 & 0 & 0 & 0 & * & * \\ \end{bmatrix} A^T APk−AT=A CovXX000000CovYY000000CovZZ000000Covδtδt000000∗∗0000∗∗ AT(2)计算 A P k − A T + R A P_k^- A^T + R APk−AT+R:
A P k − A T + R = A [ C o v X X 0 0 0 0 0 0 C o v Y Y 0 0 0 0 0 0 C o v Z Z 0 0 0 0 0 0 C o v δ t δ t 0 0 0 0 0 0 ∗ ∗ 0 0 0 0 ∗ ∗ ] A T + R A P_k^- A^T + R = A \begin{bmatrix} Cov_{XX} & 0 & 0 & 0 & 0 & 0 \\ 0 & Cov_{YY} & 0 & 0 & 0 & 0 \\ 0 & 0 & Cov_{ZZ} & 0 & 0 & 0 \\ 0 & 0 & 0 & Cov_{\delta t \delta t} & 0 & 0 \\ 0 & 0 & 0 & 0 & * & * \\ 0 & 0 & 0 & 0 & * & * \\ \end{bmatrix} A^T + R APk−AT+R=A CovXX000000CovYY000000CovZZ000000Covδtδt000000∗∗0000∗∗ AT+R由于 A P k − A T + R A P_k^- A^T + R APk−AT+R 是对角矩阵,其逆矩阵为:
( A P k − A T + R ) − 1 = [ ( C o v X X + σ 1 2 ) − 1 0 0 0 ( C o v Y Y + σ 2 2 ) − 1 0 0 0 ( C o v Z Z + σ 3 2 ) − 1 ] (A P_k^- A^T + R)^{-1} = \begin{bmatrix} (Cov_{XX} + \sigma_1^2)^{-1} & 0 & 0 \\ 0 & (Cov_{YY} + \sigma_2^2)^{-1} & 0 \\ 0 & 0 & (Cov_{ZZ} + \sigma_3^2)^{-1} \\ \end{bmatrix} (APk−AT+R)−1= (CovXX+σ12)−1000(CovYY+σ22)−1000(CovZZ+σ32)−1 (3)计算 K k K_k Kk:
K k = P k − A T ( A P k − A T + R ) − 1 K_k = P_k^- A^T (A P_k^- A^T + R)^{-1} Kk=Pk−AT(APk−AT+R)−1带入 P k − P_k^- Pk− 和 ( A P k − A T + R ) − 1 (A P_k^- A^T + R)^{-1} (APk−AT+R)−1:
K k = [ C o v X X 0 0 0 C o v Y Y 0 0 0 C o v Z Z 0 0 0 0 0 0 0 0 0 0 0 0 ] A T [ ( C o v X X + σ 1 2 ) − 1 0 0 0 ( C o v Y Y + σ 2 2 ) − 1 0 0 0 ( C o v Z Z + σ 3 2 ) − 1 ] K_k = \begin{bmatrix} Cov_{XX} & 0 & 0 \\ 0 & Cov_{YY} & 0 \\ 0 & 0 & Cov_{ZZ} \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} A^T \begin{bmatrix} (Cov_{XX} + \sigma_1^2)^{-1} & 0 & 0 \\ 0 & (Cov_{YY} + \sigma_2^2)^{-1} & 0 \\ 0 & 0 & (Cov_{ZZ} + \sigma_3^2)^{-1} \\ \end{bmatrix} Kk= CovXX0000000CovYY0000000CovZZ0000 AT (CovXX+σ12)−1000(CovYY+σ22)−1000(CovZZ+σ32)−1 简化计算得到:
K k = [ C o v X X ( C o v X X + σ 1 2 ) − 1 0 0 0 C o v Y Y ( C o v Y Y + σ 2 2 ) − 1 0 0 0 C o v Z Z ( C o v Z Z + σ 3 2 ) − 1 0 0 0 0 0 0 0 0 0 0 0 0 ] K_k = \begin{bmatrix} Cov_{XX} (Cov_{XX} + \sigma_1^2)^{-1} & 0 & 0 \\ 0 & Cov_{YY} (Cov_{YY} + \sigma_2^2)^{-1} & 0 \\ 0 & 0 & Cov_{ZZ} (Cov_{ZZ} + \sigma_3^2)^{-1} \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} Kk= CovXX(CovXX+σ12)−10000000CovYY(CovYY+σ22)−10000000CovZZ(CovZZ+σ32)−10000 因此,卡尔曼增益 K k K_k Kk 为:
K k = [ C o v X X C o v X X + σ 1 2 0 0 0 C o v Y Y C o v Y Y + σ 2 2 0 0 0 C o v Z Z C o v Z Z + σ 3 2 0 0 0 0 0 0 0 0 0 0 0 0 ] K_k = \begin{bmatrix} \frac{Cov_{XX}}{Cov_{XX} + \sigma_1^2} & 0 & 0 \\ 0 & \frac{Cov_{YY}}{Cov_{YY} + \sigma_2^2} & 0 \\ 0 & 0 & \frac{Cov_{ZZ}}{Cov_{ZZ} + \sigma_3^2} \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} Kk= CovXX+σ12CovXX0000000CovYY+σ22CovYY0000000CovZZ+σ32CovZZ0000 -
更新状态估计:
根据观测值 z k z_k zk 和预测值 x ^ k − \hat{x}_k^- x^k− 进行状态更新:
x k = x ^ k − + K k ( z k − H x ^ k − ) x_k = \hat{x}_k^- + K_k (z_k - H \hat{x}_k^-) xk=x^k−+Kk(zk−Hx^k−)带入观测值 z k z_k zk 和预测值 x ^ k − \hat{x}_k^- x^k−:
假设 x ^ k − \hat{x}_k^- x^k− 为:
x ^ k − = [ x ^ k , 1 − x ^ k , 2 − x ^ k , 3 − ⋮ x ^ k , 7 − ] \hat{x}_k^- = \begin{bmatrix} \hat{x}_{k,1}^- \\ \hat{x}_{k,2}^- \\ \hat{x}_{k,3}^- \\ \vdots \\ \hat{x}_{k,7}^- \end{bmatrix} x^k−= x^k,1−x^k,2−x^k,3−⋮x^k,7− 观测值 z k z_k zk 为:
z k = [ z k , 1 z k , 2 z k , 3 ] z_k = \begin{bmatrix} z_{k,1} \\ z_{k,2} \\ z_{k,3} \end{bmatrix} zk= zk,1zk,2zk,3 假设观测矩阵 H H H 为设计矩阵 A A A:
A = [ l f 1 G 1 m f 1 G 1 n f 1 G 1 − 1 0 0 0 l f 2 G 2 m f 2 G 2 n f 2 G 2 − 1 0 0 0 l f 3 G 3 m f 3 G 3 n f 3 G 3 − 1 0 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ l f n G n m f n G n n f n G n − 1 0 0 0 l f 1 C 1 m f 1 C 1 n f 1 C 1 − 1 0 − 1 0 l f 2 C 2 m f 2 C 2 n f 2 C 2 − 1 0 − 1 0 l f 3 C 3 m f 3 C 3 n f 3 C 3 − 1 0 − 1 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ l f n C n m f n C n n f n C n − 1 0 − 1 0 ] A = \begin{bmatrix} l_{f_1}^{G_1} & m_{f_1}^{G_1} & n_{f_1}^{G_1} & -1 & 0 & 0 & 0 \\ l_{f_2}^{G_2} & m_{f_2}^{G_2} & n_{f_2}^{G_2} & -1 & 0 & 0 & 0 \\ l_{f_3}^{G_3} & m_{f_3}^{G_3} & n_{f_3}^{G_3} & -1 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ l_{f_n}^{G_n} & m_{f_n}^{G_n} & n_{f_n}^{G_n} & -1 & 0 & 0 & 0 \\ l_{f_1}^{C_1} & m_{f_1}^{C_1} & n_{f_1}^{C_1} & -1 & 0 & -1 & 0 \\ l_{f_2}^{C_2} & m_{f_2}^{C_2} & n_{f_2}^{C_2} & -1 & 0 & -1 & 0 \\ l_{f_3}^{C_3} & m_{f_3}^{C_3} & n_{f_3}^{C_3} & -1 & 0 & -1 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ l_{f_n}^{C_n} & m_{f_n}^{C_n} & n_{f_n}^{C_n} & -1 & 0 & -1 & 0 \end{bmatrix} A= lf1G1lf2G2lf3G3⋮lfnGnlf1C1lf2C2lf3C3⋮lfnCnmf1G1mf2G2mf3G3⋮mfnGnmf1C1mf2C2mf3C3⋮mfnCnnf1G1nf2G2nf3G3⋮nfnGnnf1C1nf2C2nf3C3⋮nfnCn−1−1−1⋮−1−1−1−1⋮−1000⋮0000⋮0000⋮0−1−1−1⋮−1000⋮0000⋮0
则状态更新为:
x k = [ x ^ k , 1 − x ^ k , 2 − x ^ k , 3 − ⋮ x ^ k , 7 − ] + K k ( [ z k , 1 z k , 2 z k , 3 ] − A [ x ^ k , 1 − x ^ k , 2 − x ^ k , 3 − ⋮ x ^ k , 7 − ] ) x_k = \begin{bmatrix} \hat{x}_{k,1}^- \\ \hat{x}_{k,2}^- \\ \hat{x}_{k,3}^- \\ \vdots \\ \hat{x}_{k,7}^- \end{bmatrix}+ K_k \left( \begin{bmatrix} z_{k,1} \\ z_{k,2} \\ z_{k,3} \end{bmatrix} - A \begin{bmatrix} \hat{x}_{k,1}^- \\ \hat{x}_{k,2}^- \\ \hat{x}_{k,3}^- \\ \vdots \\ \hat{x}_{k,7}^- \end{bmatrix} \right) xk= x^k,1−x^k,2−x^k,3−⋮x^k,7− +Kk zk,1zk,2zk,3 −A x^k,1−x^k,2−x^k,3−⋮x^k,7−
简化后:
x k = [ x ^ k , 1 − x ^ k , 2 − x ^ k , 3 − ⋮ x ^ k , 7 − ] + K k [ z k , 1 − ( A x ^ k − ) 1 z k , 2 − ( A x ^ k − ) 2 z k , 3 − ( A x ^ k − ) 3 ] x_k = \begin{bmatrix} \hat{x}_{k,1}^- \\ \hat{x}_{k,2}^- \\ \hat{x}_{k,3}^- \\ \vdots \\ \hat{x}_{k,7}^- \end{bmatrix}+ K_k \begin{bmatrix} z_{k,1} - (A \hat{x}_k^-)_{1} \\ z_{k,2} - (A \hat{x}_k^-)_{2} \\ z_{k,3} - (A \hat{x}_k^-)_{3} \end{bmatrix} xk= x^k,1−x^k,2−x^k,3−⋮x^k,7− +Kk zk,1−(Ax^k−)1zk,2−(Ax^k−)2zk,3−(Ax^k−)3 带入卡尔曼增益 K k K_k Kk 计算结果:
K k = [ C o v X X C o v X X + σ 1 2 0 0 0 C o v Y Y C o v Y Y + σ 2 2 0 0 0 C o v Z Z C o v Z Z + σ 3 2 0 0 0 0 0 0 0 0 0 0 0 0 ] K_k = \begin{bmatrix} \frac{Cov_{XX}}{Cov_{XX} + \sigma_1^2} & 0 & 0 \\ 0 & \frac{Cov_{YY}}{Cov_{YY} + \sigma_2^2} & 0 \\ 0 & 0 & \frac{Cov_{ZZ}}{Cov_{ZZ} + \sigma_3^2} \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} Kk= CovXX+σ12CovXX0000000CovYY+σ22CovYY0000000CovZZ+σ32CovZZ0000 最终状态更新为:
x k = [ x ^ k , 1 − x ^ k , 2 − x ^ k , 3 − ⋮ x ^ k , 7 − ] + [ C o v X X C o v X X + σ 1 2 0 0 0 C o v Y Y C o v Y Y + σ 2 2 0 0 0 C o v Z Z C o v Z Z + σ 3 2 0 0 0 0 0 0 0 0 0 0 0 0 ] [ z k , 1 − ( A x ^ k − ) 1 z k , 2 − ( A x ^ k − ) 2 z k , 3 − ( A x ^ k − ) 3 ] x_k = \begin{bmatrix} \hat{x}_{k,1}^- \\ \hat{x}_{k,2}^- \\ \hat{x}_{k,3}^- \\ \vdots \\ \hat{x}_{k,7}^- \end{bmatrix}+ \begin{bmatrix} \frac{Cov_{XX}}{Cov_{XX} + \sigma_1^2} & 0 & 0 \\ 0 & \frac{Cov_{YY}}{Cov_{YY} + \sigma_2^2} & 0 \\ 0 & 0 & \frac{Cov_{ZZ}}{Cov_{ZZ} + \sigma_3^2} \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} z_{k,1} - (A \hat{x}_k^-)_{1} \\ z_{k,2} - (A \hat{x}_k^-)_{2} \\ z_{k,3} - (A \hat{x}_k^-)_{3} \end{bmatrix} xk= x^k,1−x^k,2−x^k,3−⋮x^k,7− + CovXX+σ12CovXX0000000CovYY+σ22CovYY0000000CovZZ+σ32CovZZ0000 zk,1−(Ax^k−)1zk,2−(Ax^k−)2zk,3−(Ax^k−)3 -
更新误差协方差矩阵:
更新误差协方差矩阵 P k P_k Pk:P k = ( I − K k A ) P k − P_k = (I - K_k A) P_k^- Pk=(I−KkA)Pk−
带入计算:
假设 I I I 为单位矩阵:
I = [ 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 ] I = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} I= 1000000010000000100000001000000010000000100000001 卡尔曼增益 K k K_k Kk 为:
K k = [ C o v X X C o v X X + σ 1 2 0 0 0 C o v Y Y C o v Y Y + σ 2 2 0 0 0 C o v Z Z C o v Z Z + σ 3 2 0 0 0 0 0 0 0 0 0 0 0 0 ] K_k = \begin{bmatrix} \frac{Cov_{XX}}{Cov_{XX} + \sigma_1^2} & 0 & 0 \\ 0 & \frac{Cov_{YY}}{Cov_{YY} + \sigma_2^2} & 0 \\ 0 & 0 & \frac{Cov_{ZZ}}{Cov_{ZZ} + \sigma_3^2} \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} Kk= CovXX+σ12CovXX0000000CovYY+σ22CovYY0000000CovZZ+σ32CovZZ0000 假设观测矩阵 H H H 为设计矩阵 A A A:
A = [ l f 1 G 1 m f 1 G 1 n f 1 G 1 − 1 0 0 0 l f 2 G 2 m f 2 G 2 n f 2 G 2 − 1 0 0 0 l f 3 G 3 m f 3 G 3 n f 3 G 3 − 1 0 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ l f n G n m f n G n n f n G n − 1 0 0 0 l f 1 C 1 m f 1 C 1 n f 1 C 1 − 1 0 − 1 0 l f 2 C 2 m f 2 C 2 n f 2 C 2 − 1 0 − 1 0 l f 3 C 3 m f 3 C 3 n f 3 C 3 − 1 0 − 1 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ l f n C n m f n C n n f n C n − 1 0 − 1 0 ] A = \begin{bmatrix} l_{f_1}^{G_1} & m_{f_1}^{G_1} & n_{f_1}^{G_1} & -1 & 0 & 0 & 0 \\ l_{f_2}^{G_2} & m_{f_2}^{G_2} & n_{f_2}^{G_2} & -1 & 0 & 0 & 0 \\ l_{f_3}^{G_3} & m_{f_3}^{G_3} & n_{f_3}^{G_3} & -1 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ l_{f_n}^{G_n} & m_{f_n}^{G_n} & n_{f_n}^{G_n} & -1 & 0 & 0 & 0 \\ l_{f_1}^{C_1} & m_{f_1}^{C_1} & n_{f_1}^{C_1} & -1 & 0 & -1 & 0 \\ l_{f_2}^{C_2} & m_{f_2}^{C_2} & n_{f_2}^{C_2} & -1 & 0 & -1 & 0 \\ l_{f_3}^{C_3} & m_{f_3}^{C_3} & n_{f_3}^{C_3} & -1 & 0 & -1 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ l_{f_n}^{C_n} & m_{f_n}^{C_n} & n_{f_n}^{C_n} & -1 & 0 & -1 & 0 \end{bmatrix} A= lf1G1lf2G2lf3G3⋮lfnGnlf1C1lf2C2lf3C3⋮lfnCnmf1G1mf2G2mf3G3⋮mfnGnmf1C1mf2C2mf3C3⋮mfnCnnf1G1nf2G2nf3G3⋮nfnGnnf1C1nf2C2nf3C3⋮nfnCn−1−1−1⋮−1−1−1−1⋮−1000⋮0000⋮0000⋮0−1−1−1⋮−1000⋮0000⋮0 则更新误差协方差矩阵为:
P k = ( [ 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 ] − [ C o v X X C o v X X + σ 1 2 0 0 0 C o v Y Y C o v Y Y + σ 2 2 0 0 0 C o v Z Z C o v Z Z + σ 3 2 0 0 0 0 0 0 0 0 0 0 0 0 ] [ l f 1 G 1 m f 1 G 1 n f 1 G 1 − 1 0 0 0 l f 2 G 2 m f 2 G 2 n f 2 G 2 − 1 0 0 0 l f 3 G 3 m f 3 G 3 n f 3 G 3 − 1 0 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ l f n G n m f n G n n f n G n − 1 0 0 0 l f 1 C 1 m f 1 C 1 n f 1 C 1 − 1 0 − 1 0 l f 2 C 2 m f 2 C 2 n f 2 C 2 − 1 0 − 1 0 l f 3 C 3 m f 3 C 3 n f 3 C 3 − 1 0 − 1 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ l f n C n m f n C n n f n C n − 1 0 − 1 0 ] ) [ C o v X X 0 0 0 0 0 0 C o v Y Y 0 0 0 0 0 0 C o v Z Z 0 0 0 0 0 0 C o v δ t δ t 0 0 0 0 0 0 ∗ ∗ 0 0 0 0 ∗ ∗ ] P_k = \left( \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} - \begin{bmatrix} \frac{Cov_{XX}}{Cov_{XX} + \sigma_1^2} & 0 & 0 \\ 0 & \frac{Cov_{YY}}{Cov_{YY} + \sigma_2^2} & 0 \\ 0 & 0 & \frac{Cov_{ZZ}}{Cov_{ZZ} + \sigma_3^2} \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} l_{f_1}^{G_1} & m_{f_1}^{G_1} & n_{f_1}^{G_1} & -1 & 0 & 0 & 0 \\ l_{f_2}^{G_2} & m_{f_2}^{G_2} & n_{f_2}^{G_2} & -1 & 0 & 0 & 0 \\ l_{f_3}^{G_3} & m_{f_3}^{G_3} & n_{f_3}^{G_3} & -1 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ l_{f_n}^{G_n} & m_{f_n}^{G_n} & n_{f_n}^{G_n} & -1 & 0 & 0 & 0 \\ l_{f_1}^{C_1} & m_{f_1}^{C_1} & n_{f_1}^{C_1} & -1 & 0 & -1 & 0 \\ l_{f_2}^{C_2} & m_{f_2}^{C_2} & n_{f_2}^{C_2} & -1 & 0 & -1 & 0 \\ l_{f_3}^{C_3} & m_{f_3}^{C_3} & n_{f_3}^{C_3} & -1 & 0 & -1 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ l_{f_n}^{C_n} & m_{f_n}^{C_n} & n_{f_n}^{C_n} & -1 & 0 & -1 & 0 \end{bmatrix} \right) \begin{bmatrix} Cov_{XX} & 0 & 0 & 0 & 0 & 0 \\ 0 & Cov_{YY} & 0 & 0 & 0 & 0 \\ 0 & 0 & Cov_{ZZ} & 0 & 0 & 0 \\ 0 & 0 & 0 & Cov_{\delta t \delta t} & 0 & 0 \\ 0 & 0 & 0 & 0 & * & * \\ 0 & 0 & 0 & 0 & * & * \\ \end{bmatrix} Pk= 1000000010000000100000001000000010000000100000001 − CovXX+σ12CovXX0000000CovYY+σ22CovYY0000000CovZZ+σ32CovZZ0000 lf1G1lf2G2lf3G3⋮lfnGnlf1C1lf2C2lf3C3⋮lfnCnmf1G1mf2G2mf3G3⋮mfnGnmf1C1mf2C2mf3C3⋮mfnCnnf1G1nf2G2nf3G3⋮nfnGnnf1C1nf2C2nf3C3⋮nfnCn−1−1−1⋮−1−1−1−1⋮−1000⋮0000⋮0000⋮0−1−1−1⋮−1000⋮0000⋮0 CovXX000000CovYY000000CovZZ000000Covδtδt000000∗∗0000∗∗ 进一步计算得到:进一步计算得到:
P k = ( [ 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 ] − [ C o v X X C o v X X + σ 1 2 0 0 0 C o v Y Y C o v Y Y + σ 2 2 0 0 0 C o v Z Z C o v Z Z + σ 3 2 0 0 0 0 0 0 0 0 0 0 0 0 ] ) [ C o v X X 0 0 0 0 0 0 C o v Y Y 0 0 0 0 0 0 C o v Z Z 0 0 0 0 0 0 C o v δ t δ t 0 0 0 0 0 0 ∗ ∗ 0 0 0 0 ∗ ∗ ] P_k = \left( \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} - \begin{bmatrix} \frac{Cov_{XX}}{Cov_{XX} + \sigma_1^2} & 0 & 0 \\ 0 & \frac{Cov_{YY}}{Cov_{YY} + \sigma_2^2} & 0 \\ 0 & 0 & \frac{Cov_{ZZ}}{Cov_{ZZ} + \sigma_3^2} \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \right) \begin{bmatrix} Cov_{XX} & 0 & 0 & 0 & 0 & 0 \\ 0 & Cov_{YY} & 0 & 0 & 0 & 0 \\ 0 & 0 & Cov_{ZZ} & 0 & 0 & 0 \\ 0 & 0 & 0 & Cov_{\delta t \delta t} & 0 & 0 \\ 0 & 0 & 0 & 0 & * & * \\ 0 & 0 & 0 & 0 & * & * \\ \end{bmatrix} Pk= 1000000010000000100000001000000010000000100000001 − CovXX+σ12CovXX0000000CovYY+σ22CovYY0000000CovZZ+σ32CovZZ0000 CovXX000000CovYY000000CovZZ000000Covδtδt000000∗∗0000∗∗ 最终得到:
P k = [ ( 1 − C o v X X C o v X X + σ 1 2 ) C o v X X 0 0 0 0 0 0 ( 1 − C o v Y Y C o v Y Y + σ 2 2 ) C o v Y Y 0 0 0 0 0 0 ( 1 − C o v Z Z C o v Z Z + σ 3 2 ) C o v Z Z 0 0 0 0 0 0 C o v δ t δ t 0 0 0 0 0 0 ∗ ∗ 0 0 0 0 ∗ ∗ ] P_k = \begin{bmatrix} \left(1 - \frac{Cov_{XX}}{Cov_{XX} + \sigma_1^2}\right) Cov_{XX} & 0 & 0 & 0 & 0 & 0 \\ 0 & \left(1 - \frac{Cov_{YY}}{Cov_{YY} + \sigma_2^2}\right) Cov_{YY} & 0 & 0 & 0 & 0 \\ 0 & 0 & \left(1 - \frac{Cov_{ZZ}}{Cov_{ZZ} + \sigma_3^2}\right) Cov_{ZZ} & 0 & 0 & 0 \\ 0 & 0 & 0 & Cov_{\delta t \delta t} & 0 & 0 \\ 0 & 0 & 0 & 0 & * & * \\ 0 & 0 & 0 & 0 & * & * \\ \end{bmatrix} Pk= (1−CovXX+σ12CovXX)CovXX000000(1−CovYY+σ22CovYY)CovYY000000(1−CovZZ+σ32CovZZ)CovZZ000000Covδtδt000000∗∗0000∗∗
16.2 站星双差Kalman滤波伪距差分定位流程
站星双差仅有位置状态量,所以其Kalman滤波流程更加简单。
对于时间更新步骤,基本就使用单点结果对概略位置进行填充,所以实际上已经降级为最小二乘,因为前后历元状态量在时间序列上不存在相关性。
但对于观测更新过程,观测值的方差需要考虑因星间作差引入的相关性。
对于没有做星间单差之前
V u d = [ p 1 p 2 p 3 p 4 ] R u d = [ σ 1 2 0 0 0 0 σ 2 2 0 0 0 0 σ 3 2 0 0 0 0 σ 4 2 ] V_{ud} = \begin{bmatrix} p^1 \\ p^2 \\ p^3 \\ p^4 \end{bmatrix} \quad R_{ud} = \begin{bmatrix} \sigma_1^2 & 0 & 0 & 0 \\ 0 & \sigma_2^2 & 0 & 0 \\ 0 & 0 & \sigma_3^2 & 0 \\ 0 & 0 & 0 & \sigma_4^2 \end{bmatrix} Vud= p1p2p3p4 Rud= σ120000σ220000σ320000σ42
星间单差之后
V s d = [ p 2 − p 1 p 3 − p 1 p 4 − p 1 ] R s d = [ σ 2 2 + σ 1 2 σ 2 2 + σ 1 2 σ 2 2 + σ 1 2 σ 1 2 + σ 3 2 σ 1 2 + σ 3 2 σ 1 2 + σ 3 2 σ 1 2 + σ 4 2 σ 1 2 + σ 4 2 σ 1 2 + σ 4 2 ] V_{sd} = \begin{bmatrix} p^2 - p^1 \\ p^3 - p^1 \\ p^4 - p^1 \end{bmatrix} \quad R_{sd} = \begin{bmatrix} \sigma_2^2 + \sigma_1^2 & \sigma_2^2 + \sigma_1^2 & \sigma_2^2 + \sigma_1^2 \\ \sigma_1^2 + \sigma_3^2 & \sigma_1^2 + \sigma_3^2 & \sigma_1^2 + \sigma_3^2 \\ \sigma_1^2 + \sigma_4^2 & \sigma_1^2 + \sigma_4^2 & \sigma_1^2 + \sigma_4^2 \end{bmatrix} Vsd= p2−p1p3−p1p4−p1 Rsd= σ22+σ12σ12+σ32σ12+σ42σ22+σ12σ12+σ32σ12+σ42σ22+σ12σ12+σ32σ12+σ42
其余流程相同,不再推导。
相关文章:

让GNSSRTK不再难【第二天-第7部分2】
状态更新计算过程: 计算卡尔曼增益: 根据预测的误差协方差矩阵 P k − P_k^- Pk− 和观测噪声协方差矩阵 R R R 计算卡尔曼增益 K k K_k Kk: K k P k − H T ( H P k − H T R ) − 1 K_k P_k^- H^T (H P_k^- H^T R)^{-1} KkPk…...

计算引擎:Flink核心概念
Apache Flink 是一个流处理框架,擅长处理实时数据流和批处理任务。Flink 提供了强大的功能来处理和分析大量数据。以下是 Flink 的核心概念: 1. DataStream 和 DataSet API DataStream API: 用于处理无界数据流,即不断生成和流动的数据。例如,传感器数据、日志等。DataSet…...
技术前沿 |【大模型InstructBLIP进行指令微调】
大模型InstructBLIP进行指令微调 一、引言二、InstructBLIP模型介绍三、指令微调训练通用视觉语言模型的应用潜力四、InstructBLIP的指令微调训练步骤五、实验结果与讨论六、结论与展望 一、引言 随着人工智能技术的快速发展,视觉语言模型(Vision-Langu…...

CSS-布局-flex
CSS3 新增了弹性盒子模型( Flexible Box 或 FlexBox ),是一种新的用于在 HTML 页面实现布局的方式。使得 HTML 页面适应不同尺寸的屏幕和不同的设备时,元素是可预测地运行。 基本概念 容器:使用 display:flex 或 display:inline-flex 声明的…...

「C系列」C 数组
文章目录 一、C 数组1. 声明数组2. 初始化数组3. 访问数组元素4. 数组越界5. 多维数组 二、C 操作数组的方法有哪些三、C 数组-应用场景1. 存储固定数量的数据2. 实现算法(如排序)3. 处理数据集合 四、相关链接 一、C 数组 在C语言中,数组是…...

Python框架scrapy有什么天赋异禀
Scrapy框架与一般的爬虫代码之间有几个显著的区别,这些差异主要体现在设计模式、代码结构、执行效率以及可扩展性等方面。下面是一些关键的不同点: 结构化与模块化: Scrapy:提供了高度结构化的框架,包括定义好的Spider…...

【ROS2大白话】四、ROS2非常简单的传参方式
系列文章目录 【ROS2大白话】一、ROS2 humble及cartorgrapher安装 【ROS2大白话】二、turtlebot3安装 【ROS2大白话】三、给turtlebot3安装realsense深度相机 【ROS2大白话】四、ROS2非常简单的传参方式 文章目录 系列文章目录前言一、launch文件传参的demo1. 编写launch.py文…...

浅谈mysql 的批量delete 和 使用in条件批量删除问题
在考虑这两个DELETE语句的性能时,我们需要考虑数据库如何执行这些查询以及它们背后可能涉及的索引和数据结构。 1.执行多个单独的DELETE语句: DELETE FROM a WHERE b 1 AND c 1; ... DELETE FROM a WHERE b 1000 AND c 1000; 这种方法的优点是每…...

【Spring Boot】过滤敏感词的两种实现
文章目录 项目场景前置知识前缀树 实现方式解决方案一:读取敏感词文件生成前缀树构建敏感词过滤器1. 导入敏感词文件 src/main/resources/sensitive_words.txt2. 构建敏感词过滤器 SensitiveFilter3. 测试与使用 解决方案二:使用第三方插件 houbb/sensit…...
吗)
在 Zustand 中管理状态能使用类(Class)吗
在 Zustand 中,通常不推荐使用类(Class)来管理状态,因为 Zustand 的设计理念是基于函数式编程和 React Hooks 的。然而,仍然可以在 Zustand 中间接地使用类,但这并不是 Zustand 的典型用法。 如果确实想要…...

MoreTable 方法selectWithFun,count 使用实例
ORM Bee, example for MoreTable methods:selectWithFun,count ORM Bee时, MoreTable 方法selectWithFun,count 使用实例 package org.teasoft.exam.bee.osql;import org.teasoft.bee.osql.BeeException; import org.teasoft.bee.osql.FunctionType; import org.teasoft.be…...

【SpringBoot】在Spring中使用自定义条件类在Java声明Bean时实现条件注入
在Spring框架中,通过实现org.springframework.context.annotation.Condition接口并重写matches()方法,可以根据自定义条件来控制Bean的注入。这种机制非常灵活,可以帮助开发人员根据环境或配置来有选择地启用或禁用某些Bean。本文将详细介绍如…...

网卡聚合链路配置
创建名为mybond0的绑定,使用示例如下: # nmcli con add type bond con-name mybond0 ifname mybond0 mode active-backup添加从属接口,使用示例如下: # nmcli con add type bond-slave ifname enp3s0 master mybond0要添加其他从…...
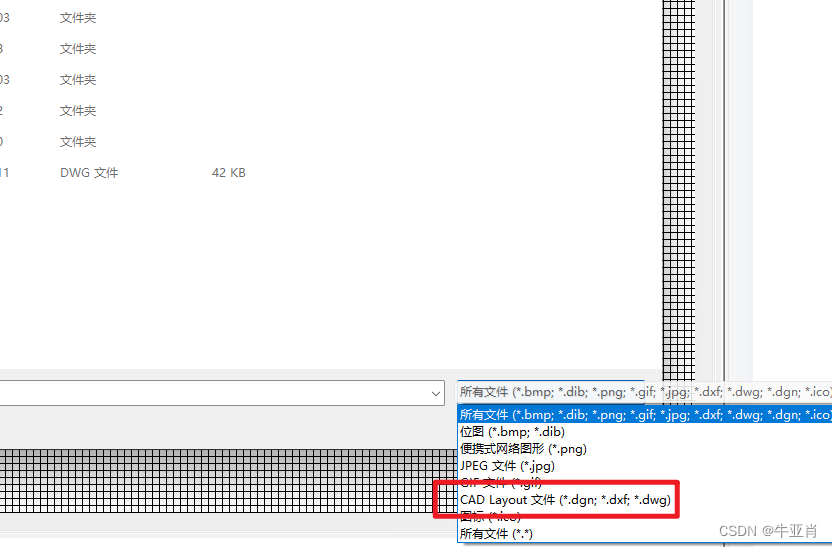
PlantSimulation导入cad图作为背景
PlantSimulation导入cad图作为背景 首先要整理cad文件,正常的工艺规划总图中存在较多杂乱文件,这些信息是不需要的,如果直接导入,会非常卡。 1、打开cad软件,使用layon命令打开所有的隐藏图层,删除不需要…...

【大模型】个人对大模型选择的见解
选择大模型产品时,需要考虑多个因素,包括但不限于以下几点: 需求匹配度:首先,要明确你的需求是什么。不同的大模型产品可能在功能、性能、应用场景等方面有所侧重。例如,有的模型擅长自然语言处理ÿ…...

java的反射和python的鸭子类型
Java的反射(Reflection)和Python的鸭子类型(Duck Typing)感觉相似但又说不出具体的细节,本文借助kimi试图给出总结。 相似之处: 动态性:Java的反射允许程序在运行时查询、创建和修改类和对象的…...
爬虫工具yt-dlp
yt-dlp是youtube-dlp的一个fork,youtube-dlp曾经也较为活跃,但后来被众多网站屏蔽,于是大家转而在其基础上开发yt-dlp。yt-dlp的github项目地址为:GitHub - yt-dlp/yt-dlp: A feature-rich command-line audio/video downloaderA …...

【代码随想录训练营】【Day 50】【动态规划-9】| Leetcode 198, 213, 337
【代码随想录训练营】【Day 50】【动态规划-9】【需二刷】| Leetcode 198, 213, 337 需强化知识点 需二刷,打家劫舍系列 题目 198. 打家劫舍 class Solution:def rob(self, nums: List[int]) -> int:if len(nums) 1:return nums[0]dp [0] * (len(nums))dp…...
)
源码讲解kafka 如何使用零拷贝技术(zero-copy)
前言 kafka 作为一个高吞吐量的分布式消息系统,广泛应用与实时应用场景中。为了实现高效的数据传输,kafka使用了零拷贝技术(zero-copy)显著提高了性能。本文将详细讲解 Kafka 如何利用零拷贝技术优化数据传输。 什么是零拷贝 零拷贝技术目的是减少数据传输的效率。在传统…...

Ubuntu20.04配置qwen0.5B记录
环境简介 Ubuntu20.04、 NVIDIA-SMI 545.29.06、 Cuda 11.4、 python3.10、 pytorch1.11.0 开始搭建 python环境设置 创建虚拟环境 conda create --name qewn python3.10预安装modelscope和transformers pip install modelscope pip install transformers安装pytorch co…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
