AVL树 ---(C++)
本篇讲全面的讲解 AVL 树的插入,旋转以及验证 AVL 树的性能(本篇未实现删除代码)。至于为什么会有 AVL 树,这是因为简单的二叉搜索树并不能直接的保证搜索的效率,因为当我们在二叉搜索树中插入一段有序的序列的时候,二叉搜索树就会退化为单枝树,这个时候进行搜索的时候,时间复杂度就变为了 O(n^2),如下:
但是通过 AVL 树的旋转就可以很好的解决这个问题,使树近似等于完全二叉树或者满二叉树。
AVL 树代码
先给出代码,接着在下文中给出解释:
#pragma once #include <iostream> #include <assert.h>using namespace std;template <class K, class V> struct AVLTreeNode {AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;pair<K, V> _kv;int _balanceFactor;AVLTreeNode(const pair<K, V>& kv): _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _balanceFactor(0){} };template <class K, class V> class AVLTree { public:typedef AVLTreeNode<K, V> Node;Node* find(const K& key) {Node* cur = _root;while (cur) {if (cur->_kv.first < key)cur = cur->_right;else if (cur->_kv.first > key)cur = cur->_left;elsereturn cur;}return nullptr;}// 插入删除查找遍历bool insert(const pair<K, V>& kv) {if (_root == nullptr) {_root = new Node(kv);return true;}// 开始查找Node* parent = nullptr;Node* cur = _root;while (cur) {if (cur->_kv.first < kv.first)parent = cur, cur = cur->_right;else if (cur->_kv.first > kv.first)parent = cur, cur = cur->_left;elsereturn false;}// cur == nullptrcur = new Node(kv);//if (parent->_left == cur)// parent->_left = cur;//else// parent->_right = cur;if (parent->_kv.first > kv.first)parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;// 需要更新平衡因子// 如果是在父亲的左边,父亲的平衡因子减一、右边加一if (parent->_left == cur)parent->_balanceFactor--;elseparent->_balanceFactor++;// 查看爷爷结点是否需要更新while (parent) {if (parent->_balanceFactor == 0) {break;}else if (parent->_balanceFactor == 1 || parent->_balanceFactor == -1) {if (parent == _root)break;// 现在的parent就不可能等于nullparent = parent->_parent;cur = cur->_parent;if (parent->_left == cur)parent->_balanceFactor--;elseparent->_balanceFactor++;}else if(parent->_balanceFactor == 2 || parent->_balanceFactor == -2) {if (parent->_balanceFactor == 2 && cur->_balanceFactor == 1)RotateLeft(parent);else if (parent->_balanceFactor == -2 && cur->_balanceFactor == -1)RotateRight(parent);else if (parent->_balanceFactor == -2 && cur->_balanceFactor == 1)RotateLeftRight(parent);else if (parent->_balanceFactor == 2 && cur->_balanceFactor == -1)RotateRightLeft(parent);elseassert(false);break;}else {assert(false);}}return true;}void RotateRight(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;// 将左孩子的右节点链接到原父亲结点if (subLR) subLR->_parent = parent;parent->_left = subLR;Node* ppNode = parent->_parent;// 将左孩子变为原父亲结点的父亲subL->_right = parent;parent->_parent = subL;// 将爷爷结点重新链接if (ppNode == nullptr) {_root = subL;_root->_parent = nullptr;}else {if (ppNode->_left == parent)ppNode->_left = subL;elseppNode->_right = subL;subL->_parent = ppNode;}subL->_balanceFactor = parent->_balanceFactor = 0;}void RotateLeft(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;Node* ppNode = parent->_parent;parent->_right = subRL;if (subRL) subRL->_parent = parent;subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr) {_root = subR;_root->_parent = nullptr;}else {if (ppNode->_left == parent)ppNode->_left = subR;elseppNode->_right = subR;subR->_parent = ppNode;}subR->_balanceFactor = parent->_balanceFactor = 0;}void RotateRightLeft(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;int balanceFactor = subRL->_balanceFactor;RotateRight(subR);RotateLeft(parent);// 更新平衡因子subRL->_balanceFactor = 0;if (balanceFactor == -1) {parent->_balanceFactor = 0;subR->_balanceFactor = 1;}else if (balanceFactor == 1) {parent->_balanceFactor = -1;subR->_balanceFactor = 0;}else if (balanceFactor == 0) {parent->_balanceFactor = 0;subR->_balanceFactor = 0;}else {assert(false);}}void RotateLeftRight(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;int balanceFactor = subLR->_balanceFactor;// 先左旋后右旋RotateLeft(subL);RotateRight(parent);subLR->_balanceFactor = 0;if (balanceFactor == -1) {subL->_balanceFactor = 0;parent->_balanceFactor = 1;}else if (balanceFactor == 1) {parent->_balanceFactor = 0;subL->_balanceFactor = -1;}else if (balanceFactor == 0) {parent->_balanceFactor = 0;subL->_balanceFactor = 0;}else {assert(false);}}void InOrder() {_InOrder(_root);cout << endl;}int height() {int h = _height(_root);return h;}int size() {int s = _size(_root);return s;}bool IsBalance() {return _IsBalance(_root);}private:bool _IsBalance(Node* root) {if (root == nullptr)return true;int leftHeight = _height(root->_left);int rightHeight = _height(root->_right);if (abs(leftHeight - rightHeight) >= 2)return false;if (abs(root->_balanceFactor) >= 2)return false;return _IsBalance(root->_left) && _IsBalance(root->_right);}int _height(Node* root) {if (root == nullptr)return 0;int left = _height(root->_left);int right = _height(root->_right);int height = max(left, right);return height + 1;}int _size(Node* root) {if (root == nullptr)return 0;return _size(root->_left) + _size(root->_right) + 1;}void _InOrder(Node* root) {if (root == nullptr) return;_InOrder(root->_left);cout << root->_kv.first << " " << root->_kv.second << endl;_InOrder(root->_right);} private:Node* _root = nullptr; };
AVL 树的概念于抽象数据结构
一颗 AVL 树是空树或者是具有以下性质的二叉搜索树:
1. 它的左右子树都是 AVL 树
2. 左右子树的高度之差(平衡因子)的绝对值不超过 1
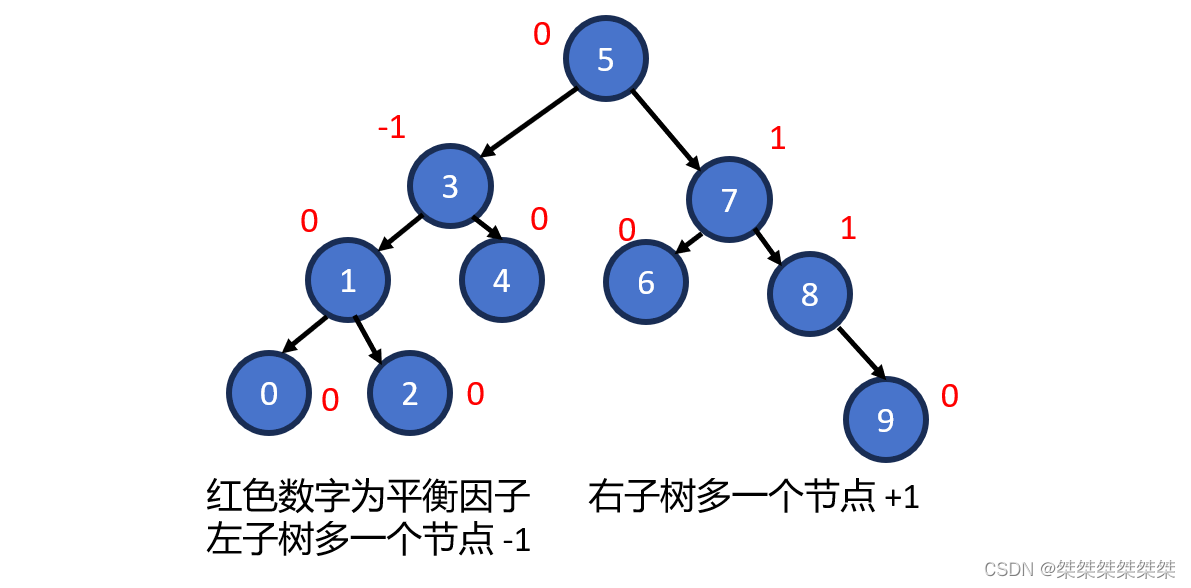
左右子树的高度差不超过 1,可以降低树的高度,减少平均搜索长度。如下:
关于 AVL 树的抽象数据结构,我们首先需要抽象出 AVL 树节点的数据结构,在 AVL 树中,我们存储的关键数据为键值对 pair,AVL 树节点中的平衡因子。然后需要一个指向左子树的指针,指向右子树的指针同时还需要一个指向父节点的指针,可以让我们便于更新每个节点的平衡因子。如下:
template <class K, class V> struct AVLTreeNode {AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;pair<K, V> _kv;int _balanceFactor;AVLTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _balanceFactor(0){} };
AVL 树的插入
关于 AVL 树而言,只是在二叉搜索树的基础上引入了平衡因子,所以 AVL 树也可以看出二叉搜索树(左右高度差不大于1的二叉搜索树),所以对于 AVL 树的插入,可以分为以下两步:
1. 按照二叉搜索树的方式插入新节点。
2. 调整节点的平衡因子。
所以我们插入节点,只需要找到应该插入的位置,然后插入即可,寻找插入位置按照:键值小于当前节点,向左子树搜索,键值大于当前节点,向右子树搜索的原则,直到找到空节点为止,就是应该插入的位置。寻找的时候,还需要记录下每一次搜索的父节点,便于链接指针,如下:
bool insert(const pair<K, V>& kv) {if (_root == nullptr) {_root = new Node(kv);return true;}// 开始查找Node* parent = nullptr;Node* cur = _root;while (cur) {if (cur->_kv.first < kv.first)parent = cur, cur = cur->_right;else if (cur->_kv.first > kv.first)parent = cur, cur = cur->_left;elsereturn false;}// cur == nullptrcur = new Node(kv);// 链接孩子节点和父节点if (parent->_kv.first > kv.first)parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;// 需要更新平衡因子...return true; }插入成功,则返回 true,插入失败(树中已经存在键值)则返回 false。
以上只是完成了插入,插入元素之后,我们还需要更新节点的平衡因子,更新平衡因子按照以下原则进行更新:
1. 插入元素位置位于父节点的右边,父节点的平衡因子 +1;
2. 插入元素位置位于父节点的左边,父节点的平衡因子 -1。
3. 更新完父节点的平衡因子之后,父节点的平衡因子的取值可能为 0、正负1、正负2。
5. 父节点的平衡因子更新完之后为0,不会影响父节点的父节点的平衡,所以不用在往上更新。
6. 父节点的平衡因子跟新完之后为正负1,说明原来父节点的平衡因子为0,这时还会影响父节点的父节点的平衡因子,所以需要继续向上更新。当某个节点的平衡原则为正负二的时候,我们就需要通过选择使树平衡。
如下:
// 需要更新平衡因子 // 如果是在父亲的左边,父亲的平衡因子减一、右边加一 if (parent->_left == cur)parent->_balanceFactor--; elseparent->_balanceFactor++; // 查看爷爷结点是否需要更新while (parent) {if (parent->_balanceFactor == 0) {break;}else if (parent->_balanceFactor == 1 || parent->_balanceFactor == -1) {if (parent == _root)break;// 现在的parent就不可能等于nullparent = parent->_parent;cur = cur->_parent;if (parent->_left == cur)parent->_balanceFactor--;elseparent->_balanceFactor++;}else if(parent->_balanceFactor == 2 || parent->_balanceFactor == -2) {if (parent->_balanceFactor == 2 && cur->_balanceFactor == 1)RotateLeft(parent);else if (parent->_balanceFactor == -2 && cur->_balanceFactor == -1)RotateRight(parent);else if (parent->_balanceFactor == -2 && cur->_balanceFactor == 1)RotateLeftRight(parent);else if (parent->_balanceFactor == 2 && cur->_balanceFactor == -1)RotateRightLeft(parent);elseassert(false);break;}else {assert(false);} }对于如上的代码中,其中最难的一步就是旋转,关于旋转一共会出现四种情况:左单旋、右单旋、左右双旋、右左双旋。
AVL 树的旋转
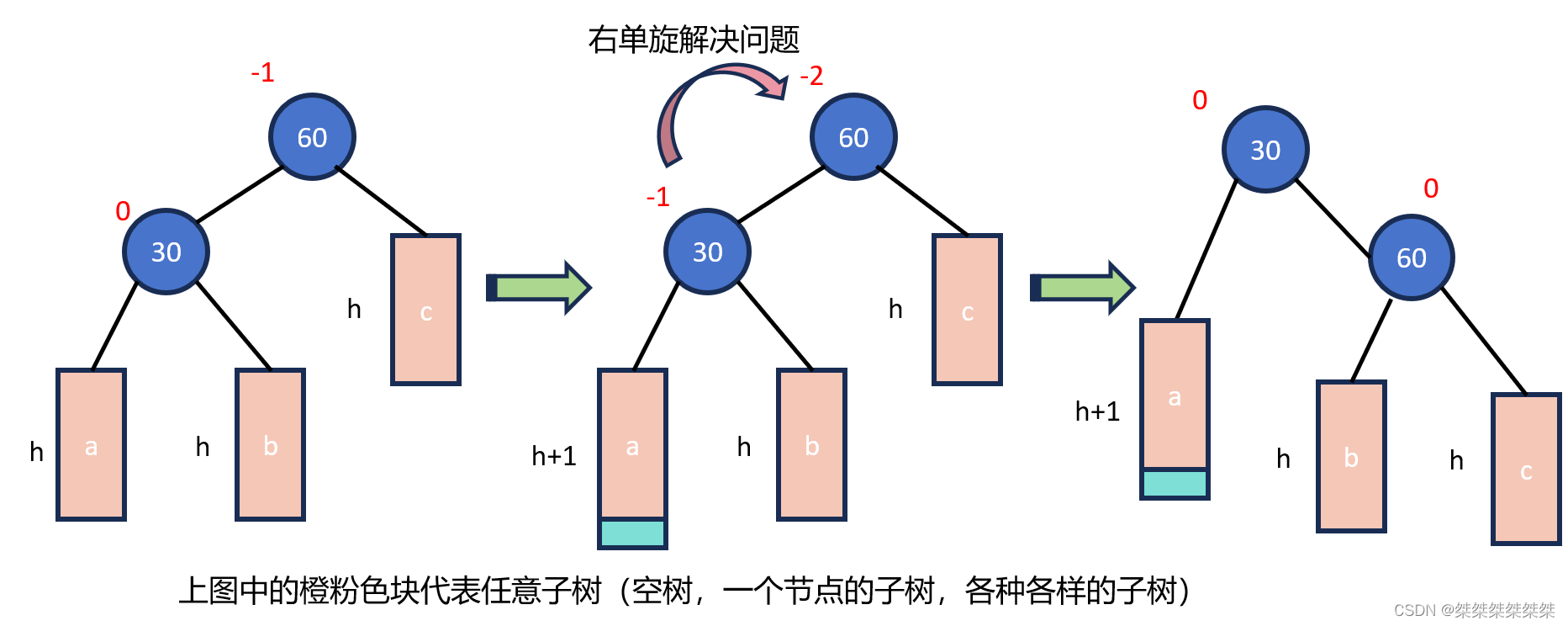
我们首先介绍右单旋,当新节点插入导较高左子树的左侧就会出现右单旋,关于右单旋出现的情况如下:
当出现如上所示的情况时(父亲节点的平衡因子等于-2,左孩子节点的平衡因子为-1时),我们就需要进行右旋,也就是将左孩子作为父节点,父节点作为右孩子,在将左孩子的右节点链接到原父节点上。其中还有需要注意的点:右旋时的父节点不一定是根节点,所以我们在旋转的时候,还需要记录下父节点的父节点,最后将其链接到一起。
void RotateRight(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;// 将左孩子的右节点链接到原父亲结点if (subLR) subLR->_parent = parent;parent->_left = subLR;Node* ppNode = parent->_parent;// 将左孩子变为原父亲结点的父亲subL->_right = parent;parent->_parent = subL;// 将爷爷结点重新链接if (ppNode == nullptr) {_root = subL;_root->_parent = nullptr;}else {if (ppNode->_left == parent)ppNode->_left = subL;elseppNode->_right = subL;subL->_parent = ppNode;}subL->_balanceFactor = parent->_balanceFactor = 0; }记得最后将节点的平衡因子设置为0。
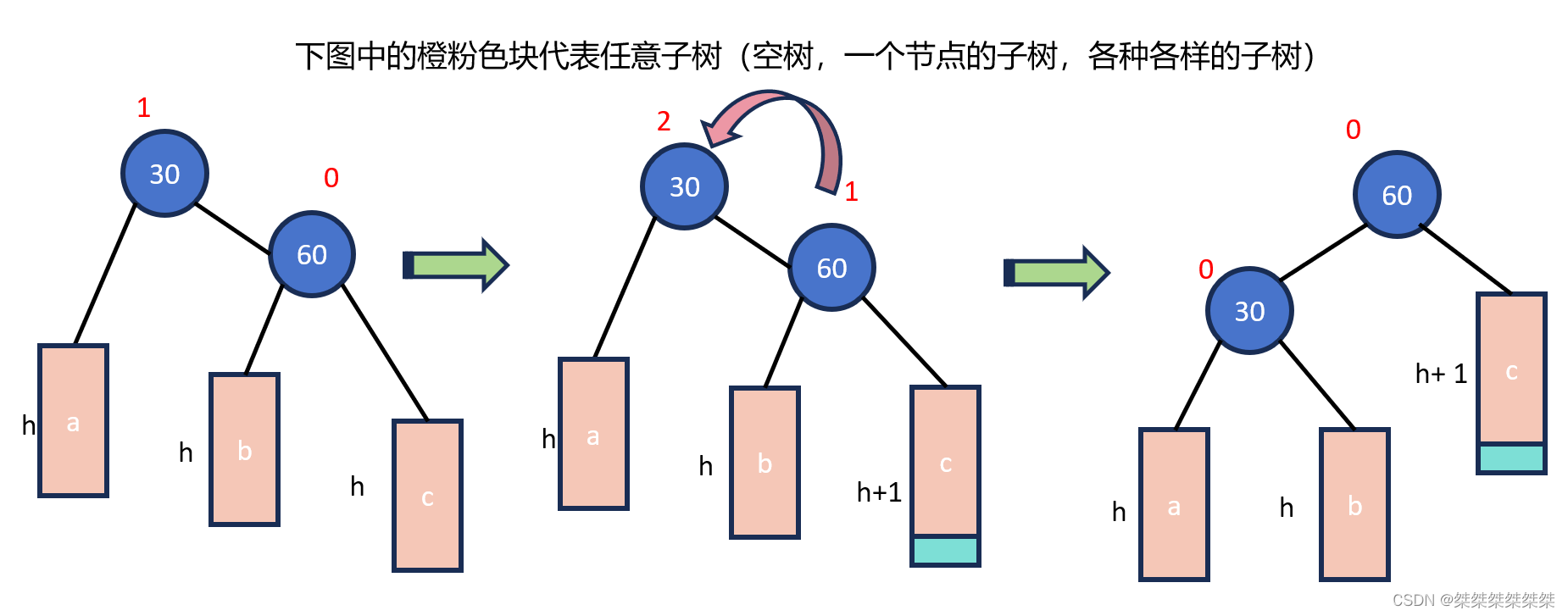
接着我们介绍左单旋:当新节点插入到较高右子树的右侧,关于这种情况如下:
关于左单旋,其思想和右单旋基本一致,不过是将右单旋的给镜像了过来。所以当父节点的平衡因子为2,右节点的平衡因子为1的时候,我们就需要对树进行左单旋。也就是让右孩子的左节点作为父节点的右孩子,左节点作为父节点,原父节点作为左孩子的左节点。注意原父节点的父节点是否为 nullptr,最后需要更新节点的平衡因子。如下:
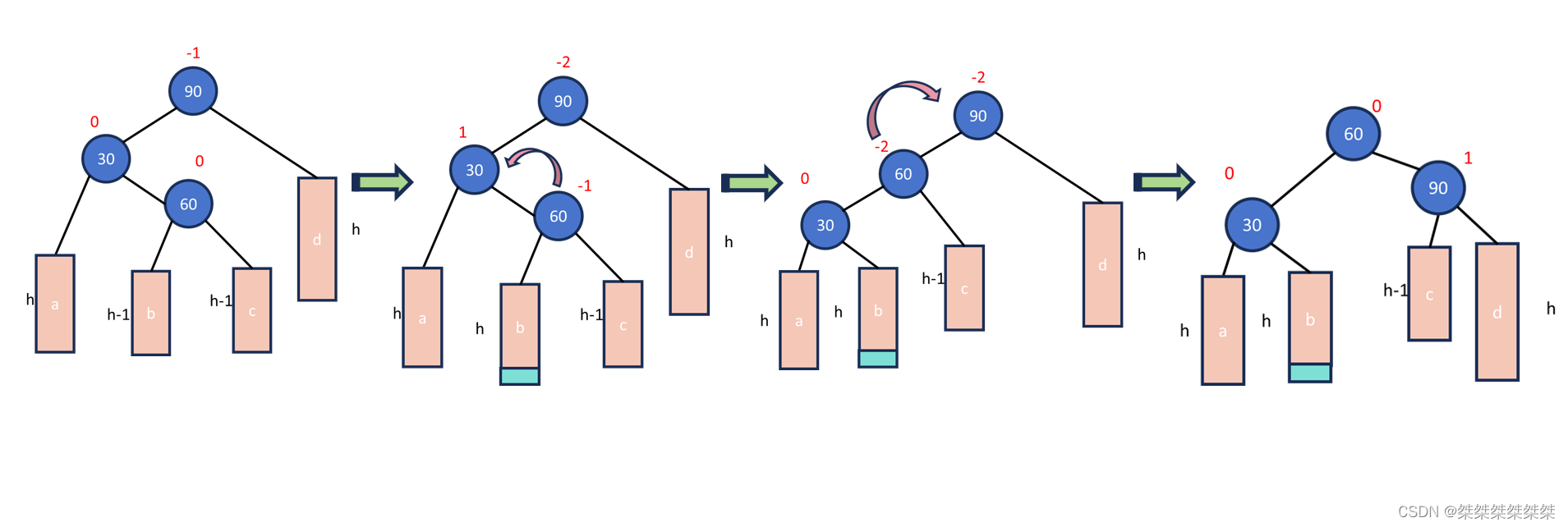
void RotateLeft(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;Node* ppNode = parent->_parent;parent->_right = subRL;if (subRL) subRL->_parent = parent;subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr) {_root = subR;_root->_parent = nullptr;}else {if (ppNode->_left == parent)ppNode->_left = subR;elseppNode->_right = subR;subR->_parent = ppNode;}subR->_balanceFactor = parent->_balanceFactor = 0; }第三种情况,左右双旋。左右双旋就是分别需要左旋一次,然后右旋一次,接着更新我们的平衡因子,如下:
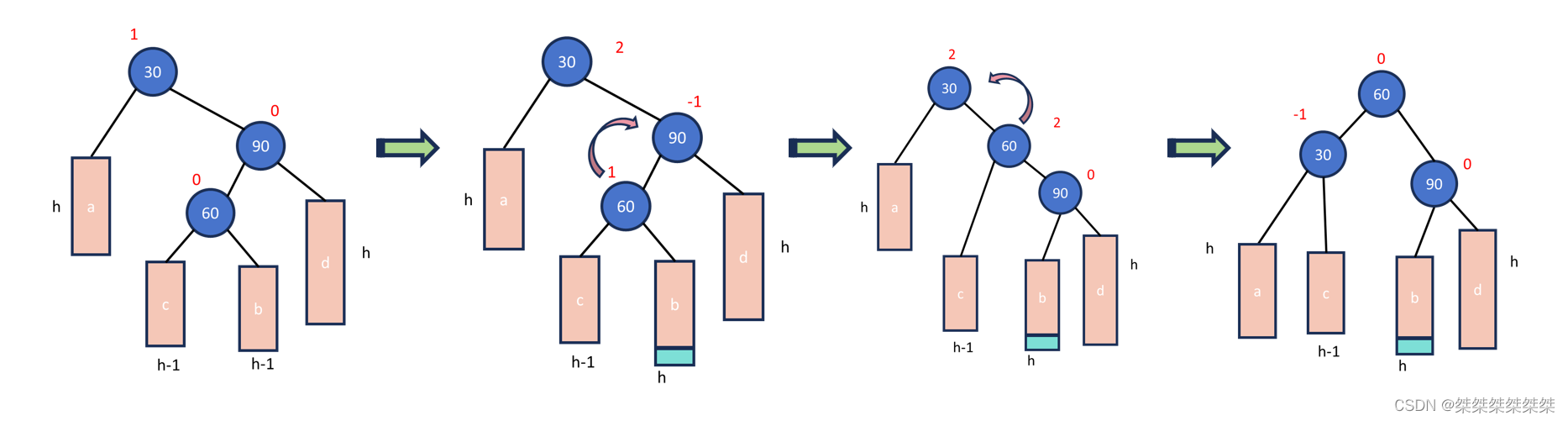
如上图所示,当左孩子节点的平衡因子为1,父节点的平衡因子为-2的时候,我们就需要进行左右双旋,当我们旋转之后,当前父节点的平衡因子一定为0,但原父节点和左孩子节点的平衡因子一共有三种情况,分别是0 0,1 0,0 -1。当 h = 0 的时候,插入的节点就是以上的60节点,旋转之后所有节点(一共就3个节点)都是为0,当节点插入到60的左边,那么30的平衡因子为0(如图),当节点插入到60的右边,90的平衡因子则为0。
因为在单独调用左单选,右单旋之后,会将所有节点的平衡因子都置为0,所以我们需要进行特殊处理。如下:
void RotateLeftRight(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;int balanceFactor = subLR->_balanceFactor;// 先左旋后右旋RotateLeft(subL);RotateRight(parent);subLR->_balanceFactor = 0;if (balanceFactor == -1) {subL->_balanceFactor = 0;parent->_balanceFactor = 1;}else if (balanceFactor == 1) {parent->_balanceFactor = 0;subL->_balanceFactor = -1;}else if (balanceFactor == 0) {parent->_balanceFactor = 0;subL->_balanceFactor = 0;}else {assert(false);} }最后一种情况:右左双旋。也就是先右旋然后在左旋,也就是和以上的情况是堆成的情况,如下:
对于需要右左旋转的情况为父节点为2,右孩子为1.关于转换的细节和以上的左右双旋的情况向对称,在这就不细讲了,代码如下:
void RotateRightLeft(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;int balanceFactor = subRL->_balanceFactor;RotateRight(subR);RotateLeft(parent);// 更新平衡因子subRL->_balanceFactor = 0;if (balanceFactor == -1) {parent->_balanceFactor = 0;subR->_balanceFactor = 1;}else if (balanceFactor == 1) {parent->_balanceFactor = -1;subR->_balanceFactor = 0;}else if (balanceFactor == 0) {parent->_balanceFactor = 0;subR->_balanceFactor = 0;}else {assert(false);} }
AVL 树的验证 + 测试
接下来我们将对我们是新的 AVL 树进行验证,也就是看我们写出的代码是否符合 AVL 树的特性,其中主要包括特性测试和压力测试。在进行测试之前,我们需要先写出一些辅助函数,如下:
template <class K, class V> class AVLTree { public:typedef AVLTreeNode<K, V> Node;void InOrder() {_InOrder(_root);cout << endl;}int height() {int h = _height(_root);return h;}int size() {int s = _size(_root);return s;}bool IsBalance() {return _IsBalance(_root);}private:bool _IsBalance(Node* root) {if (root == nullptr)return true;int leftHeight = _height(root->_left);int rightHeight = _height(root->_right);if (abs(leftHeight - rightHeight) >= 2)return false;if (abs(root->_balanceFactor) >= 2)return false;return _IsBalance(root->_left) && _IsBalance(root->_right);}int _height(Node* root) {if (root == nullptr)return 0;int left = _height(root->_left);int right = _height(root->_right);int height = max(left, right);return height + 1;}int _size(Node* root) {if (root == nullptr)return 0;return _size(root->_left) + _size(root->_right) + 1;}void _InOrder(Node* root) {if (root == nullptr) return;_InOrder(root->_left);cout << root->_kv.first << " " << root->_kv.second << endl;_InOrder(root->_right);} private:Node* _root = nullptr; };我们先进行特性测试,如下:
如上所示,我们一共验证了两组数据,其中包含了左旋、右旋、左右双旋、右左双旋四种情况。
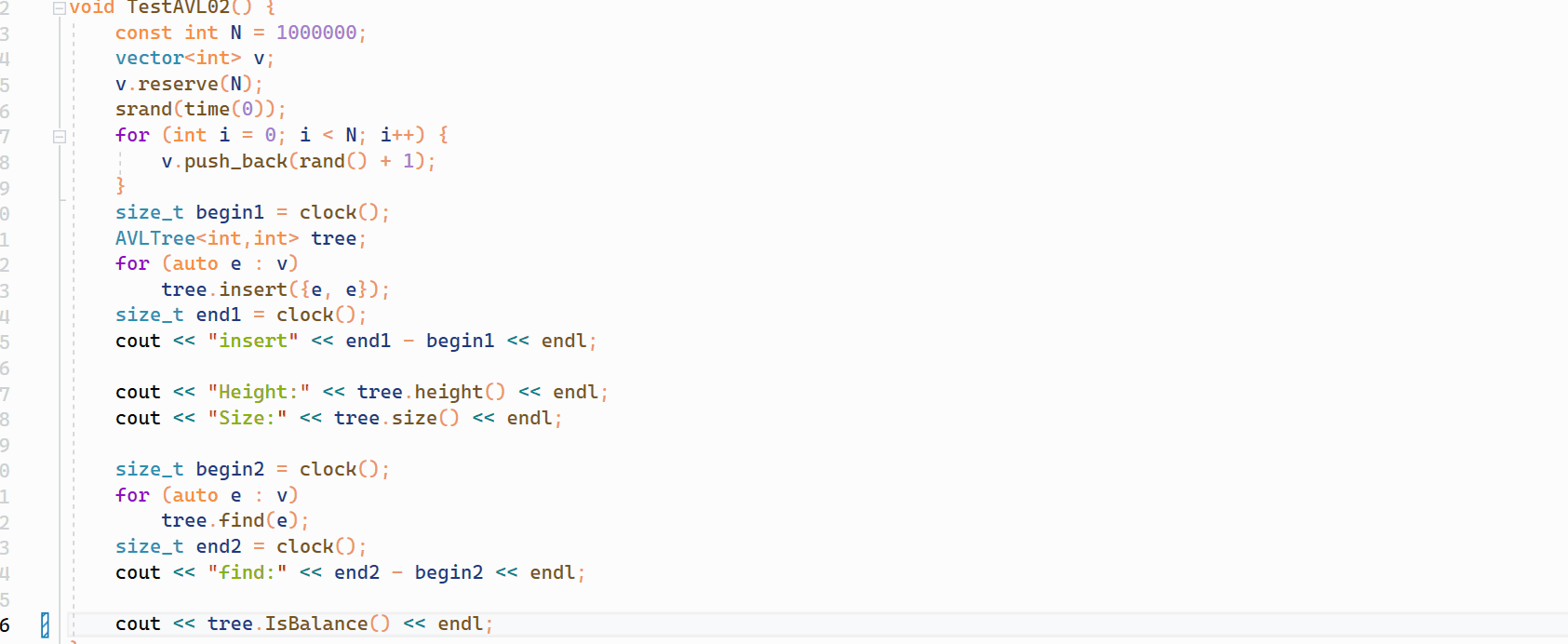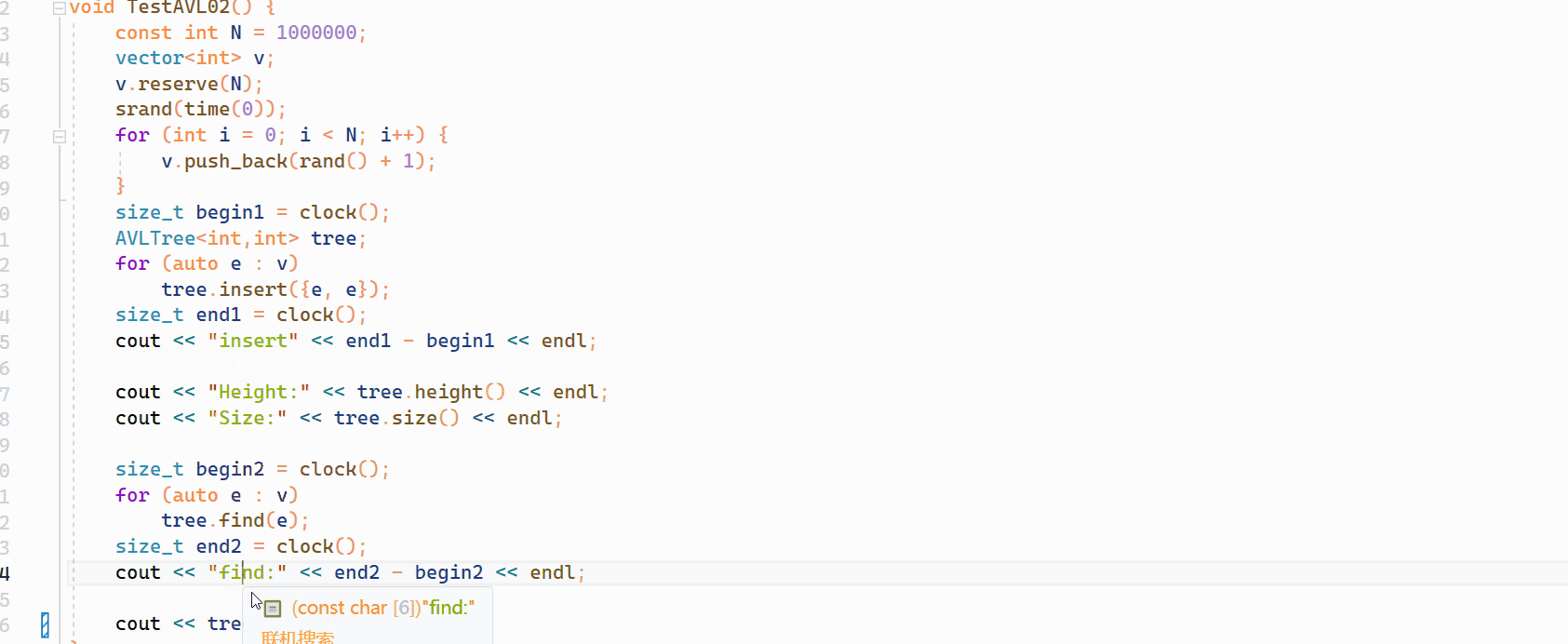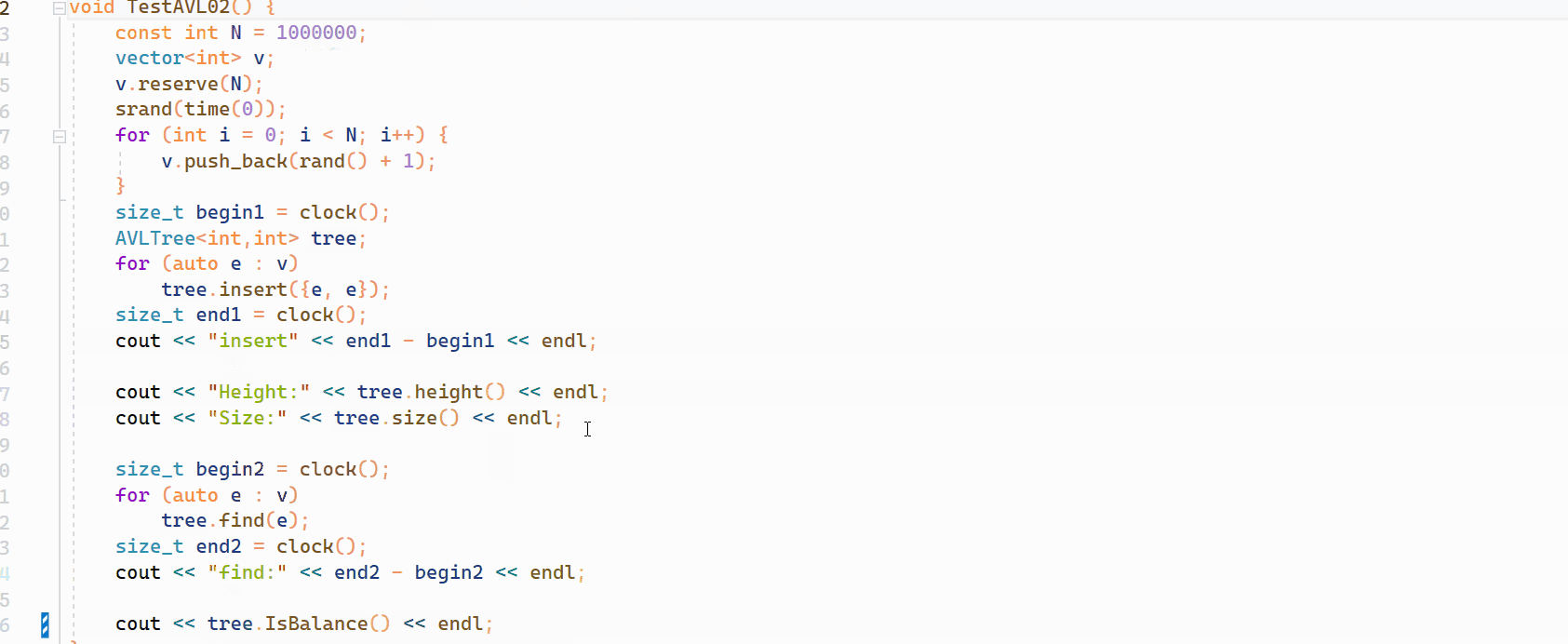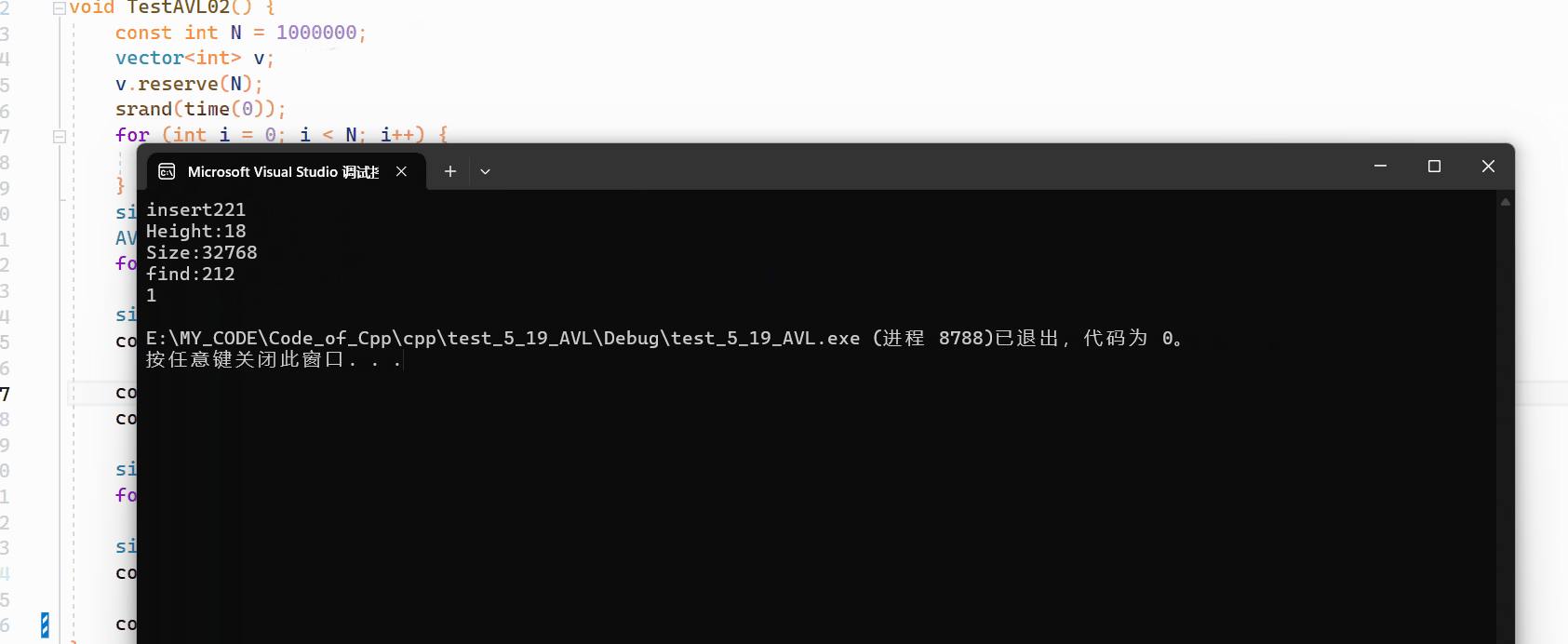
接着进行暴力测试,生成一百万个数据,主要测试性能和插入是否成功:
如上所示,插入一百万个数据也可以生成平衡树。
测试源码如下:
void TestAVL01() {int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };// {16, 3, 7, 11, 9, 26, 18, 14, 15}AVLTree<int, int> avtree;for (auto e : a) {if (e == 4) {int i = 0;}avtree.insert(make_pair(e, e));}avtree.InOrder();cout << avtree.height() << endl;cout << avtree.size() << endl;cout << avtree.IsBalance() << endl; }void TestAVL02() {const int N = 1000000;vector<int> v;v.reserve(N);srand(time(0));for (int i = 0; i < N; i++) {v.push_back(rand() + 1);}size_t begin1 = clock();AVLTree<int,int> tree;for (auto e : v)tree.insert({e, e});size_t end1 = clock();cout << "insert" << end1 - begin1 << endl;cout << "Height:" << tree.height() << endl;cout << "Size:" << tree.size() << endl;size_t begin2 = clock();for (auto e : v)tree.find(e);size_t end2 = clock();cout << "find:" << end2 - begin2 << endl;cout << tree.IsBalance() << endl; }
相关文章:
AVL树 ---(C++)
本篇讲全面的讲解 AVL 树的插入,旋转以及验证 AVL 树的性能(本篇未实现删除代码)。至于为什么会有 AVL 树,这是因为简单的二叉搜索树并不能直接的保证搜索的效率,因为当我们在二叉搜索树中插入一段有序的序列的时候&am…...
基于spring boot+MySQL 小区物业管理系统-计算机毕设 附源码37236
spring boot 小区物业管理系统 摘 要 在网络信息的时代,众多的软件被开发出来,给用户带来了很大的选择余地,而且人们越来越追求更个性的需求。在这种时代背景下,小区物业只能以客户为导向,以产品的持续创新作为小区物…...

Linux/Ubuntu/Debian常用服务管理命令
Linux/Ubuntu/Debian常用服务管理命令 在 Linux 系统中,服务管理是系统管理员日常维护工作的重要组成部分。通过一些常用的命令,我们可以查看服务状态、启动或停止服务、重启服务等。掌握这些命令,可以让系统管理工作更加高效和便捷。 1. s…...

Maven的三种项目打包方式——pom,jar,war的区别
1、pom:用在父级工程或聚合工程中,用来做jar包的版本控制,必须指明这个聚合工程的打包方式为pom。 聚合工程只是用来帮助其他模块构建的工具,本身并没有实质的内容。具体每个工程代码的编写还是在生成的工程中去写。 对于在父工程…...

[手游] 三色绘恋S Mobile Link
语音合成TTS: 文字转成语音的工具 WPS免登录一键修改器: 去除烦人的登录且能正常使用 故事简介: 深秋的雨季即将到来,正值那个为人所熟知的故事发生的前一年—— 地点:湖北省的重点高中,武汉师贰高校。 新学年开始,各…...

nss刷题(4)
1、[SWPUCTF 2021 新生赛]easyrce <?php error_reporting(0); highlight_file(__FILE__); if(isset($_GET[url])) { eval($_GET[url]); } ?> if(isset($_GET[url])) isset函数用来检测url变量是否存在;$_GET函数获取变量数据 eval($_GET[url]); eval函数用…...

iOS调整collectionViewCell顺序
效果图 原理 就是设置collectionView调整顺序的代理方法,这里要注意一点 调整过代理方法之后,一定要修改数据源,否则导致错乱。 还有就是在collectionView上面添加一个长按手势,在长按手势的不同阶段,调用collectionV…...

【回调函数】
1.回调函数是什么? 回调函数就是⼀个通过函数指针调用的函数。 如果你把函数的指针(地址)作为参数传递给另⼀个函数,当这个指针被用来调用其所指向的函数 时,被调用的函数就是回调函数。回调函数不是由该函数的实现方…...

找树左下角的值-力扣
本题个人认为不能叫做 找树左下角的值,左下角再怎么说也应当在树的左子树上,本题要求的节点是树最底层最左边的值。 首先想到的解法是对二叉树进行层序遍历,并记录本层第一个节点的值,当层序遍历结束时,此时记录的值即…...

【AI应用探讨】— Gemma2模型应用场景
目录 1. 金融风险管理 2. 营销策略优化 3. 医疗保健领域 4. 供应链管理 5. 人力资源管理 6. 自然语言处理(NLP) 7. 图像识别 8. 音频信号处理 9. 总结 1. 金融风险管理 场景描述:Gemma 2模型在金融领域可用于预测金融市场的波动性和…...
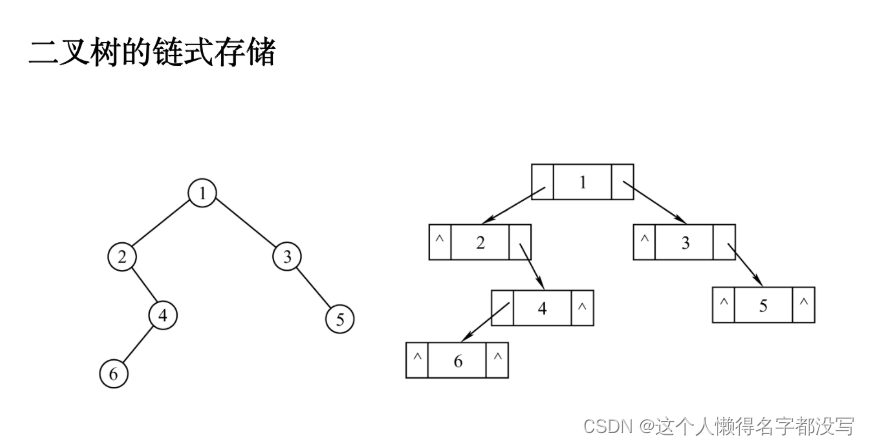
树二叉树
树 树是 n(n≥0)个结点的有限集。当 n 0时,称为空树。在任意一颗非空树中应满足: (1)有且仅有一个特定的称为根的结点。 (2)当 n > 1时,其余结点可分为 m&…...
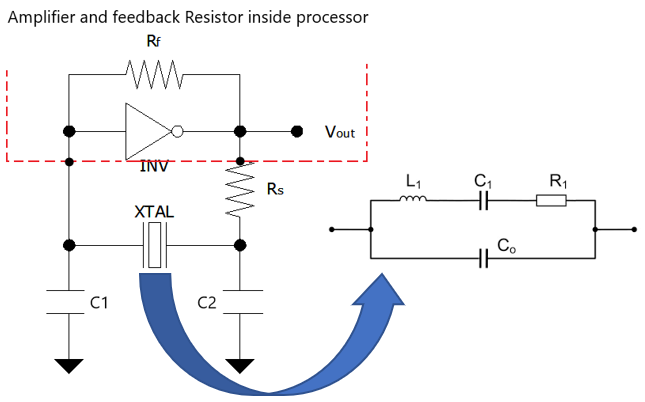
无源晶振振荡电路失效问题分析与解决策略
无源晶振(晶体谐振器)在电子设备中扮演着至关重要的角色,为数字电路提供稳定的时钟信号。然而,振荡电路一旦失效,可能会导致整个系统运行不正常。晶发电子将从三个主要方面分析无源晶振振荡电路失效的问题,…...

LIMS系统在汽车第三方检测实验室的应用
随着汽车行业的快速发展,汽车第三方检测实验室的工作量不断增加,对实验室的管理效率和数据准确性提出了更高的要求。LIMS系统的引入可以实现实验室的全面数字化管理,提高工作效率,降低运营成本,并提升数据质量与决策支…...

positivessl泛域名https证书
PositiveSSL,作为Sectigo旗下的子品牌,一直以来颁发的https数字证书产品性价比较高,适合大多数个人网站和中小型企业。其中,DV基础型的泛域名https证书以申请简单、颁发速度快、价格低受到众多用户的欢迎。今天就随SSl盾小编了解P…...

MySQL bin-log日志恢复数据
目录 一、开启二进制日志 二、检查二进制日志是否开启 三、使用二进制日志备份和恢复 使用二进制日志备份恢复前先创建备份: 应用二进制日志: 扩展用法: 四、常见命令和操作 五. 使用 mysqlbinlog 工具查看二进制日志 1. 查看二进制…...

Linux网络命令——netstat
netstat是Linux系统中非常有用的网络工具,被称为是网络监控中的军工刀,足见其地位。 传统上,它用于问题确定而不是性能测量,但是也可用于查看网络上的流量,以确定性能问题是否由于网络阻塞引起。 netstat用于显示与I…...

手机怎么压缩图片?通过三种压缩操作
手机怎么压缩图片?在智能手机日益普及的今天,拍照分享已成为日常生活的一部分。然而,高质量的照片往往占用较大的存储空间,且在网络上传输时速度较慢。那么,如何在手机上压缩图片呢?本文将介绍三种实用的手…...

分布式CAP、BASE理论务必了解一下
分布式系统理论是计算机科学中的一个重要分支,它关注如何设计和实现能够跨多个物理或逻辑位置运行的系统。在分布式系统中,CAP定理和BASE理论是两个非常著名的理论,它们分别描述了分布式系统设计中的一些基本约束和原则。 CAP定理 CAP定理&…...

spring最常用的注解
核心注解 Component 描述:将类标记为 Spring 组件,以便自动检测。用途:通常用于标注服务类或其他支持类。 Controller 描述:将类标记为 Spring MVC 控制器。用途:用于处理 Web 请求。 Service 描述:将类标记…...
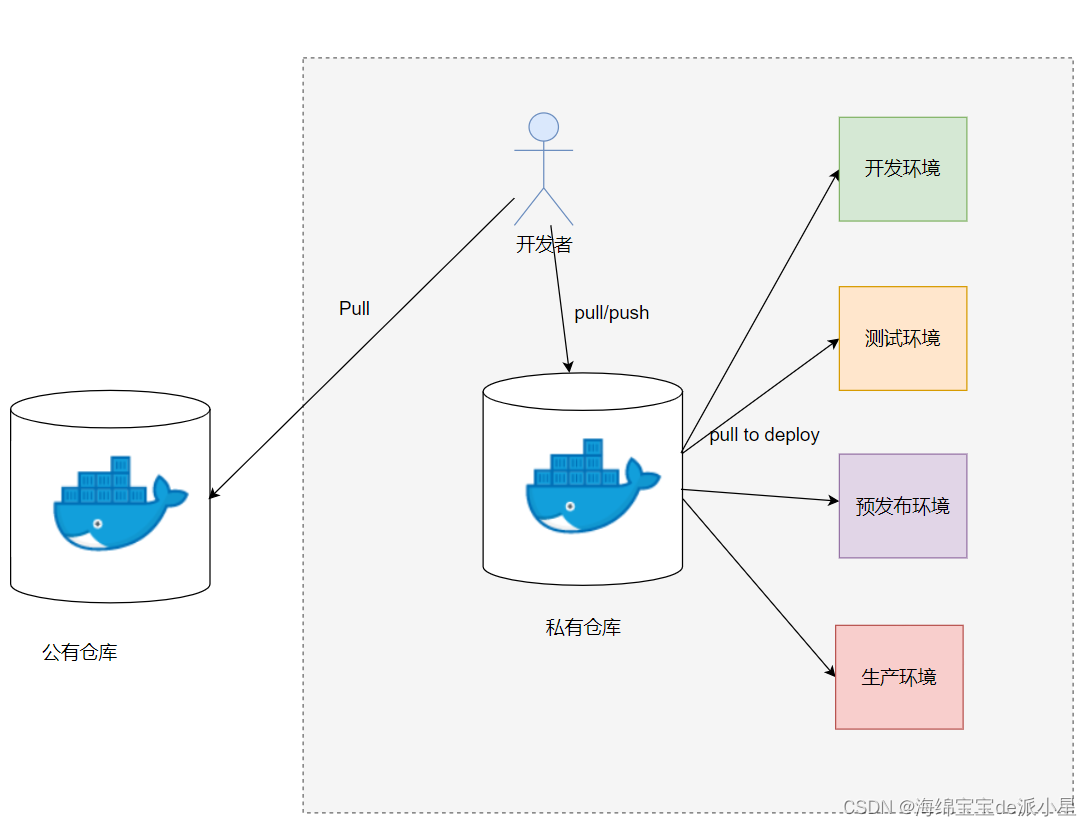
Docker:认识镜像仓库及其命令
文章目录 Docker Registry什么是Docker Registry 镜像仓库工作机制使用流程实际使用方法仓库的拉取机制 常用的镜像仓库---DockerHub什么是DockerHub私有仓库 镜像仓库命令docker logindocker pulldocker pushdocker searchdocker logout Docker Registry 什么是Docker Regist…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
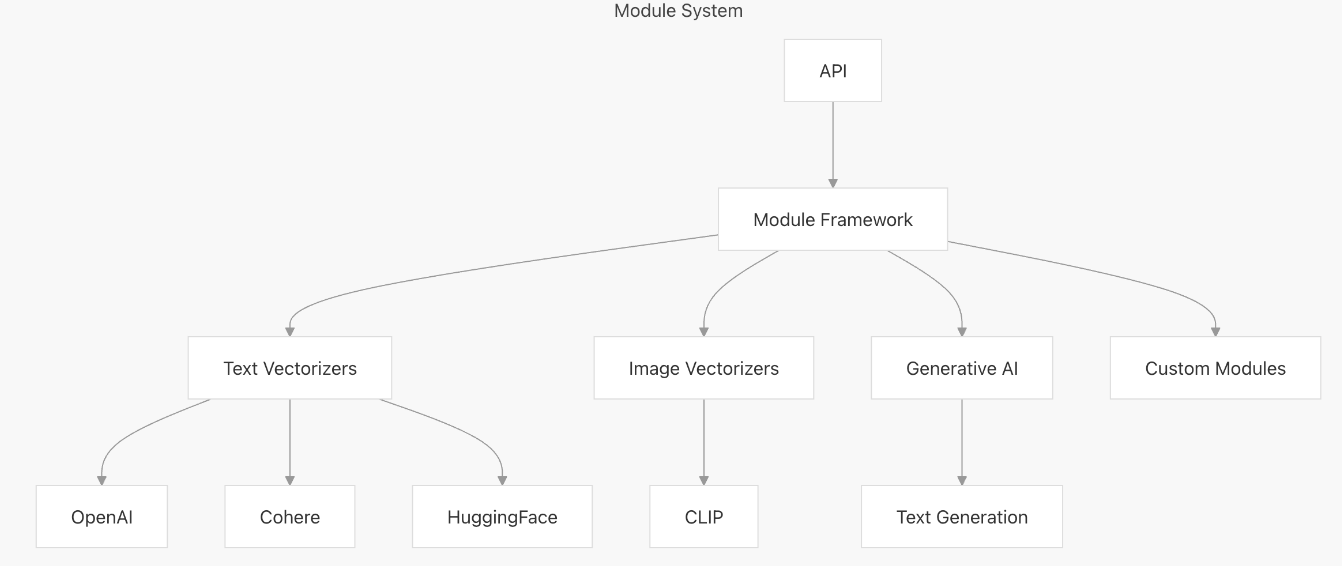
【向量库】Weaviate概述与架构解析
文章目录 一、什么是weaviate二、High-Level Architecture1. Core Components2. Storage Layer3. 组件交互流程 三、核心组件1. API Layer2. Schema Management3. Vector Indexing3.1. 查询原理3.2. 左侧:Search Process(搜索流程)3.3. 右侧&…...