【回调函数】
1.回调函数是什么?
回调函数就是⼀个通过函数指针调用的函数。
如果你把函数的指针(地址)作为参数传递给另⼀个函数,当这个指针被用来调用其所指向的函数
时,被调用的函数就是回调函数。回调函数不是由该函数的实现方直接调用,而是在特定的事件或条件发⽣时由另外的⼀方调用的,用于对该事件或条件进⾏响应。
只有调⽤函数的逻辑是有差异的,我们可以把调⽤的函数的地址以参数的形式传递过去,使⽤函数指针接收,函数指针指向什么函数就调⽤什么函数,这⾥其实使⽤的就是回调函数的功能。
接下来是一个简易计算器(利用回调函数)
#include <stdio.h>
int add(int a, int b)
{return a + b;
}
int sub(int a, int b)
{return a - b;
}
int mul(int a, int b)
{return a * b;
}
int div(int a, int b)
{return a / b;
}void calc(int(*pf)(int, int))
{int x, y;int ret = 0;printf("输入操作数:");scanf("%d %d", &x, &y);ret = pf(x, y);printf("ret = %d\n", ret);
}int main()
{int input = 1;do{printf("*************************\n");printf(" 1:add 2:sub \n");printf(" 3:mul 4:div \n");printf("********0. exit *********\n");printf("请选择:");scanf("%d", &input);switch (input){case 1:calc(add);break;case 2:calc(sub);break;case 3:calc(mul);break;case 4:calc(div);break;case 0:printf("退出程序\n");break;default:printf("选择错误\n");break;}} while (input);return 0;
}
图

下面是改造后的方法(利用数组函数进行优化,方便,减少冗余)
//加法
int add(int a, int b)
{return a + b;
}
//减法
int sub(int a, int b)
{return a - b;
}
//乘法
int mul(int a, int b)
{return a * b;
}
//除法
int div(int a, int b)
{return a / b;
}
//菜单
void menu()
{printf("*****************************\n");printf("********1.add 2.sub********\n");printf("********3.mul 4.div********\n");printf("******** 0.exit **********\n");printf("*****************************\n");
}
int main()
{int* (*pfArr[])(int, int) = {NULL,add ,sub,mul,div};//函数指针数组,存放函数int input = 0;int x = 0;int y = 0;int ret = 0;do {menu();printf("请选择");scanf("%d", &input);if (input >= 1 && input <= 4) {printf("请输入两个操作数:");scanf("%d %d", &x, &y);ret = pfArr[input](x, y);//这里进行调用函数数组里面的函数printf("%d\n",ret);}else if(input==0){printf("退出\n");}else {printf("选择错误,重新选择");}} while (input);return 0;
}相关文章:

【回调函数】
1.回调函数是什么? 回调函数就是⼀个通过函数指针调用的函数。 如果你把函数的指针(地址)作为参数传递给另⼀个函数,当这个指针被用来调用其所指向的函数 时,被调用的函数就是回调函数。回调函数不是由该函数的实现方…...

找树左下角的值-力扣
本题个人认为不能叫做 找树左下角的值,左下角再怎么说也应当在树的左子树上,本题要求的节点是树最底层最左边的值。 首先想到的解法是对二叉树进行层序遍历,并记录本层第一个节点的值,当层序遍历结束时,此时记录的值即…...

【AI应用探讨】— Gemma2模型应用场景
目录 1. 金融风险管理 2. 营销策略优化 3. 医疗保健领域 4. 供应链管理 5. 人力资源管理 6. 自然语言处理(NLP) 7. 图像识别 8. 音频信号处理 9. 总结 1. 金融风险管理 场景描述:Gemma 2模型在金融领域可用于预测金融市场的波动性和…...
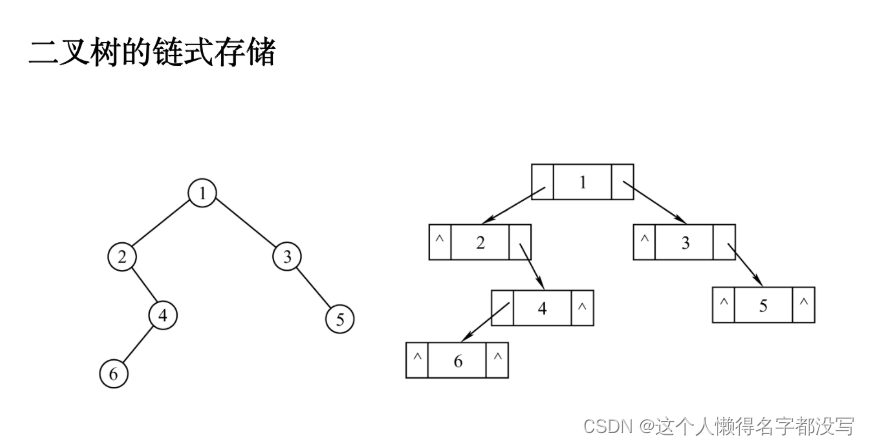
树二叉树
树 树是 n(n≥0)个结点的有限集。当 n 0时,称为空树。在任意一颗非空树中应满足: (1)有且仅有一个特定的称为根的结点。 (2)当 n > 1时,其余结点可分为 m&…...
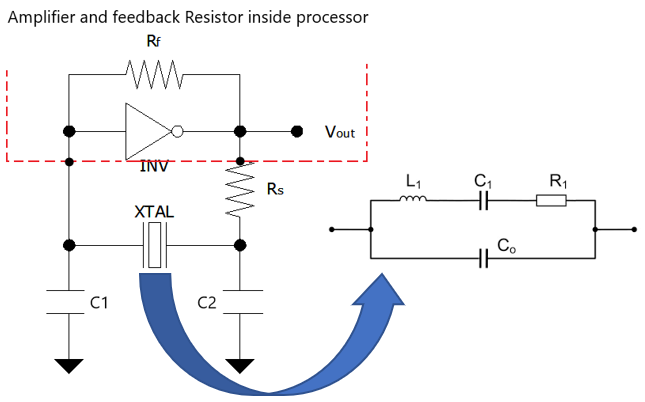
无源晶振振荡电路失效问题分析与解决策略
无源晶振(晶体谐振器)在电子设备中扮演着至关重要的角色,为数字电路提供稳定的时钟信号。然而,振荡电路一旦失效,可能会导致整个系统运行不正常。晶发电子将从三个主要方面分析无源晶振振荡电路失效的问题,…...

LIMS系统在汽车第三方检测实验室的应用
随着汽车行业的快速发展,汽车第三方检测实验室的工作量不断增加,对实验室的管理效率和数据准确性提出了更高的要求。LIMS系统的引入可以实现实验室的全面数字化管理,提高工作效率,降低运营成本,并提升数据质量与决策支…...

positivessl泛域名https证书
PositiveSSL,作为Sectigo旗下的子品牌,一直以来颁发的https数字证书产品性价比较高,适合大多数个人网站和中小型企业。其中,DV基础型的泛域名https证书以申请简单、颁发速度快、价格低受到众多用户的欢迎。今天就随SSl盾小编了解P…...

MySQL bin-log日志恢复数据
目录 一、开启二进制日志 二、检查二进制日志是否开启 三、使用二进制日志备份和恢复 使用二进制日志备份恢复前先创建备份: 应用二进制日志: 扩展用法: 四、常见命令和操作 五. 使用 mysqlbinlog 工具查看二进制日志 1. 查看二进制…...

Linux网络命令——netstat
netstat是Linux系统中非常有用的网络工具,被称为是网络监控中的军工刀,足见其地位。 传统上,它用于问题确定而不是性能测量,但是也可用于查看网络上的流量,以确定性能问题是否由于网络阻塞引起。 netstat用于显示与I…...

手机怎么压缩图片?通过三种压缩操作
手机怎么压缩图片?在智能手机日益普及的今天,拍照分享已成为日常生活的一部分。然而,高质量的照片往往占用较大的存储空间,且在网络上传输时速度较慢。那么,如何在手机上压缩图片呢?本文将介绍三种实用的手…...

分布式CAP、BASE理论务必了解一下
分布式系统理论是计算机科学中的一个重要分支,它关注如何设计和实现能够跨多个物理或逻辑位置运行的系统。在分布式系统中,CAP定理和BASE理论是两个非常著名的理论,它们分别描述了分布式系统设计中的一些基本约束和原则。 CAP定理 CAP定理&…...

spring最常用的注解
核心注解 Component 描述:将类标记为 Spring 组件,以便自动检测。用途:通常用于标注服务类或其他支持类。 Controller 描述:将类标记为 Spring MVC 控制器。用途:用于处理 Web 请求。 Service 描述:将类标记…...
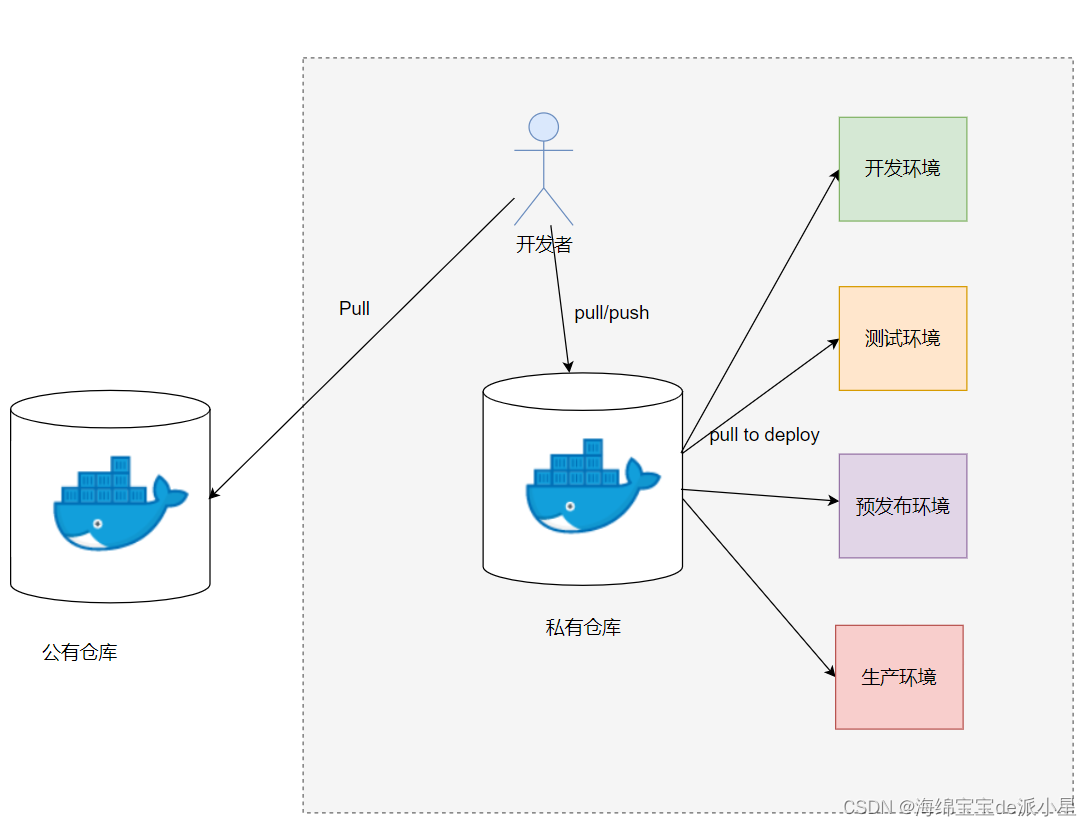
Docker:认识镜像仓库及其命令
文章目录 Docker Registry什么是Docker Registry 镜像仓库工作机制使用流程实际使用方法仓库的拉取机制 常用的镜像仓库---DockerHub什么是DockerHub私有仓库 镜像仓库命令docker logindocker pulldocker pushdocker searchdocker logout Docker Registry 什么是Docker Regist…...

使用 Django 创建 App
文章目录 步骤 1:创建 Django 项目步骤 2:创建 App步骤 3:配置 App步骤 4:编写代码步骤 5:运行服务器 在 Django 中,App 是组织代码的基本单元,它可以包含模型、视图、模板等组件,帮…...

java定时任务 设置开始时间、结束时间;每周一、四、六执行;并且隔n周执行。最后计算所有执行时间
java定时任务 设置开始时间、结束时间;每周一、四、六执行;并且隔n周执行。最后计算所有执行时间) 定时任务需求程序设计依赖引入程序一、计算开始时间那周的周一时间二、根据executeTime和weekList.get(n),计算每个cron表达式。三、根据一和…...

linux的持续性学习
安装php 第一步:配置yum源 第二步:下载php。 yum install php php-gd php-fpm php-mysql -y 第三步:启动php。 systemctl start php-fpm 第四步:检查php是否启动 lsof -i :9000 计划任务 作用&am…...

MyBatis:概念简章
1. hello world 配置文件:mybatis-config.xml(核心配置文件,用于配置连接的数据库信息)(一般一个)XxxMapper.xml 该文件用于操作表(执行sql语句)(一张表一个)…...

有什么接码平台比较好用的
接码平台,也被称作短信接收平台或虚拟号码服务,主要是提供可以接收短信验证码的虚拟手机号码服务。这种服务通常被用于需要在网络平台上注册大量账号的情况,如营销推广、应用测试或是海淘购物时所需的手机号验证。下面将推荐几个较为好用的接…...
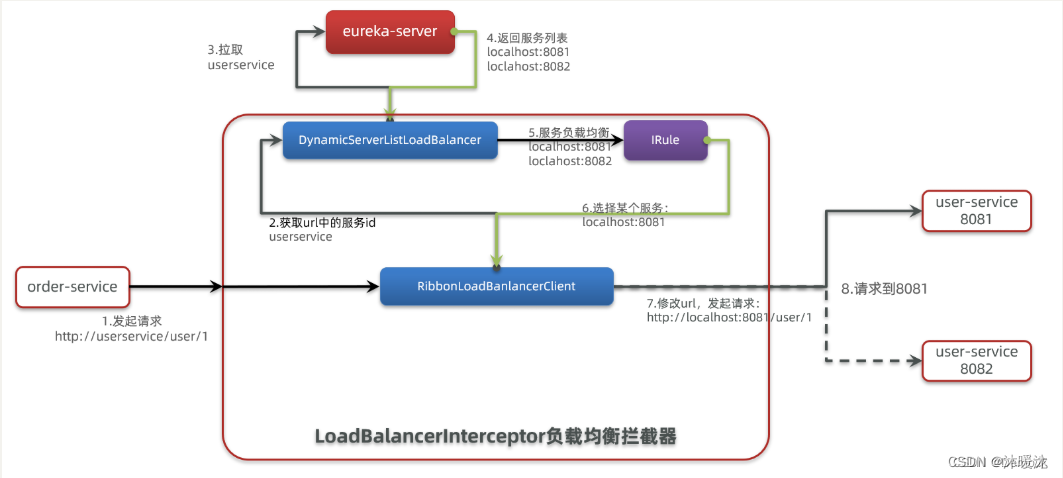
微服务之负载均衡器
1、负载均衡介绍 负载均衡就是将负载(工作任务,访问请求)进行分摊到多个操作单元(服务器,组件)上 进行执行。 根据负载均衡发生位置的不同, 一般分为服务端负载均衡和客户端负载均衡。 服务端负载均衡指的是发生在服务提供者一方ÿ…...

《时间管理九段》前四阶段学习笔记
文章目录 0.何谓时间管理九段0.1 第一段--把一件事做好0.2 第二段--把一天过好0.3 第三段--掌控两周内的固定日程0.4 第四段--掌控两周内的弹性时间0.5 第五段--科学管理3个月的项目事件0.6 第六段--实现一年的梦想0.7 第七段--明确一生的愿景0.8 第八段--正确补充和释放自身能…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
