【递归、搜索与回溯】穷举vs暴搜vs深搜vs回溯vs剪枝
穷举vs暴搜vs深搜vs回溯vs剪枝
- 1.全排列
- 2.子集

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励,我们一起努力吧!😃😃
管他什么深搜、回溯还是剪枝,画出决策树就完事了~~~
1.全排列
题目链接:46. 全排列
题目描述:

算法原理:
其实这道题本身是一个穷举(枚举)的题,3个数你可以三层for循环,但是如果10个数,100个数呢?对于数多的显然不合适!此时我们就需要借助递归把所有情况都枚举出来。
解决回溯的步骤:
- 画出决策树,越详细越好!
- 设计代码
全局变量
dfs函数
细节问题
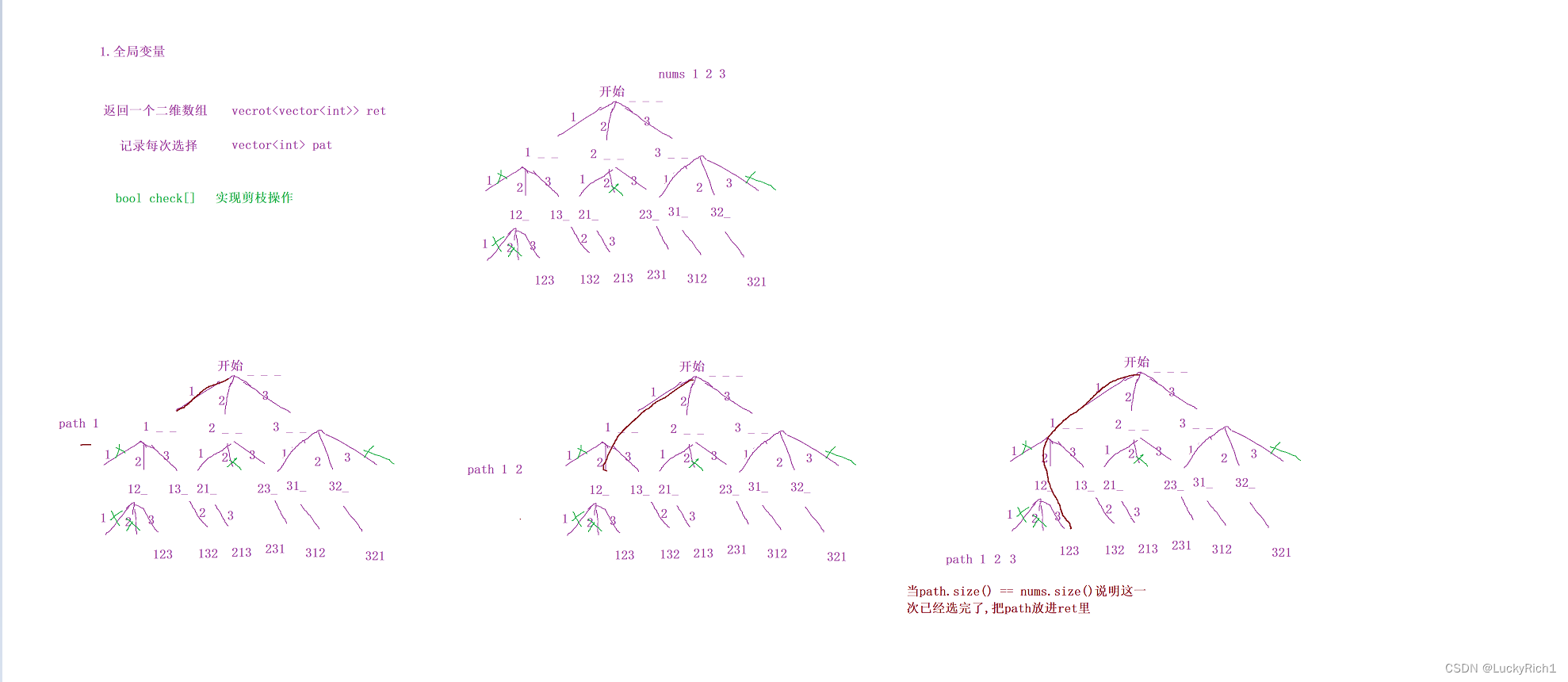
1.画出决策树
就是在暴力枚举这道题过程中如何不重不漏的把所有情况枚举到,就是把自己的想想法按照树的样子画下来。
第一次选择可以直接选123中任何一个,接下来每次选择都是从123中选。但是此时你会发现比如第一次选1,下一次还选1就会有重复的情况,因此这个1我们是要把它剪掉的,不考虑有1的情况。第二次选择假设选择的是2,在往下选择就还是有123,但是此时剪掉的应该更多,12不能选,只能选3,所有最终这条分支就是123,同理其他也是这样选出。

决策树画的越详细越好,就是把每一步都画出来,这样你就会发现每一个节点干的事情都是一样的,都是枚举整个数组。无非就是一些分支被我们剪掉。当一直在干同一件事情的时候我们决策树就画成功了,因为可以改成递归的代码。
2.设计代码
1.全局变量
全局变量就看这个递归需要什么东西和以及最终要返回什么东西。
全局变量的使用仁者见仁智者见智,也可以把全局变量换成参数在递归函数中传递。看个人选择,不过还是建议使用全局变量!
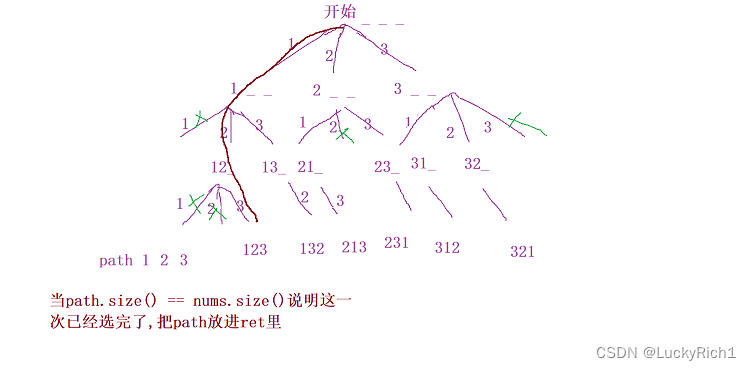
首先来递归要返回的二维数组,再来一个把每次选择都要记录的path。
当path.size() == nums.size() 说明已经找到一个符合的组合,此时把path放到ret里,然后回溯 ,注意要 恢复现场。在说这个之前我们要说一说这个剪枝的事情。

剪枝怎么解决?就是如果避免下一次选择重复的数字。
此时我们也需要一个数组,弄一个bool 类型的数组。来判断一下该条路径下的数是否已经被使用过了。bool数组中记录nums数组中的数字是否已经被使用过。
check[0] 对应 1, check[1] 对应 2 , check[2] 对应3,check初始化都为false,只有对应数字被使用了 check[i]=true,说明这个数字已经被使用过了,下一次就不要选这个数字了。
2.dfs函数
仅需关心,某一个节点在干什么事情。
3.细节问题
回溯
当我要回去的时候,需要把这个3干掉,就是向上回去把path最后一个元素干掉,但是别忘记了check也是一个全局的, 你用3的时候会把check对应位置置为true,那你向上返回这个3你都不用了,是不是要把3复原啊。
- 干掉 path 最后一个元素
- 修改 check 数组
剪枝
这里前面说过。
递归出口
遇到叶子节点的时候,直接添加结果。不用在到空了。
这样的题一定是决策树画出来是最重要的,第二步设计代码你想到哪一点写那一点都可以。
class Solution {vector<vector<int>> ret;vector<int> path;bool check[7]={false};
public:vector<vector<int>> permute(vector<int>& nums) {dfs(nums);return ret;}void dfs(vector<int>& nums){if(path.size() == nums.size()){ret.push_back(path);//返回之前可以 回溯 --> 恢复现场return;}for(int i=0;i<nums.size();++i){//剪枝if(check[i] == false){path.push_back(nums[i]);check[i]=true;dfs(nums);//返回之后也可以 回溯 ---> 恢复现场 ,建立返回之后check[i]=false;path.pop_back(); }}}
};
注意一定是决策树越详细后面代码设计越轻松,代码设计考虑一下全局变量、dfs函数、细节问题。
2.子集
题目链接:78. 子集
题目描述:

算法原理:
这里我们采用两种策略来解决这个问题,虽然是两种策略,但都是深搜,所以我们的思考方式是一样的。
解法一:
- 画出决策树
- 设计代码
全局变量
dfs
细节:回溯、剪枝、递归出口
首先画决策树,我们想想如何能够把所有子集不重不漏全部枚举出来。我们从子集定义出发,子集是这个数组里面选or不选某些数形成新的集合就是它的子集。因此我们就单独盯着数组中每个数字考虑选or不选来画出我们的决策树。
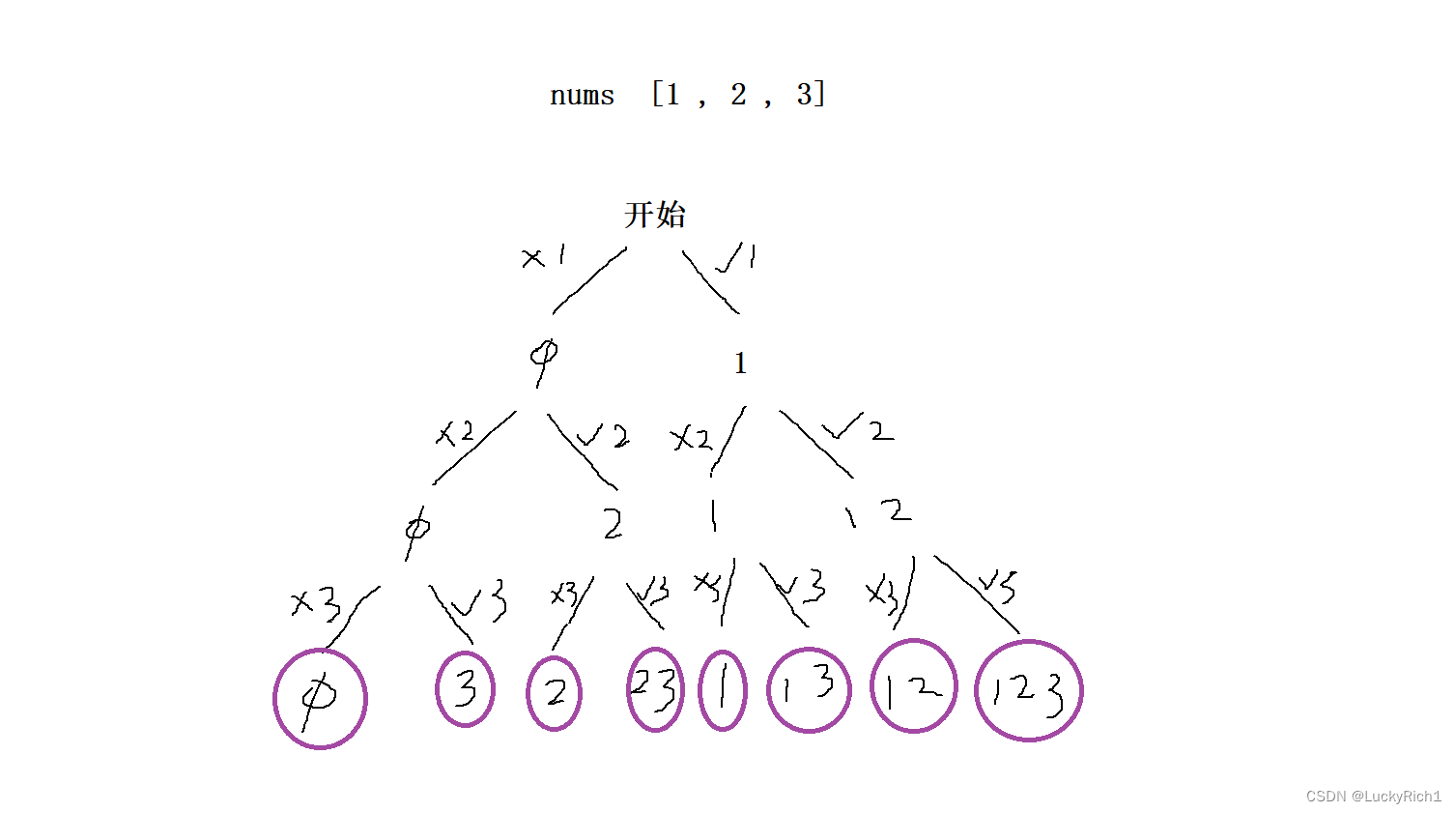
此时所有叶子节点就是数组所有不重复的子集。
现在我们仅需把这颗决策树转换成代码就可以了。之前的题无非就是直接把树画好给我们了,现在是要我们自己画一颗树。
既然叶子节点是我们的结果,因此我们需要两个全局变量,一个二维数组ret,一个一维数组path,path把每次选or不选路径记录下来,然后ret把path记录下来。这道题我们并不需要剪枝。
dfs函数我们就盯着某一个位置在干什么。比如绿圈的位置,因为上面已经选过了,所以要需要考虑这一次的数选or不选,所以dfs不仅要这个nums,还要告诉我你当前选到了那个位置,dfs(nums,pos)
选就加入到path里,然后dfs(nums,pos+1)下一层
不选直接 dfs(nums,pos+1)下一层
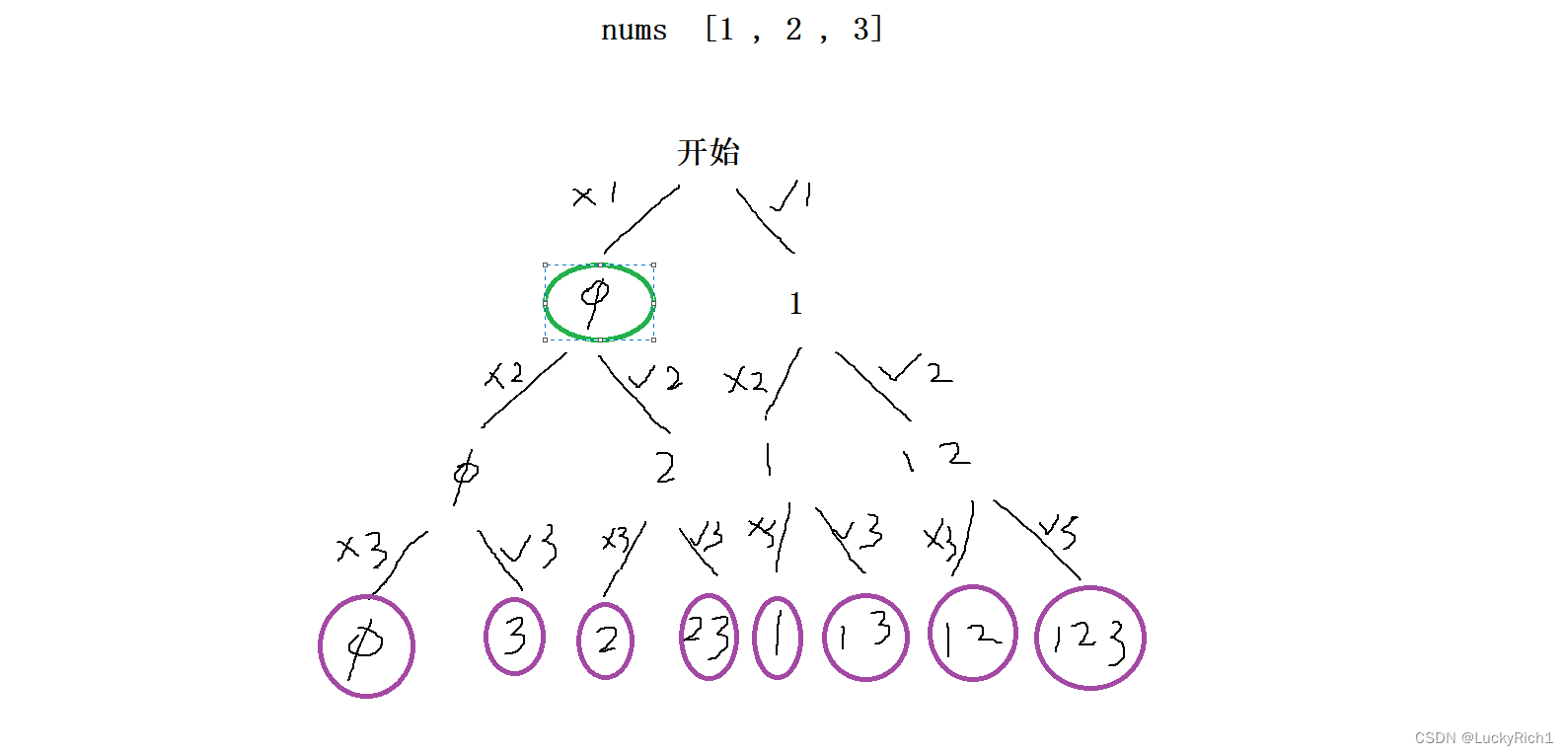
细节问题:回溯要恢复现场,因此我们在选的这条路径在递归返回之后把path最后一个位置pop掉,剪枝我们这里没有。递归出口当pos==nums.size()的时候,把path放到ret里,然后返回即可。
class Solution {vector<vector<int>> ret;vector<int> path;
public:vector<vector<int>> subsets(vector<int>& nums) {dfs(nums,0);return ret;}void dfs(vector<int>& nums,int pos){if(pos == nums.size()){ret.push_back(path);return;}// 选path.push_back(nums[pos]);dfs(nums,pos+1);path.pop_back(); // 恢复现场// 不选dfs(nums,pos+1);}
};
解法二:
也是上面一样的步骤,
- 画出决策树
- 设计代码
全局变量
dfs
细节:回溯、剪枝、递归出口
这里我们换一种思考方式,当我们选的子集是没有元素、只有一个元素、只有两个元素、只有三个元素等等。前面的是盯着某一个数选or不选,现在我们直接看看最终要的子集要么没有,要么一个元素,要么两个元素,要么三个元素等等,从小到大去选。并且每次是从这个被选的数的后面再次选。并且每一个节点都是我们想要的结果。

你会发现我们这种解法比上面少了很多没有必要的情况。
全局变量还是上面那两个,dfs函数 从当前节点位置开始向后枚举,所以也要知道当前位置 dfs(nums,pos)。for(int i=pos;i<nums.size();++i) 把路径上的节点放入path,然后递归到下一层dfs(nums,pos+1),当递归返回收把path最后一个位置pop掉。 回溯也要恢复现场,把path最后一个位置pop掉,这里我们不用剪枝,递归出口,每次进入递归函数后先把path先放到ret里。然后也不需要出口,循环条件不满足就出去了。
class Solution {vector<vector<int>> ret;vector<int> path;
public:vector<vector<int>> subsets(vector<int>& nums) {dfs(nums,0);return ret;}void dfs(vector<int>& nums,int pos){ret.push_back(path);for(int i=pos;i<nums.size();++i){path.push_back(nums[i]);dfs(nums,i+1);path.pop_back(); // 恢复现场}}
};
相关文章:

【递归、搜索与回溯】穷举vs暴搜vs深搜vs回溯vs剪枝
穷举vs暴搜vs深搜vs回溯vs剪枝 1.全排列2.子集 点赞👍👍收藏🌟🌟关注💖💖 你的支持是对我最大的鼓励,我们一起努力吧!😃😃 管他什么深搜、回溯还是剪枝,画出决…...
)
celery-redbeat方案(动态定时任务、异步任务)
文章目录 为什么选择 RedBeat?方案坑事项记录 记一次工作上的问题 问题:项目上当前定时任务框架和服务端耦合,容易出现加载定时任务时间很长,影响后端服务启动,容易改动引发定时任务的问题。且能方便的动态的增加或删除…...

js解析成语法树以及还原
const {parse} require("babel/parser"); const traverse require("babel/traverse").default; const generator require("babel/generator").default;// 1.定义要处理的代码 const jscode function square(n) {return n * n; };// 2.使用ba…...

基于python可伸缩JSON格式列表实现
对于消息体为一个json格式列表,列表长度变化的代码设计,如下实现可供参考。 1、python语言实现(直接取值) #codingutf-8n 2 # 行项目数 productCode [11111,222222,333333] unit [H06,H07,H08] qty [6,7,8] items []for i in range(0, n):item …...

h5相机功能
h5相机功能 利用vant input file <template><div class"mb10"><divv-for"(item, index) in info.imgList":key"index"class"imgItem f32 mr20"click"preview(item, index)"><img :src"doFileUrl…...
IDEA | 安装通义灵码插件,开启智能编码旅程
安装步骤 从插件市场安装,点击导航-插件,打开应用市场,搜索通义灵码(TONGYI Lingma),找到通义灵码后点击安装。 https://tongyi.aliyun.com/lingma/download 使用方式 https://help.aliyun.com/documen…...
过程中遇到的挑战?)
技术人员如何克服在使用行列视(RCV)过程中遇到的挑战?
技术人员在使用行列视(RCV)过程中可能会遇到多种挑战,以下是一些建议,帮助他们克服这些挑战: 1. 深入了解系统架构和功能: - 熟练掌握RCV的架构设计,包括数据中心层、计算服务层、函数层、人机…...

手把手教你安装 Vivado2019.2(附安装包)
一、Vivado 2019.2优点 Vivado 2019.2 作为 Xilinx 公司发布的一款设计套件版本,具有多个显著的优点,以下是对其优点的详细归纳: 集成度高:开发工具丰富并行综合功能灵活的许可证策略用户友好的界面强大的仿真和验证功能丰富的文…...
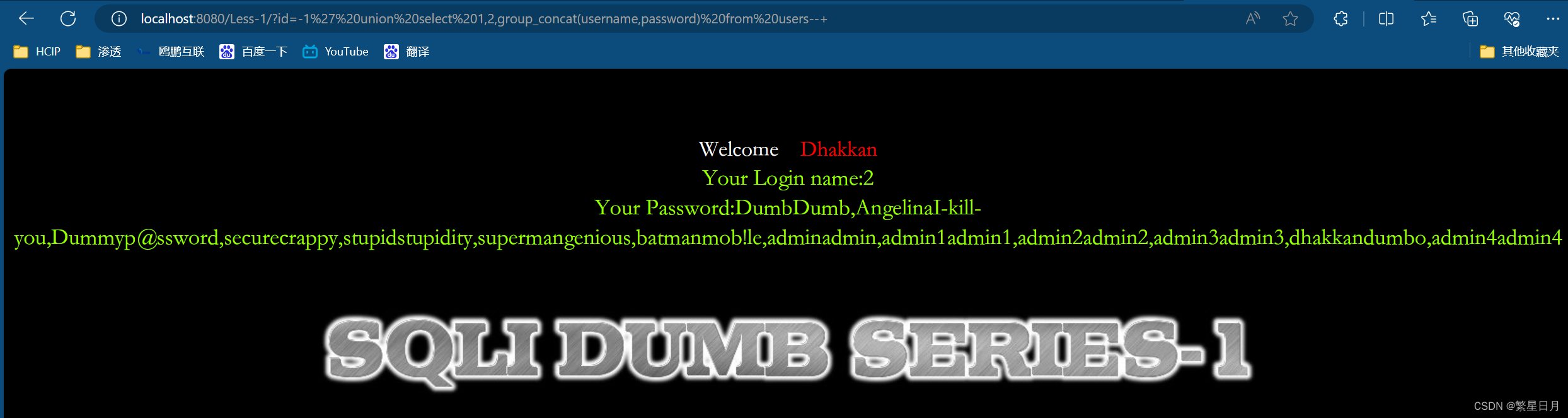
Sql-labs的第一关
前言 我们在使用Sql-libs靶场进行Sql注入实验的时候,前提要求我们对mysql数据库结构要有一个大概的了解,因为mysql5.0以上的版本都会自带一个名为information_schema的数据库,这个数据库下面会有columns和tables两个表。 tables这个表的table…...

10_1 Linunx Web服务管理
10_1 Linunx Web服务管理 文章目录 10_1 Linunx Web服务管理[toc]1. 环境准备2. Web服务2.1 Web服务简介 2.2 Web配置2.2.1 提供的默认配置2.2.2 Web服务的主配置文件2.2.3 /etc/httpd/conf/httpd.conf 文件反映出来的”访问控制信息“2.2.4 修改监听端口,访问2.2.5…...

苹果WWDC 2024:十三大亮点公布,一切都有关AI|TodayAI
在刚刚结束的苹果全球开发者大会(WWDC 2024)上,苹果公司展示了一系列令人瞩目的新功能,特别是在人工智能(AI)领域的重大进展。以下是本次大会的十三大亮点。 1. 苹果推出首个AI系统 苹果宣布推出其首个AI系统——Apple Intelligence,这一系统将强大的生成模型直接集成到…...

Nginx访问日志
Nginx日志是Nginx Web服务器产生的记录文件,主要用于跟踪和分析服务器的访问情况以及错误信息。Nginx日志主要分为两大类:访问日志 (access_log): 访问日志记录了每一次客户端对Nginx服务器的HTTP请求的详细信息,这对于统计分析、流量监控、用…...
Java使用Hutool工具类轻松生成验证码
一、效果展示 二、Hutool工具类实现验证码生成 2.1 引入依赖 <!--hutool工具包--> <dependency><groupId>cn.hutool</groupId><artifactId>hutool-all</artifactId><version>5.7.15</version> </dependency2.2 简单实现方…...

leetcode 40. 组合总和 II
题目 给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的每个数字在每个组合中只能使用 一次 。 注意:解集不能包含重复的组合。 原题链接:https://leetc…...
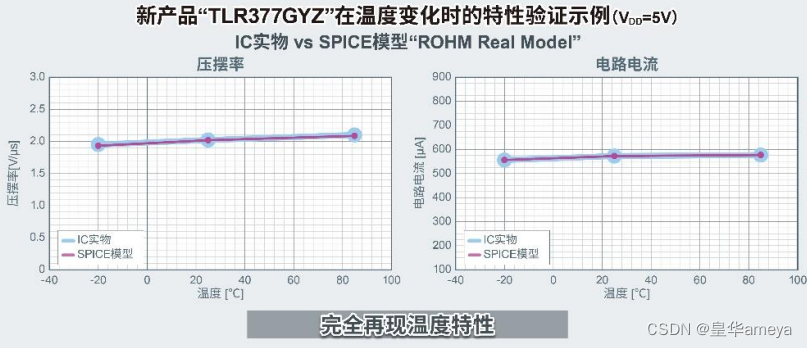
AMEYA360代理品牌:ROHM开发出世界超小CMOS运算放大器,适用于智能手机和小型物联网设备等应用
全球知名半导体制造商ROHM(总部位于日本京都市)开发出一款超小型封装的CMOS运算放大器“TLR377GYZ”,该产品非常适合在智能手机和小型物联网设备等应用中放大温度、压力、流量等的传感器检测信号。 智能手机和物联网终端越来越小型化,这就要求搭载的元器…...

第1章Hello world 4/5:对比Rust/Java/C++创建和运行Hello world全过程:运行第一个程序
讲动人的故事,写懂人的代码 1.7 对比Rust/Java/C++创建和运行Hello world全过程 有了会听懂人类的讲话,还能做记录的编程助理艾极思,他们三人的讨论内容,都可以变成一份详细的会议纪要啦。 接下来,我们一起看看艾极思是如何记录下赵可菲创建和运行Java程序Hello world,…...

golang优雅代码【lock实现】
golang优雅代码【lock实现】 1.局部锁1.1 具体实现方式 本文代码风格来源参考 database/sql 包 更加深刻理解go语言圣经中函数是一等公民 1.局部锁 database/sql源码中使用 withLock(dc, func(){...}) 方法实现局部锁,完美利用了 golang 的 defer 关键字对 入参dc…...
)
Dijkstra算法(迪杰斯特拉算法)
迪杰斯特拉算法通常用在图的最短路径问题上 而迷宫的最短路径可以用BFS来做,虽然BFS不能用于带权值的迷宫,但是可以对BFS稍微改进,只需要把判断是否走过的数组改为最短路径的数组,在判断是否可走时判断是否比最短的小即可 Dijks…...
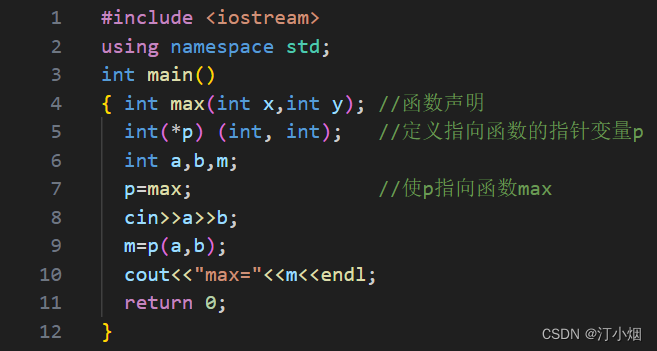
用函数指针求a和b中的大者
指针变量也可以指向一个函数。一个函数在编译时被分配给一个入口地址。这个函数入口地址就称为函数的指针。可以用一个指针变量指向函数,然后通过该指针变量调用此函数。 先按一般方法编写程序: 可以用一个指针变量指向max函数,然后通过该指…...

鸿蒙轻内核M核源码分析系列六 任务及任务调度(2)任务模块
任务是操作系统一个重要的概念,是竞争系统资源的最小运行单元。任务可以使用或等待CPU、使用内存空间等系统资源,并独立于其它任务运行。鸿蒙轻内核的任务模块可以给用户提供多个任务,实现任务间的切换,帮助用户管理业务程序流程。…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...
