C/C++ 进阶(6)红黑树
个人主页:仍有未知等待探索-CSDN博客
专题分栏:C++
目录
一、概念
性质
二、操作
插入
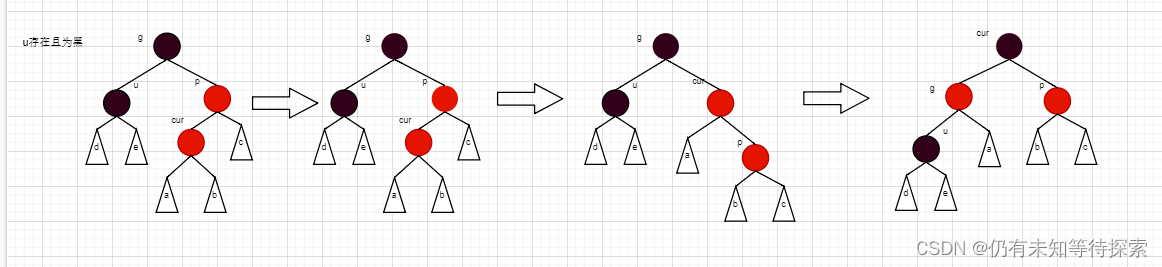
情况一:cur为红、p为红、g为黑,如果u存在且为红
步骤:
情况二:cur为红、p为红、g为黑,如果u不存在或者u存在且为黑
情况a步骤:
情况b步骤:
情况三:cur为红、p为红、g为黑,如果u不存在或者u存在且为黑
步骤:
三、总代码
一、概念
红黑树是一颗特殊的二叉搜索树。红黑树虽然不要求是平衡的,但是该树的最长路径不超过最短路径的二倍。
红黑树避免了过多的旋转问题。
性质
1、每个节点的颜色不是红色就是黑色。
2、根节点的颜色是黑色。
3、如果一个节点的颜色是红色,则该节点的左右孩子节点都是黑色。
4、对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点。
5、每个叶子节点(这里的叶子节点指的是null节点)的颜色都是黑色的。
二、操作
插入
插入一个新节点之后,会遇到几种情况,需要我们自己对红黑树进行调整,来保证其性质的正确。
新插入节点的颜色为红色。如果为黑色的话,性质4可能会不满足,相较于性质3来说,调整起来会比较麻烦。
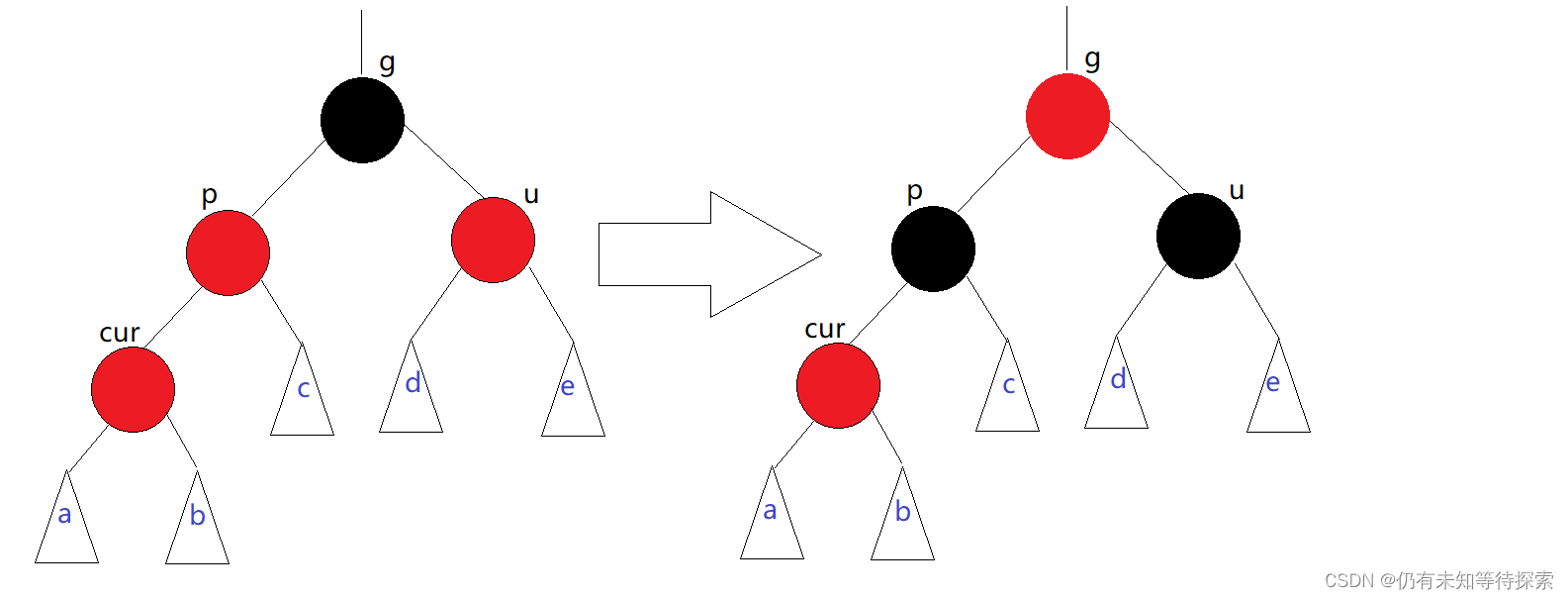
情况一:cur为红、p为红、g为黑,如果u存在且为红
步骤:
- 将 p、u 变成黑色,g 变成红色。
- 如果 g 为整个树的根节点,则将 g 变成黑色。
- 如果 g 不是根节点,且双亲结点为红色的话,继续向上进行变换。
- 如果 g 不是根节点,且双亲结点为黑色的话,则结束。
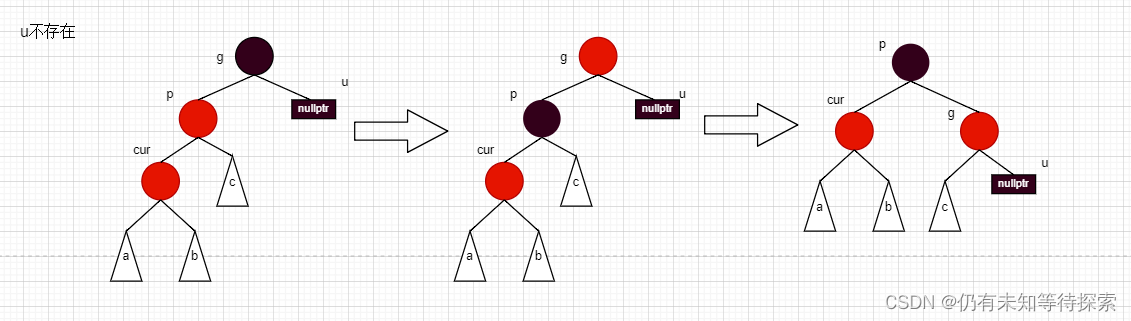
情况二:cur为红、p为红、g为黑,如果u不存在或者u存在且为黑
对于这个情况二,还有两种不同的情况。注:p 节点一定是 cur 节点的双亲结点。
情况a:cur 为 p 的左孩子,p 为 g 的左孩子。
情况b:cur 为 p 的右孩子、p 为 g 的右孩子。
情况a步骤:
- 将 p 变成黑色,g 变成红色。
- 以 g 为旋转点,进行右单旋。
情况b步骤:
- 将 p 变成黑色,g 变成红色。
- 然后以 g 为旋转点,进行左单旋。
另外一种情况,u 不存在,就需要自己去琢磨咯。
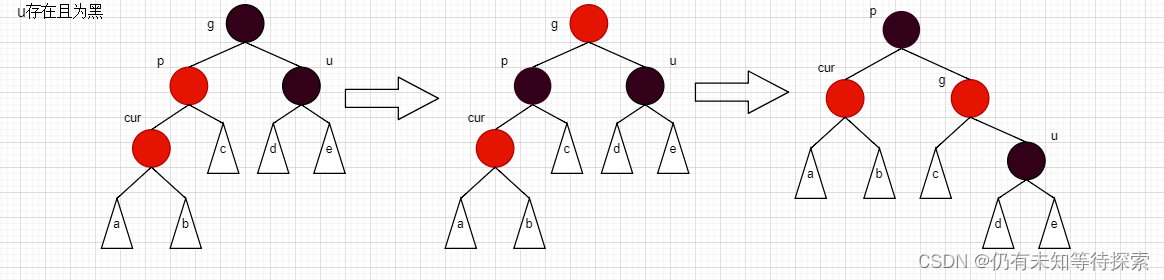
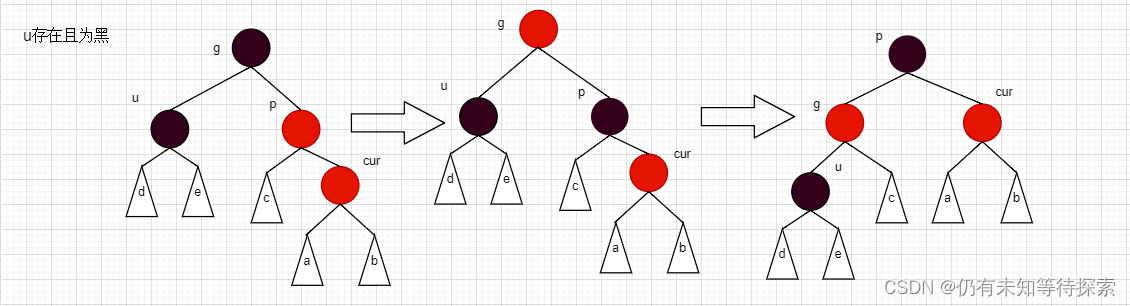
情况三:cur为红、p为红、g为黑,如果u不存在或者u存在且为黑
情况三是情况二的补充。对于情况二,我们只讲了上述的两种情况。剩余的情况则在这里进行解释。
情况a:cur 为 p 的左孩子,p 为 g 的右孩子。
情况b:cur 为 p 的右孩子、p 为 g 的左孩子。
对于上述情况,想必大概也能猜测出来,这种情况要对红黑树进行双旋处理了。这里仅对情况a 且 u 存在进行画图分析。
步骤:
- 先以 p 为旋转点进行右单旋,然后再以 g 为旋转点进行左单旋。
- 然后将 cur 变成黑色,g 变成红色。
三、总代码
#include <iostream>
#include <assert.h>
#include <vector>
using namespace std;enum color
{Red,Black
};
template <class K, class V>
struct RBTreeNode
{typedef pair<K, V> PKV;RBTreeNode(const PKV& e = PKV()):_left(nullptr),_right(nullptr),_parent(nullptr),_col(Red),_val(e){}struct RBTreeNode<K, V>* _left;struct RBTreeNode<K, V>* _right;struct RBTreeNode<K, V>* _parent;int _col;PKV _val;
};template<class K, class V>
class RBTree
{
public:typedef RBTreeNode<K, V> node;typedef pair<K, V> PKV;RBTree():_root(nullptr){}void insert(const PKV& e){// 根据二叉搜索树插入的方式进行插入node* cur = _root;node* parent = cur;while (cur){parent = cur;if (cur->_val.first > e.first){cur = cur->_left;}else{cur = cur->_right;}}cur = new node(e);if (parent == nullptr){_root = cur;}else{if (parent->_val.first > cur->_val.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;}// 更新,对于不同的情况,进行不同的调整// parent 为黑、不存在,结束node* p = parent;while (p && p->_col == Red){node* g = p->_parent;if (g->_left == p){node* u = g->_right;// 叔叔存在且为红if (u && u->_col == Red){p->_col = u->_col = Black;g->_col = Red;// 继续往上处理cur = g;p = cur->_parent;}// 叔叔不存在且为黑else {// g// p u// cif (cur == p->_left){// 右单旋RotateR(g);// 变色g->_col = Red;p->_col = Black;}// g// p u// celse {// 左右双旋RotateL(p);RotateR(g);// 变色cur->_col = Black;g->_col = Red;}// 叔叔不存在或者存在且为黑调整完,就不需要继续进行调整了break;}}else{node* u = g->_left;if (u && u->_col == Red){p->_col = u->_col = Black;g->_col = Red;// 继续往上处理cur = g;p = cur->_parent;}else {// g// u p// cif (cur == p->_right){// 左单旋RotateL(g);// 变色g->_col = Red;p->_col = Black;}// g// u p// celse {// 左右双旋RotateR(p);RotateL(g);// 变色cur->_col = Black;g->_col = Red;}// 叔叔不存在或者存在且为黑调整完,就不需要继续进行调整了break;}}}_root->_col = Black;}void inorder(){_inorder(_root);}
private:void _inorder(node* root){if (root == nullptr) return;_inorder(root->_left);cout << root->_val.first << " ";_inorder(root->_right);}void RotateR(node* parent){node* subl = parent->_left;node* sublr = subl->_right;node* grandfather = parent->_parent;parent->_left = sublr;if (sublr){sublr->_parent = parent;}subl->_right = parent;parent->_parent = subl;subl ->_parent = grandfather;if (_root == parent){if (grandfather->_left == parent){grandfather->_left = subl;}else{grandfather->_right = subl;}}else{_root = subl;}}void RotateL(node* parent){node* subr = parent->_right;node* subrl = subr->_left;node* grandfather = parent->_parent;parent->_right = subrl;if (subrl){subrl->_parent = parent;}subr->_left = parent;parent->_parent = subr;subr ->_parent = grandfather;if (_root != parent){if (grandfather->_left == parent){grandfather->_left = subr;}else{grandfather->_right = subr;}}else{_root = subr;}}protected:node* _root;
};相关文章:
C/C++ 进阶(6)红黑树
个人主页:仍有未知等待探索-CSDN博客 专题分栏:C 目录 一、概念 性质 二、操作 插入 情况一:cur为红、p为红、g为黑,如果u存在且为红 步骤: 情况二:cur为红、p为红、g为黑,如果u不存在或…...

【Vue】构建vuex-cart模块
说明:既然明确数据要存 vuex,建议分模块存,购物车数据存 cart 模块,将来还会有 user 模块,article 模块… 新建 store/modules/cart.js 挂载到 vuex 仓库上 store/cart.js import Vue from vue import Vuex from vu…...

如何成为嵌入式系统工程师?
各位朋友,如果你们有意向投身于嵌入式开发领域,那么强烈建议你们在软件和硬件两个方面均展开深入且全面的学习。 嵌入式计算机作为嵌入式系统的核心技术支撑,其是直接面向用户、产品以及应用的,无论是软件还是硬件方面都能发挥重要…...

【AI大模型】Transformers大模型库(七):单机多卡推理之device_map
目录 一、引言 二、单机多卡推理之device_map 2.1 概述 2.2 自动配置,如device_map"auto" 2.3 手动配置,如device_map"cuda:1" 三、总结 一、引言 这里的Transformers指的是huggingface开发的大模型库&#x…...

驱动代码编写(一)
驱动程序的作用 驱动程序是指与硬件设备和操作系统进行通信的软件。它的主要功能有以下几个方面: 提供硬件支持:驱动程序允许操作系统与硬件设备进行通信,以便正确地操作和控制硬件设备。它可以向操作系统提供有关硬件设备的各种信息&#x…...

Prompt-to-Prompt Image Editing with Cross Attention Control
Prompt-to-Prompt Image Editing with Cross Attention Control (P2P) Amir Hertz, Tel Aviv University, ICLR23, Paper, Code 1. 前言 编辑对这些生成模型来说是具有挑战性的,因为编辑技术的一个固有特性是保留大部分原始图像,而在基于文本的模型中…...

实验11 OSPF协议配置
实验11 OSPF协议配置 一、OSPF单区域配置(一)原理描述(二)实验目的(三)实验内容(四)实验配置(五)实验步骤 二、OSPF多区域配置(一)原理…...
ChatGPT-4o, 腾讯元宝,通义千问对比测试中文文化
国内的大模型应用我选择了国内综合实力最强的两个,一个是腾讯元宝,一个是通义千问。其它的豆包,Kimi,文心一言等在某些领域也有强于竞品的表现。 问一个中文文化比较基础的问题,我满以为中文文化chatGPT不如国内的大模型。可事实…...

node.js学习
node.js学习实操及笔记 温故node.js,node.js学习实操过程及笔记~ node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记 为什么学node.js 可以让别人访问我们编写的网页为后续的框架学习打下基础,三大框架vue react angular离不开node.js …...

python将一个图片雕刻镂空成二维码
本文使用创作助手。 要将一个图片雕刻镂空成二维码,你可以使用Python中的Pillow库来处理图像,并使用qrcode库来生成二维码。以下是一个示例代码,用于将图片雕刻镂空成二维码: import qrcode from PIL import Image# 打开待处理的…...
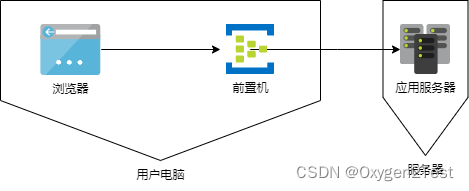
OS进程取样器OS Process Sampler执行CMD/Shell命令
Apache JMeter - Users Manual: Component Reference 1.背景 项目上最近需要测试一种很少用到的DICOM协议,但是网上资料很少,基本上可以总结为三种方案: 直接发送TCP 16进制数据包,但是参数化数据准备难度大通过开发封装jar包发送,需要开发组提供通过发送cmd命令给前置机…...

excel两个数据表格,怎样实现筛选的联动?
如图,想要通过处理器或者像素条件进行筛选,形成一个右边图2的对比表,如何实现实现联动显示呢? 这个在excel里可以借用数据透视表切片器来完成。步骤如下: 1.添加表 选中数据区域中任意一个单元格,点击 插…...

python,django好的get和post请求
获得get请求 df request.GET.get("dades")获得post请求 文件settings.py关闭csrf MIDDLEWARE [ ‘django.middleware.security.SecurityMiddleware’, ‘django.contrib.sessions.middleware.SessionMiddleware’, ‘django.middleware.common.CommonMiddleware’…...

volatile的用法
目录 前言 使用volatile的注意事项: 示例: 总结: 前言 在嵌入式C编程中,volatile是一个关键字,它用于告知编译器被修饰的变量可能会在程序的任何地方、任何时候被不可预见的、非程序本身控制的因素所改变。这通常…...

MySQL 与 PostgreSQL 关键对比二(SQL语法)
目录 1 详细示例 1.1自动增量列 1.2 字符串连接 1.3 JSON 支持 2 总结 MySQL 和 PostgreSQL 是两种流行的开源关系数据库管理系统(RDBMS)。尽管它们在许多方面相似,但在 SQL 语法和功能上存在一些显著差异。 以下SQL语句的执行如果需要开…...

徐州服务器租用该如何维护?
服务器能够帮助企业处理网络上大部分的数据和信息,在互联网行业中起着十分重要的作用,服务器的存在能够保障网站稳定的运行,主要是由内存、硬盘和处理器等组成,服务器除了进行正常的工作运行,还需要定期维护和管理&…...
—— 栈)
C++习题精选(4)—— 栈
目录 1. 最小栈2. 栈的压入弹出序列3. 逆波兰表达式求值 1. 最小栈 题目描述:设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。实现 MinStack 类: MinStack() 初始化堆栈对象。 void push(int val) 将元素…...
)
Web前端ES6-ES13笔记合集(下)
#### 五.ES10新特性 ##### 1. Object.fromEntries > Object.fromEntries()方法允许你轻松地将键值对列表转换为对象 js const arr [["name", "kerwin"], ["age", 100]]; console.log(Object.fromEntries(arr))//{name: kerwin, age: 100} …...

我要成为算法高手-双指针篇
目录 什么是双指针?问题1:移动零问题2:复写零问题3:快乐数问题4:盛最多水的容器问题5:有效三角形个数问题6:查找总价格和为目标值的两个商品(两数之和)问题7:三数之和问题8:四数之和…...
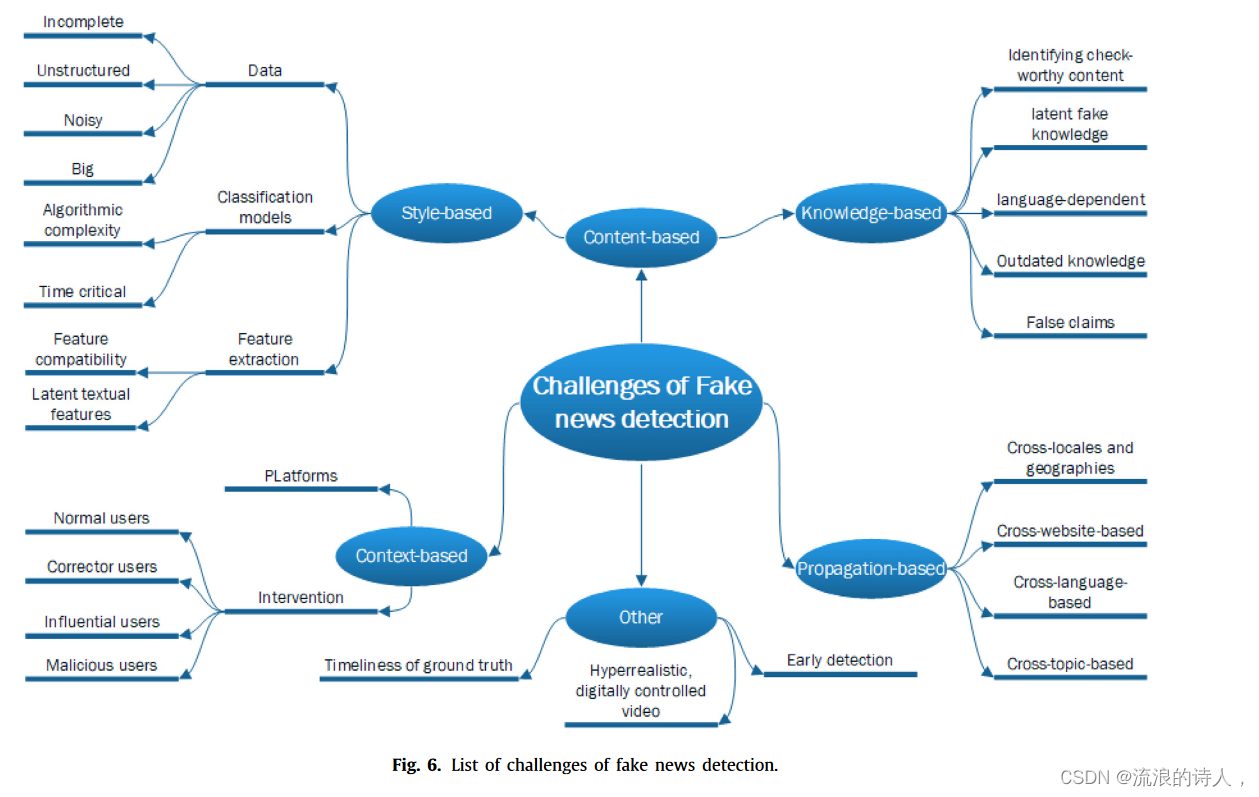
Fake news detection: A survey of graph neural network methods
abstract 各种社交网络的出现产生了大量的数据。捕获、区分和过滤真假新闻的有效方法变得越来越重要,特别是在 COVID-19 大流行爆发之后。本研究对假新闻检测系统的图神经网络 (GNN) 的现状和挑战进行了多方面、系统的回顾,并概述了使用 GNN 实现假新闻…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...