当前位置： 首页 > news >正文

数值计算精度问题(浮点型和双整型累加精度测试)

news 2026/5/13 18:49:40

这篇博客介绍双整型和浮点数累加精度问题，运动控制轨迹规划公式有大量对时间轴的周期累加过程,如果我们采用浮点数进行累加，势必会影响计算精度。速度的不同 进一步影响位置积分运算。轨迹规划相关问题请参考下面系列文章，这里不再赘述：

1、博途PLC 1200/1500PLC S型速度曲线变频器控制应用

博途PLC1200/1500PLC S型速度曲线变频器控制应用(SCL完整源代码)_s曲线scl程序-CSDN博客文章浏览阅读4.1k次，点赞3次，收藏12次。PLC运动控制基础系列之梯形速度曲线，可以参看下面这篇博客：PLC运动控制基础系列之梯形速度曲线_RXXW_Dor的博客-CSDN博客运动控制的梯形加减速大家应该很熟悉了，这篇博文属于基础概念性文章，陆续会更新和运动控制相关的内容，PLC运动控制算法讲解，分析。..._s曲线scl程序https://blog.csdn.net/m

相关文章：

数值计算精度问题(浮点型和双整型累加精度测试)

这篇博客介绍双整型和浮点数累加精度问题，运动控制轨迹规划公式有大量对时间轴的周期累加过程,如果我们采用浮点数进行累加，势必会影响计算精度。速度的不同 进一步影响位置积分运算。轨迹规划相关问题请参考下面系列文章，这里不再赘述： 1、博途PLC 1200/1500PLC S型速度曲…...

编程日记 2024/6/12 4:04:11

算法训练营day56

题目1&#xff1a;300. 最长递增子序列 - 力扣&#xff08;LeetCode&#xff09; class Solution { public:int lengthOfLIS(vector<int>& nums) {// dp数组含义是第i个数的严格递增子序列的长度// 内层的递推公式就是 取 0 到 i - 1之间最大的dp数组 然后 1vector…...

编程日记 2024/6/12 4:02:09

基于STM32的智能水产养殖系统（二）

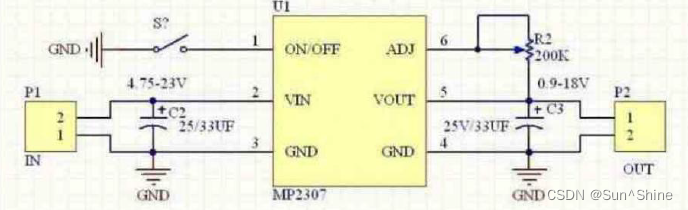
TPS5433IDR TPS5433IDR 是一款由德州仪器 (Texas Instruments) 生产的高效降压转换器&#xff08;Buck Converter&#xff09;。它能够将较高的输入电压转换为较低的输出电压&#xff0c;适用于各种电源管理应用。 主要特性 输入电压范围: 5.5V 至 36V输出电压范围: 0.9V 至 …...

编程日记 2024/6/12 3:58:05

[工具探索]富士mini90拍立得使用指南

文章目录 1. 基本功能介绍1.1 相机外观1.2 电池与胶片 2. 设置相机2.1 装入电池2.2 装入胶片 3. 拍摄模式3.1 标准模式3.2 儿童模式3.3 远景模式3.4 双重曝光模式3.5 Bulb&#xff08;B&#xff09;模式3.6 **派对模式**3.7 微距模式3.8 **亮度模式**3.9 **定时拍摄模式**3.10 …...

编程日记 2024/6/12 3:57:04

VMware导入小白分享的MacOS版本之后，无法开机的解决方案

前言 这段时间陆续有小伙伴找到小白&#xff0c;说&#xff1a;导入小白分享的MacOS版本之后&#xff0c;出现无法开机的问题。 遇到这个问题&#xff0c;并不是说明分享版本有问题&#xff0c;因为大部分小伙伴导入之后都没有出现类似的问题&#xff0c;都是导入之后开机&…...

编程日记 2024/6/12 3:56:03

【CSAPP导读】导论

目录 &#x1f308; 前言&#x1f308; &#x1f4c1; 书籍介绍 &#x1f4c1; 阅读路线 &#x1f4c1; 总结 &#x1f308; 前言&#x1f308; 《深入理解计算机系统》书籍是由布赖恩特(Bryant,R.E.)著的一本经典计算机科学教材&#xff0c;常被简称为"CSAPP"&a…...

编程日记 2024/6/12 3:55:02

“新E代弯道王”MAZDA EZ-6亮相2024重庆国际车展

6月7日-6月16日&#xff0c;第二十六届重庆国际车展隆重开幕&#xff0c;合资品牌首款基于纯电平台的新能源轿车MAZDA EZ-6&#xff08;以下称EZ-6&#xff09;领衔长安马自达全系车型亮相N8馆T01展台。车展期间&#xff0c;重庆及周边地区的马自达用户、粉丝、车友可前往长安马…...

编程日记 2024/6/12 3:52:57

【lesson11】客户端backUp类的实现

文章目录 成员变量成员函数backUpgetFileIdentifierisNeedUploadupLoadRunMoudle 成员变量 private:std::string _back_dir;//备份文件夹路径名dataManager* _data;//dataManager指针对象成员函数 backUp backUp(const std::string& back_dir, const std::string& b…...

编程日记 2024/6/12 3:50:54

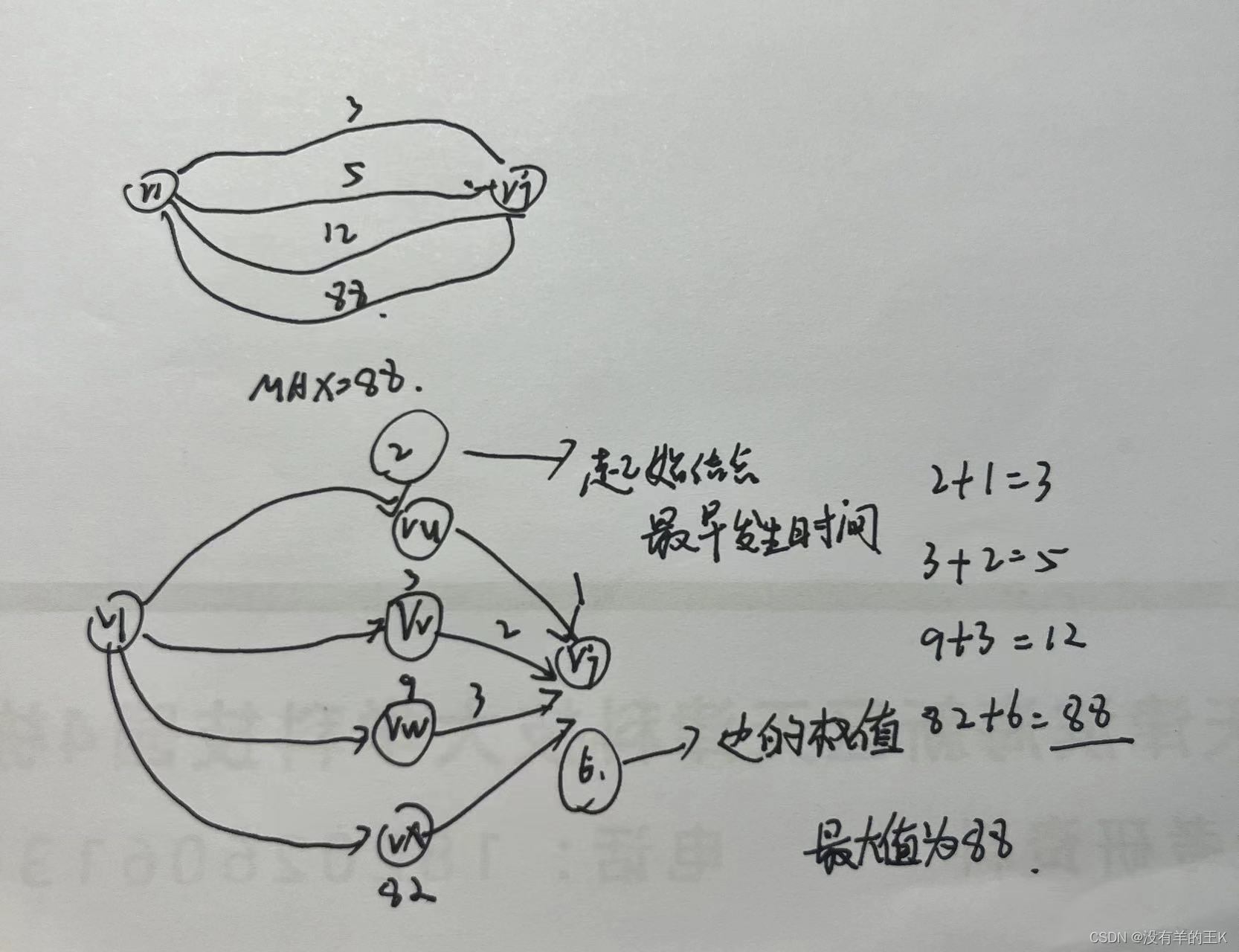
数据结构--关键路径

事件v1-表示整个工程开始&#xff08;源点&#xff1a;入度为0的顶点&#xff09; 事件v9-表示整个工程结束&#xff08;汇点&#xff1a;出度为0的顶点&#xff09; 关键路径&#xff1a;路径长度最长的路径 求解关键路径问题&#xff08;AOE网&#xff09; 定义四个描述量 …...

编程日记 2024/6/12 3:48:53

SSTI注入漏洞

SSTI注入漏洞 1.SSTI注入概述2.SSTI检测工具3.SSTI利用方法Java基本FreeMarker (Java)ThymeleafSpring Framework (Java)Spring视图操作&#xff08;Java&#xff09;Smarty (PHP)Twig (PHP)Jade (NodeJS)NUNJUCKS (NodeJS)ERB (Ruby)Jinja2 (Python)Mako (Python)ASP 1.SSTI注…...

编程日记 2024/6/12 3:47:52

Day11 - Day15

Day11 - Day15 Day11&#xff08;1998年Text1&#xff09; Perhaps it is humankind’s long suffering at the mercy of flood and drought that makes the idea of forcing the waters to do our bidding so fascinating. 也许正是人类长期在洪水和干旱支配下所遭受的苦难&a…...

编程日记 2024/6/12 3:46:51

启航信息学奥林匹克：青少年NOI学习路线与策略指南

在全球范围内&#xff0c;信息学奥林匹克竞赛&#xff08;NOI&#xff09;不仅是青少年展示编程和算法能力的舞台&#xff0c;更是未来计算机科学家和工程师的摇篮。本文将为志在参加NOI的青少年们提供一条清晰的学习路线和实用的建议&#xff0c;帮助你们在这条充满挑战与机遇…...

编程日记 2024/6/12 3:45:50

易舟云财务软件：数字化时代的财务管家

在数字化浪潮的推动下&#xff0c;财务软件成为了企业提升财务管理效率、实现数字化转型的关键工具。易舟云财务软件&#xff0c;正是这样一款深受企业喜爱的财务管理系统。本文将带你详细了解易舟云财务软件的特点、版本区别以及如何使用它来优化财务工作。 易舟云财务软件的特…...

编程日记 2024/6/12 3:43:48

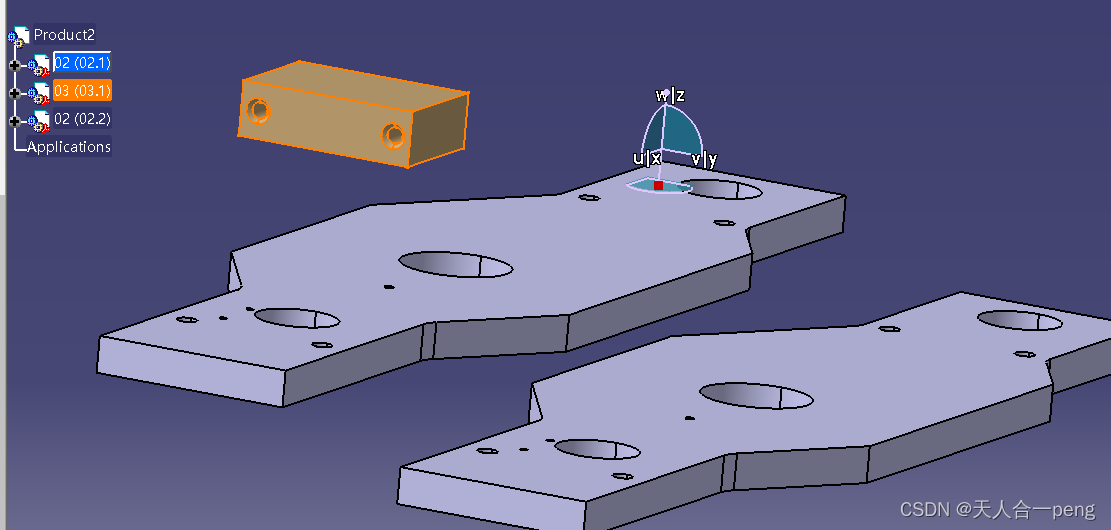
catia零件装配中通过指南针移动零件

1 将零件导入进来后 2 把指南针移动到零件上 具体移动哪个可以通过模型树点击选中&#xff0c;选中那个就可以移动那个。 这种情况需要注意的是 需要双击选择要移动零件的父节点 如下图&#xff0c;Product2蓝色表示是激活的&#xff0c;这样才可以单击选中下面的零件后通过…...

编程日记 2024/6/12 3:42:45

如何使用免费的 Instant Data Scraper快速抓取网页数据

Instant Data Scraper 是一款非常简单易用的网页数据爬虫工具&#xff0c;你不需要任何代码知识&#xff0c;只需要点几下鼠标&#xff0c;就可以把你想要的数据下载到表格里面。以下是详细的使用步骤&#xff1a; 第一步&#xff1a;安装 Instant Data Scraper 打开谷歌浏览…...

编程日记 2024/6/12 3:39:42

【仿真建模-anylogic】事件之手动定时触发

Author&#xff1a;赵志乾 Date&#xff1a;2024-06-11 Declaration&#xff1a;All Right Reserved&#xff01;&#xff01;&#xff01; 问题&#xff1a;建模过程中经常遇到需要临时规划特定逻辑执行时机的场景&#xff1b; 解决方案&#xff1a;在Event的User Control模…...

编程日记 2024/6/12 3:37:40

ElasticSearch学习笔记之三：Logstash数据分析

第3章 Logstash数据分析 Logstash使用管道方式进行日志的搜集处理和输出。有点类似*NIX系统的管道命令 xxx | ccc | ddd&#xff0c;xxx执行完了会执行ccc&#xff0c;然后执行ddd。 在logstash中&#xff0c;包括了三个阶段: 输入input --> 处理filter&#xff08;不是必须…...

编程日记 2024/6/12 3:35:38

求职力扣刷题DAY20--二叉树 part06

20 654. 最大二叉树 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点&#xff0c;其值为 nums 中的最大值。递归地在最大值 左边 的 子数组前缀上 构建左子树。递归地在最大值 右边 的 子数组后缀上 构建右子树。 返回 n…...

编程日记 2024/6/12 3:34:37

Error:Kotlin: Module was compiled with an incompatible version of Kotlin.

一、问题&#xff1a;运行spring boot项目时&#xff0c;idea报出错误&#xff1a;时提示报错如下图&#xff1a; 错误代码&#xff1a; Error:Kotlin: Module was compiled with an incompatible version of Kotlin. The binary version of its metadata is 1.6.0, expected …...

编程日记 2024/6/12 3:33:34

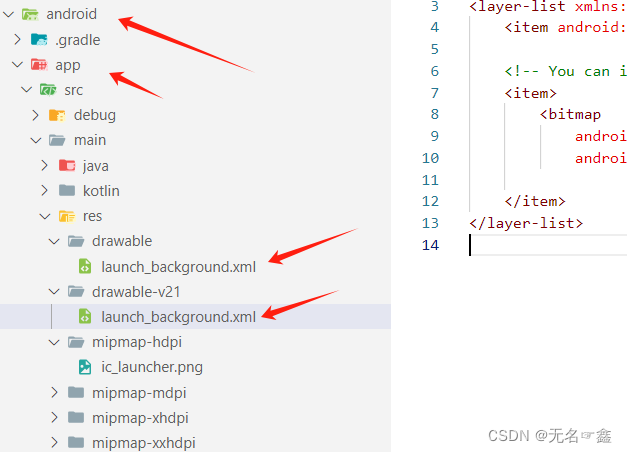
关于flutter 启动 页面加载空白（三四秒空白页面）

一:可以在 对应的xml配置启动动画 <item><bitmapandroid:gravity"center"android:src"mipmap/ic_launcher" /></item> 二&#xff1a;以下是对应的文件目录 注意事项&#xff1a;俩处xml都配置一下&#xff0c;配置一样就可以了...

编程日记 2024/6/12 3:31:31

DeepSeek总结的DwarfStar 4：专为 DeepSeek V4 Flash 设计的小型原生推理引擎

来源&#xff1a;https://github.com/antirez/ds4 DwarfStar 4 DwarfStar 4 是一个为 DeepSeek V4 Flash 设计的小型原生推理引擎。它是有意限定了范围的&#xff1a;不是通用的 GGUF 运行器&#xff0c;不是其他运行时的封装器&#xff0c;也不是一个框架。其主要路径是一个…...

编程新知 2026/5/13 17:34:23

React 18 + Vite + Tailwind CSS 构建现代化SaaS落地页实战

1. 项目概述与设计思路最近在做一个保险科技&#xff08;InsurTech&#xff09;相关的概念项目&#xff0c;需要为这个名为“Insura”的SaaS平台打造一个现代化的落地页&#xff08;Landing Page&#xff09;。这个页面的核心目标很明确&#xff1a;向潜在客户&#xff08;主要…...

编程新知 2026/5/13 17:04:52

Allegro丝印层加汉字和防静电标识？我找到了比自带功能更香的免费Skill工具

Allegro丝印层高效处理方案&#xff1a;汉字与防静电标识的终极实践指南 在PCB设计的最后阶段&#xff0c;丝印层的处理往往成为工程师们头疼的问题。尤其是当设计需要添加中文注释、企业标识或行业标准符号&#xff08;如防静电警告标志&#xff09;时&#xff0c;Allegro原生…...

编程新知 2026/5/13 16:40:43

建立个人学习SOP：信息输入、消化吸收与输出实践

对于软件测试从业者而言&#xff0c;技术迭代的速度往往快于岗位技能的沉淀周期。从自动化框架的百花齐放到 AI 驱动测试的兴起&#xff0c;从微服务架构下的契约测试到混沌工程在稳定性领域的渗透&#xff0c;测试人员需要持续吸收新知识&#xff0c;却又极易陷入“学得越多&a…...

编程新知 2026/5/13 16:27:19

Stata 数据处理实战：时间序列数据的日期转换与聚合

1. 时间序列数据处理的常见痛点 刚接触时间序列分析的朋友们&#xff0c;经常会遇到这样的困扰&#xff1a;从Excel导入的数据明明是日期格式&#xff0c;到了Stata里却变成了看不懂的字符&#xff1b;想按周汇总销售数据&#xff0c;却发现系统根本不认识"2023-W15"…...

编程新知 2026/5/13 15:18:09

cPanel三连漏洞CVE-2026-29201/29202/29203深度解析：150万服务器面临全面接管危机

一、事件引言&#xff1a;2026年主机行业最大安全地震 2026年5月8日&#xff0c;全球市场份额第一的服务器管理面板cPanel & WHM 发布紧急安全公告&#xff0c;一次性披露三个高危安全漏洞&#xff08;CVE-2026-29201/29202/29203&#xff09;。这组被安全界称为"cPa…...

编程新知 2026/5/13 14:57:45

OBS Source Record插件完全掌握指南：实现多源独立录制的终极解决方案

OBS Source Record插件完全掌握指南&#xff1a;实现多源独立录制的终极解决方案 【免费下载链接】obs-source-record 项目地址: https://gitcode.com/gh_mirrors/ob/obs-source-record 你是否曾经在直播或录制视频时&#xff0c;想要单独保存某个特定的画面源&#xf…...

编程新知 2026/5/13 14:32:58

Axure中文汉化终极指南：3分钟搞定英文界面，让原型设计更顺手

Axure中文汉化终极指南&#xff1a;3分钟搞定英文界面&#xff0c;让原型设计更顺手 【免费下载链接】axure-cn Chinese language file for Axure RP. Axure RP 简体中文语言包。支持 Axure 11、10、9。不定期更新。 项目地址: https://gitcode.com/gh_mirrors/ax/axure-cn …...

编程新知 2026/5/13 13:54:51

构建自动化编译系统：Makefile递归遍历与智能目录生成实践

1. 为什么需要自动化编译系统 如果你曾经维护过一个包含几十个源文件的中大型C/C项目&#xff0c;肯定经历过这样的痛苦&#xff1a;每次新增一个源文件&#xff0c;都要手动修改Makefile&#xff1b;项目结构调整时&#xff0c;编译规则需要全部重写&#xff1b;不同模块之间的…...

编程新知 2026/5/13 12:58:59

告别云服务器：手把手教你用QEMU在Ubuntu 18.04上搭建专属内核调试环境

从零构建QEMU内核调试环境&#xff1a;Ubuntu 18.04下的UEFI开发实战手册 当深夜的调试灯亮起&#xff0c;你是否还在为云服务器高昂的费用和网络延迟苦恼&#xff1f;本文将带你用一台普通Ubuntu机器&#xff0c;打造媲美物理机的内核开发环境。不同于常规教程&#xff0c;我…...

编程新知 2026/5/13 12:18:01