概率分析和随机算法
目录
雇佣问题
概率分析
随机算法
生日悖论
随机算法
概率分析
球与箱子
总结
雇佣问题
有n个候选人面试,如果面试者比目前雇佣者的分数高,评价更好,那么就辞掉当前雇佣者,而去聘用面试者,否则继续面试新的候选人。面试完n个人结束。
best为到i个候选人中最佳面试者, a数组时候选人名单。
起始条件:best= a[0]; 聘用第一个面试者。
保持:if(best < a[i]) best = a[i]; 聘用面试者。
终止条件:当i == n 时,迭代终止。
代码:
#include "stdio.h"void main() {int best = 0;int n = 10;int a[10] = {0};for (size_t i = 0; i < n; i++){scanf("%d", &a[i]);if(best < a[i]) {best = a[i];}}}
算法分析:
| 代码 | 代价 | |
| 面试 | scanf("%d", &a[i]); | C1 |
| 雇佣 | best = a[i]; | C2 |
假如面试过程中有m个人被雇佣,则总的代价=O(c1*n + c2*m).(0<m<=n)
最坏情况分析:
m=n时,总的代价最大,此时为O(c1*n + c2*n). 由于c1远小于c2,因此总代价为O(c2*n).
平均情况分析:
求平均情况就是求m=1~n的所有可能的均值。在数学中求平均值可以转化为求一个参量的期望。那如何求这个期望值呢?
概率分析
一个面试者是否面试通过服从二项分布。
m个雇佣者的被雇佣的概率
| Xi | 0 | 第1个 | 第2个 | 第n个 |
| P | 0 | 1 | 1/2 | 1/n |
E[X] = E[X1] + E[X2] + … +E[Xn] = 1+1/2+…+1/n = lnx + O(1).
随机算法
代码:
#include "stdio.h"
#include "math.h"
#include <time.h>void permute_by_sorting(int p[10], int a[10]);
void swap(int *a, int *b);
void main() {int best = 0;int rank = 0;int n = 10;int a[10] = {5,2,3,1,4,9,8,10,7,6};int p[10] = {0};permute_by_sorting(p, a);for (size_t i = 0; i < n; i++){if(best < a[i]) {best = a[i];rank = i;}}printf("\nThe best hired man is %dth %d", rank, best);}void permute_by_sorting(int p[10], int a[10]) {int count = 10;srand(time(0));for (size_t i = 0; i < count; i++){p[i] = rand()%1000;printf("%d, ", p[i]);}printf("\n");for (size_t i = 0; i < count; i++){for (size_t j = i; j < count; j++){if(p[i] > p[j]) {swap(&p[i], &p[j]);swap(&a[i], &a[j]);}}printf("%d ", a[i]);}}void swap(int *a, int *b) {int temp;temp = *a;*a = *b;*b = temp;
}
输出结果:

随机排列数列:
可以从输出结果看出,每次出现的优先级的数列不一样,是随机的。样本空间为n!种排列方式,也就是全排列方式,这样就形成了随机算法了,可以使用概率分析算法的性能,每次出现的排列的概率都是1/n!。
以下两行代码能够执行到的次数m的期望E(X)= O(lnx).
best = a[i];rank = i;
生日悖论
问题描述:一个屋子里,必须要有多少人以上,才可以至少有生日相同的两个人?
随机算法
代码
#include "stdio.h"
#include "math.h"
#include <time.h>#define PERSON_NUM 40
void permute_by_sorting(int p[10]);void main() {int same_birthday_p1 = -1;int same_birthday_p2 = -1;int n = PERSON_NUM;int p[PERSON_NUM] = {0};permute_by_sorting(p);for (size_t i = 0; i < n; i++){for (size_t j = i+1; j < n; j++){if(p[j] == p[i]) {same_birthday_p1 = i;same_birthday_p2 = j;break;}}}printf("\nThe best hired man is %d and %d", same_birthday_p1, same_birthday_p2);}void permute_by_sorting(int p[PERSON_NUM]) {int count = PERSON_NUM;srand(time(0));for (size_t i = 0; i < count; i++){p[i] = rand()%365;printf("%d, ", p[i]);}}
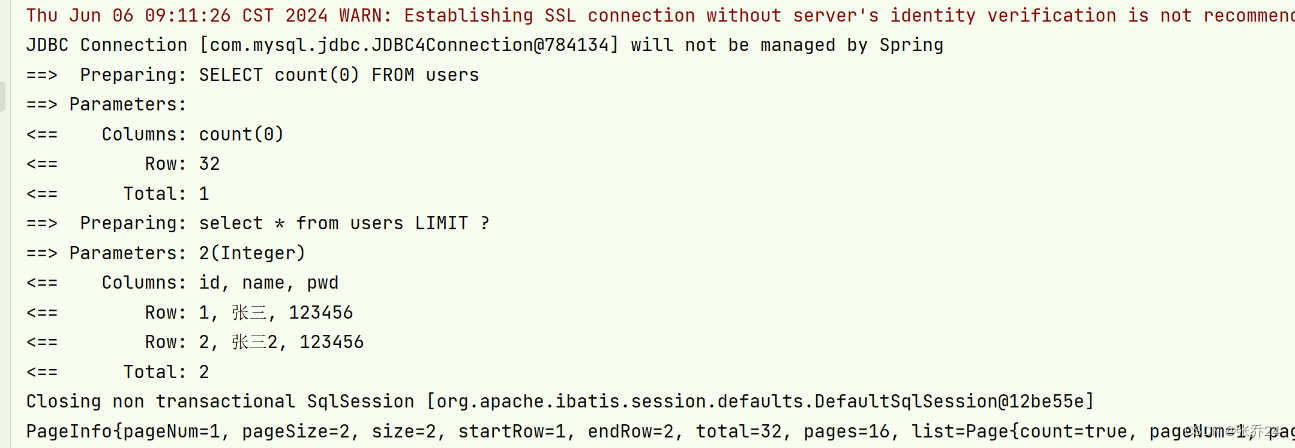
PERSON_NUM设为10和40的输出结果:


概率分析
i人和j人两个生日相等且在r日的概率 P[r]= 1/365*1/365. 令n=365. P[r]=1/n*n.
而i人和j人生日相等的情况有1,2,3…,365种,所以P = P[r]*n = 1/n.
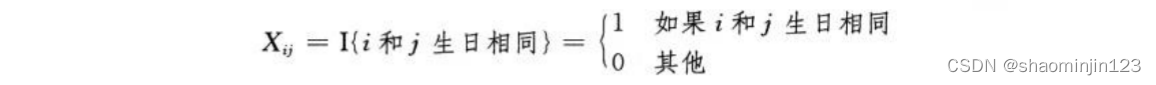
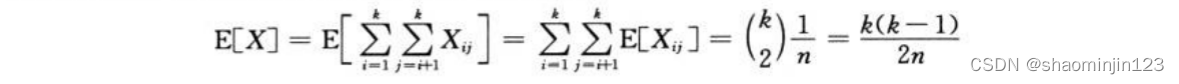
以下的代码中,最后执行了判断语句中的语句时,有X个人相同的期望值为E[X].
E[X]= k(k-1)/(2*n) (PERSON_NUM = k, n = 365).
if(p[j] == p[i]) {same_birthday_p1 = i;same_birthday_p2 = j;break;
}
我在代码中将PERSON_NUM设为10和40的输出结果
| PERSON_NUM | E(X) | 结果 |
| 10 | 0.1232876712328767 | 没有相同生日的人 |
| 40 | 0.4931506849315068 | 有相同生日的人 |
房间中人数为40人时,出现生日相同的期望为1/2,而10人时期望仅为1/10.我输入两次得出生日的结果也与概率模型预期匹配。
球与箱子
问题描述:有b个箱子,往一个指定的箱子中投入球的概率为1/b,投出n个相同的求,指定箱子中有k个球,求k值的期望值。
k正好符合二项分布,b(n,1/b); 所以k的期望值E(K) = n/b.

总结
本文以雇佣问题,生日悖论和球与箱子问题入手,着重讲述如何使用概率方法分析随机算法。
相关文章:

概率分析和随机算法
目录 雇佣问题 概率分析 随机算法 生日悖论 随机算法 概率分析 球与箱子 总结 雇佣问题 有n个候选人面试,如果面试者比目前雇佣者的分数高,评价更好,那么就辞掉当前雇佣者,而去聘用面试者,否则继续面试新的候…...

15_2 Linux Shell基础
15_2 Linux Shell基础 文章目录 15_2 Linux Shell基础[toc]1. shell基本介绍1.1 什么是shell1.2 shell使用方式1.3 脚本的执行方式1.4 脚本练习 2. 变量的种类2.1 自定义变量2.2 环境变量,由系统提前定义好,使用时直接调用2.3 位置变量与预定变量2.4 变量…...
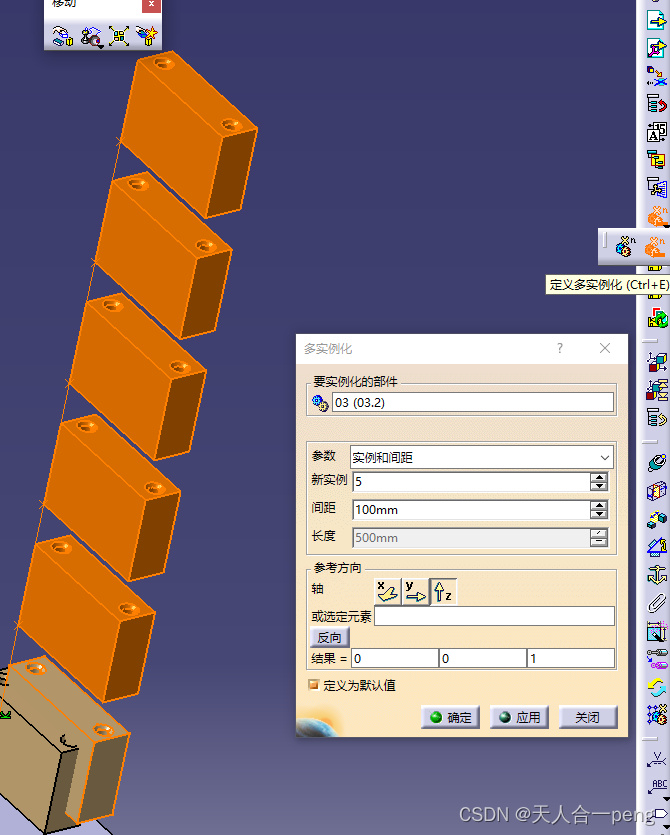
Catia装配体零件复制
先选中要复制的零件 然后选中复制到的父节点才可以。 否则 另外一种方法是多实例化...

实用小工具-python esmre库实现word查找
python esmre库实现word查找 前言: 在文本中匹配特定的字符串,一般可以用普通的字符串匹配算法,KMP算法; python中提供了一个库,esmre, 通过预先将字符串存到esm对象中,利用这些字符串从候选的字符串中进行…...
SSM框架整合,内嵌Tomcat。基于注解的方式集成
介绍: SSM相信大家都不陌生,在spring boot出现之前,SSM一直是Java在web开发中的老大哥。现在虽说有了spring boot能自动整合第三方框架了,但是现在市面上任然有很多老项目是基于SSM技术的。因此,能熟练掌握SSM进行开发…...
)
系统架构设计师【论文-2016年 试题4】: 论微服务架构及其应用(包括写作要点和经典范文)
论微服务架构及其应用(2016年 试题4) 近年来,随着互联网行业的迅猛发展,公司或组织业务的不断扩张,需求的快速变化以及用户量的不断增加,传统的单块(Monolithic)软件架构面临着越来越多的挑战,…...

面试题:String 、StringBuffer 、StringBuilder的区别
String、StringBuffer、和StringBuilder都是用于处理字符串的操作类,但它们之间存在一些关键性的差异: 1.不可变性与可变性: String:字符串常量,是不可变的。一旦创建,其内容就不能被改变。对字符串的任何…...

TLS指纹跟踪网络安全实践(C/C++代码实现)
TLS指纹识别是网络安全领域的重要技术,它涉及通过分析TLS握手过程中的信息来识别和验证通信实体的技术手段。TLS(传输层安全)协议是用于保护网络数据传输的一种加密协议,而TLS指纹则是该协议在实际应用中产生的独特标识࿰…...
小白学RAG:大模型 RAG 技术实践总结
节前,我们组织了一场算法岗技术&面试讨论会,邀请了一些互联网大厂朋友、今年参加社招和校招面试的同学。 针对大模型技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何准备面试攻略、面试常考点等热门话题进行了深入的讨论。 汇总合集…...
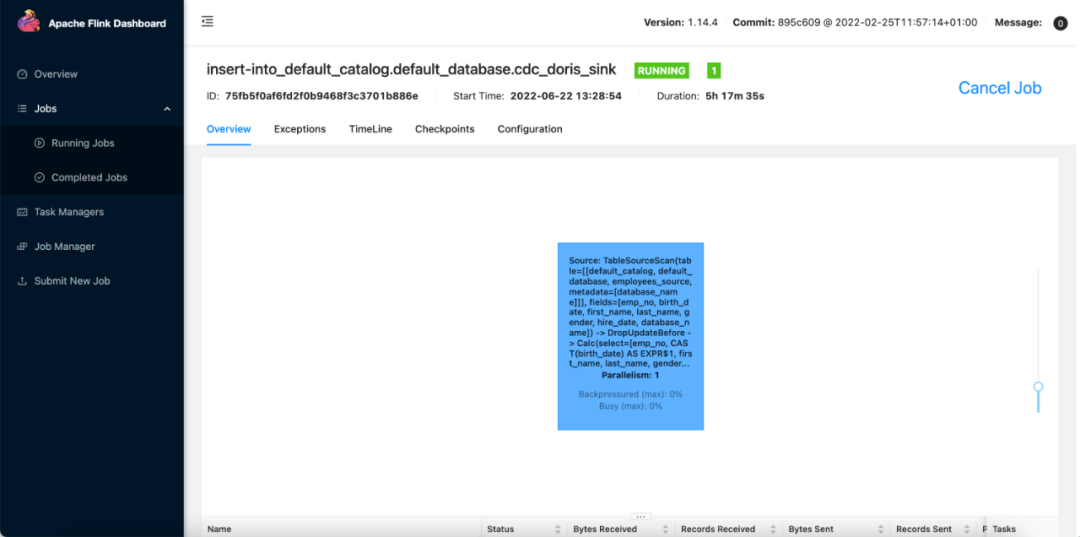
Doris Connector 结合 Flink CDC 实现 MySQL 分库分表
1. 概述 在实际业务系统中为了解决单表数据量大带来的各种问题,我们通常采用分库分表的方式对库表进行拆分,以达到提高系统的吞吐量。 但是这样给后面数据分析带来了麻烦,这个时候我们通常试将业务数据库的分库分表同步到数据仓库时&#x…...

ModbusTCP、TCP/IP都走网线,一样吗?
在现代通信技术中,Modbus/TCP和TCP/IP协议是两种广泛应用于工业自动化和网络通信领域的协议。尽管它们都运行在网线上,但它们在设计、结构和应用场景上有着明显的区别。 Modbus/TCP协议是什么 Modbus/TCP是一种基于TCP/IP的应用层协议,它是Mo…...
|Spring Boot中获取HTTP请求头(Header)内容的详细解析)
网络学习(13)|Spring Boot中获取HTTP请求头(Header)内容的详细解析
文章目录 方法一:使用HttpServletRequest实现原理代码示例优点缺点适用场景 方法二:使用RequestContextHolder实现原理代码示例优点缺点适用场景 方法三:使用RequestHeader注解实现原理代码示例优点缺点适用场景 总结 在Spring Boot应用中&am…...

【漏洞复现】宏景eHR pos_dept_post SQL注入漏洞
0x01 产品简介 宏景eHR人力资源管理软件是一款人力资源管理与数字化应用相融合,满足动态化、协同化、流程化、战略化需求的软件。 0x02 漏洞概述 宏景eHR pos_dept_post 接囗处存在SQL注入漏洞,未经过身份认证的远程攻击者利用此漏洞执行任意SQL指令,…...

82. 删除排序链表中的重复元素 and II
链接直达: 保留重复元素 不保留重复元素 题目: 1: 给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表 。示例 1:输入:head [1,1,2] 输出:[1…...

C++ 判断目标文件是否被占用(独占)(附源码)
在IM软件中发起文件发送时,如果要发送的是某word文件,并且该word文件被office打开,则会提示文件正在被占用无法发送,如下所示: 那文件被占用到底是如何判断出来的呢?其实很简单,调用系统API函数CreateFile,打开该文件(OPEN_EXISTING),传入FILE_SHARE_READ共享读标记…...

计划任务 之 一次性的计划任务
计划任务 作用:定时自动完成特定的工作 计划任务的分类: (1)一次性的计划任务 例如下周三对系统的重要文件备份一次 (2)周期性重复计划任务 例如每天晚上12:00备份一次 一次性的任务计划:…...
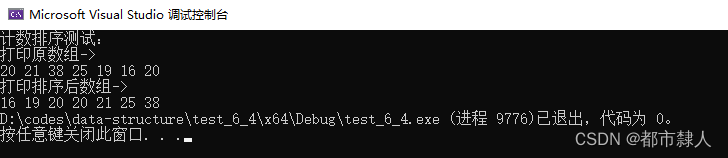
非比较排序之计数排序
目录 一、什么是计数排序 二、思路 三、代码实现 一、什么是计数排序 计数排序是一种非比较型的排序算法,它通过统计待排序数据中每个元素出现的次数,然后根据这个次数来进行排序。计数排序的具体步骤如下: 首先找出待排序数据中的最大值…...

Django路由与会话深度探索:静态、动态路由分发,以及Cookie与Session的奥秘
系列文章目录 Django入门全攻略:从零搭建你的第一个Web项目Django ORM入门指南:从概念到实践,掌握模型创建、迁移与视图操作Django ORM实战:模型字段与元选项配置,以及链式过滤与QF查询详解Django ORM深度游ÿ…...
第7章 用户输入和 while 循环
第7章 用户输入和 while 循环 7.1 函数 input()的工作原理7.1.1 编写清晰的程序7.1.2 使用 int()来获取数值输入7.1.3 求模运算符 7.2 while 循环简介7.2.1 使用 while 循环7.2.2 让用户选择何时退出7.2.3 使用标志7.2.4 使用 break 退出循环7.2.5 在循环中使用 continue7.2.6 …...
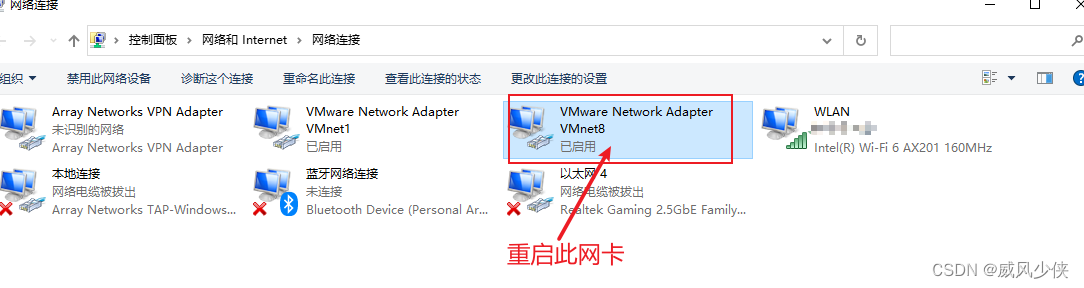
xshell远程无法链接上VM的centos7
1、现象如下, 2.1解决办法:查证后发现这个默认的设置为vmnet0 2.2解决办法:重启win10的虚拟机网卡(先禁用再启用) 3.参考文章:Xshell连接不上虚拟机centos7_centos7的nat模式可以ping通网络,但是用xshell连…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
