【Java刷题】二叉树
- 相同的树
public boolean isSameTree(TreeNode p, TreeNode q) {if(p == null && q == null) {return true;} else if(p != null && q != null) {if(p.val != q.val) {return false;} else {return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);}}return false;
}
- 另一棵树的子树
public boolean isSameTree(TreeNode p, TreeNode q) {if(p == null && q == null) {return true;} else if(p != null && q != null) {if(p.val != q.val) {return false;} else {return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);}}return false;
}
public boolean isSubtree(TreeNode root, TreeNode subRoot) {if(root == null) {return false;}return isSameTree(root, subRoot) || isSubtree(root.left, subRoot) || isSubtree(root.right, subRoot);
}
- 翻转二叉树
public TreeNode invertTree(TreeNode root) {if(root == null) {return null;}TreeNode left = invertTree(root.left);TreeNode right = invertTree(root.right);root.left = right;root.right = left;return root;
}
- 平衡二叉树
// 方式一
public int getHeight(TreeNode root) {if(root == null) {return 0;}return 1 + Math.max(getHeight(root.left), getHeight(root.right));
}
public boolean isBalanced(TreeNode root) {if(root == null) {return true;}if( Math.abs(getHeight(root.left) - getHeight(root.right)) > 1 ) {return false;}return isBalanced(root.left) && isBalanced(root.right);
}// 方式二 - 优化
public int getHeight(TreeNode root) {if(root == null) {return 0;}int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);if( leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1 ) {return -1;}return 1 + Math.max(leftHeight, rightHeight);
}
public boolean isBalanced(TreeNode root) {return getHeight(root) >= 0;
}
- 对称二叉树
public boolean isSymmetricHelper(TreeNode left, TreeNode right) {if(left == null && right == null) {return true;} else if(left != null && right != null) {if(left.val != right.val) {return false;} else {return isSymmetricHelper(left.left, right.right) && isSymmetricHelper(left.right, right.left);}}return false;
}
public boolean isSymmetric(TreeNode root) {if(root == null) {return true;}return isSymmetricHelper(root.left, root.right);
}
- 二叉树遍历
class TreeNode {public char val;public TreeNode left;public TreeNode right;public TreeNode(char val) {this.val = val;}
}public class Main {public static int i;public static TreeNode createTree(String str) {TreeNode root = null;char c = str.charAt(i++);if(c != '#') {root = new TreeNode(c);root.left = createTree(str);root.right = createTree(str);}return root;}public static void inorder(TreeNode root) {if(root == null) {return;}inorder(root.left);System.out.print(root.val + " ");inorder(root.right);}public static void main(String[] args) {Scanner in = new Scanner(System.in);while (in.hasNextLine()) {String str = in.nextLine();i = 0;TreeNode root = createTree(str);inorder(root);System.out.println();}}
}
- 二叉树的层序遍历
public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> ret = new ArrayList<>();if(root == null) {return ret;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {int size = queue.size();List<Integer> row = new ArrayList<>();while (size > 0) {TreeNode peek = queue.peek();if(peek.left != null) {queue.offer(peek.left);}if(peek.right != null) {queue.offer(peek.right);}row.add(queue.remove().val);--size;}ret.add(row);}return ret;
}
- 二叉树的最近公共祖先
// 方式一
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(root == null) return root;if(root == p || root == q) {return root;}TreeNode left = lowestCommonAncestor(root.left, p, q);TreeNode right = lowestCommonAncestor(root.right, p, q);if(left != null && right != null) {return root;} else if(left != null) {return left;} else {return right;}
}// 方式二
public boolean lowestCommonAncestorHelper(TreeNode root, TreeNode tofind, Stack<TreeNode> stack) {if(root == null) return false;stack.push(root);if(root == tofind) return true;if(lowestCommonAncestorHelper(root.left, tofind, stack) || lowestCommonAncestorHelper(root.right, tofind, stack)) {return true;} else {stack.pop();return false;}
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {Stack<TreeNode> stack1 = new Stack<>();Stack<TreeNode> stack2 = new Stack<>();lowestCommonAncestorHelper(root, p, stack1);lowestCommonAncestorHelper(root, q, stack2);while(stack1.size() > stack2.size()) {stack1.pop();}while(stack1.size() < stack2.size()) {stack2.pop();}while(stack1.peek() != stack2.peek()) {stack1.pop();stack2.pop();}return stack1.peek();
}
- 从前序与中序遍历序列构造二叉树
public int step = 0;
public TreeNode buildTreeHelper(int[] preorder, int[] inorder, int start, int end) {if(start > end) return null;TreeNode root = new TreeNode(preorder[step++]);int i = 0;for ( ; i <= end; i++) {if (inorder[i] == root.val) {break;}}root.left = buildTreeHelper(preorder, inorder, start, i - 1);root.right = buildTreeHelper(preorder, inorder, i + 1, end);return root;
}
public TreeNode buildTree(int[] preorder, int[] inorder) {return buildTreeHelper(preorder, inorder, 0, inorder.length - 1);
}
- 从中序与后序遍历序列构造二叉树
public int step;
public TreeNode buildTreeHelper(int[] postorder, int[] inorder, int start, int end) {if(start > end) return null;TreeNode root = new TreeNode(postorder[step--]);int i = 0;for ( ; i <= end; i++) {if (inorder[i] == root.val) {break;}}// 构建顺序相对前序 交换一下root.right = buildTreeHelper(postorder, inorder, i + 1, end);root.left = buildTreeHelper(postorder, inorder, start, i - 1);return root;
}
public TreeNode buildTree(int[] inorder, int[] postorder) {step = postorder.length - 1;return buildTreeHelper(postorder, inorder, 0, inorder.length - 1);
}
- 根据二叉树创建字符串
public String tree2str(TreeNode root) {if(root == null) return "";StringBuilder str = new StringBuilder();str.append(root.val);if(root.left != null || root.right != null) {str.append('(');str.append(tree2str(root.left));str.append(')');}if(root.right != null) {str.append('(');str.append(tree2str(root.right));str.append(')');}return str.toString();
}
- 二叉树的前序遍历
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();if (root == null) return list;Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;TreeNode top = null;while (cur != null || !stack.isEmpty()) {while(cur != null) {stack.push(cur);list.add(cur.val);cur = cur.left;}top = stack.pop();cur = top.right;}return list;
}
- 二叉树的中序遍历
public List<Integer> inorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();if (root == null) return list;Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;TreeNode top = null;while (cur != null || !stack.isEmpty()) {while(cur != null) {stack.push(cur);cur = cur.left;}top = stack.pop();list.add(top.val);cur = top.right;}return list;
}
- 二叉树的后序遍历
public List<Integer> postorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();if (root == null) return list;Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;TreeNode top = null;while (cur != null || !stack.isEmpty()) {while(cur != null) {stack.push(cur);cur = cur.left;}top = stack.peek();cur = top.right;if(cur == null) {TreeNode tmp = stack.pop();list.add(tmp.val);while(!stack.isEmpty() && stack.peek().right == tmp) {tmp = stack.pop();list.add(tmp.val);}}}return list;
}
- 判断一棵树是不是完全二叉树
boolean isCompleteTree(TreeNode root) {if(root == null) {return true;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (true) {TreeNode top = queue.poll();if(top != null) {queue.offer(top.left);queue.offer(top.right);} else {break;}}while (!queue.isEmpty()) {if(queue.poll() != null) {return false;}}return true;
}
相关文章:

【Java刷题】二叉树
相同的树 public boolean isSameTree(TreeNode p, TreeNode q) {if(p null && q null) {return true;} else if(p ! null && q ! null) {if(p.val ! q.val) {return false;} else {return isSameTree(p.left, q.left) && isSameTree(p.right, q.rig…...
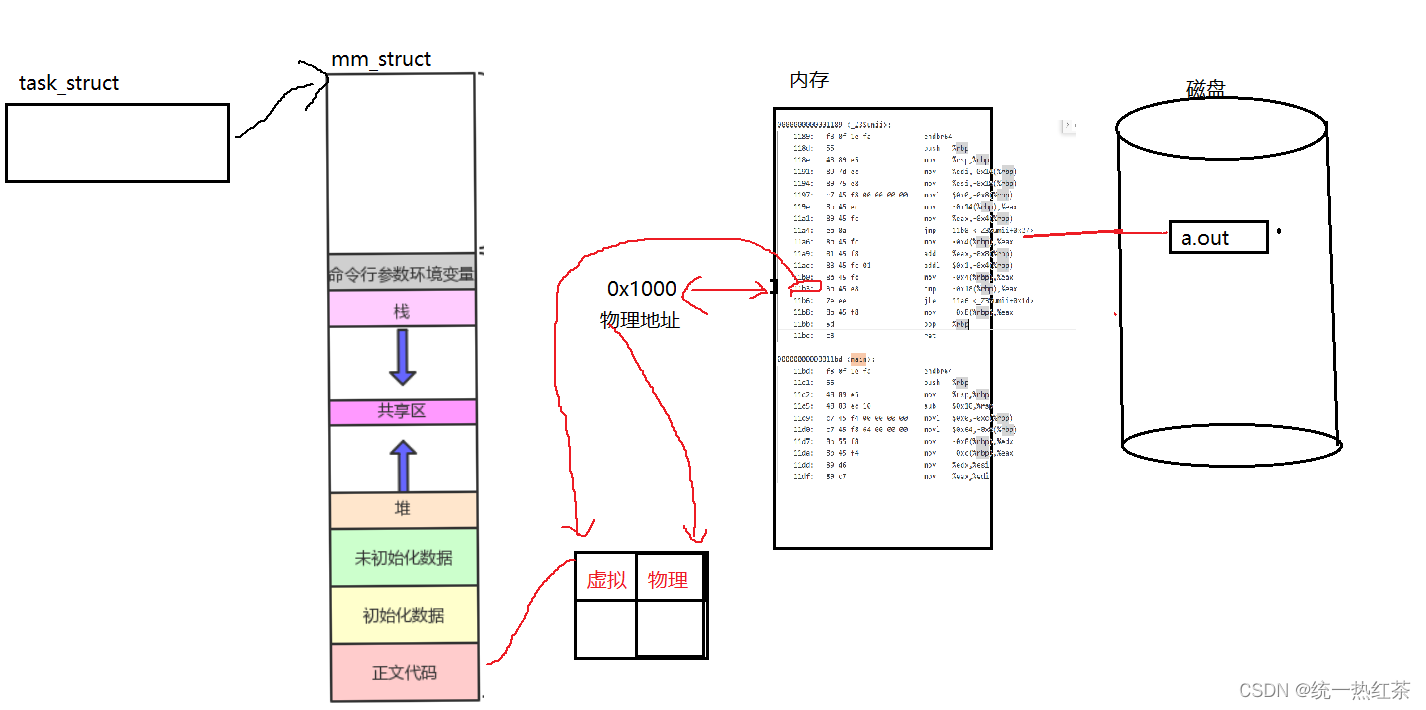
【Linux】程序地址空间之动态库的加载
我们先进行一个整体轮廓的了解,随后在深入理解细节。 在动态库加载之前还要说一下程序的加载,因为理解了程序的加载对动态库会有更深的理解。 轮廓: 首先,不管是程序还是动态库刚开始都是在磁盘中的,想要执行对应的可…...
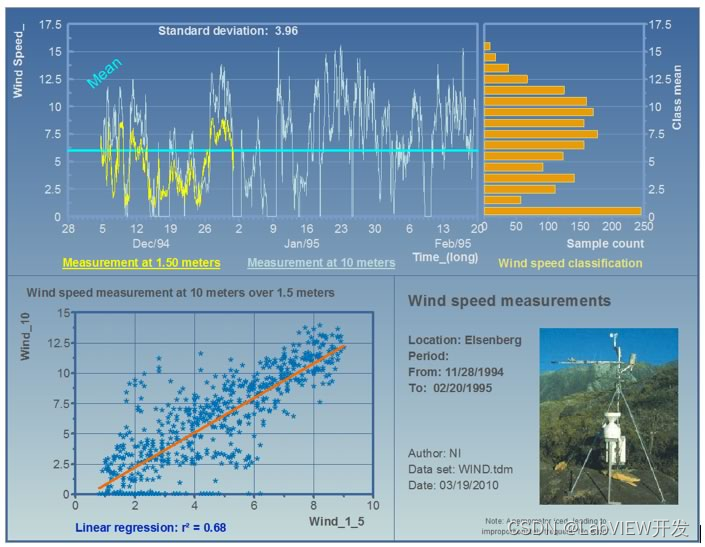
LabVIEW处理大量数据时,怎样确保数据的准确性和完整性?
在LabVIEW处理中,确保大量数据的准确性和完整性至关重要。以下是详细的多角度分析和建议,以确保在LabVIEW中处理大量数据时,数据的准确性和完整性: 1. 数据采集阶段 1.1 高精度硬件选择 选择高精度的数据采集硬件,如…...

容器是什么?
概念 容器可以被看作是一种轻量级的虚拟化技术。与传统虚拟化技术相比,容器不需要为每个应用程序提供单独的操作系统,它们共享宿主机的操作系统内核。这使得容器更加轻便和高效。 想象一下,容器就像是一艘艘可以在海洋中独立航行的货轮&…...

#15 从Stable Diffusion生成的艺术中寻找灵感
文章目录 前言1. Stable Diffusion简介2. 寻找灵感的途径2.1 深入探索主题2.2 结合多种艺术风格2.3 实验不同的创意组合 3. 灵感应用3.1 艺术创作3.2 设计项目3.3 故事讲述 4. 实践建议4.1 记录和迭代4.2 开放实验4.3 结合个人风格 结论 前言 在当今的数字时代,人工…...
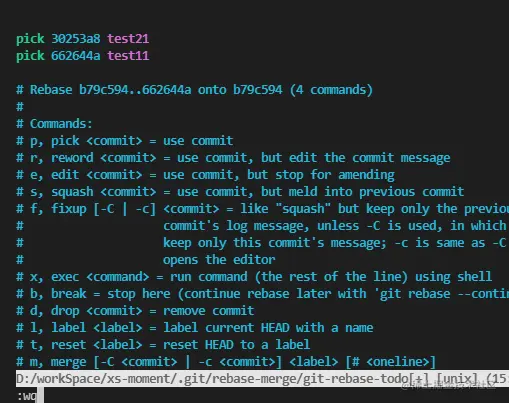
git rebase
1. git rebase的意义 首先理解这个rebase,它的意思是re base,翻译过来就是“重新基于”。 意义是:重新整理当前分支的开发线,使其变成基于某个开发节点的开发线。 2. rebase用于并行开发 构造两个分支master和feature…...
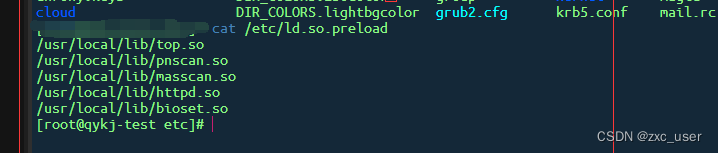
Docker引起的漏洞问题
前言 测试环境上的中间件和java应用都是由docker进行部署的,但是因为docker的镜像访问有时候需要外网,由此引发了问题,在docker文件中 /usr/lib/systemd/system/docker.service 原有的配置为,可以看到进行了加密 ExecStart/usr/bin/dockerd --tlsverify --tlscacert/etc/docker…...

Oracle基本数据类型
在Oracle数据库中,数据类型是描述数据存储格式的属性。不同的数据类型允许存储不同种类的数据。以下是Oracle中的一些基本数据类型: 1. 字符数据类型 - CHAR(size): 定长字符数据,最大长度为2000字节。 - VARCHAR2(size): 变长字符数据…...

VS+QT+OCC创建坐标界面
1、安装并配置好项目后,填写如下代码: #pragma once#include <Standard_Handle.hxx> #include <V3d_Viewer.hxx> #include <OpenGl_GraphicDriver.hxx> #include <WNT_Window.hxx> #include <V3d_View.hxx> #include <…...

VUE2.7项目配置webpack打包-详细操作步骤
一、Webpack简介 Webpack是一个打包工具,可以把JS、CSS、Node Module、Coffeescrip、SCSS/LESS、图片等都打包在一起,因此,现在几乎所有的SPA项目、JS项目都会用到Webpack。 官网:https://webpack.js.org GitHub为https://git…...
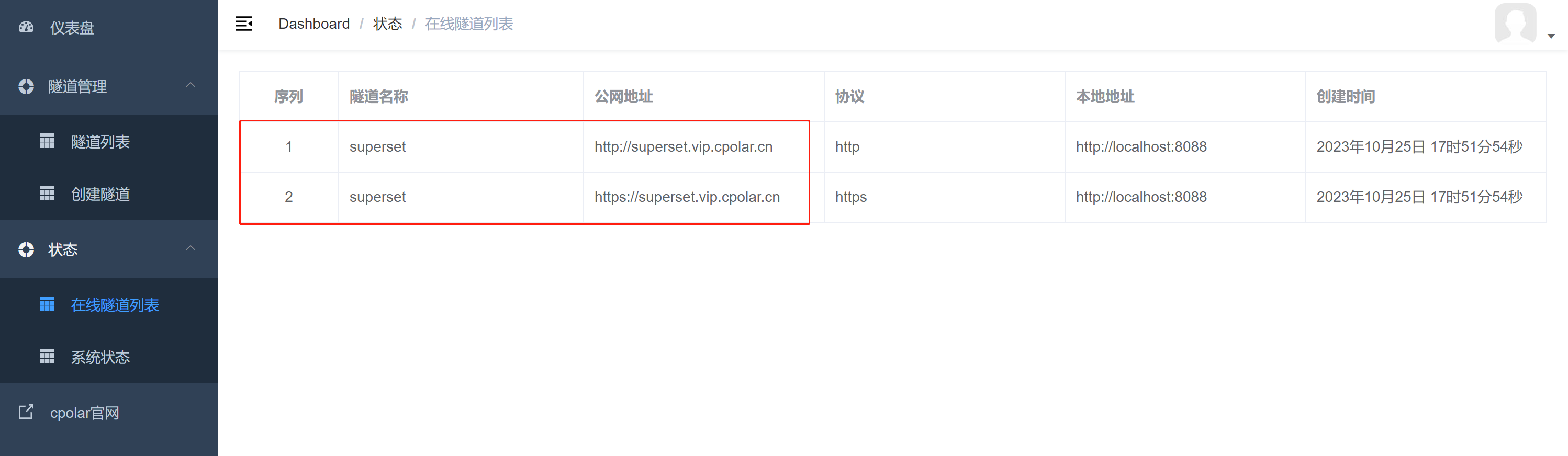
Linux系统Docker部署Apache Superset并实现远程访问详细流程
目录 前言 1. 使用Docker部署Apache Superset 1.1 第一步安装docker 、docker compose 1.2 克隆superset代码到本地并使用docker compose启动 2. 安装cpolar内网穿透,实现公网访问 3. 设置固定连接公网地址 前言 作者简介: 懒大王敲代码࿰…...
Cochrane Library循证医学数据库的介绍及文献下载
今天要讲的数据库是Cochrane Library循证医学数据库,我们先来了解一下该数据库: Cochrane Library是国际Cochrane Collaboration的主要产品,由英国Wiley InterScience公司出版发行。是一个提供高质量证据的数据库,是循证医学的证…...
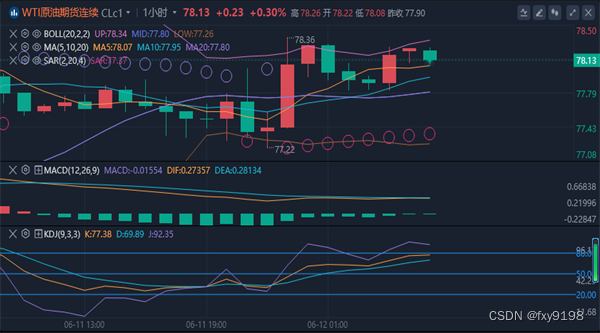
冯喜运:6.12今日黄金原油行情还会涨吗?黄金原油独家操作策略
【黄金消息面分析】:据荷兰国际集团(ING)大宗商品策略师埃瓦?曼西(Ewa Manthey)称,黄金价格正面临来自美元走强和中国需求疲软的新阻力,但一旦美联储开始降息,黄金价格将恢复反弹。 【黄金技术面分析】:黄金…...
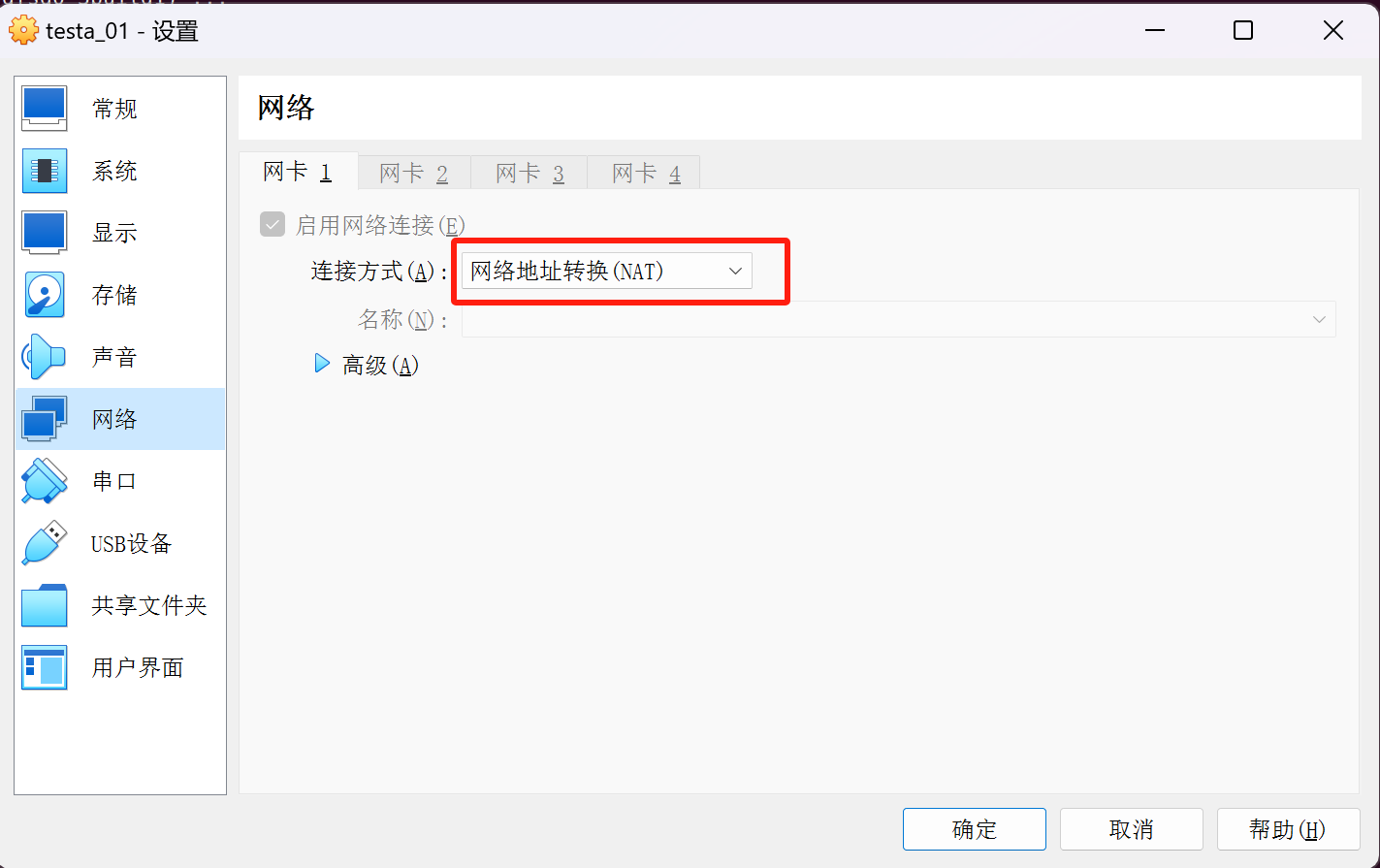
VM ubuntu终端使用Host代理的方法
1、设置网络地址转换NAT 2、在终端敲击如下命令 先敲击 ip route show 找到网关。再敲击如下命令: export http_proxyhttp://10.0.2.2:33210 export https_proxyhttp://10.0.2.2:33210 export HTTP_PROXYhttp://10.0.2.2:33210/ export HTTPS_PROXYhttp://10.0.2.…...
 - 三语言AC题解(Python/Java/Cpp))
【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 破译犯罪时间(100分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 📎在线评测链接 破译犯罪时间(100分) 🌍 评测功能需要订阅专栏后私信联系清…...
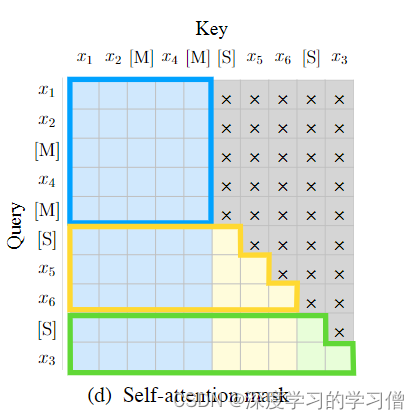
大模型学习之GLM结构
探索GLM:一种新型的通用语言模型预训练方法 随着人工智能技术的不断进步,自然语言处理(NLP)领域也迎来了革命性的发展。OpenAI的ChatGPT及其后续产品在全球范围内引起了广泛关注,展示了大型语言模型(LLM&a…...

C#类库打包支持多个版本的类库
修改csproj <Project Sdk"Microsoft.NET.Sdk"><PropertyGroup><TargetFrameworks>netcoreapp3.1;net5.0;net6.0;net7.0;net8.0</TargetFrameworks><PackageId>xxxx</PackageId><Version>1.0.0</Version><Author…...

一文介绍暗区突围手游 游戏特色、具体玩法和独特的玩法体验
🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 《暗区突围》是一款由腾讯魔方工作室群开发的第一人称射击游戏,于 2022 年 7 月 13 日正式公测,支持 Android 和 iOS 平台。这款游戏以从虚构的暗区收集物资并安全撤离作为最终目…...

Unity基础(三)3D场景搭建
目录 简介: 一.下载新手资源 二.创建基本地形 三.添加场景细节 四,添加水 五,其他 六. 总结 简介: 在 Unity 中进行 3D 场景搭建是创建富有立体感和真实感的虚拟环境的关键步骤。 首先,需要导入各种 3D 模型资源,如建筑物、角色、道具等。这些模…...

在Spring Boot中使用Sa-Token实现路径拦截和特定接口放行
在Spring Boot中使用Sa-Token实现路径拦截和特定接口放行 很喜欢的一段话:别想太多,好好生活,也许日子过着过着就会有答案,努力走着走着就会有温柔的着落。 春在路上,花在枝上,所有的美好都在路上ÿ…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...
