当前位置： 首页 > news >正文

vue问题记录

news 2026/2/9 3:05:41

vue3 路由跳转携带参数

路由跳转携带参数

query方法

//跳转传参
this.$router.push({path:'/home',query: {id:'1'}})
//接受参数
this.$route.query.id

问题：刷新页面，参数会丢失—未解决

将参数存在本地存储中，但是组件销毁时，清除本地存储

相关文章：

vue问题记录

vue3 路由跳转携带参数 路由跳转携带参数 query方法 //跳转传参 this.$router.push({path:/home,query: {id:1}}) //接受参数 this.$route.query.id问题：刷新页面，参数会丢失—未解决 将参数存在本地存储中，但是组件销毁时，清…...

编程日记 2024/6/12 10:31:30

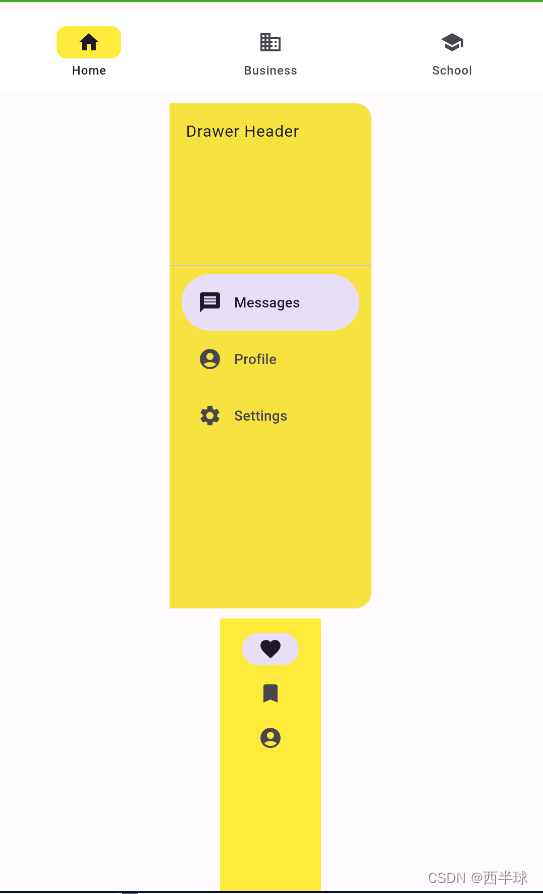
Flutter - Material3适配

demo 地址: https://github.com/iotjin/jh_flutter_demo 代码不定时更新，请前往github查看最新代码 Flutter - Material3适配 对比图具体实现一些组件的变化 代码实现Material2的ThemeDataMaterial3的ThemeData Material3适配官方文档 flutter SDK升级到3.16.0之后 …...

编程日记 2024/6/12 10:30:27

一个有趣的c++案例

1. 源码 #include <stdio.h> #include <stdint.h> #include <iostream>using namespace std;uint8_t a 0; uint8_t b 0;#define MY_LOG#ifdef MY_LOG#define my_log(...) printf(__VA_ARGS__); fflush(stdout)#else #define my_log(...) #endifvoid …...

编程日记 2024/6/12 10:28:25

【python】OpenCV—Background Estimation（15）

文章目录 中值滤波中值滤波得到图像背景移动侦测 学习来自 OpenCV基础&#xff08;14&#xff09;OpenCV在视频中的简单背景估计 中值滤波 中值滤波是一种非线性平滑技术&#xff0c;主要用于数字信号处理&#xff0c;特别是在图像处理中去除噪声。 一、定义与原理 定义&am…...

编程日记 2024/6/12 10:24:20

【Java毕业设计】基于JavaWeb的旅游论坛管理系统

文章目录 摘 要目 录1 概述1.1 研究背景及意义1.2 国内外研究现状1.3 拟研究内容1.4 系统开发技术1.4.1 Java编程语言1.4.2 vue技术1.4.3 MySQL数据库1.4.4 B/S结构1.4.5 Spring Boot框架 2 系统需求分析2.1 可行性分析2.2 系统流程2.2.1 操作流程2.2.2 登录流程2.2.3 删除信息…...

编程日记 2024/6/12 10:22:18

讲一下v-model的底层实现原理?

什么是v-model&#xff1f; 在Vue.js中&#xff0c;v-model是一个用于实现双向数据绑定的指令。它通常用于表单控件上&#xff0c;以便能够在视图和数据模型之间自动同步数据。具体来说&#xff0c;当用户在输入框中输入内容时&#xff0c;数据模型会自动更新&#xff1b;当数…...

编程日记 2024/6/12 10:21:17

大模型基础——从零实现一个Transformer(3)

大模型基础——从零实现一个Transformer(1)-CSDN博客 一、前言 之前两篇文章已经讲了Transformer的Embedding,Tokenizer,Attention,Position Encoding, 本文我们继续了解Transformer中剩下的其他组件. 二、归一化 2.1 Layer Normalization layerNorm是针对序列数据提出的一种…...

编程日记 2024/6/12 10:20:16

一二三应用开发平台应用开发示例——概述、应用开发示例简介及创建前后端模块

概述 对于应用开发平台的核心基石——系统管理模块&#xff0c;我精心撰写了一份详尽的说明手册。该手册旨在从使用者的角度出发&#xff0c;不仅全面阐述系统的各项属性和功能&#xff0c;更着重强调使用过程中的注意事项和最佳实践。 在手册的编写过程中&#xff0c;我特别…...

编程日记 2024/6/12 10:19:15

springboot+minio+kkfileview实现文件的在线预览

在原来的文章中已经讲述过springbootminio的开发过程&#xff0c;这里不做讲述。 原文章地址&#xff1a; https://blog.csdn.net/qq_39990869/article/details/131598884?spm1001.2014.3001.5501 如果你的项目只是需要在线预览图片或者视频那么可以使用minio自己的预览地址进…...

编程日记 2024/6/12 10:17:07

HTML5+CSS3小实例：粘性文字的滚动效果

实例：粘性文字的滚动效果 技术栈：HTML+CSS 效果： 源码： 【HTML】 <!DOCTYPE html> <html lang="zh-CN"><head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-sca…...

编程日记 2024/6/12 10:16:06

Java 关于抽象 -- Java 语言的抽象类、接口和函数式接口

大家好，我是栗筝i，这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 008 篇文章，在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验，并希望进一步完善自己对整个 Java 技术体系来充实自…...

编程日记 2024/6/12 10:15:04

用 Notepad++ 写 Java 程序

安装包 百度网盘 提取码&#xff1a;6666 安装步骤 双击安装包开始安装。 安装完成&#xff1a; 配置编码 用 NotePad 写 Java 程序时&#xff0c;需要设置编码。 在 设置&#xff0c;首选项&#xff0c;新建 中进行设置&#xff0c;可以对每一个新建的文件起作用。 Note…...

编程日记 2024/6/12 10:13:01

malloc brk mmap

malloc 是一个库函数&#xff0c;通常在 C 标准库中实现&#xff0c;用于动态内存分配。malloc 的具体实现可能因库、操作系统和平台而异&#xff0c;但通常它会与底层操作系统提供的内存管理功能进行交互。 对于大多数现代操作系统&#xff08;如 Unix、Linux、Windows 等&am…...

编程日记 2024/6/12 10:12:00

java多线程相关概念

在Java多线程编程中&#xff0c;有几个关键的术语需要理解&#xff1a; 1.线程(Thread)&#xff1a;线程是操作系统能够进行运算调度的最小单位&#xff0c;它被包含在进程之中&#xff0c;是进程中的实际运作单位。 2.进程(Process)&#xff1a;进程是系统进行资源分配和调度…...

编程日记 2024/6/12 10:10:59

【html】简单网页模板源码

大家每一次在写网页的时候会不会因为布局而困扰今天就给大家带来一个我自己亲自编写的网页的基本的模板大家可以直接去利用&#xff0c;大家也可以利用自己的想法去做空间的美化和完善。 源码&#xff1a; html: <!DOCTYPE html> <html lang"zh"><…...

编程日记 2024/6/12 10:08:57

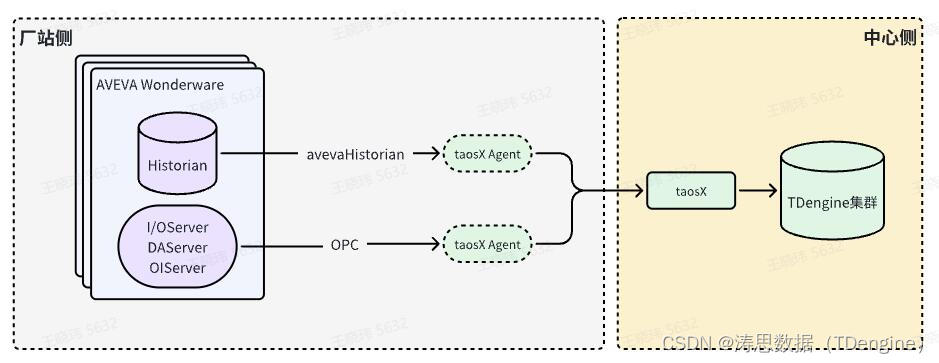
借助Historian Connector + TDengine，打造工业创新底座

在工业自动化的领域中&#xff0c;数据的采集、存储和分析是实现高效决策和操作的基石。AVEVA Historian (原 Wonderware Historian) 作为领先的工业实时数据库&#xff0c;专注于收集和存储高保真度的历史工艺数据。与此同时&#xff0c;TDengine 作为一款专为时序数据打造的高…...

编程日记 2024/6/12 10:07:56

51单片机-实机演示（LED点阵）

目录 前言: 一.线位置 二.扩展 三.总结 前言: 这是一篇关于51单片机实机LED点阵的插线图和代码说明.另外还有一篇我写的仿真的连接在这:http://t.csdnimg.cn/ZNLCl,欢迎大家的点赞,评论,关注. 一.线位置 接线实机图. 引脚位置注意: 1. *-* P00->RE8 P01->RE7 …...

编程日记 2024/6/12 10:06:54

STM32硬件接口I2C应用（基于MP6050）

目录 概述 1 STM32Cube控制配置I2C 1.1 I2C参数配置 1.2 使用STM32Cube产生工程 2 HAL库函数介绍 2.1 初始化函数 2.2 写数据函数 2.3 读数据函数 3 认识MP6050 3.1 MP6050功能介绍 3.2 加速计测量寄存器 ​编辑3.3 温度计量寄存器 3.4 陀螺仪测量寄存器 4 MP60…...

编程日记 2024/6/12 10:04:52

基于JSP的贝儿米幼儿教育管理系统

开头语&#xff1a; 你好呀&#xff0c;我是计算机学长猫哥&#xff01;如果您对本系统感兴趣或者有相关需求&#xff0c;文末可以找到我的联系方式。 开发语言&#xff1a; Java 数据库&#xff1a; MySQL 技术&#xff1a; JSP技术 工具&#xff1a; IDEA/Eclipse、…...

编程日记 2024/6/12 10:02:50

数字化与文化交融，树莓集团助力园区文化升级

树莓集团在产业园运营领域建设了特色空间布局&#xff0c;包括产业实训基地、产业办公中心、业务资源平台、产学研中心、数字资产空间、双创孵化空间、产业实验室和人才项目转化中心等八大板块&#xff0c;共同构建了一个全面而深入的产业支撑体系&#xff0c;为园区文化建设提…...

编程日记 2024/6/12 10:01:49

铭豹扩展坞 USB转网口 突然无法识别解决方法

当 USB 转网口扩展坞在一台笔记本上无法识别，但在其他电脑上正常工作时，问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤，帮助你快速找到故障原因： 背景： 一个M-pard（铭豹）扩展坞的网卡突然无法识别了，扩展出来的三个USB接口正常。…...

编程新知 2026/2/8 4:37:22

树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频

使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源&#xff1a; http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

编程新知 2025/11/5 13:03:58

8k长序列建模，蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂

蛋白质结合剂&#xff08;如抗体、抑制肽&#xff09;在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上&#xff0c;高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术&#xff0c;但这类方法普遍面临资源消耗巨大、研发周期冗长…...

编程新知 2026/1/25 13:18:12

为什么需要建设工程项目管理？工程项目管理有哪些亮点功能？

在建筑行业&#xff0c;项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升&#xff0c;传统的管理模式已经难以满足现代工程的需求。过去&#xff0c;许多企业依赖手工记录、口头沟通和分散的信息管理&#xff0c;导致效率低下、成本失控、风险频发。例如&#…...

编程新知 2026/2/4 12:35:34

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法（ISWC2024）

笔记整理&#xff1a;刘治强&#xff0c;浙江大学硕士生&#xff0c;研究方向为知识图谱表示学习&#xff0c;大语言模型 论文链接&#xff1a;http://arxiv.org/abs/2407.16127 发表会议&#xff1a;ISWC 2024 1. 动机 传统的知识图谱补全&#xff08;KGC&#xff09;模型通过…...

编程新知 2026/1/31 12:03:23

Java 加密常用的各种算法及其选择

在数字化时代&#xff0c;数据安全至关重要&#xff0c;Java 作为广泛应用的编程语言&#xff0c;提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景&#xff0c;有助于开发者在不同的业务需求中做出正确的选择。​ 一、对称加密算法…...

编程新知 2025/11/22 20:41:02

在WSL2的Ubuntu镜像中安装Docker

Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包&#xff1a; for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

编程新知 2026/2/4 16:23:56

纯 Java 项目（非 SpringBoot）集成 Mybatis-Plus 和 Mybatis-Plus-Join

纯 Java 项目&#xff08;非 SpringBoot&#xff09;集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

编程新知 2025/9/26 12:26:35

Razor编程中@Html的方法使用大全

文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

编程新知 2026/1/28 4:50:33

链式法则中 复合函数的推导路径 多变量“信息传递路径”

非常好&#xff0c;我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题&#xff0c;统一使用 二重复合函数&#xff1a; z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y))​ 来全面说明。我们会展示其全微分形式&#xff08;偏导…...

编程新知 2026/2/8 12:07:50