【数据结构】查找(顺序查找、二分查找、索引顺序查找、二叉排序树、平衡排序树、B树、B+树、哈希表)
目录
- 数据结构——查找
- 何为查找
- 1. 查找表
- 2. 关键字
- 3. 查找方法效果评价指标——平均查找长度ASL(Average Search Length)
- 静态查找表
- 1.顺序查找
- 2.二分查找
- 二分查找判定树
- 3.静态查找表—索引顺序表的查找
- 索引顺序查找表的算法原理:
- 动态查找树表
- 1. 二叉排序树
- 2. 二叉树的检索算法
- 3. 二叉排序树的插入算法
- 4. 二叉排序树的删除算法
- 5. 最佳二叉排序树
- 2.平衡二叉树
- 平衡二叉树(AVL树)(平衡二叉排序树)
- 平衡旋转技术
- B-树 和B+树
- 哈希表查找
- 哈希表"冲突"现象——冲突处理
- 1. 开放定址法
- 2. 再哈希表法
- 3. 链地址法
- 4. 建立一个公共溢出区
- 哈希表的查找
- 哈希表的删除操作
数据结构——查找
何为查找
1. 查找表
-
查找表由同一类型的数据元素(或记录)构成的集合 -
查找表的操作包括:
- 查询某个特定的数据元素是否在查找表中;
- 检索某个特定的数据元素的各种属性;
- 在查找表中插入一个数据元素;
- 从查找表中删去某个数据元素。
- 查找表的分类:
- 静态查找表:只允许做查询和检索操作的查找表。
- 动态查找表:除查询和检索操作外,还允许进行插入和删除操作的查找表。
2. 关键字
关键字:是**数据元素(或记录)**中某个数据项的值,用以标识(识别)一个数据元素(或记录)
若此关键字可以识别唯一的一个记录,则称之谓**“主关键字”**
若此关键字能识别若干记录,则称之谓**“次关键字”**
查找表的查询和检索通常是根据关键字进行的
根据给定的值,在查找表中确定一个其关键字等于给定值的数据元素或记录
- 若查找表中存在这样一个记录(数据元素),则称查找成功。查找结果给出整个记录(数据元素)的信息,或指示该记录(数据元素)在查找表中的位置;
- 否则称此查找不成功。查找结果给出“空记录 ”或“空指针”
3. 查找方法效果评价指标——平均查找长度ASL(Average Search Length)
查找速度:平均查找长度ASL(Average Search Length)-为确定记录在表中的位置,需要与给定值进行比较的次数的期望值叫查找算法的平均查找长度
静态查找表–顺序查找性能分析:
查找成功的平均查找长度(查找成功的情况下,平均找一个数据元素需要的比较次数称为查找成功的平均查找(检索)长度):
A S L = ( 1 + 2 + … + n ) / n = ( n + 1 ) / 2 ASL=(1+2+…+n)/n=(n+1)/2 ASL=(1+2+…+n)/n=(n+1)/2
说明:假设每个数据元素查找的概率相同
查找一次的平均检索长度(成功,失败)(*)
A S L = ( n + 1 ) / 2 + ( 1 + 2 + … + n ) / ( 2 ∗ n ) = 3 ( n + 1 ) / 4 ASL=(n+1)/2+(1+2+…+n)/(2*n)=3(n+1)/4 ASL=(n+1)/2+(1+2+…+n)/(2∗n)=3(n+1)/4
说明:假设每个数据元素查找的概率相同,并且查找一次成功和失败的概率也相同
静态查找表
1.顺序查找
查找方法:从表的一端顺序找到表的另一端 (以线性表表示静态查找表)
- 存储结构
无特殊要求(数组或链表都可以的)- 元素
顺序无要求(有序、无序都可以的 )
//顺序表定义
#define max 100
typedef struct{KeyType key; ;//说明:KeyType代表关键字的类型//……;
}ElemType typedef struct{ ElemType elem[max]; int length;
}SqList;
SqList L;顺序查找:
int search(SqList L, KeyTypex){ //KeyType代表关键字的类型for(int i=0;i<L.length;i++)if(L.elem[i].key==x) return i+1;//找到数据的位置 +1为了方便表示第几个数据return 0;
}
//说明:返回0说明没找到;若找到,返回是x线性表的第几个数据元素
为提高查找速度,设置哨兵项;查找表组织成线性表,线性表的数据元素从下标为1的数组元素开始存放;下标为0的数组元素作为哨兵项(说明:哨兵可设在低端,也可以设在高端)
查找x,首先将x放在下标为0的数组元素(哨兵),从表尾开始比较。若在哨兵
处相等,说明没找到,否则找到
int srearch(SqList L,KeyTypex)//KeyType代表关键字的类型
{ int k=L.length;L.elem[0].key=x;while(x!=L.elem[k].key)k--;return k;
}//L.elem[0]哨兵项
//说明:返回0说明没找到;若找到,返回是x线性表的第几个数据元素
//说明2:哨兵也可以设在线性表的表尾
静态查找表–顺序查找性能分析:
查找成功的平均查找长度(查找成功的情况下,平均找一个数据元素需要的比较次数称为查找成功的平均查找(检索)长度):
A S L = ( 1 + 2 + … + n ) / n = ( n + 1 ) / 2 ASL=(1+2+…+n)/n=(n+1)/2 ASL=(1+2+…+n)/n=(n+1)/2
说明:假设每个数据元素查找的概率相同
查找一次的平均检索长度(成功,失败)(*)
A S L = ( n + 1 ) / 2 + ( 1 + 2 + … + n ) / ( 2 ∗ n ) = 3 ( n + 1 ) / 4 ASL=(n+1)/2+(1+2+…+n)/(2*n)=3(n+1)/4 ASL=(n+1)/2+(1+2+…+n)/(2∗n)=3(n+1)/4
说明:假设每个数据元素查找的概率相同,并且查找一次成功和失败的概率也相同
2.二分查找
采用二分查找的要求:查找表组织成有序线性表(递增或递减),且采用顺序存储结构
特点:通过一次比较,将查找范围缩小一半
二分查找通用模板:
// 在单调递增序列a中查找>=x的数中最小的一个(即x或x的后继)
while (low < high)
{int mid = (low + high) / 2;if (a[mid] >= x)high = mid;elselow = mid + 1;
}// 在单调递增序列a中查找<=x的数中最大的一个(即x或x的前驱)
while (low < high)
{int mid = (low + high + 1) / 2;if (a[mid] <= x)low = mid;elsehigh = mid - 1;
}二分查找算法原理:
//有序(递增或递减),顺序存储结构
int binaryS(SqList L, KeyType x){int low=0, high=L.length-1, m;while(low<=high){m=(low+high)/2;//if(L.elem[m].key==x) return m+1; //若找到,返回是x线性表的第几个数据元素if(L.elem[m].key>x) high=m-1; else low=m+1;} return 0;
}
//说明:返回0说明没找到;若找到,返回是x线性表的第几个数据元素■ 二分查找的效率高,但是要将表按关键字排序。而排序本身是一种很费时的运算。既使采用高效率的排序方法也要花费 O ( n l o g n ) O(nlogn) O(nlogn)的时间。
■ 二分查找只适用顺序存储结构。为保持表的有序性,在顺序结构里插入和删除都必须移动大量的数据元素。因此,二分查找特别适用于那种一经建立就很少改动、而又经常需要查找的线性表。
■ 对那些查找少而又经常需要改动的线性表,可采用链表作存储结构,进行顺序查找。链表上无法实现二分查找。(*)
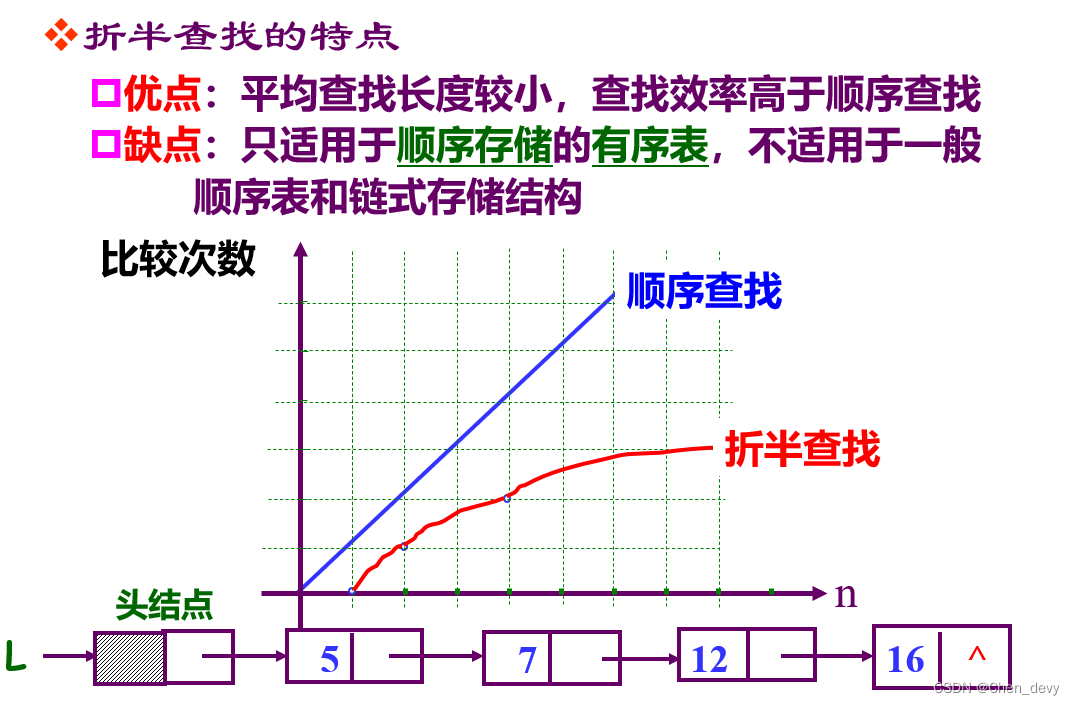

二分查找判定树


3.静态查找表—索引顺序表的查找
线性表分成若干块,每一块中的键值存储顺序是任意的,块与块之间****按键值排序,即后一块中的所有记录的关键字的值均大于前一块中最大键值。
建立一个索引表,该表中的每一项对应于线性表中的一块,每一项由键域(存放相应块的最大键值)和链域(存放指向本块地一个结点的指针)组成。
适用条件:分块有序表
索引顺序表的查找:
■ 首先对索引表采用二分查找或顺序查找方法查找,以确定待查记录所在的块。 ■
在线性表查找k,若其在线性表中存在,且位于第i块,那么一定有:第i-1块的 最大键值 < k ≤ 第 i 块的最大键值 最大键值<k≤第i块的最大键值 最大键值<k≤第i块的最大键值。 ■
然后在相应的块中进行顺序查找。
数据结构(结构体):
typedef struct{ KeyType key; //关键字域//…… ; // 其它域
}ElemType;//数据结构typedef struct{ ElemType *elem; // 数据元素存储空间基址int length; // 表的长度
}SSTable;//顺序表typedef struct{ KeyType MaxKey; //本块最大关键字int FirstLink; //本块第一个结点下标
}IndexTable;//索引表的类型索引顺序查找表的算法原理:
int Seach_Index(SSTable ST,IndexTable IT[],int b,int n,KeyType k){ int i=1,j;//b 为块儿数 Maxkey为每块儿中的最大值//索引表查找while((k>IT[i].MaxKey)&&(i<=b)) i++;if(i>b){ printf("\nNot found"); return(0); }j=IT[i].FirstLink; //块儿内查找while((k!=ST.elem[j].key)&&(ST.elem[j].key<=IT[i].MaxKey) &&(j<n))j++; //输出查找结果 if(k!=ST.elem[j].key){j=0; printf("\nNot found"); }return(j);
}■ 表长为n的线性表,整个表分为b块,前 b-1块中的记录数为s=⎡n/b⎤,第b块中的记录数小于或等于s。
■ A S L = ( b + 1 ) / 2 + ( s + 1 ) / 2 ASL=(b+1)/2+(s+1)/2 ASL=(b+1)/2+(s+1)/2
(*)
■ 当 s = 根号n ,ASL最小 根号n +1
①索引表查找可使用何方法?①顺序、折半查找
②块内查找可使用何方法? ②只能使用顺序查找
③数据可否用链式存储? ③可以使用链式存储
对那些查找少而又经常需要改动的线性表,可采用链表作存储结构,进行顺序查找。链表上无法实现二分查找。(*)
动态查找树表
1. 二叉排序树
- 二叉排序树定义:
二叉排序树或者是一棵空树;或者是具有如下特性的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于根结点的值;
- 它的左、右子树也都分别是二叉排序树 (递归)
-
二叉排序树的中序遍历结果递增有序
判断一棵二叉树是否为二叉排序树:看其中序遍历结果是否递增有序
因此,一个无序序列,可通过构建一棵二叉排序树而成为有序序列。 -
二叉排序树的主要作用与操作
■ 二叉排序树主要作用:检索,排序
■二叉排序树主要操作:检索,插入(建立),删除
检索:
■ 在二叉排序树中查找是否存在值为x的结点。
■ 查找过程为:
① 若二叉排序树为空,查找失败。
②否则,将x与二叉排序树的根结点关键字值比较:若相等,查找成功,结束;
否则,
a.若x小于根结点关键字,在左子树上继续进行,转①
b.若x大于根结点关键字,在右子树上继续进行,转①
- 二叉排序树的存储结构**(二叉链表)**
//二叉链表作为二叉排序树的存储结构
typedef struct NODE{int key;//数据元素的关键字//… ;//数据元素的其他数据项 struct NODE *lc,*rc;
}BiNode,*BiTree;2. 二叉树的检索算法
//二叉排序树的检索算法
Bitree Search(BiNode *t, int x){ BiTree p; //p=t;while(p!=NULL){ //没找到就是返回空指针if (x==p->key) //找到就返回return p; if (x < p->key) //左右搜索p=p->lc;else p=p->rc;
}
return p;
}//函数返回查找结果,没找到为空指针!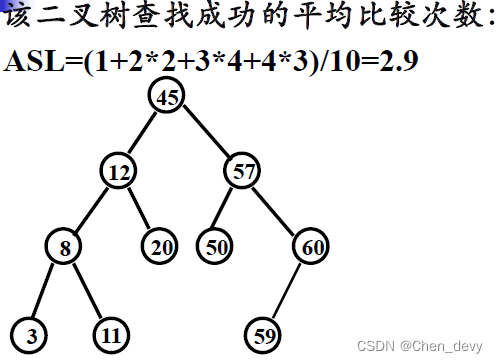
3. 二叉排序树的插入算法
向二叉排序树中插入x:
先要在二叉排序树中进行查找,若查找成功, 按二叉排序树定义,待插入数据已存在,不用插入;查找不成功时,则插入之。
新插入结点一定是作为叶子结点添加上去的。(*)
建立一棵二叉排序树则是逐个插入结点的过程。(*)
同一组数据,输入顺序不同,所建二叉排序树不同!
//int Insert(Bitree &t,int x)//二叉排序树的插入算法
{ BiTree q, p, s;q=NULL; p=t; ;//p为正在查看的节点,初始从根节点开始;q为p的双亲节点,根节点无双亲节点 while(p!=NULL){ //查找if (x==p->key) return 0;//在当前的二叉排序树中找到x,直接返回,不再做插入 q=p;//记录上一个位置if (x<p->key) p=p->lc; else p=p->rc;}//最后没找到的话 就是插入到 q的左孩子或右孩子处s=(BiTree)malloc(sizeof(Binode)) ;//没找到x,做插入:先申请节点空间 s->key=x; //初始化s->lc=NULL; s->rc=NULL ;//存放x,设为叶节点if(q==NULL)t=s;//若原先的二叉树是一棵空树,新插入的x对应的节点s为插入后二叉树的根节点//这个很重要 要不然空树 后面插入 就报错了。。。 else if(x<q->key) q->lc=s; ;//插入s为q的孩子else q->rc=s; return 1;
}
4. 二叉排序树的删除算法
从二叉排序树中删除一个结点之后,使其仍能保持二叉排序树的特性。
- 被删结点为叶结点,由于删去叶结点后不影响整棵树的特性,所以只需将被删结点的双亲结点相应指针域改为空指针。
- 若被删结点只有右子树
pr或只有左子树pl,此时,只需将pr或pl替换被删结点即可。 - 若被删结点既有左子树
pl又有右子树pr,可按中序遍历保持有序进行调整。
左右孩子均存在
用左子树中最大的结点q的值替换被删结点,再删"q" 或 用右子树中最小的结点w的值替换被删结点,再删"w"
结点q (和w)的特点是最多只有一个孩子
左子树中最大结点的特点是 左子树的根节点一直向右下 直到p->rchild==NULL为真,此时p就是那个左子树中的最大结点。
右子树中最小结点的特点是右子树的根节点一直向左下,直到p->lchild==NULL为真,此时p就是那个右子树中的最小结点。
5. 最佳二叉排序树
二叉排序树查找过程与二分查找判定树相似
-
n个数据元素按照不同的输入顺序构造的二叉排序树不同,其中平均查找性能最高的为最佳二叉排序树.
-
按照二分查找判定树的建立过程建立的二叉排序树为最佳二叉排序树。
-
二叉排序树的查找速度一般比顺序查找快,但如果是单枝树则一样快。
注意单枝树的情况
2.平衡二叉树
平衡二叉树(AVL树)(平衡二叉排序树)
希望所建的二叉排序树均为平衡二叉树 (AVL树)
注意需要时刻考虑到 空树 以及 单枝树 的情况
平衡二叉树:空树,或者是具有下列性质的二叉树:
- 左、右子树都是平衡二叉树 (递归)
- 左、右子树高度之差的绝对值不超过1
- 树中每个结点的左、右子树高度之差的绝对值不大于1。
结点的平衡因子 B F = 结点的左子树深度 − 右子树深度 结点的平衡因子BF=结点的左子树深度-右子树深度 结点的平衡因子BF=结点的左子树深度−右子树深度
平衡二叉树每个结点的平衡因子的绝对值不超过1
平衡旋转技术
如果在一棵AVL树中插入一个新结点,就有可能造成失衡,此时必须重新调整树的结构,使之恢复平衡。我们称调整平衡过程为平衡旋转。
平衡旋转可以归纳为四类:
- LL平衡旋转–单向右旋
- RR平衡旋转–单向左旋
- LR平衡旋转–先左旋后右旋
- RL平衡旋转–先右旋后左旋
旋转操作特点
- 对不平衡的最小子树操作
- 旋转后子树根节点平衡因子为0
- 旋转后子树深度不变故不影响全树,也不影响插入路径上所有祖先结点的平衡度
平衡树查找的时间复杂度为O(logn)
LL型—单向右旋
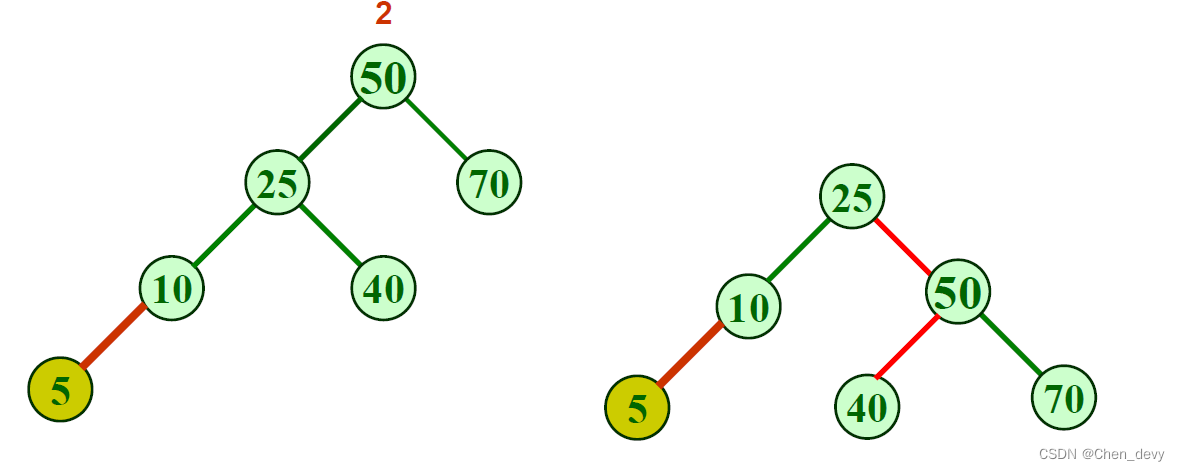
RR型—单向左旋

LR型—先左旋后右旋:
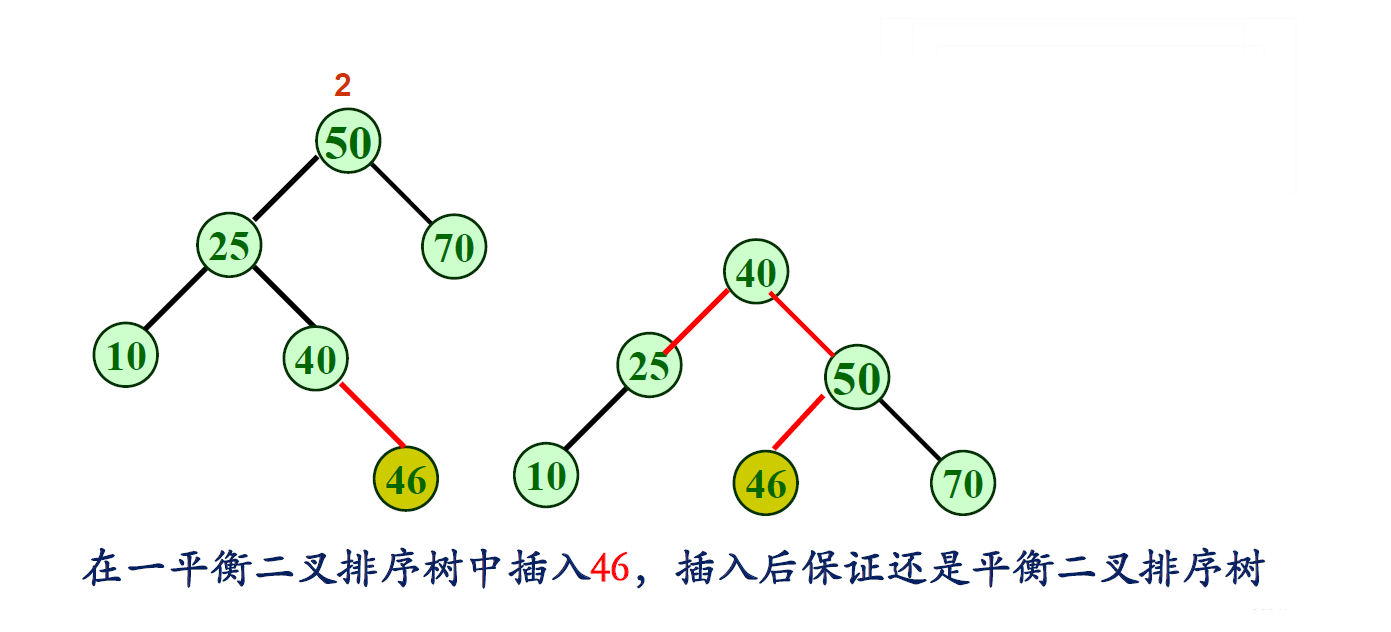 RL型—先右旋后左旋
RL型—先右旋后左旋
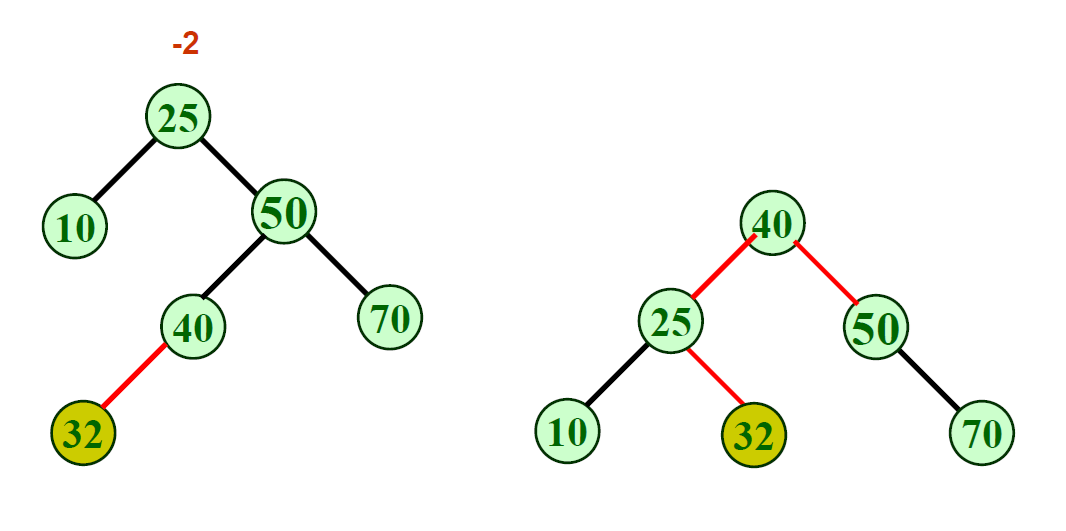
在平衡树上进行查找的过程和二叉排序树相同,因此,查找过程中和给定值进行比较的关键字的个数不超过平衡二叉树的深度。
(*)

B-树 和B+树
动态查找表,允许:查找,插入和删除操作
B-树是一种平衡的多路查找树。
哈希表查找
不同的表示方法,其差别仅在于:关键字和给定值进行比较的顺序不同
哈希函数是一个映象,即:将关键字的集合映射到某个地址集合上,它的设置很灵活,只要这个地址集合的大小不超出允许范围即可
哈希表构造方法:
哈希表"冲突"现象——冲突处理
实际应用中不保证总能找到一个不产生冲突的哈希函数。一般情况下,只能选择恰当的哈希函数,使冲突尽可能少地产生。
冲突处理方法:
- 开放定址法
- 再哈希表法
- 链地址法
- 建立一个公共溢出区
1. 开放定址法
d i d_i di称为增量,有三种取法:
- 线性探测再散列: d i = i d_i = i di=i
- 平方(二次)探测再散列: d i = 1 2 , − 1 2 , 2 2 , − 2 2 , 3 2 , − 3 2 , … d_i = 1^2 ,-1^2, 2^2, -2^2, 3^2, -3^2 , … di=12,−12,22,−22,32,−32,…
- 随机探测再散列: d i d_i di 是一组伪随机数列


增量 d i d_i di 应具有“完备性”(*)

2. 再哈希表法
3. 链地址法
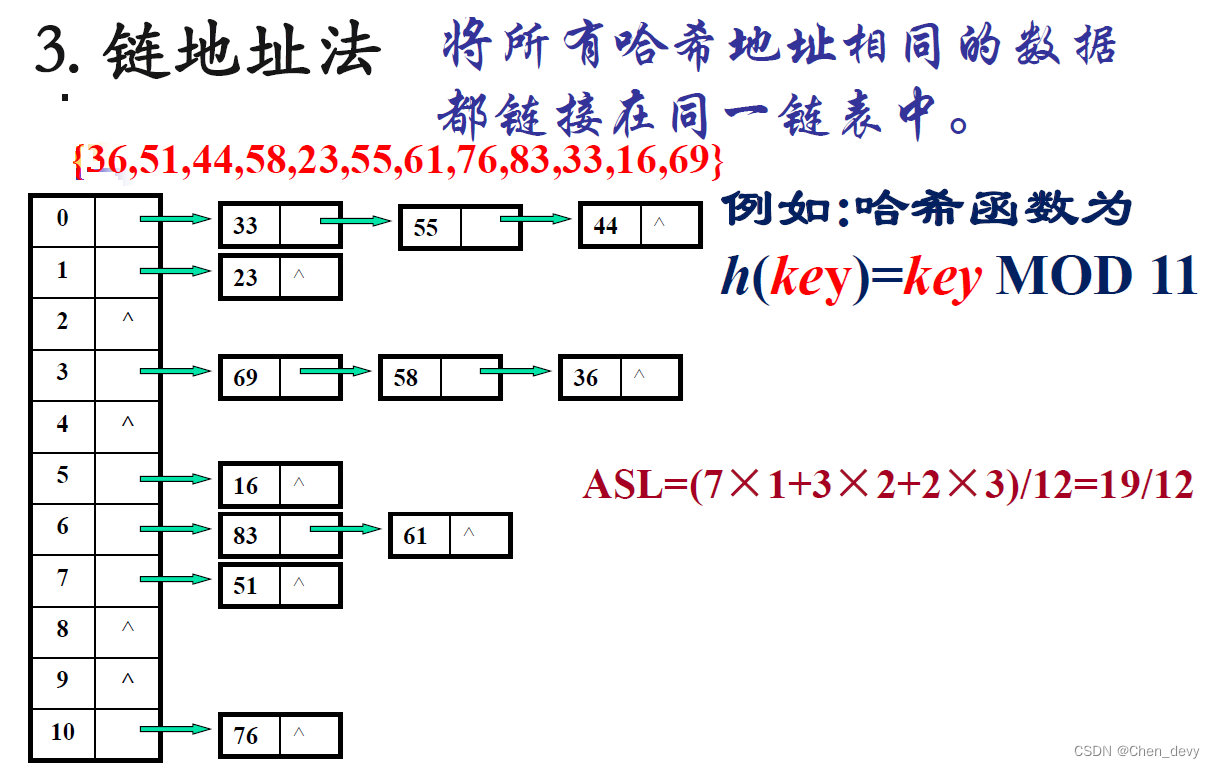
4. 建立一个公共溢出区
将发生冲突的数据元素顺序存放于一个公共的溢出区
哈希表的查找
查找过程和造表过程一致
哈希表饱和的程度,装载因子 α = n / m α=n/m α=n/m 值的大小(n—数据数,m—表的长度)

哈希表的删除操作
开放定址法:删除一个数据,为保证查找工作的正常进行不能真删----加删除标志
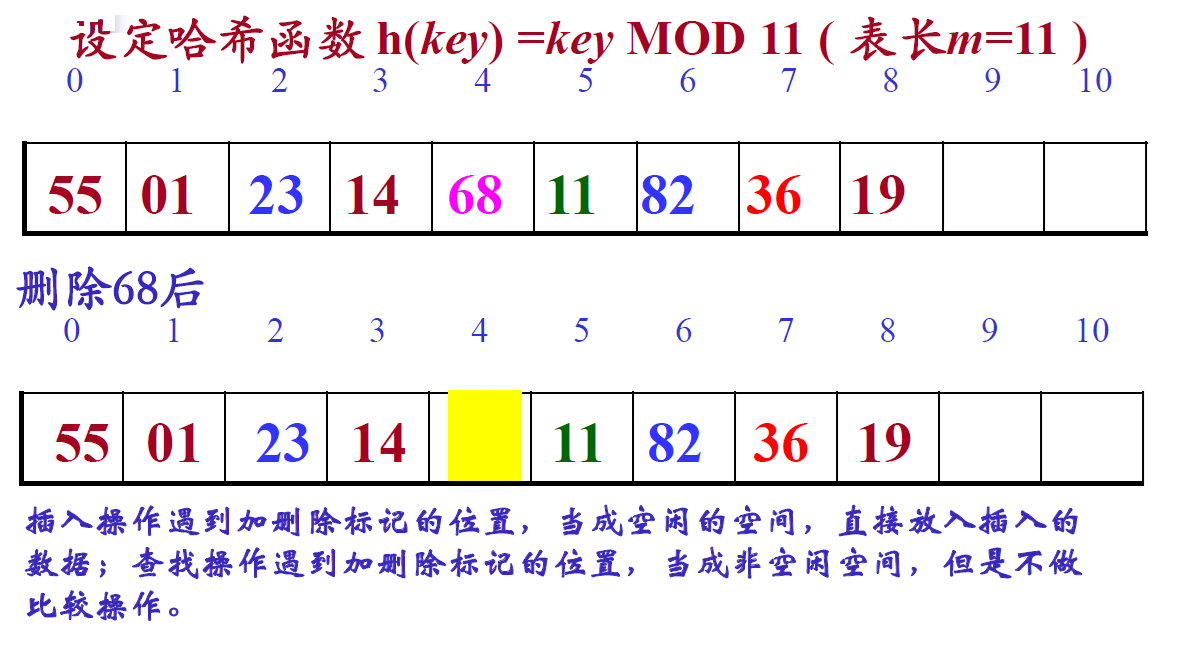
相关文章:

【数据结构】查找(顺序查找、二分查找、索引顺序查找、二叉排序树、平衡排序树、B树、B+树、哈希表)
目录 数据结构——查找何为查找1. 查找表2. 关键字3. 查找方法效果评价指标——平均查找长度ASL(Average Search Length) 静态查找表1.顺序查找2.二分查找二分查找判定树 3.静态查找表—索引顺序表的查找索引顺序查找表的算法原理: 动态查找树表1. 二叉排序树2. 二叉…...

远程连接路由器:方法大全与优缺点解析
远程连接路由器的方式主要有以下几种,以下是每种方式的详细说明及其优缺点: 使用Web浏览器登录 方法:通过配置路由器的远程管理功能,允许用户通过互联网浏览器访问路由器的管理界面。用户只需输入路由器的公网IP地址或域名&#…...

NI USB-6009 DAQ采集卡拆解
所需设备: 1、NI USB-6009采集卡; 2、逻辑分析仪; NI USB-6009采集卡全貌: 性能参数: 内部照片: ADC芯片指标: 接线图: 差分模式采样: 采集过程中的SPI总线数据监控&a…...
详细分析Mysql临时变量的基本知识(附Demo)
目录 前言1. 用户变量2. 会话变量 前言 临时变量主要分为用户变量和会话变量 1. 用户变量 用户变量是特定于会话的,在单个会话内可以在多个语句中共享 以 符号开头在 SQL 语句中使用 SET 语句或直接在查询中赋值 声明和赋值 SET var_name value; -- 或者 SE…...

JS的五种事件函数,各自应用场景又分别是什么
在JavaScript中,常用的五种事件函数包括: 1. onclick:当用户点击某个元素时触发,适用于处理按钮点击、链接点击等场景。 2. onkeydown:当用户按下某个键盘的按键时触发,适用于处理键盘输入相关的操作&#…...

电脑想加个WIFI功能,怎么选!
在快速发展的物联网和智能家居时代,Wi-Fi模块作为连接各类智能设备与互联网的桥梁,其重要性不言而喻。而为了让这些模块能够适应各式各样的应用场景,不同的接口技术应运而生。今天,我们就来深入浅出地探讨几种常见的Wi-Fi模块接口,包括它们的工作原理、特点以及适用场景,…...

机器学习——决策树
决策树 决策树可以理解为是一颗倒立的树,叶子在下端,根在最上面 一层一层连接的是交内部节点,内部节点主要是一些条件判断表达式,叶子叫叶节点,叶节点其实就是最终的预测结果,那么当输入x进去,…...
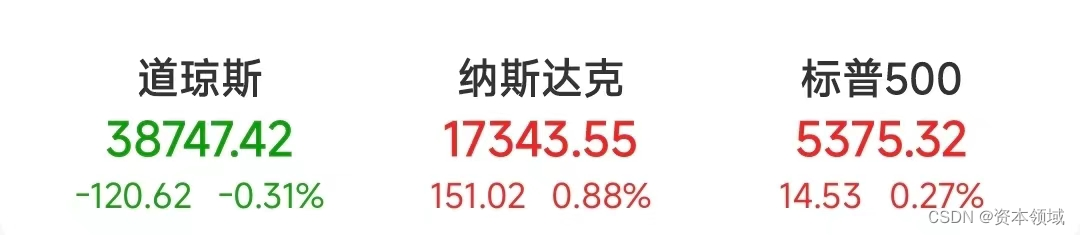
弘君资本:苹果股价暴涨,创历史新高!
当地时间6月11日,美股三大指数涨跌纷歧,标普500指数与纳指再创新高。 到收盘,道指跌0.31%,纳指涨0.88%,标普500指数涨0.27%。 苹果大涨逾7%创前史新高。美联储开端召开6月货币方针会议,周三发布利率决定。…...

web前端拖拽工具:探索其复杂性、困惑度与爆发度
web前端拖拽工具:探索其复杂性、困惑度与爆发度 在Web前端开发中,拖拽功能是一项常见且复杂的需求。拖拽工具可以帮助开发者更高效地实现这一功能,但同时也带来了一定的困惑和挑战。本文将从四个方面、五个方面、六个方面和七个方面对Web前端…...

Web前端数据驱动视图的深度解析
Web前端数据驱动视图的深度解析 在Web前端开发中,数据驱动视图的概念日渐重要,它不仅改变了传统的开发模式,更使得页面动态化和交互性得到了极大的提升。然而,对于许多初学者和开发者来说,如何深入理解和应用这一概念…...

HTML5的新语义化标签
HTML5 引入了一系列新的语义化标签,这些标签为网页内容提供了更明确的含义,有助于改善网页的可访问性和搜索引擎优化(SEO)。以下是一些主要的 HTML5 语义化标签: <article>: 表示页面、应用或网站中…...

周一美股集体低开后转涨,早盘仅道指小幅下跌,英伟达跌超3%后转涨超1%
美国非农就业报告发布“次日”,三大股指低开,但早盘均成功转涨。美股七姐妹涨跌各异,苹果WWDC大会今晚开幕,但早盘转跌,一度跌超1%;1拆10股正式生效的英伟达盘初曾跌超3.2%,开盘1.5小时内首次转…...
Phybers:脑纤维束分析软件包
摘要 本研究提供了一个用于分析脑纤维束数据的Python库(Phybers)。纤维束数据集包含由表示主要白质通路的3D点组成的流线(也称为纤维束)。目前已经提出了一些算法来分析这些数据,包括聚类、分割和可视化方法。由于流线的几何复杂性、文件格式和数据集的大小(可能包…...
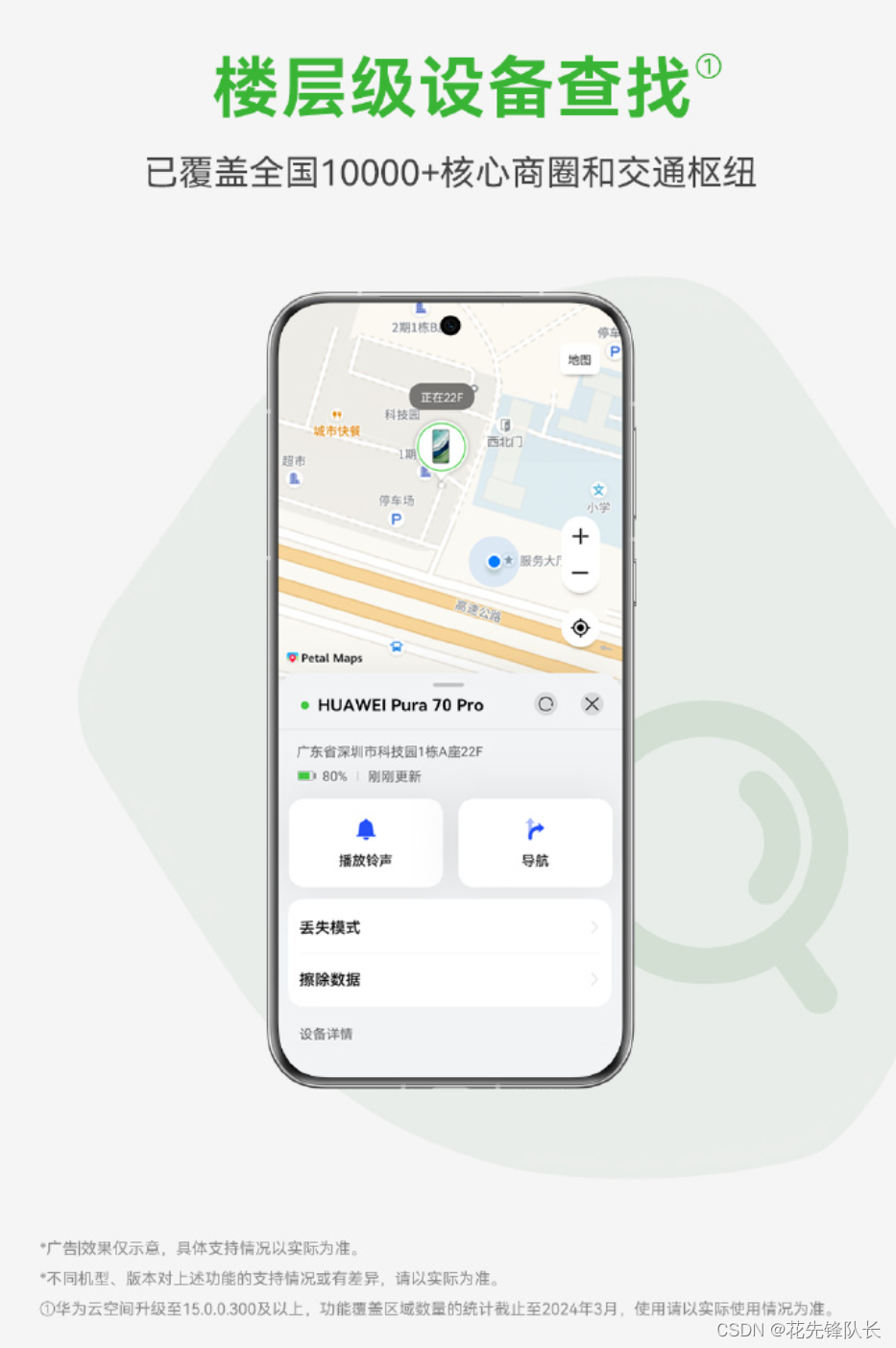
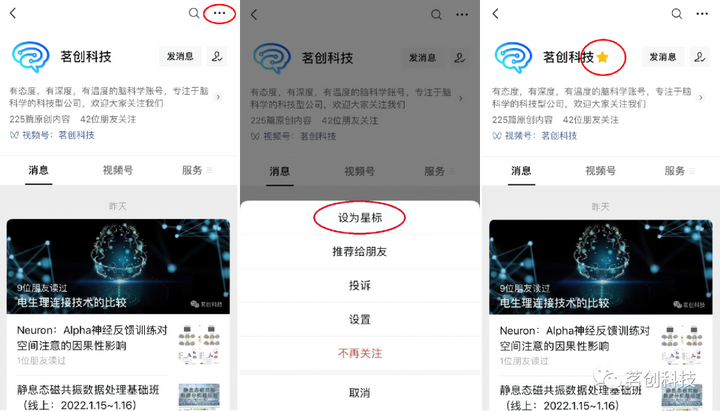
手机丢失不惊慌,华为手机已升级至楼层级设备查找!
出门总是丢三落四,手机丢了怎么办?不要怕,只要你的华为手机升级至云空间新版本,就可以进行楼层级设备查找,现在可以查看到具体的楼层了! 之前有手机丢失过的朋友,肯定有相似的经历,…...

SpringBoot 的多配置文件
文章目录 SpringBoot 的多配置文件spring.profiles.active 配置Profile 和 ActiveProfiles 注解 SpringBoot 的多配置文件 spring.profiles.active 配置 默认情况下,当你启动 SpringBoot 项目时,会在日志中看到如下一条 INFO 信息: No act…...
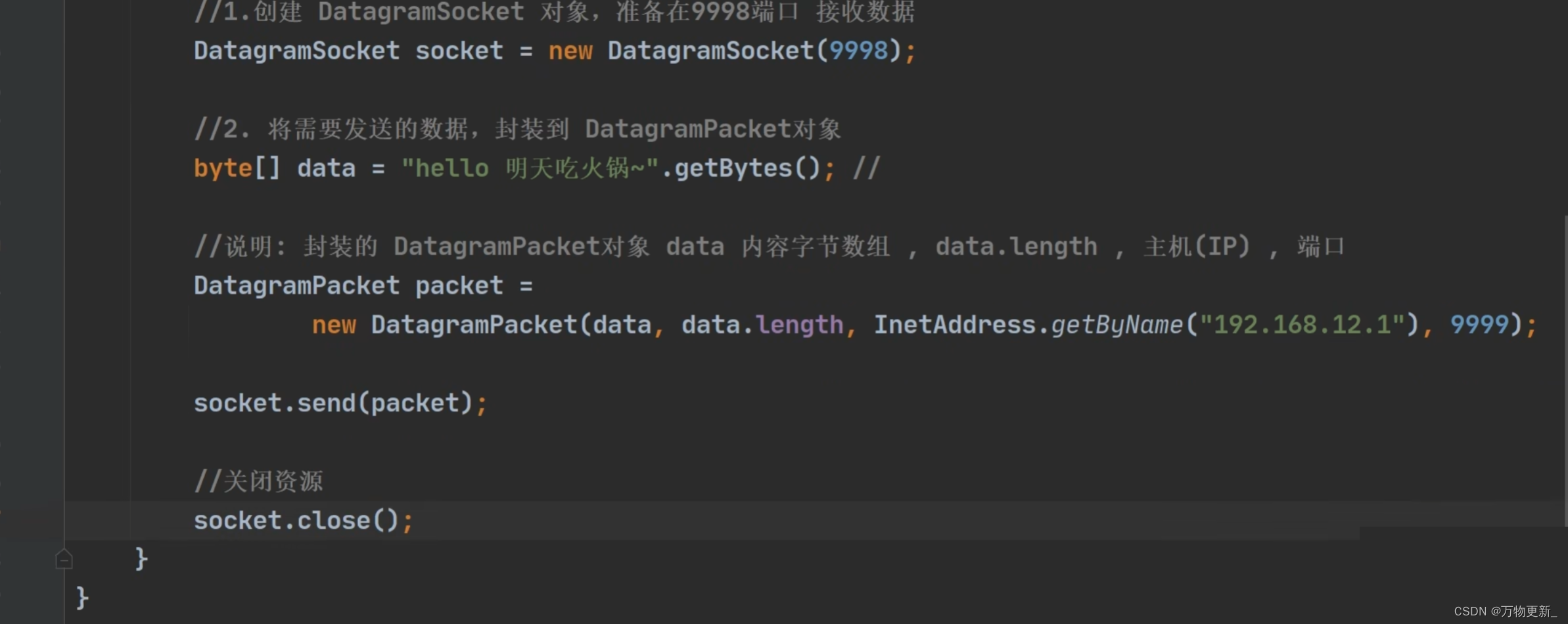
[Java基础揉碎]网络相关概念
目录 网络通信 网络 ip地址 编辑 域名 编辑 网络协议 TCP和UDP 网络编程比较重要的的InetAddress类 Socket 编辑 tcp字节流编程 案例一 案例二编辑 案例三 网络上传文件 编辑编辑 编辑 netstat tcp网络通信客户端也是通过端口和服务端进行通讯的…...
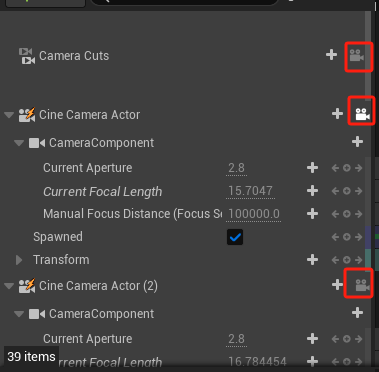
UE5 Sequencer 使用指导 - 学习笔记
https://www.bilibili.com/video/BV1jG411L7r7/?spm_id_from333.337.search-card.all.click&vd_source707ec8983cc32e6e065d5496a7f79ee6 Sequencer 01 1.1 调整视口 调整窗口数量 调整视口类型为Cinematic视口 视口显示网格,或者条件参考线 1.2 关卡动画与…...

Web前端项目源码:深入解析与未来探索
Web前端项目源码:深入解析与未来探索 Web前端项目源码,如同隐藏在数字世界中的宝藏,蕴含着丰富的技术与智慧。它是构建现代网页应用的核心,也是实现用户交互和界面呈现的关键所在。本文将从四个方面、五个方面、六个方面和七个方…...
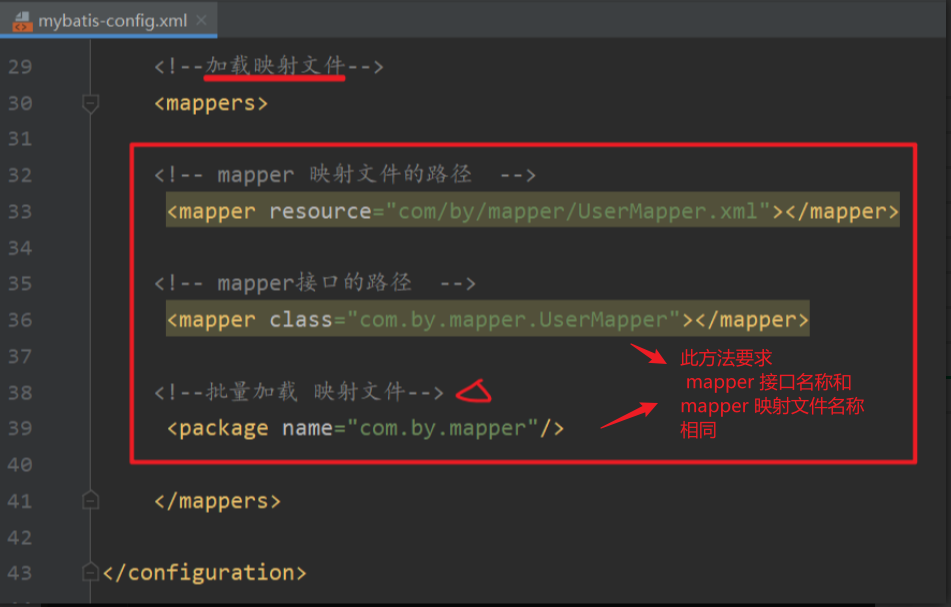
MyBatis的配置文件,即:src->main->resources的配置
目录 1、properties 标签 1.1 mybatis-config.xml 1.2 db.properties 1.3 在SqlMapConfig.xml 中 引入数据库配置信息 2、typeAliases 标签 2.1 定义别名 2.2 使用别名 3、Mappers标签 作用:用来在核心配置文件中引入映射文件 引入方式,有以下…...

completefuture造成的rpc重试事故
前言 最近经历了一个由于 completefuture 的使用,导致RPC重试机制触发而引起的重复写入异常的生产bug。复盘下来,并非是错误的使用了completefuture,而是一些开发时很难意识到的坑。 背景 用户反馈通过应用A使用ota批量升级设备时存在概率…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...
