6.每日LeetCode-数组类,找到所有数组中消失的数字
题目
448找到所有数组中消失的数字.go 给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。 示例 1: 输入:nums = [4,3,2,7,8,2,3,1] 输出:[5,6] 示例 2: 输入:nums = [1,1] 输出:[2] 提示: n == nums.length 1 <= n <= 105 1 <= nums[i] <= n 进阶:你能在不使用额外空间且时间复杂度为 O(n) 的情况下解决这个问题吗? 你可以假定返回的数组不算在额外空间内。
解法
package mainimport "fmt"// 448找到所有数组中消失的数字.go
// 给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
// 示例 1:
// 输入:nums = [4,3,2,7,8,2,3,1]
// 输出:[5,6]
// 示例 2:
// 输入:nums = [1,1]
// 输出:[2]
// 提示:
// n == nums.length
// 1 <= n <= 105
// 1 <= nums[i] <= n
// 进阶:你能在不使用额外空间且时间复杂度为 O(n) 的情况下解决这个问题吗? 你可以假定返回的数组不算在额外空间内。// 使用 map 非常简单,但不满足进阶
func findDisappearedNumbers1(nums []int) []int {slice := make([]int, 0)mp := make(map[int]bool, len(nums))for _, val := range nums {mp[val] = true}for i := 1; i <= len(nums); i++ {if _, ok := mp[i]; !ok {slice = append(slice, i)}}return slice
}// 1. 范围为1到n,
// 2. 将每个数-1取模, 如果按顺序就得到该值应该在的index处, 将该index处的值+n, 那么在该范围的值都应该大于n
// 3. 此时我们找出值小于n的index, 即为缺失的数字
// 时间复杂的O(n) 空间复杂度O(1)
func findDisappearedNumbers(nums []int) []int {var rst []intn := len(nums)for i := 0; i < n; i++ {idx := (nums[i] - 1) % nnums[idx] = nums[idx] + n}for i := 0; i < n; i++ {if nums[i] <= n { // 因为n也可能缺失,所以是小于等于rst = append(rst, i+1) // 该坐标值+1 就是该值, 因为是1到n,而坐标从0开始}}return rst
}func main() {nums := []int{4, 3, 2, 7, 8, 2, 3, 1}fmt.Println(findDisappearedNumbers(nums))
}
相关文章:

6.每日LeetCode-数组类,找到所有数组中消失的数字
题目 448找到所有数组中消失的数字.go 给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。 示例 1: 输入:nums [4,3,2,7,8,2,…...

【Three.js】知识梳理十:Three.js纹理贴图
1. 纹理贴图 在Three.js中,纹理贴图是一种将二维图像贴到三维物体表面的技术,以增强物体的视觉表现。纹理贴图可以使物体表面更加真实、细腻,为场景增色不少。 在Three.js中,纹理贴图的加载主要通过THREE.TextureLoader类实现。…...

mysql order by后跟case when
在SQL中,ORDER BY子句用于对查询结果进行排序。当在ORDER BY后面使用CASE语句时,它的原理是:根据CASE语句中定义的条件和结果,为查询结果集中的每一行生成一个临时的排序值。然后,根据这些排序值对结果集进行排序。 具…...

数字孪生赋能的智慧园区物联网云平台建设方案(97页PPT)
方案介绍: 本方案通过数字孪生技术赋能智慧园区物联网云平台,实现了园区的智能化管理、优化资源配置、提高运营效率等目标。同时提升园区的安全性、环保性和可持续性。最后,该方案还充分考虑了系统的可扩展性、安全性和可靠性,为…...

TikTok小店运营策略
TikTok,作为一款全球知名的短视频社交平台,其用户基数庞大且日活跃用户持续增长,为商家提供了巨大的商机。欧洲作为TikTok的重要市场之一,其小店功能为商家提供了一个展示和销售产品的新渠道。本文将探讨如何有效地运营TikTok小店…...

Docker面试整理-如何查看和管理Docker容器的日志?
管理和查看 Docker 容器的日志是 Docker 容器管理的重要部分,有助于监控应用的行为和诊断问题。Docker 提供了几种方法来查看和管理容器日志。 查看容器日志 要查看 Docker 容器的日志,你可以使用 docker logs 命令。这个命令会打印容器的 STDOUT 和 STDERR 输出,这是大多数…...

Java从放弃到继续放弃
并发编程 为什么需要多线程? 由于硬件的发展,CPU的核数增多,如果仍然使用单线程对CPU资源会造成浪费。同时,单线程也会出现阻塞的问题。所以,选择向多线程转变。 多线程的使用使得程序能够并行计算,提高计…...
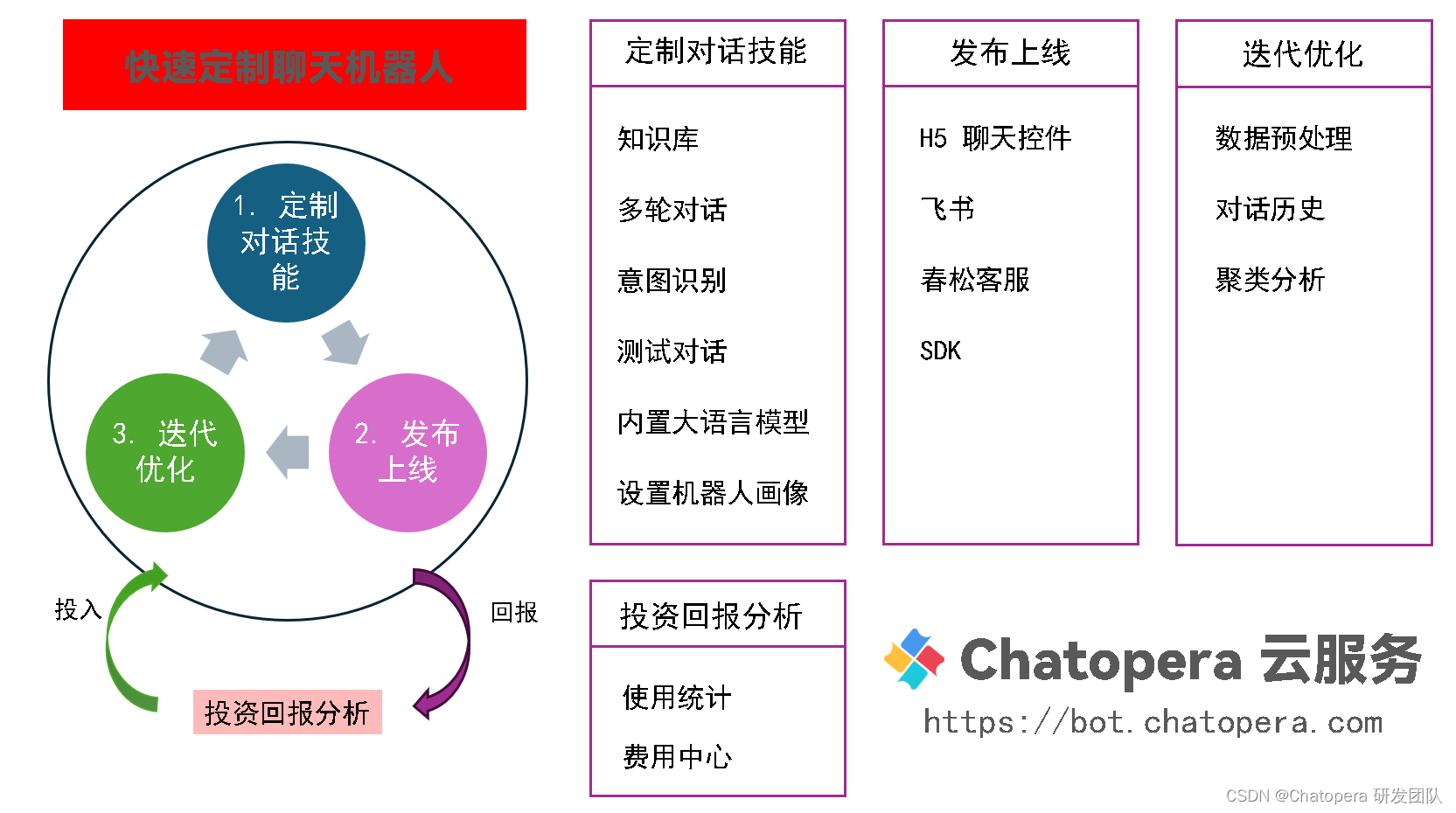
上传文件生成聊天机器人,实现客服、办公自动化智能体 | Chatopera
从谈论聊天机器人,到谈论智能体,是目前人工智能最炙手可热的话题,这两年最大的变化是大语言模型的应用。聊天机器人曾经很难定制,往往局限于个别行业,同时也只有行业内的领导者、头部企业能定制。比如银行、金融证券、…...
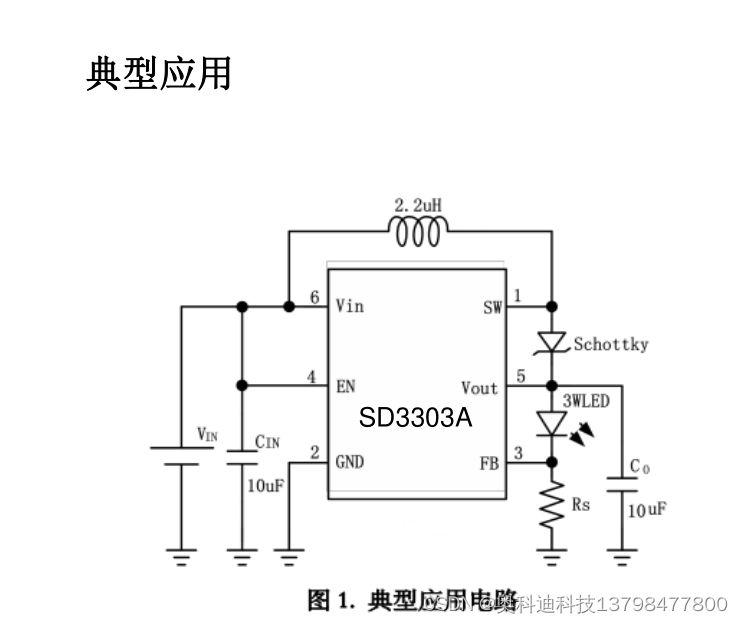
SD3303A 大功率高亮度LED驱动芯片IC
一般描述 SD3303A是一款大功率高亮度LED驱动芯片,可以提供1A的电流驱动3W的LED。具有高效率,低功耗等特点,适用于电池供电的LED照明设备。 SD3303A具有开路保护和过温保护。 SD3303A需要使用两颗10uF(或者更大)的瓷片电容,来保…...

站易WordPress
站易WordPress是一家专业提供网站建设和运营服务的公司。他们提供的服务包括企业官方网站建设、网站运营维护、网站托管、网站优化、跨境独立站建站、外贸网站建设以及海外多语言网站建设等。 此外,站易还提供使用现成的WordPress模板,这样可以快速且低…...

windows下JDK1.8安装
windows下JDK1.8安装 本文假设你知道了解基本的windows系统操作。 在Windows系统下安装JDK 1.8(Java Development Kit)的步骤如下: 步骤1:下载JDK 1.8 打开浏览器并访问Oracle JDK下载页面。https://www.oracle.com/java/technol…...
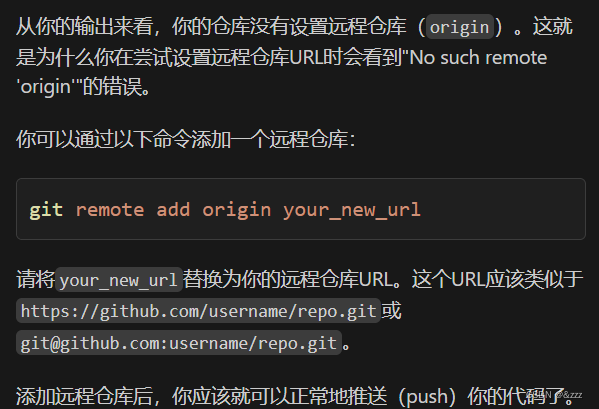
怎么修改Visual Studio Code中现在github账号
git config --global user.name “你的用户名” git config --global user.email “你的邮箱” git config --global --list git push -u origin your_branch_name git remote add origin...

戴尔R720服务器(3)组RAID
今天收到7块硬盘,现在共有8块硬盘了,找了个视频学习了怎么使用阵列卡组RAID并记录。 视频参考:【戴尔服务器添加RAID5热备盘hotspare】 阵列卡组RAID5 开始 连接iDRAC控制台服务器开机按F2进入BIOS选择Device Settings …...
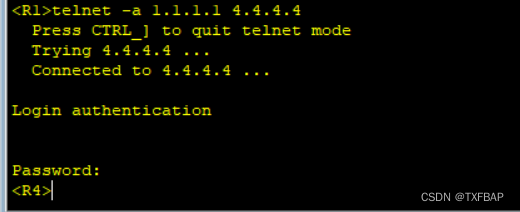
eNSP学习——配置高级的访问控制列表
目录 主要命令 原理概述 实验目的 实验内容 实验拓扑 实验编址 实验步骤 1、基本配置 2、搭建OSPF网络 3、配置Telnet 4、配置高级ACL控制访问 需要eNSP各种配置命令的点击链接自取:华为eNSP各种设备配置命令大全PDF版_ensp配置命令大全资源-…...

oracle的bitmap索引是什么
Oracle的Bitmap索引是一种特殊的索引类型,主要用于处理那些数值稀疏(low-cardinality,低基数)的字段,特别是那些值不经常改变的字段。以下是关于Bitmap索引的详细解释: 定义: Bitmap索引是一种…...

「前端+鸿蒙」鸿蒙应用开发-TS接口-特殊用途
在 TypeScript 中,接口除了定义对象的结构之外,还有一些特殊用途,这些用途使得接口成为一种灵活的工具,用于提高代码的可维护性和可扩展性。 TS快速入门-接口-特殊用途 1. 定义函数类型 接口可以用来定义函数的类型,…...
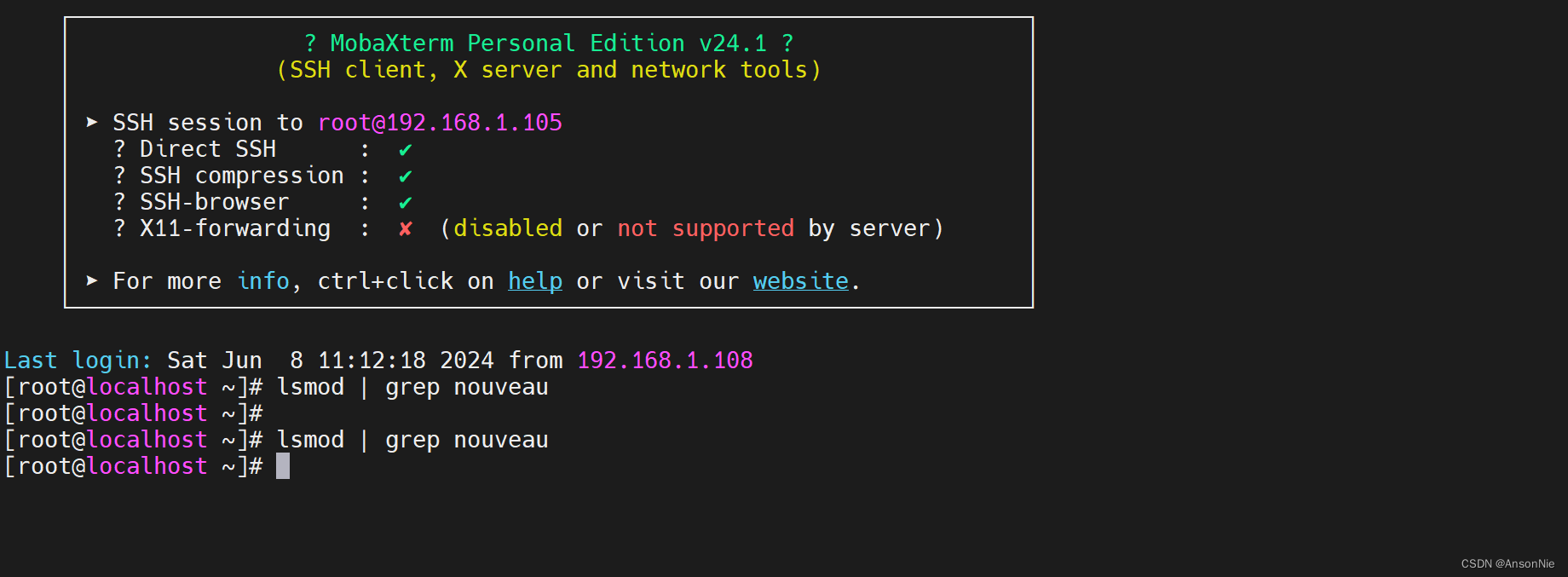
Centos7系统禁用Nouveau内核驱动程序【笔记】
在CentOS系统中,Nouveau是开源的NVIDIA显卡驱动程序,但它与NVIDIA的官方驱动程序NVIDIA Proprietary Driver存在兼容性问题。 如果你想要禁用Nouveau并使用NVIDIA官方驱动,可以按照以下步骤操作: 1、创建一个黑名单文件以禁用No…...

Vue 面试通杀秘籍
理论篇: 1. 说说对 Vue 渐进式框架的理解(腾讯医典) a) 渐进式的含义: 主张最少, 没有多做职责之外的事 b) Vue 有些方面是不如 React,不如 Angular.但它是渐进的,没有强主张, 你可以在原有…...
聚焦新版综合编程能力面试考查汇总
目录 一、业务性编程和广度能力考查 (一)基本定义 (二)必要性分析 二、高频考查样题(编程扩展问法) 考题1: 用java 代码实现一个死锁用例,说说怎么解决死锁问题?(高…...

[工具探索]英寸vs毫米下常见尺寸排版
文章目录 常见尺寸1. 照片尺寸2. 纸张尺寸3. 显示器和电视屏幕尺寸4. 手机屏幕尺寸5. 笔记本电脑屏幕尺寸6. 其他设备尺寸 换算公式换算方法常见照片尺寸对比表国际标准ISO(216)纸张尺寸 什么是英寸? 英寸(英语:inch&a…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
