鉴源论坛 · 观模丨模型检查综述
作者 | 李建文 华东师范大学软件工程学院博导
版块 | 鉴源论坛 · 观模
01 模型检查的历史
模型检查是一种起源于20世纪70年代末的形式化验证技术。该技术最初由Edmund M. Clarke、E. Allen Emerson和Joseph Sifakis提出,他们因在模型检查领域的贡献而获得了2007年的图灵奖。模型检查的提出最初是为了对并发和分布式系统做自动化验证,这些系统越来越复杂,手动验证则变得越来越困难。模型检查涉及系统地探索系统的所有可能状态,并检查每个状态是否满足某些属性。
在早期阶段,模型检查可以通过显示地计算Kripke结构上的不动点(针对CTL描述的性质) [1]或者是在由模型和LTL性质构造的乘积自动机上做状态搜索 [2]来完成。尽管这些技术非常直观且易于理解,但它们处理大型系统的能力非常有限,现在它们已经被以BDD [3]和SAT求解器 [4]为计算核心的符号模型检查技术所取代。事实上,基于SAT求解器的模型检查技术是目前最有前景的自动化验证技术。目前最先进的基于SAT求解器的模型检查技术包括BMC [5],IMC [6],IC3/PDR [7],和CAR [8]。
模型检查已被应用于各种系统,包括硬件电路、通信协议、操作系统和软件程序。它已被用于在部署之前检测系统中的错误和缺陷,这可以在开发过程中节省时间和金钱。今天,模型检查是一个活跃的研究和开发领域,研究人员正在不断努力,以提高其拓展性、准确性和可用性。
02 模型检查问题描述
模型检查问题是说:给定一个模型M,或者说一个状态迁移系统,如何判断M是否满足安全性质P。在具体算法实现中,我们往往是从初始状态I出发,判断┐P代表的状态是否可达,即是否所有I可达的状态都是满足安全性质P的。如果我们在算法中找到了反例,即从I出发,经过一系列状态,可以到达┐P,则我们返回反例,用以说明安全性质P不成立;如果我们找到了一个不变式,即证明了从I出发,所有可达的范围都在一个满足P的状态集合中,则我们返回验证通过,安全性质P成立。下面我们先简要介绍几个常见的模型检查算法。
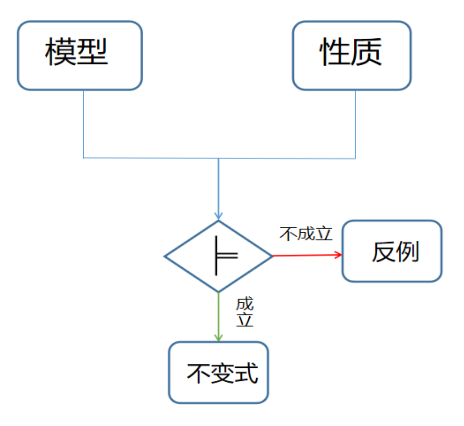
图1 模型检查问题示例图
03 模型检查算法介绍
3.1 Bounded Model Checking (BMC)
BMC是一个简单但是高效的模型检查算法,类似于图搜索中的广度优先搜索。BMC从初始状态出发,先判断是否可以直接一步转移到┐P,也就是不安全的状态中,若可以,则找出了一个长度为1的反例;若不行,则说明在初始状态一步的范围内,安全性质成立,接着,BMC增大步数,判定从初始状态出发,是否可以两步转移到┐P,同样地,若可达则返回反例,若不可达,则继续增大步数,直到找到反例或者达到限定的时间为止。
如下图所示,从S0出发,先确定一步可达的S1和S2满足性质,接着增大步数,确定两步可达的S3满足性质,再确定三步可达的S4和S5满足性质,最终步数为4时,检查出四步可达的S6不满足性质,从而得到反例。
使用BMC算法可以很快地找到长度最短的反例,但是它的局限性也很大,假设BMC在k步之内找不到反例,这只能说明初始状态k步可达的状态满足安全性质,而不能证明初始状态可达的状态都是满足安全性质的,也就是说,BMC只适用于反例的寻找,而不适合证明模型满足安全性质。
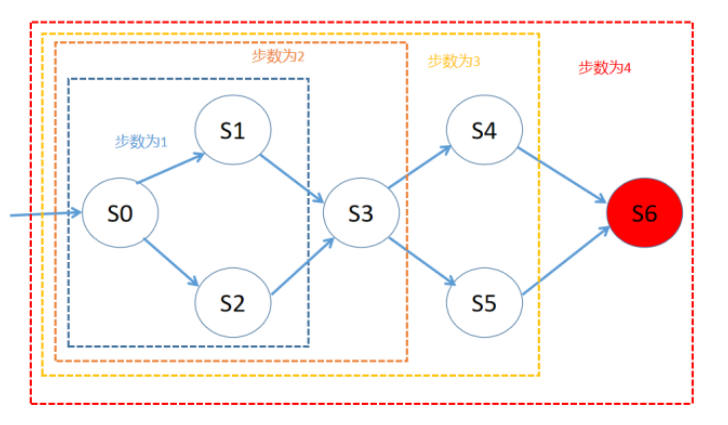
图2:BMC算法示例图
3.2 Interpolation Model Checking (IMC)
IMC是在BMC的基础上改进来的模型检查算法,它不仅可以查找反例,也可以证明模型是满足安全性质P的,弥补了BMC算法的缺陷。
简要地说,在查找反例上,IMC和BMC一样,都是靠确定从初始状态出发,┐P代表的非安全状态是否是k步可达的,如果是,则找到了反例,若不是,则继续增大k的值。和BMC不同的是,对于每一个步数k,IMC都维持了一个初始状态k步之内可达的状态的超集R,即R里面也包含了一些其他的状态,且R里面的元素都满足安全性质,在寻找反例的过程中,IMC不断扩大集合R,若在某个时刻,R不能被扩大,即R里面的元素只能转移到R里面,则我们找到了一个不变式,即证明了从初始状态出发,可达的所有状态都是满足安全性质的,从而证明了模型是满足安全性质P的。
如下图所示,从初始状态S0出发,我们找到了一个状态集合R,使得S0可达的状态S1、S2和S3都在集合R中,且R中的元素都满足安全性质,因此我们证明了模型是满足安全性质的,集合R就是证据。
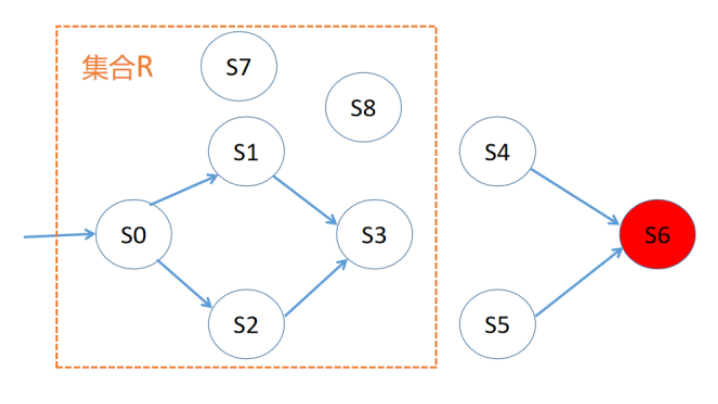
图3 IMC算法示例图
3.3 Property Directed Reachability (PDR)
PDR是一个较为复杂的模型检查算法,简要地说,它维持了一个满足安全性质P的状态集合的序列F,其中F(0)是初始状态I,而F(1)则是初始状态一步之内可达的集合的超集,即它里面除了有初始状态一步之内可达的状态,也包含了一些其他的状态,以此类推,后面每一个F(i)集合都是前一个F(i-1)集合的一步之内可达的集合的超集,PDR算法不断地在F(i)集合中寻找那些可以一步转移到┐P的元素S,若F(i)中的其他元素可以一步转移到S,则PDR接着判断F(i-1)中的元素可不可以两步转移到S,以此类推,若在F(0),即初始状态中,有元素可以多步转移到S,则找到了一个反例,即性质P不成立,如果在这个过程中,我们找到一个F(i)集合,使得它里面的元素都不能转移到S,则我们可以把S从这个集合及它之前的集合中删除,我们不断重复这个过程,如果在某一步,存在某个F(i)使得F(i)=F(i-1),即F(i-1)里面的状态只能转移到F(i-1)里面时,我们就找到了一个不变式,即所有初始状态可达的状态都满足了性质P,证明了性质P成立。
如下图所示,在集合F(i+1)中,状态S4可以一步转移到非安全状态S6,但是集合F(i+1)中的其他集合不能转移到S4,因此我们把S4从Fi+1及其之前的集合中删除,删除S4后,我们发现集合F(i+1)和F(i)相等,即此时F(i)里面的状态只能转移到F(i)里面,因为F(i)是初始状态可达的状态的超集,从而初始状态可达的元素都在F(i)中,因此模型的安全性质就得到了满足,F(i)就是证据。
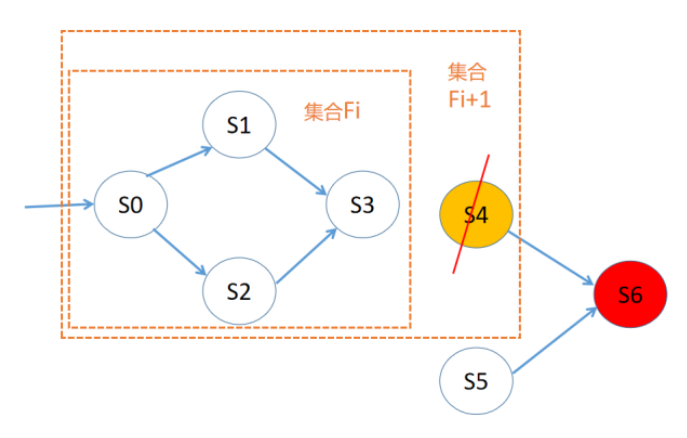
图4 PDR算法示例图
3.4 Complementary Approximate Reachability (CAR)
CAR算法也是一个较为复杂的模型检查算法,可以有两个搜索方向(Forward CAR和Backward CAR),后续我们以Backward CAR为例。CAR维护了两个序列,B序列和F序列,F序列是从初始状态I出发可达的状态的子集的集合,B序列则是可以到达非安全状态的!P的状态的超集的集合,且F(0)= I , B(0)= !P。维护子集与超集的原因是F序列和B序列都是动态的,Fi的元素会随着算法运行不断增多,子集会越来越接近原集。而B(i)的元素则会不断减少,超集也会越来越接近原集。CAR算法就是不断地去做类似的SAT调用,然后根据结果去更新F和B序列。例如CAR算法会不断地通过SAT来判断某个状态s能否一步转移到B(i),若成立,则可以拿到s的一个后继状态s'并把其加入到F序列,随后CAR则递归询问s'是否可以转移到B(i-1);若不成立,CAR则会拿到一个uc(最小不满足核),并把这个uc来更新B(i+1)。
若存在某个B(i),其是所有B(j) (j < i) 的并集的子集,那么模型是安全的。安全性条件生效表明B序列不会再扩大,即使继续扩展B序列,新的B(i+1)中的元素,只会是下标更小的B(i)中出现过的元素,这意味着初始状态I不可能到达B(0),因此模型是安全的。此时从B0至B(i)的并集构成了一个不变式。如果某一个状态空间F(i)中,存在一个状态s,此状态属于非安全状态!P,则得到一条以I为起点,状态s为终点路径,这条路径是待验证性质的反例,将被返回。
如下图所示,我们发现集合B(i+1)包含在所有B(j) (j < i+1) 的并集中,因此安全性条件生效,B(j) (j < i+1) 的并集就是我们要找的不变式(安全性证明)。
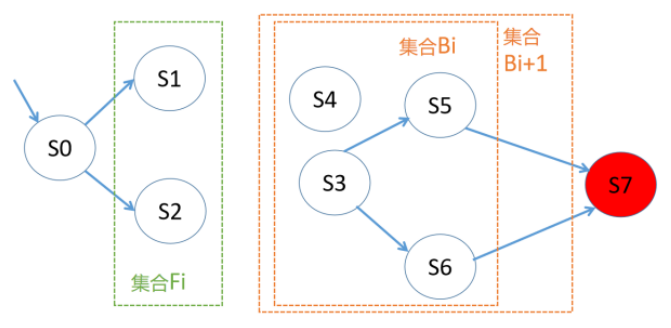
图5 CAR算法示例图
参考文献:
[1] E. Clarke and H. Schlingloff, “Model checking,” in Handbook of Automated Reasoning, A. Robinson and A. Voronkov, Eds. MIT Press, 2001, pp. 1635–1790.
[2] O. Kupferman, N. Piterman, and M. Y. Vardi, “An automata-theoretic approach to infinite-state systems,” in Time for Verification: Essays in Memory of Amir Pnueli, Z. Manna and D. A. Peled, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010, pp. 202–259.
[3] K. L. McMillan, Symbolic Model Checking. Boston, MA: Springer US, 1993.
[4] Y. Vizel, G. Weissenbacher, and S. Malik, “Boolean satisfiability solvers and their applications in model checking,” Proceedings of the IEEE, vol.103, no. 11, pp. 2021–2035, 2015.
[5] A. Biere, A. Cimatti, E. Clarke, and Y. Zhu, “Symbolic model checking without BDDs,” in Tools and Algorithms for the Construction and Analysis of Systems (TACAS), W. R. Cleaveland, Ed. Berlin, Heidelberg: Springer Berlin Heidelberg, 1999, pp. 193–207.
[6] K. L. McMillan, “Interpolation and SAT-based model checking,” in Computer Aided Verification, W. A. Hunt and F. Somenzi, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2003, pp. 1–13.
[7] A. R. Bradley, “SAT-based model checking without unrolling,” in Verification, Model Checking, and Abstract Interpretation, R. Jhala and D. Schmidt, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2011, pp. 70–87.
[8] J. Li, R. Dureja, G. Pu, K. Y. Rozier, and M. Y. Vardi, “Simplecar: An efficient bug-finding tool based on approximate reachability,” in Computer Aided Verification, H. Chockler and G. Weissenbacher, Eds. Cham: Springer International Publishing, 2018, pp. 37–44.
相关文章:

鉴源论坛 · 观模丨模型检查综述
作者 | 李建文 华东师范大学软件工程学院博导 版块 | 鉴源论坛 观模 01 模型检查的历史 模型检查是一种起源于20世纪70年代末的形式化验证技术。该技术最初由Edmund M. Clarke、E. Allen Emerson和Joseph Sifakis提出,他们因在模型检查领域的贡献而获得了2007年的…...

Easy Deep Learning——池化层
池化是什么?它有什么作用? 还是草地的场景,把草地分成一块块的网格,数量还是太多了,如何继续简化输入数据呢? 这时候可以只取一块网格中所有的小草的大小形状的平均值或者最大值作为一个输入数据,这样就大…...

TryHackMe-VulnNet: Active(ez 域渗透)
VulnNet: Active VulnNet Entertainment在他们以前的网络中遇到了不好的时光,该网络遭受了多次破坏。现在,他们移动了整个基础架构,并再次聘请您作为核心渗透测试人员。您的目标是获得对系统的完全访问权限并破坏域。 这应该是我在thm打的最…...
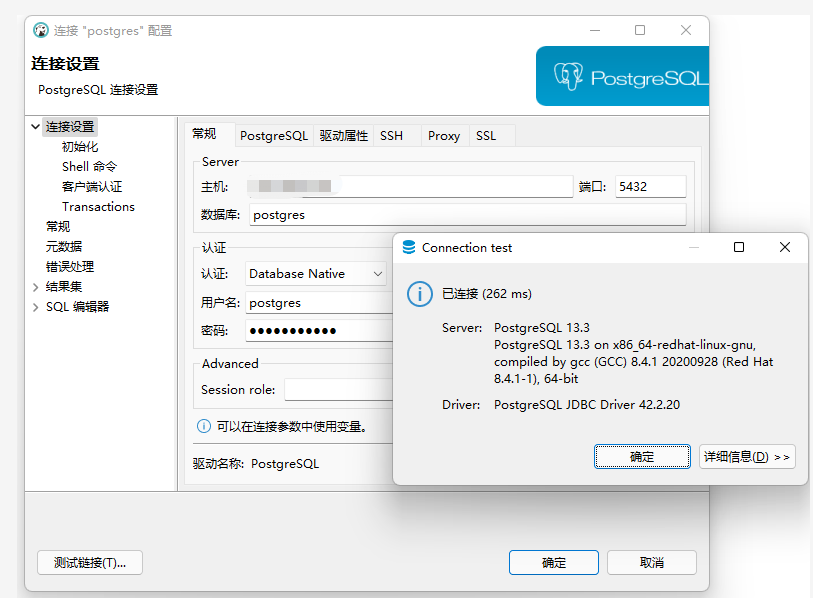
TencentOS Server 安装 PostgreSQL
TencentOS 简介 2019 年,随着腾讯公司外部客户的需求,以及公司开源协同战略的推进,tlinux 对外开源并进行了品牌升级,升级为 TencentOS Server。TencentOS 包含三大场景,分别如下: TencentOS Server&…...
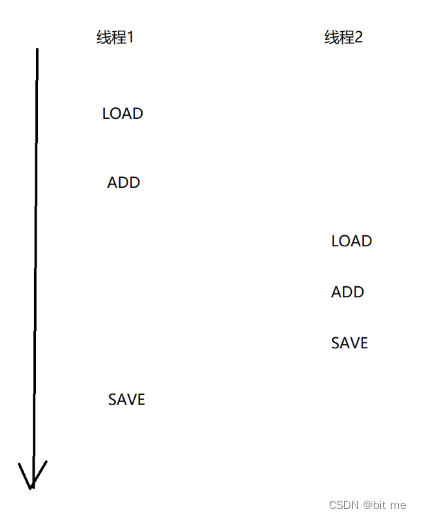
多线程的风险 --- 线程安全
✨个人主页:bit me👇 ✨当前专栏:Java EE初阶👇 ✨每日一语:低头赶路,敬事如仪;自知自心,其路则明。 目 录🍸一. 线程不安全🍹二. 线程不安全的原因…...

Linux信号详解
文章目录Linux信号什么是信号**从生活角度理解: **技术应用角度的信号进程的注意事项信号概念用kill -l命令可以察看系统定义的信号列表信号处理常见方式概览信号产生通过终端按键产生信号使用signal函数自定义SIGINT信号的处理方式使用sigprocmask函数阻塞2号信号和40号信号vo…...

JAVA使用POI操作EXCEL
设置公式totalRow.createCell(4).setCellFormula("SUM(E9:E35");// 执行公式wb.setForceFormulaRecalculation(true);合并单元格sheet.addMergedRegion(new CellRangeAddress(0, 0, 3, 7));单元格格式CellStyle cellStyle wb.createCellStyle();// 字体XSSFFont fon…...

只做笔记有必要买apple pencil吗?苹果笔的代替笔推荐
如果仅仅使用IPAD来进行打游戏和看剧的话,未免有些浪费。ipad的作用还是挺大的,可以用来做学习笔记,也可以用来做绘画,也可以用来做一些重要的内容。很多人都会认为,苹果的电容笔很好用,但是价格上要比一般…...
Hive---sqoop安装教程及sqoop操作
sqoop安装教程及sqoop操作 文章目录sqoop安装教程及sqoop操作上传安装包解压并更名添加jar包修改配置文件添加sqoop环境变量启动sqoop操作查看指定mysql服务器数据库中的表在hive中创建一个teacher表跟mysql的mysql50库中的teacher结构相同将mysql中mysql50库中的sc数据导出到h…...

【C++】register 关键字
文章目录一. 什么是寄存器?二. 为什么要存在寄存器?三. register 修饰变量一. 什么是寄存器? 我们都知道,CPU主要是负责进行计算的硬件单,但是为了方便运算,一般第一步需要先把数据从内存读取到CPU内&…...

剑指 Offer II 024. 反转链表
题目链接 剑指 Offer II 024. 反转链表 easy 题目描述 给定单链表的头节点 head,请反转链表,并返回反转后的链表的头节点。 示例 1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 示例 2: 输入:h…...

从Linux内核中学习高级C语言宏技巧
Linux内核可谓是集C语言大成者,从中我们可以学到非常多的技巧,本文来学习一下宏技巧,文章有点长,但耐心看完后C语言level直接飙升。 本文出自:大叔的嵌入式小站,一个简单的嵌入式/单片机学习、交流小站 从…...

详解Python的装饰器
Python中的装饰器是你进入Python大门的一道坎,不管你跨不跨过去它都在那里。 为什么需要装饰器 我们假设你的程序实现了say_hello()和say_goodbye()两个函数。 def say_hello():print "hello!"def say_goodbye():print "hello!" # bug hereif…...

k8s-Pod域名学习总结
k8s-Pod域名学习总结 大纲 k8s内置DNS服务 配置Pod的域名服务 CornDNS配置 默认Pod的域名 自定义Pod的域名 实战需求 1 Pod有自己的域名 2 集群内部的Pod可以通过域名访问其他的Pod 基础准备: 1 k8s 集群版本1.17 k8s内置DNS服务 k8s1.17安装完成后自动创建…...

0405习题总结-不定积分
文章目录1 不定积分的基本概念2 直接积分法-基本积分公式3 第一换元法-凑微分形式法4 第二类换元法5 分部积分求不定积分6 表格法积分7 有理函数求积分后记1 不定积分的基本概念 例1 f(x){x1,x≥012e−x12,x<0求∫f(x)dxf(x) \begin{cases} x1,\quad x\ge0\\ \frac{1}{2}e^…...

QT 常用控件类型命名参考
拟定的QT的控件命名规则:蛇形命名方式 控件类型开头,以下是QT控件类型命名的参考范例 Buttons Buttons起始字符串对象名称举例Push Buttonbuttonbutton_loginTool Buttontool_button / buttonbutton_switchRadio Buttonradio_button / radioradio_boy…...
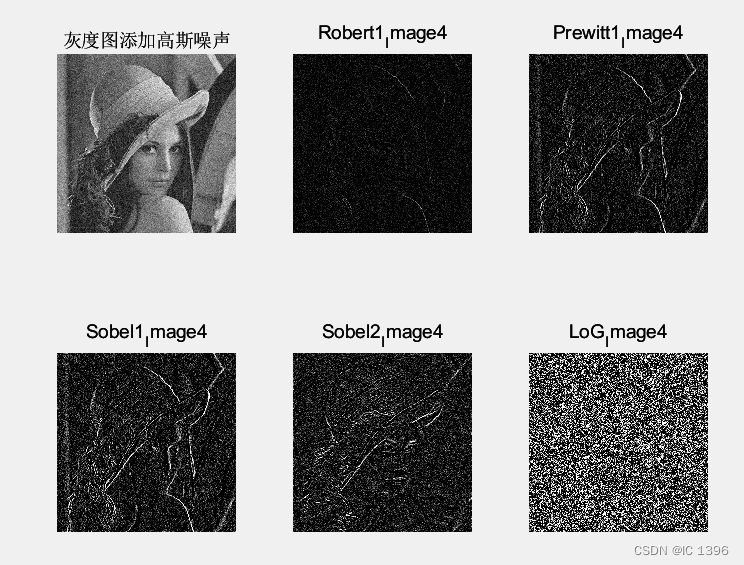
MATLAB与图像处理的那点小事儿~
目录 一、学习内容 二、matlab基本知识 三、线性点运算 四、非线性点运算,伽马矫正 五、直方图 1、直方图均衡化 (1)使用histep函数实现图像均衡化 (2)使用自行编写的均衡化函数实现图像均衡化 2、直方图规定…...
Java组个人题解)
第十四届蓝桥杯模拟赛(第三期)Java组个人题解
第十四届蓝桥杯模拟赛(第三期)Java组个人题解 今天做了一下第三期的校内模拟赛,有些地方不确定,欢迎讨论和指正~ 文章目录第十四届蓝桥杯模拟赛(第三期)Java组个人题解填空题部分第一题【最小数】第二题【E…...
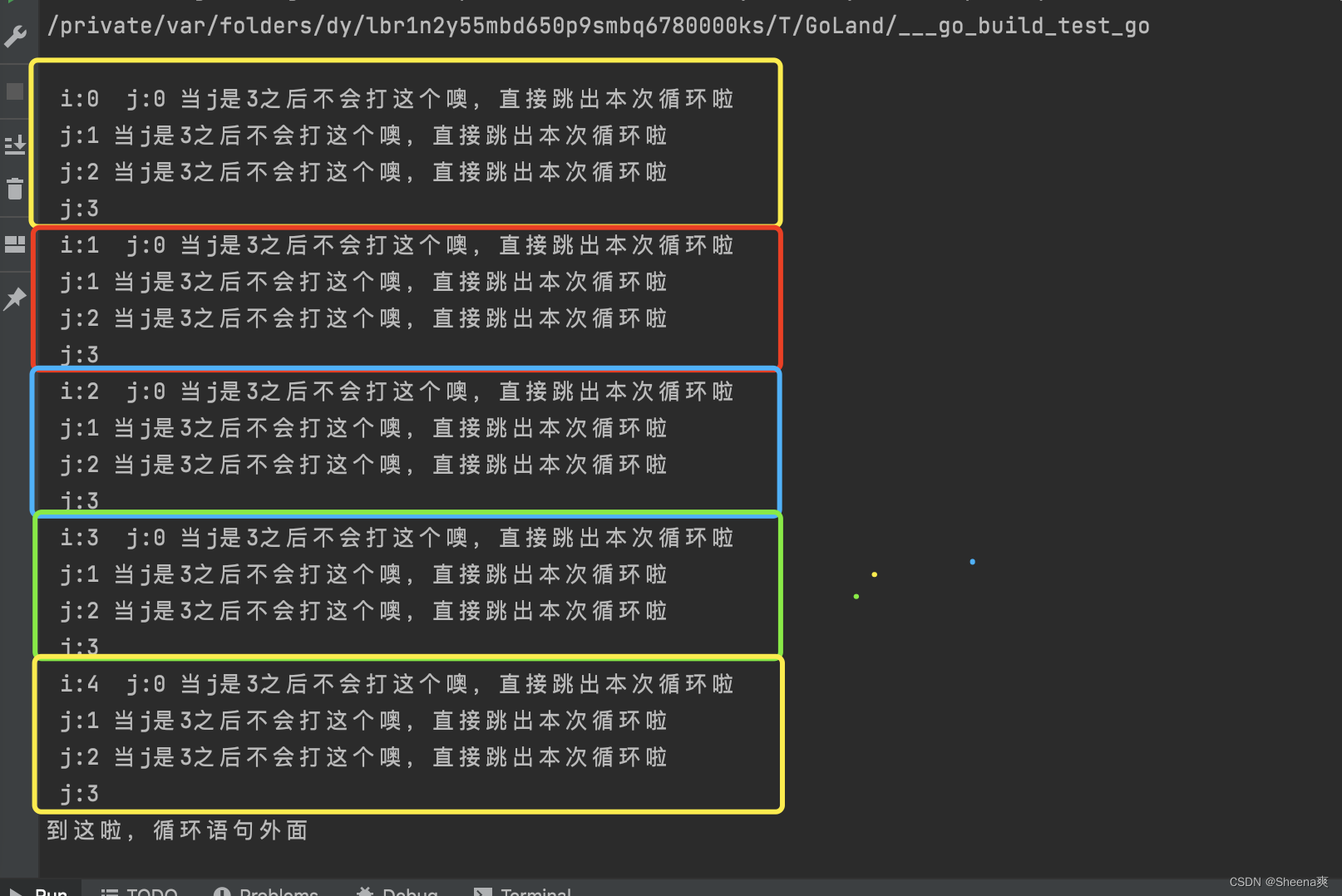
Go语言之条件判断循环语句(if-else、switch-case、for、goto、break、continue)
一、if-else条件判断语句 Go中的if-else条件判断语句跟C差不多。但是需要注意的是,Go中强制规定,关键字if和else之后的左边的花括号"{“必须和关键字在同一行,若使用了else if结构,则前段代码快的右花括号”}"必须和关…...
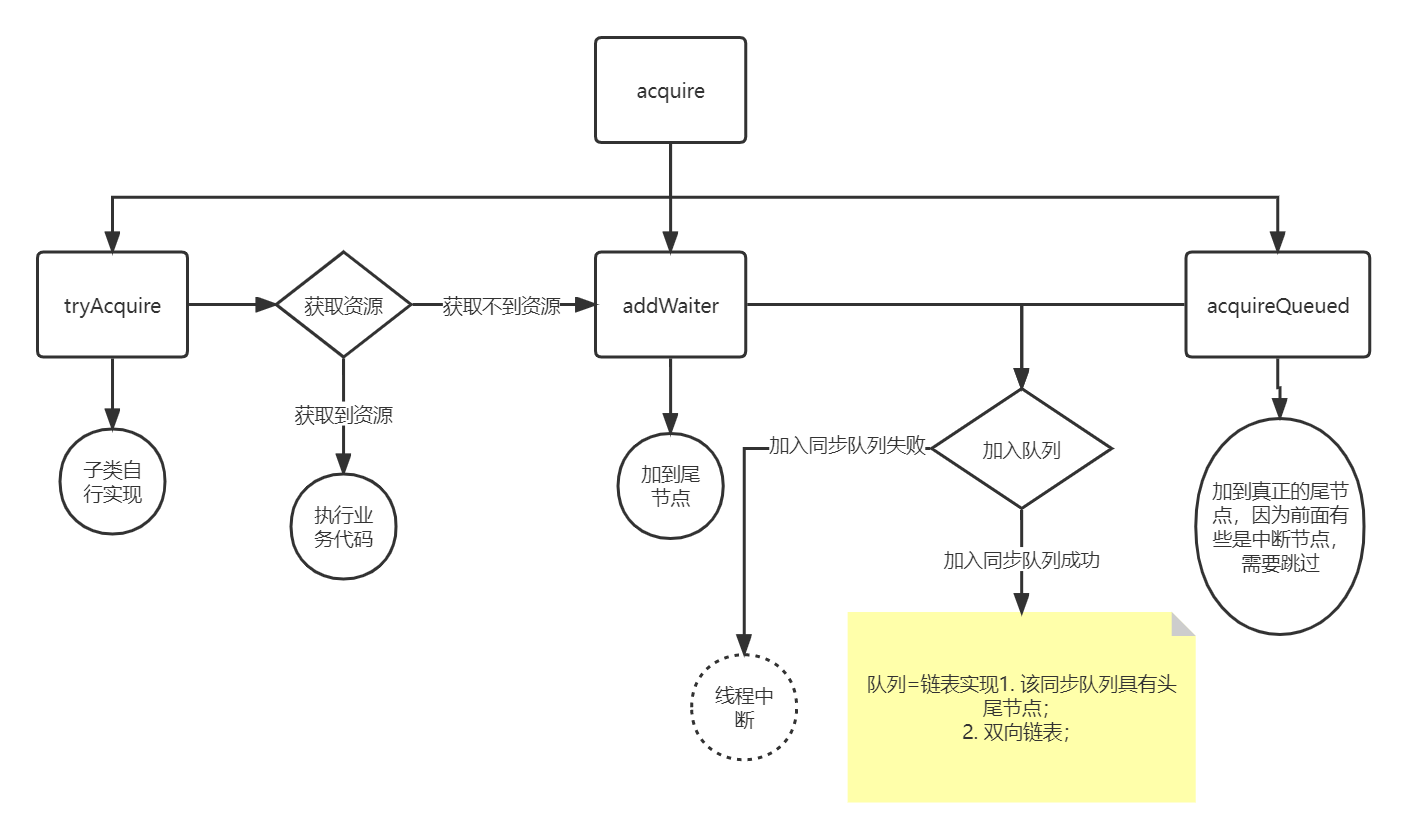
深入理解AQS
概念设计初衷:该类利用 状态队列 实现了一个同步器,更多的是提供一些模板方法(子类必须重写,不然会抛错)。 设计功能:独占、共享模式两个核心,state、Queue2.1 statesetState、compareAndSetSta…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
