数据结构 —— 堆
1.堆的概念及结构
堆是一种特殊的树形数据结构,称为“二叉堆”(binary heap)
看它的名字也可以看出堆与二叉树有关系:其实堆就是一种特殊的二叉树
堆的性质:
- 堆中某个结点的值总是不大于或不小于其父结点的值;
- 堆总是一棵完全二叉树
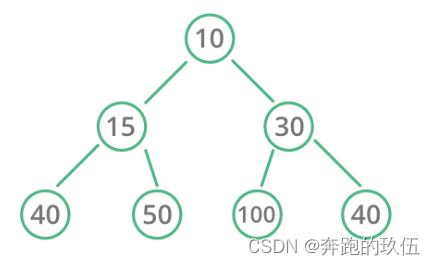
1.1大堆
大堆:
- 大堆的根节点是整个堆中最大的数
- 每个父节点的值都大于或等于其孩子节点的值
- 每个父节点的孩子之间并无直接的大小关系

1.2小堆
小堆:
- 小堆的根节点是整个堆中最小的数
- 每个父节点的值都小于或等于其孩子节点的值
- 每个父节点的孩子之间并无直接的大小关系
2.堆的实现
2.1使用数组结构实现的堆
由于堆是一个完全二叉树,所以堆通常使用数组来进行存储
使用数组的优点:
- 相较于双链表更加的节省内存空间
- 相较于单链表可以更好的算父子关系,并找到想要找的父子
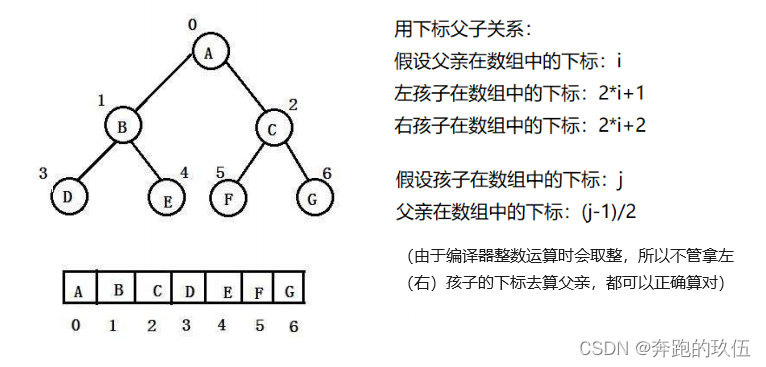
2.2堆向上调整算法
堆的向上调整(也称为堆化、堆的修复或堆的重新堆化)是堆数据结构维护其性质的关键操作之一
int arr = [ 15, 18, 19, 25, 28, 34, 65, 49, 37, 10]
小堆演示向上调整算法演示过程
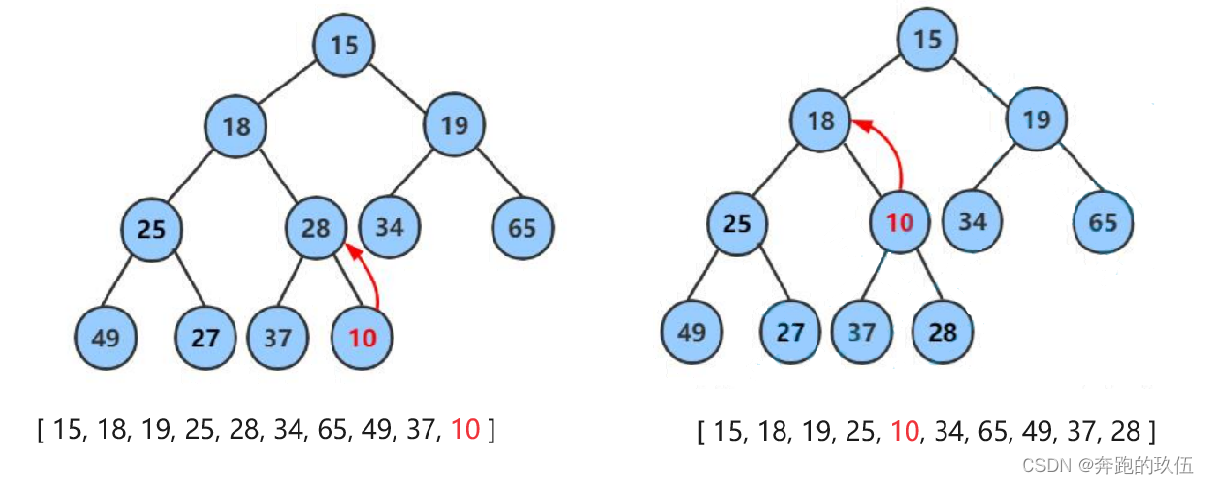
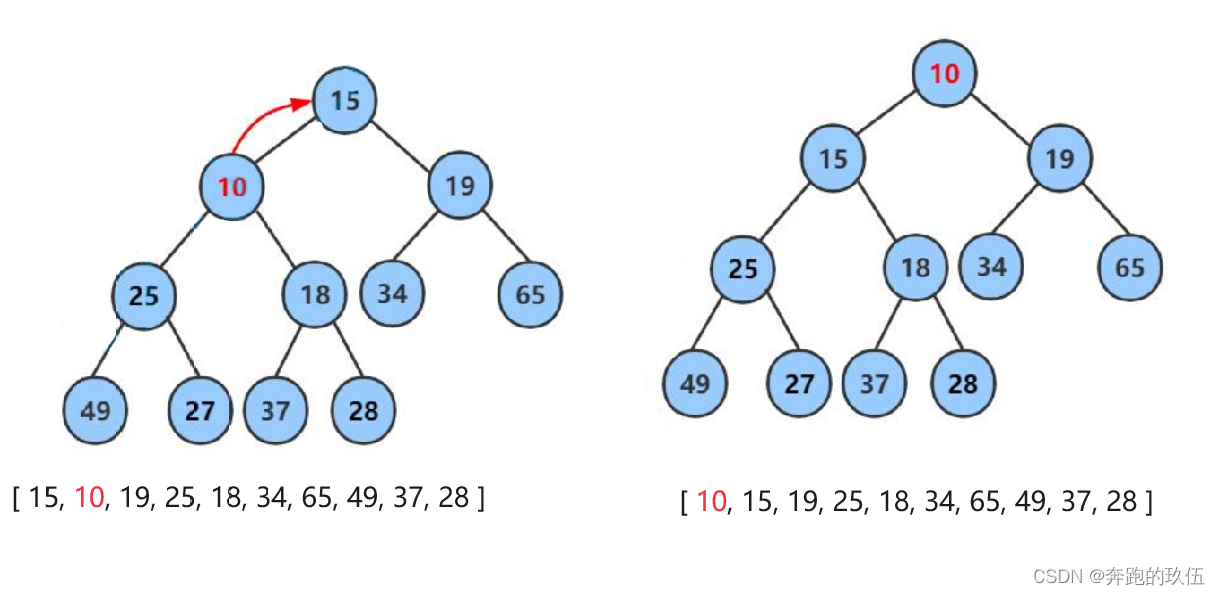
向上调整的过程 :将新插入的值与它的父亲相比,如果小则向上调整,调整完成后与新的父亲去比较,直到其值 >= 父亲的时候停止调整
void Swaps(HPDataType* a, HPDataType* b) {HPDataType temp;temp = *a;*a = *b;*b = temp;
}//向上调整(小堆)
//child是下标void AdjustUp(HPDataType* a, int child) {assert(a);int parent = (child - 1) / 2;//算父亲节点的下标//向下调整主要逻辑while (child > 0) //当调整至根节点时,已经调整至极限,不用在调整{//当父亲节点 > 孩子时,开始调整if (a[parent] > a[child]) {Swaps(&a[child],&a[parent]); //交换child = parent; //走到新的位置为新一轮的向下调整做准备parent = (child - 1) / 2; //算出新位置的父亲节点下标}//当父亲节点 < 孩子时,说明调整已经完毕,退出循环else{break;}}
}2.3堆向下调整算法
在堆排序或其他需要维护堆性质的场景中,当堆的某个节点不满足堆的性质(对于最大堆,父节点小于其子节点;对于最小堆,父节点大于其子节点)时,就需要通过向下调整来修复这个子树,使其重新成为堆
int array[] = {27,15,19,18,28,34,65,49,25,37};
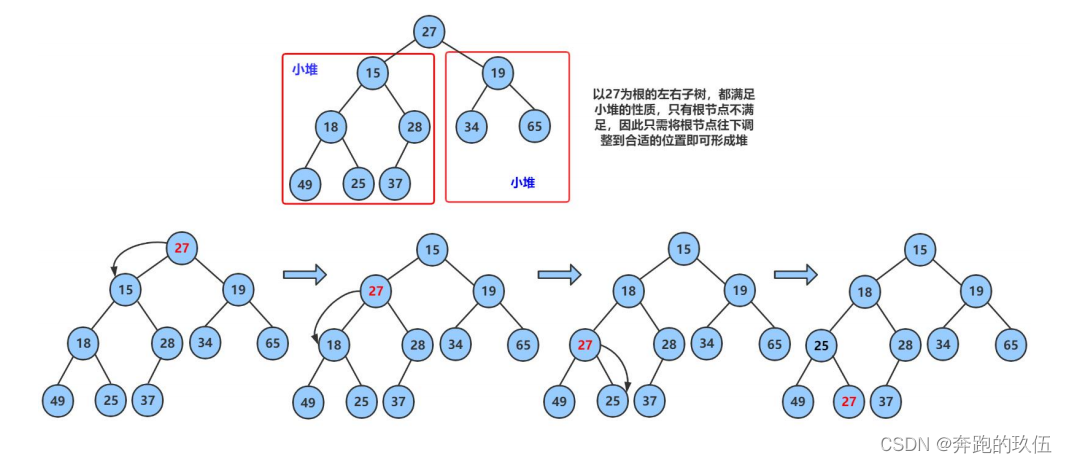
2.4堆的插入
堆的插入(HeapPush):通常通过将新元素添加到堆的末尾,并通过向上调整算法来维持堆的性质 (由于插入前的堆肯定是一个标准的堆,所以我们在将数据插入后执行一次向上调整算法,即可完成堆的插入)
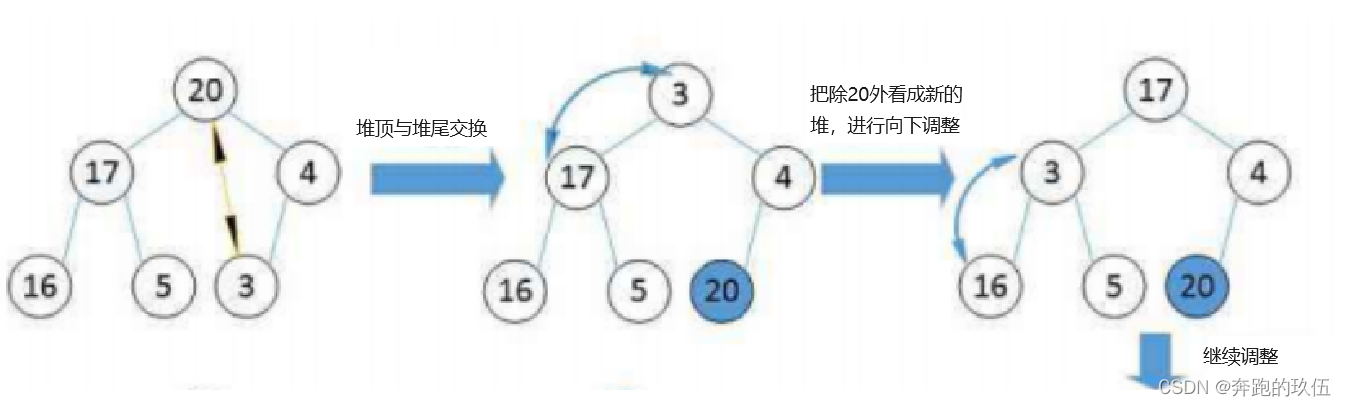
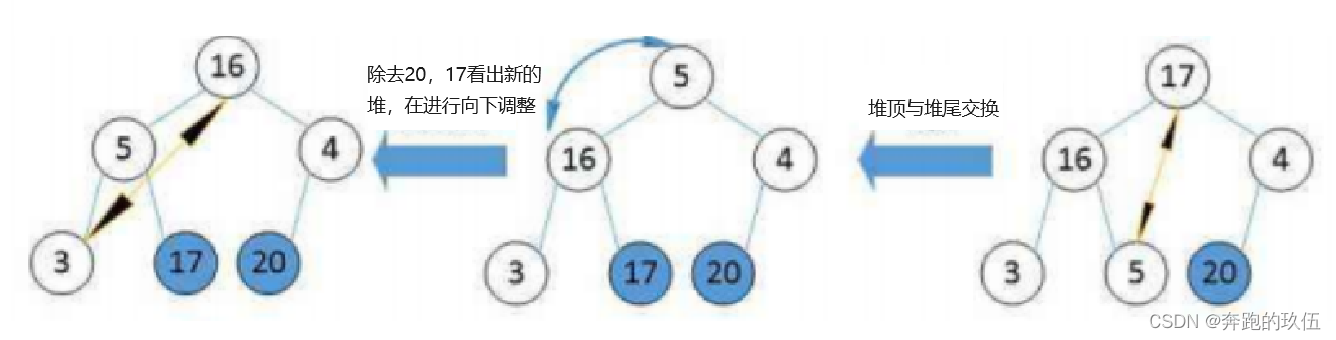
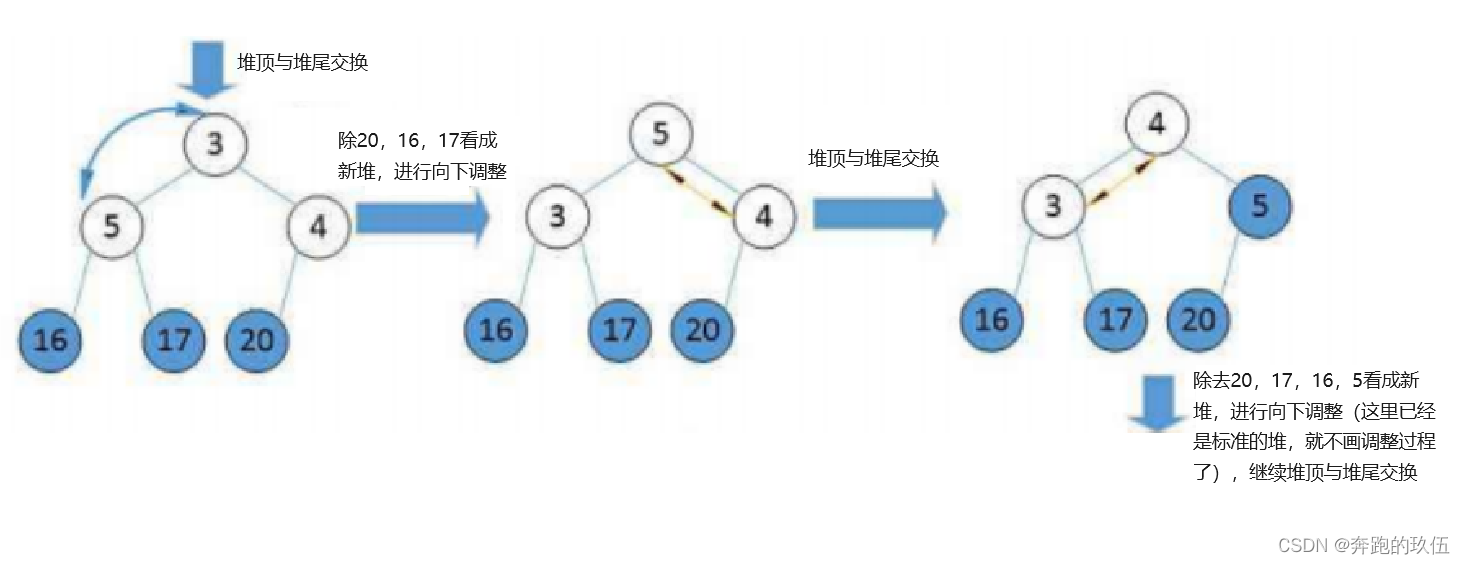
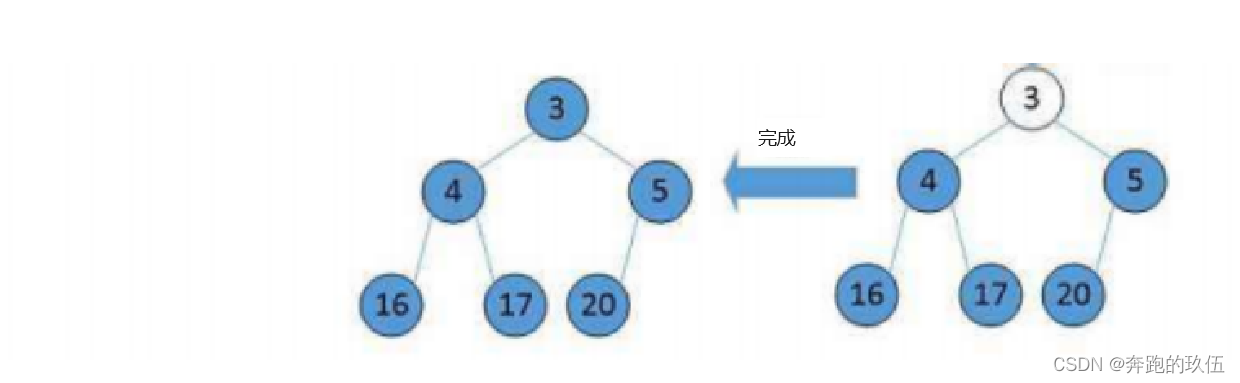
2.5堆的删除
删除元素(HeapPop):在最大堆或最小堆中,通常删除的是根节点(即最大或最小元素),并通过向下调整算法来维持堆的性质 (由于删除前的堆肯定是一个标准的堆即左右子树肯定也是标准的堆,所以我们在将数据删除后执行一次向下调整算法,即可完成堆的删除)
为什么要删除根节点?
- 相较于删除别的位置的节点,每次删除的根节点都是堆中最大或最小的数(大堆为最大,小堆为最小)、
- 从根节点开始删除并调整堆结构,在实现上相对简便。只需删除后算法向下调整即可
2.6堆的代码实现
Heap.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;//堆的初始化
void HeapInit(Heap* php);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);//向上调整
void AdjustUp(HPDataType* a, int child);
//向下调整
void AdjustDown(HPDataType* a, int n, int parent);Heap.c
//堆的初始化
void HeapInit(Heap* hp) {assert(hp);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}
// 堆的销毁
void HeapDestory(Heap* hp) {assert(hp);free(hp->_a);hp->_capacity = hp->_size = 0;}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x) {assert(hp);//扩容if (hp->_size == hp->_capacity){int newcapacity = hp->_capacity == 0 ? 2 : hp->_capacity * 2;HPDataType* newa = (HPDataType*)realloc(hp->_a, newcapacity * sizeof(HPDataType));if (newa == NULL){perror("realloc");return;}hp->_capacity = newcapacity;hp->_a = newa;}//插入数据hp->_a[hp->_size] = x;hp->_size++;//向上调整AdjustUp(hp->_a,hp->_size-1);}
void Swaps(HPDataType* a, HPDataType* b) {HPDataType temp;temp = *a;*a = *b;*b = temp;
}
//向上调整(小堆)
//child是数组的下标
void AdjustUp(HPDataType* a, int child) {assert(a);int parent = (child - 1) / 2;while (child > 0){if (a[parent] > a[child]){Swaps(&a[child],&a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
// 堆的删除
void HeapPop(Heap* hp) {assert(hp);assert(hp->_size);//删除顶部数据 ,先与末尾的交换,在向下调整Swaps(&hp->_a[0],&hp->_a[hp->_size-1]);//让数组首元素,与尾元素交换位置hp->_size--;AdjustDown(hp->_a, hp->_size, 0);}
//向下调整(小堆)
//n是数据数个数
void AdjustDown(HPDataType* a, int n, int parent) {assert(a);//假设法,默认两个孩子最小的是左孩子int child = parent * 2 + 1;//当没有左孩子的时候停止向下调整,拿新算的孩子位置去判断while (child < n){if (child + 1 < n && a[child + 1] < a[child])//挑最小的孩子换,且要注意有没有右孩子{child += 1;}if (a[child] < a[parent])//孩子比父亲小就往上换{Swaps(&a[child], &a[parent]);parent = child;//孩子变成父亲,与他的孩子比child = parent * 2 + 1;}else{break;}}}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp) {assert(hp);assert(hp->_size);return hp->_a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp) {assert(hp);return hp->_size;
}
// 堆的判空
int HeapEmpty(Heap* hp) {return hp->_size == 0;
}3堆的应用 — 堆排序
堆排序,我们肯定是运用堆这个数据结构来完成我们的堆排序
接下来我们将充分的了解堆排序的运作原理
不难看出
- 在每次交换时,堆顶最小的数都会沉到当前堆底
- 小堆在经历过N(数据个数)轮后就会得到一个升序的数组
- 大堆在经历过N(数据个数)轮后就会得到一个降序的数组
知道了堆排序的运转过程之后还有一个问题:使用者不可能说给你一个堆结构让你排序,肯定给的是一串无序且不是堆的数组给你排,这时侯我们就要考虑如何建堆了
3.1建堆
难道说建堆要用到上面写的堆结构,一个一个的去push吗?
其实不然,我们只需要使用向上调整算法或向下调整算法就可以完成建堆
向上调整建堆法
1.构建过程:
- 初始时,将数组的第一个元素视为堆的根节点(对于下标从0开始的数组,根节点的下标为0)
- 对于数组中剩余的元素(从下标1开始),将它们逐个视为“新插入”的元素,并执行向上调整操作
- 在向上调整过程中,对于当前元素,首先计算其父节点的下标(parent = (child - 1) / 2)。然后,比较当前元素与其父节点的值
- 如果当前元素的值大于其父节点的值(对于大根堆),则交换它们的位置。然后,将当前元素设置为新交换位置的父节点,并重复上述步骤,直到当前元素的值不大于其父节点的值或已经到达根节点
- 通过重复上述步骤,直到所有元素都被处理过,最终得到的数组将满足堆的性质
2.时间复杂度:
- 向上调整建堆法的时间复杂度为O(N * logN),其中N是数组中的元素数量
void Swaps(int* a, int* b) {int temp;temp = *a;*a = *b;*b = temp; }//向上调整(小堆) void AdjustUp(int* a, int child) {assert(a);int parent = (child - 1) / 2;while (child > 0){if (a[parent] > a[child]){Swaps(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}} }//堆排序 void HeapSort(int* a, int n) {//创建堆,向上调整建堆for (int i = 1; i < n; i++) {AdjustUp(a,i);}}
向下调整建堆法
向下调整(Adjust Down)是指从给定的非叶子节点开始,通过与其子节点比较并交换位(如果需要)来确保堆的性质
1.构建过程
- 确定开始位置:
- 对于长度为n的数组,由于堆是完全二叉树,所以最后一个非叶子节点的下标为
(n-1-1)/2(整数除法)- 从这个下标开始,向前遍历所有非叶子节点
- 执行向下调整
- 遍历结束:
- 当所有非叶子节点都经过向下调整后,整个数组就形成了一个堆
2.时间复杂度
向下调整建堆法的时间复杂度为O(N),其中N是数组中的元素数量
void Swaps(int* a, int* b) {int temp;temp = *a;*a = *b;*b = temp; } //向上调整(小堆) void AdjustUp(int* a, int child) {assert(a);int parent = (child - 1) / 2;while (child > 0){if (a[parent] > a[child]){Swaps(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}} }//堆排序 void HeapSort(int* a, int n) {//创建堆,向下调整建堆int parent = (n - 1 - 1) / 2; //找到最后一个非叶子节点for (parent; parent >= 0; parent--){AdjustDown(a, n, parent);}}
3.2 利用堆删除思想来进行排序
void Swaps(int* a, int* b) {int temp;temp = *a;*a = *b;*b = temp;
}//向上调整(小堆)
void AdjustUp(int* a, int child) {assert(a);int parent = (child - 1) / 2;while (child > 0){if (a[parent] > a[child]){Swaps(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}//向下调整(小堆)
void AdjustDown(int* a, int n, int parent) {assert(a);int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child += 1;}if (a[child] < a[parent]){Swaps(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}//堆排序
void HeapSort(int* a, int n) {创建堆,向上调整建堆//for (int i = 1; i < n; i++)//{// AdjustUp(a, i);//}//创建堆,向下调整建堆int parent = (n - 1 - 1) / 2;for (parent; parent >= 0; parent--){AdjustDown(a, n, parent);}//小堆,可以排降序while (n){Swaps(&a[0], &a[n - 1]);//交换完成把除了最后一个数据之外的数组看成一个新的堆,开始向下交换,形成新的小堆n--;AdjustDown(a, n, 0);}}4堆的应用 — Top-K问题
- 前k个最大的元素,则建小堆
- 前k个最小的元素,则建大堆
void Swaps(int* a, int* b) {int temp;temp = *a;*a = *b;*b = temp;
}//向下调整(小堆)大的下去
//n是数据数个数
void AdjustDown(HPDataType* a, int n, int parent) {assert(a);int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child += 1;}if (a[child] < a[parent]){Swaps(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}
void CreateNDate()
{// 造数据int n = 10000;srand((unsigned int)time(NULL));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (size_t i = 0; i < n; ++i){int x = rand() % 1000000;fprintf(fin, "%d\n", x);}fclose(fin);
}void PrintTopK(int k) {//找出前K个最大的数//打开文件FILE* p = fopen("data.txt", "r");if (p == NULL){perror("fopen error");return;}//构建一个小堆int x = 0;int arr[10] = { 0 };for (int i = k; i < 10; i++){fscanf(p,"%d", &x);arr[i] = x;}//创建堆,向下调整建堆,F(N)int parent = (k - 1 - 1) / 2;for (parent; parent >= 0; parent--){AdjustDown(arr, k, parent);//这里的n数组的位置,里面的child会算出超过数组的位置,这样会停下来}//在将后面的数字依次对比小堆顶部,比它大就向下调整while (fscanf(p, "%d", &x) > 0){if (arr[0] < x){arr[0] = x;AdjustDown(arr, k, 0);}}for (int i = 0; i < k; i++){printf("%d\n", arr[i]);}
}相关文章:
数据结构 —— 堆
1.堆的概念及结构 堆是一种特殊的树形数据结构,称为“二叉堆”(binary heap) 看它的名字也可以看出堆与二叉树有关系:其实堆就是一种特殊的二叉树 堆的性质: 堆中某个结点的值总是不大于或不小于其父结点的值&…...

【运维】如何更换Ubuntu默认的Python版本,update-alternatives如何使用
update-alternatives 是一个在 Debian 及其衍生发行版中(包括 Ubuntu)用于管理系统中可替代项的命令。它可以用于在系统中设置默认的软件版本,例如在不同版本的软件之间进行切换,比如不同的 Python 版本。 要在 Ubuntu 中使用 up…...
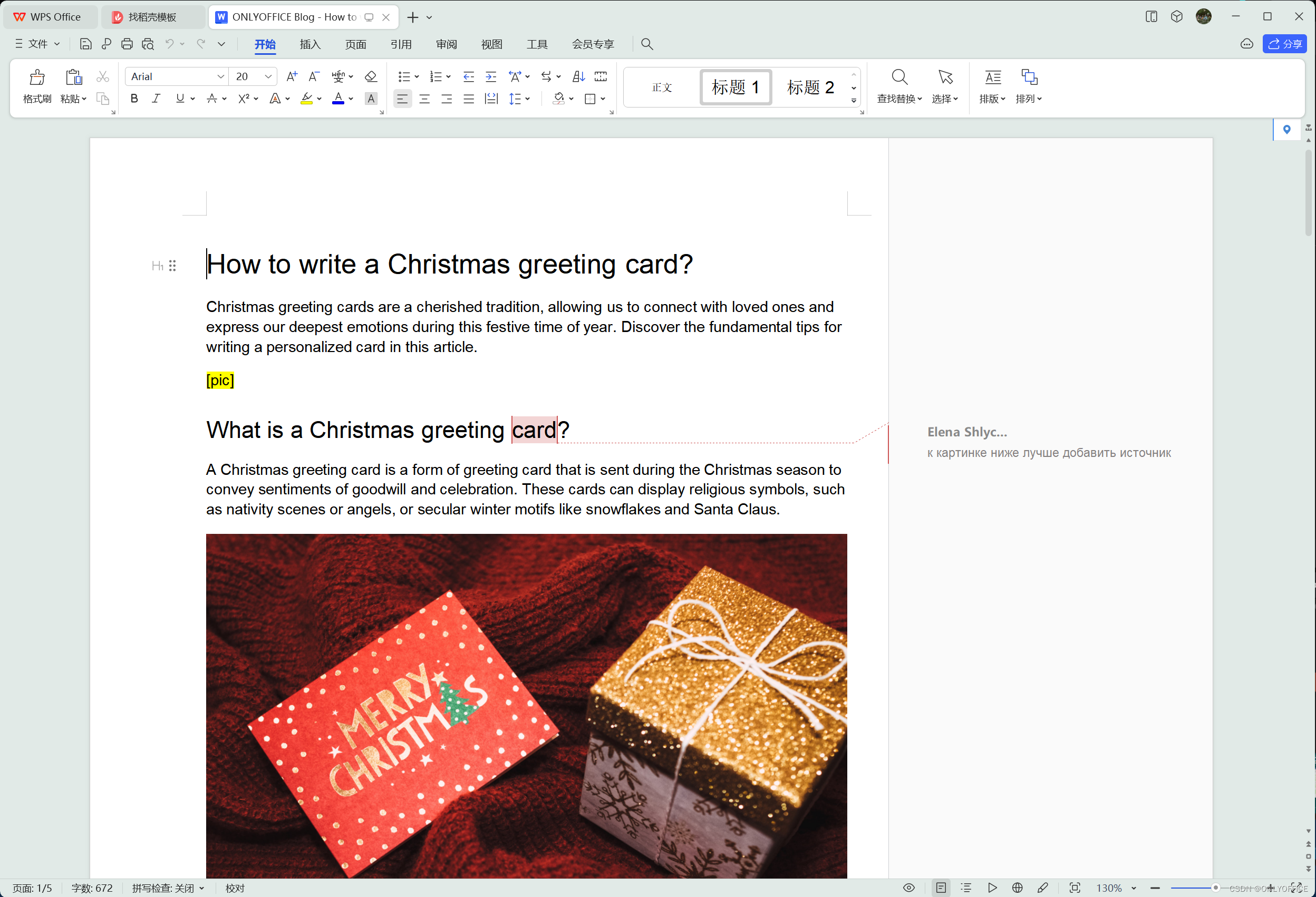
2024 年适用于 Linux 的 5 个微软 Word 替代品
对于那些最近由于隐私问题或其他原因而转向 Linux 的用户来说,可能很难替换他们最喜欢的、不在 Linux 操作系统上运行的应用程序。 寻找流行程序的合适替代品可能会成为一项挑战,而且并不是每个人都准备好花费大量时间来尝试弄清楚什么可以与他们在 Win…...

大模型日报2024-06-12
大模型日报 2024-06-12 大模型资讯 NVIDIA发布GB200 Grace Blackwell AI超级芯片 摘要: NVIDIA近日宣布推出GB200 Grace Blackwell超级芯片和Blackwell B200 GPU,这些新技术将推动人工智能领域的发展。 阿布扎比TII发布下一代Falcon语言模型 摘要: 阿布扎比的技术创…...
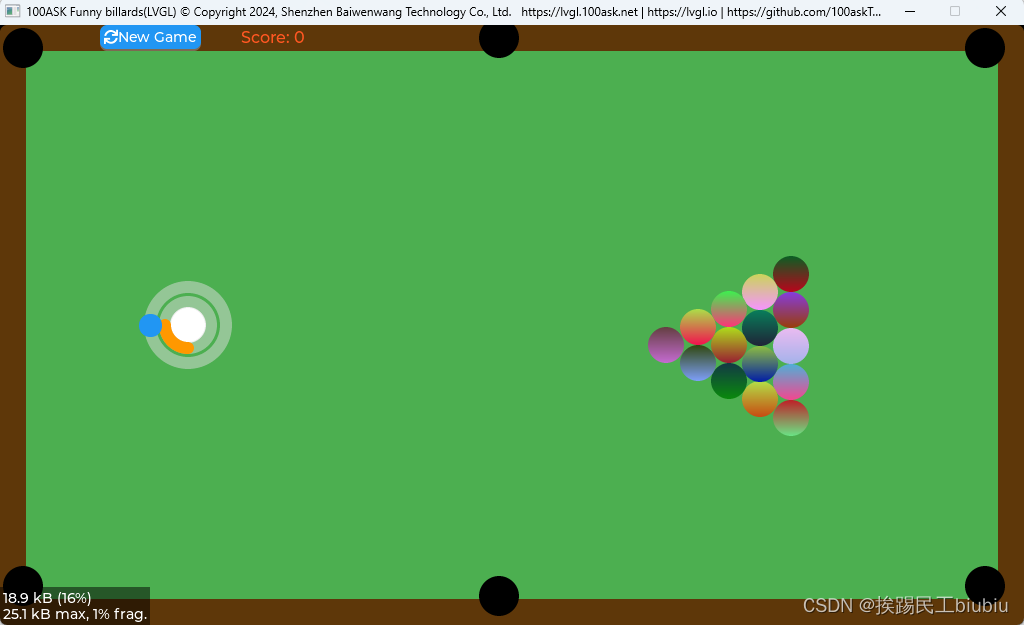
LVGL欢乐桌球游戏(LVGL+2D物理引擎学习案例)
LVGL欢乐桌球游戏(LVGL2D物理引擎学习案例) 视频效果: https://www.bilibili.com/video/BV1if421X7DL...
国产数字证书大品牌——JoySSL
一、品牌介绍 网盾安全旗下品牌JoySSL是专业的https安全方案服务商,业务涉及网络安全技术服务、安全防护系统集成、数据安全软件开发等。网盾安全以网络安全为己任,携手GlobalSign、DigiCert 、Sectigo等全球数家权威知名SSL证书厂商,加速ht…...

Codeforces Global Round 26 D. “a“ String Problem 【Z函数】
D. “a” String Problem 题意 给定一个字符串 s s s,要求把 s s s 拆分成若干段,满足以下要求: 拆分出来的每一个子段,要么是子串 t t t,要么是字符 a a a子串 t t t 至少出现一次 t ≠ " a " t \ne…...
)
Next.js 加载页面及流式渲染(Streaming)
Next.js 加载页面及流式渲染(Streaming) 在现代的 Web 应用开发中,用户体验是至关重要的。快速响应的页面加载和流畅的用户界面可以显著提升用户的满意度。而加载页面(Loading Page)和流式渲染(Streaming&…...

形如SyntaxError: EOL while scanning string literal,以红色波浪线形式在Pycharm下出现
背景: 新手在学习Python时可能会出现如下图所示的报错 下面分情况教大家如何解决 视频教程【推荐】: 形如SyntaxError: EOL while scanning string literal,以红色波浪线形式在Pycharm下出现 过程: 问题概述: 简单…...
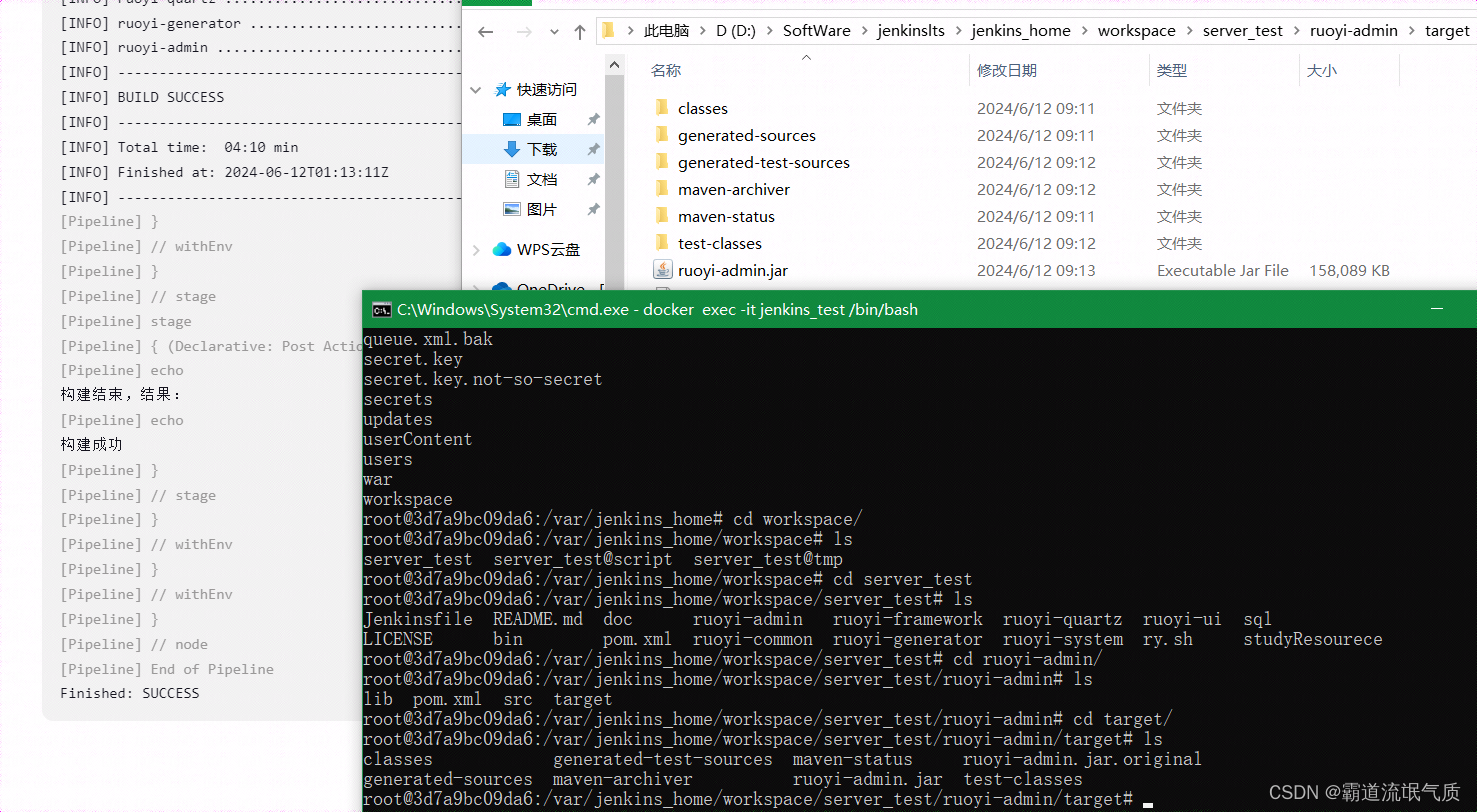
DockerCompose+Jenkins+Pipeline流水线打包SpringBoot项目(解压安装配置JDK、Maven等)入门
场景 DockerCompose中部署Jenkins(Docker Desktop在windows上数据卷映射): DockerCompose中部署Jenkins(Docker Desktop在windows上数据卷映射)-CSDN博客 DockerJenkinsGiteeMaven项目配置jdk、maven、gitee等拉取代…...

Web前端开发个人技能全面剖析:四维度深度理解,五能力实战展现,六要素构建优势,七步骤持续精进
Web前端开发个人技能全面剖析:四维度深度理解,五能力实战展现,六要素构建优势,七步骤持续精进 在数字化浪潮的推动下,Web前端开发成为了互联网行业中的热门岗位,对个人的技能要求也越来越高。本文将从四个…...
)
如何让 uboot启动时自动执行指令?(执行“mtdparts default”命令)
让uboot启动时自动设置分区(执行“mtdparts default”命令),在uboot进入main_loop()死循环之前添加执行命令代码 run_command("mtdparts default", 0); #define MTDIDS_DEFAULT "nand0mini2440-nand" #define MTD…...

Java的集合框架总结
Map接口和Collection接口是所有集合框架的父接口: Collection接口的子接口包括:Set接口和List接口 Map接口的实现类主要有:HashMap、TreeMap、Hashtable、ConcurrentHashMap以及Properties等 Set接口的实现类主要有:HashSet、Tr…...

基于DenseNet网络实现Cifar-10数据集分类
目录 1.作者介绍2.Cifar-10数据集介绍3.Densenet网络模型3.1网络背景3.2网络结构3.2.1Dense Block3.2.2Bottleneck层3.2.3Transition层3.2.4压缩 4.代码实现4.1数据加载4.2建立 DenseNet 网络模型4.3模型训练4.4训练代码4.5测试代码 参考链接 1.作者介绍 吴思雨,女…...

我的“工具”库
#使用到的工具# { 网页版的VScode: www.vscode.dev} {网页版JSON文件编辑器: JSON Editor Online: edit JSON, format JSON, query JSON } {网页版XML文件编辑器: Best Online XML Viewer, XML Formatter, XML Editor, Analyser, Be…...

Pytorch常用函数用法归纳:Tensor张量之间的计算
1.torch.add() (1)函数原型: torch.add(input, other, alpha, out) (2)参数说明: 参数名称参数类型参数说明inputtorch.Tensor表示参与运算的第一个输入Tensor张量othertorch.Tensor或者Number表示参与运算的第二个输入Tensor张量或标量alphaNumber, optional一个可选的缩放…...

小公司要求真高
大家好,我是白露啊。 最近看到一个爽文帖,标题就是——“小公司要求真高”。 事情是这样的,一家的小公司在拿到简历之后,HR直接对楼主说:“你不合适,简历不行。” 言外之意就是嫌弃简历单薄,看…...

进阶篇02——索引
概述 结构 B树索引 在这里推荐一个可以将个各种数据结构可视化的网站:数据结构可视化 哈希索引 相关的一个面试题 分类 聚集索引和二级索引(非聚集索引) 思考题:索引思考题 创建索引语法 如果一个索引关联多个字段ÿ…...

三:SpringBoot的helloworld和使用Springboot的优点以及快速创建Springboot应用
三:SpringBoot的helloworld和使用Springboot的优点以及快速创建Springboot应用 一:HelloWorld [我们创建的是maven项目或者直接创建一个Spring] 1.1:创建一个maven 项目(1】:需要自己手动写一个SpringBoot 的启动类同…...

网络仿真方法综述
目录 1. 引言 2.仿真器介绍 2.1 NS-2 2.2 NS-3 2.3 OPNET 2.4 GNS3 3.仿真对比 4.结论 参考文献 1. 引言 网络仿真是指使用计算机模拟网络系统的行为和性能的过程。在网络仿真中,可以建立一个虚拟的网络环境,并通过模拟各种网络设备、协议和应用程…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...