深层网络:层数多真的更好吗?
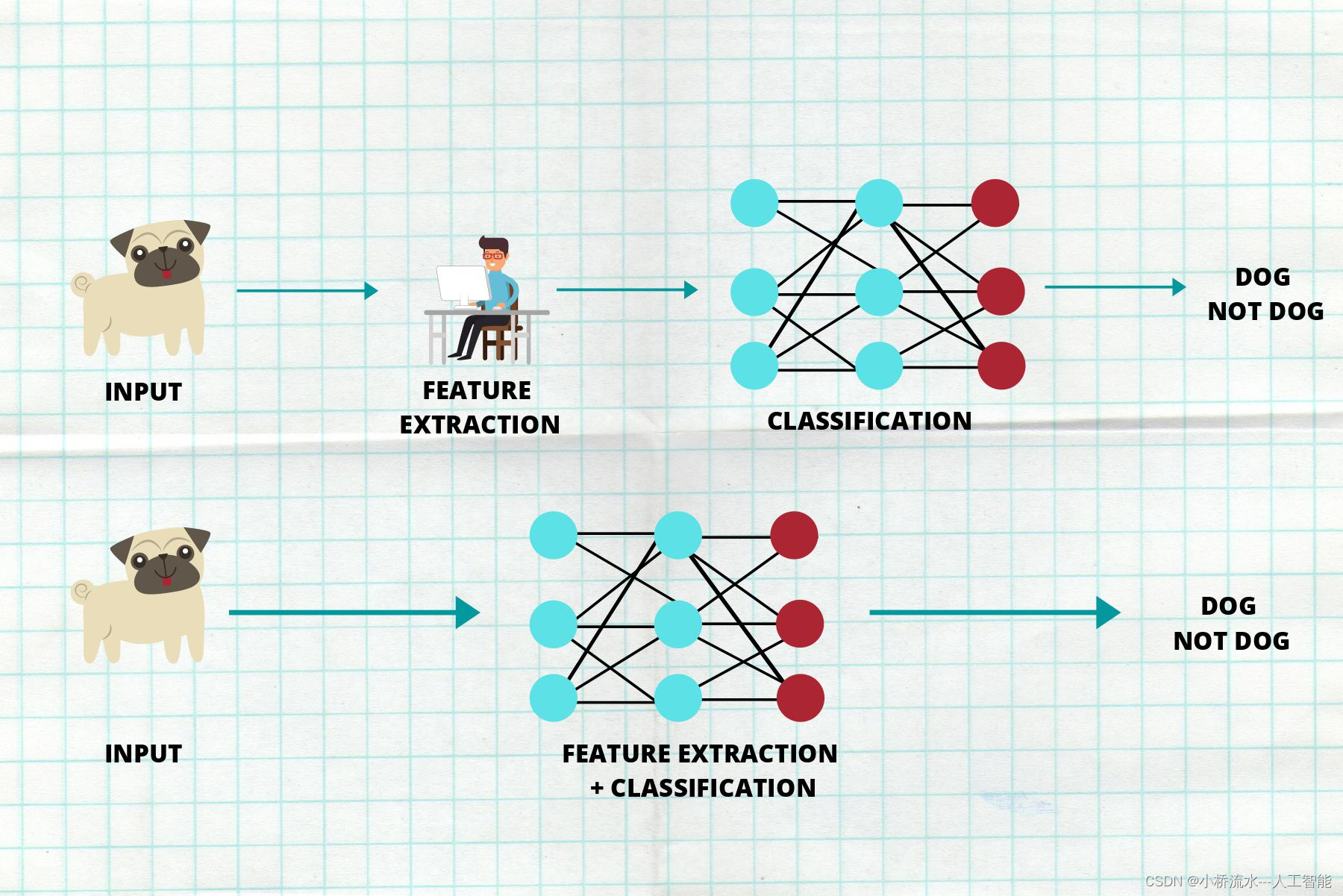
深层网络:层数多真的更好吗?
在深度学习的世界里,"深度"始终是一个热门话题。随着技术的发展,我们有了越来越多的方法来构建更深的神经网络,这似乎暗示着“层数越多,效果越好”。然而,这种观点是否总是成立?本文将探讨深度学习中层数与模型性能的关系,以及深层网络在实际应用中的优势与限制。
一、深层网络的优势
1. 增加模型的表达能力
理论上,随着层数的增加,神经网络的表达能力也会增强。深层网络能够学习更复杂的特征和模式,这在复杂任务如图像识别、自然语言处理等领域尤其明显。例如,卷积神经网络(CNN)通过增加层数,能够从简单的边缘信息逐渐抽象到复杂的对象特征。
2. 更好的特征自动学习能力
深层网络通过多层非线性变换,可以自动学习数据中的高级抽象特征,而无需手动设计特征。这种层次化的特征学习方式是深度学习成功的关键因素之一。
二、深层网络面临的挑战
尽管深层网络具有显著的优势,但在实际应用中也面临一些不容忽视的挑战:
1. 过拟合问题
虽然有各种防止过拟合的技术(如Dropout、正则化等),深层网络由于参数众多,依然容易发生过拟合,尤其是在数据量有限的情况下。
2. 梯度消失和梯度爆炸
深层网络可能会遇到梯度消失或梯度爆炸的问题,这会导致网络难以训练。虽然有ReLU激活函数、批归一化(Batch Normalization)等方法缓解这一问题,但层数过多时仍可能遇到困难。
3. 计算资源和训练时间
随着模型层数的增加,所需的计算资源和训练时间也会显著增加。这不仅提高了训练成本,也限制了模型在资源受限的环境中的应用。
三、层数多真的更好吗?
答案是:不一定。模型的最佳层数取决于多种因素,包括但不限于任务的复杂度、可用数据的量和质、计算资源的限制等。深层网络虽好,但并非适合所有情况。
1. 任务的复杂性
对于一些简单的任务,使用较浅的网络就足够了,而且可能更有效。对于复杂的任务(如大规模图像或视频处理),则可能需要更深的网络来捕捉复杂的特征。
2. 数据的可用性
拥有大量高质量数据时,深层网络能够展现其优势。但在数据有限的情况下,过深的网络易过拟合,效果反而不佳。
3. 实际应用需求
在实际应用中,除了模型的准确性外,还需要考虑模型的推理时间和运行成本。在一些对实时性要求高的应用中,过深的网络可能因计算延迟而不适用。
四、结论
在设计深度学习模型时,合理选择网络的深度是至关重要的。虽然增加层数可以提升模型的学习能力和表达能力,但同时也带来了过拟合、梯度问题和计算成本的增加。因此,开发者需要根据具体任务的需求、数据的特点以及可用资源来权衡模型的深度和复杂度。正确的做法是通过实验来确定模型的最佳深度,确保模型既能捕获足够的特征,又能维持良好的泛化能力和实用性。
相关文章:

深层网络:层数多真的更好吗?
深层网络:层数多真的更好吗? 在深度学习的世界里,"深度"始终是一个热门话题。随着技术的发展,我们有了越来越多的方法来构建更深的神经网络,这似乎暗示着“层数越多,效果越好”。然而࿰…...
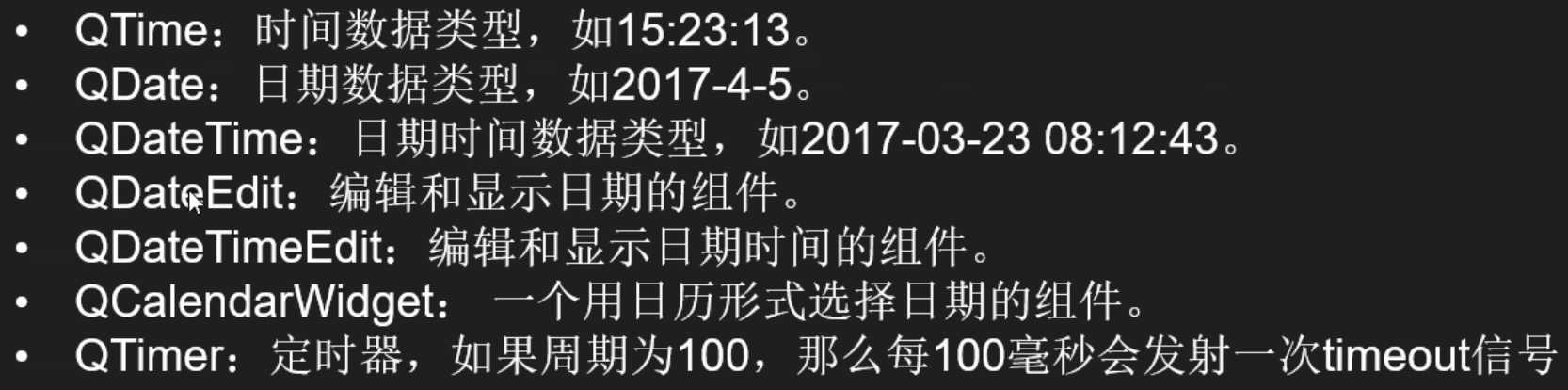
【QT5】<知识点> QT常用知识(更新中)
目录 一、更改文本颜色和格式 二、QT容器类 三、字符串与整数、浮点数之间的转换 四、QString常用功能 五、SpinBox的属性介绍 六、滑动、滚动、进度条和表盘LCD 七、时间、日期、定时器 一、更改文本颜色和格式 动态设置字体粗体:QFont对象的setBold方法动态…...

如何将AndroidStudio和IDEA的包名改为分层级目录
新版UIAndroidStudio 1、点击项目目录右上角如图所示的三个点点。 2、然后依次取消Hide empty middle package ,Flatten package的勾选 3、注意:一定要先取消hide的勾选,不然目录不会完全分级(做错了可以反过来重新设置&#x…...
北交字节联合提出ClassDiffusion: 使用显式类别引导的一致性个性化生成。
在个性化生成领域, 微调可能会引起过拟合导致模型无法生成与提示词一致的结果。针对这个问题,北交&字节联合提出ClassDiffusion,来提升个性化生成的一致性。 通过两个重要观察及理论分析提出了新的观点:一致性的损失是个性化概念语义偏移导致的, 还…...

37、matlab矩阵运算
1、前言 矩阵运算是指对矩阵的各种操作和运算,包括矩阵加法、矩阵减法、矩阵乘法、矩阵转置、求逆矩阵等。以下是常见的矩阵运算: 矩阵加法:对应位置的元素相加,要求加数和被加数的维度相同。 A B | a11 b11 | | a12 b12 | | …...

用软件实现的硬件——虚拟机
通过软件实现CPU和内存等硬件所具有的功能,并在计算机中运行循环的计算机技术称为虚拟机。使用虚拟机,就可以在一台计算机中运行多个循环出来的计算机。 近几年的计算机,除了硬件具有较高的性能外,CPU的性能也有了提升。因此&…...
[Shell编程学习路线]--shell中重定向和管道符(详细介绍)
🏡作者主页:点击! 🛠️Shell编程专栏:点击! ⏰️创作时间:2024年6月12日10点50分 🀄️文章质量:93分 ——前言—— 在Shell编程中,重定向和管道符是两个…...

Linux命令详解(1)
在Linux操作系统中,命令行界面(CLI)是一个强大的工具,它允许用户通过键入命令来与系统交互。无论是系统管理员还是普通用户,掌握一些基本的Linux命令都是非常重要的。在本文中,我们将探讨一些常用的Linux命…...

网工内推 | 深信服、中软国际技术支持工程师,最高13k*13薪
01 深信服 🔷招聘岗位:远程技术支持工程师 🔷任职要求: 一、专业能力和行业经验: ①具备友商同岗位工作经验1.5年以上,具备良好的分析和判断能力,有独立问题处理思路,具备常见协…...

实现卡片的展开缩放动画
原理,外层包裹一个元素,子元素分别是展开和收起的元素,然后对展开的元素添加动画,动画内容是随时间变化,将卡片的transform:rotateX属性进行调整,因为改变的是子元素的旋转,父元素高…...

实验:贪心算法
实验二:贪心算法 【实验目的】 应用贪心算法求解活动安排问题。 【实验性质】 验证性实验。 【实验要求】 活动安排问题是可以用贪心算法有效求解的很好的例子。 问题:有n个活动的集合A{1,2,…,n},其中每个活动都要求使用同一资源&…...

Python学习笔记12 -- 有关布尔值的详细说明
一、布尔表达式 最终值为true 或者false 二、常见形式: 1、常量:true false 2、比较运算: and ! 3、复合运算: and and or 4、其他 例:检测闰年: def specialYearMine(year):if (year%4 …...

SQL-窗口函数合集
目录 1.窗口函数简介2.窗口的定义3.相关题目示例3.1 PERCENT_RANK()2346 以百分比计算排名 3.2 FIRST_VALUE()/LAST_VALUE()/NTH_VALUE()2388 将表中的空值更改为前一个值 1.窗口函数简介 MySQL 开窗函数(Window Functions)是 MySQL 8.0 版本引入的一个…...

2024 全球软件研发技术大会官宣,50+专家共话软件智能新范式!
2024年的全球软件研发技术大会(SDCon)由CSDN和高端IT咨询与教育平台Boolan联合主办,将于7月4日至5日在北京威斯汀酒店举行。本次大会的主题为“大模型驱动软件智能化新范式”,旨在探讨大模型和开源技术的发展如何引领全球软件研发…...
opencv快速安装以及各种查看版本命令
安装opencv并查看其版本,直接通过一个可执行文件实现。 #!/bin/bashwget https://codeload.github.com/opencv/opencv/zip/3.4 -O opencv-3.4.zip && unzip opencv-3.4.zip && cd opencv-3.4 && \mkdir build && cd build &&a…...
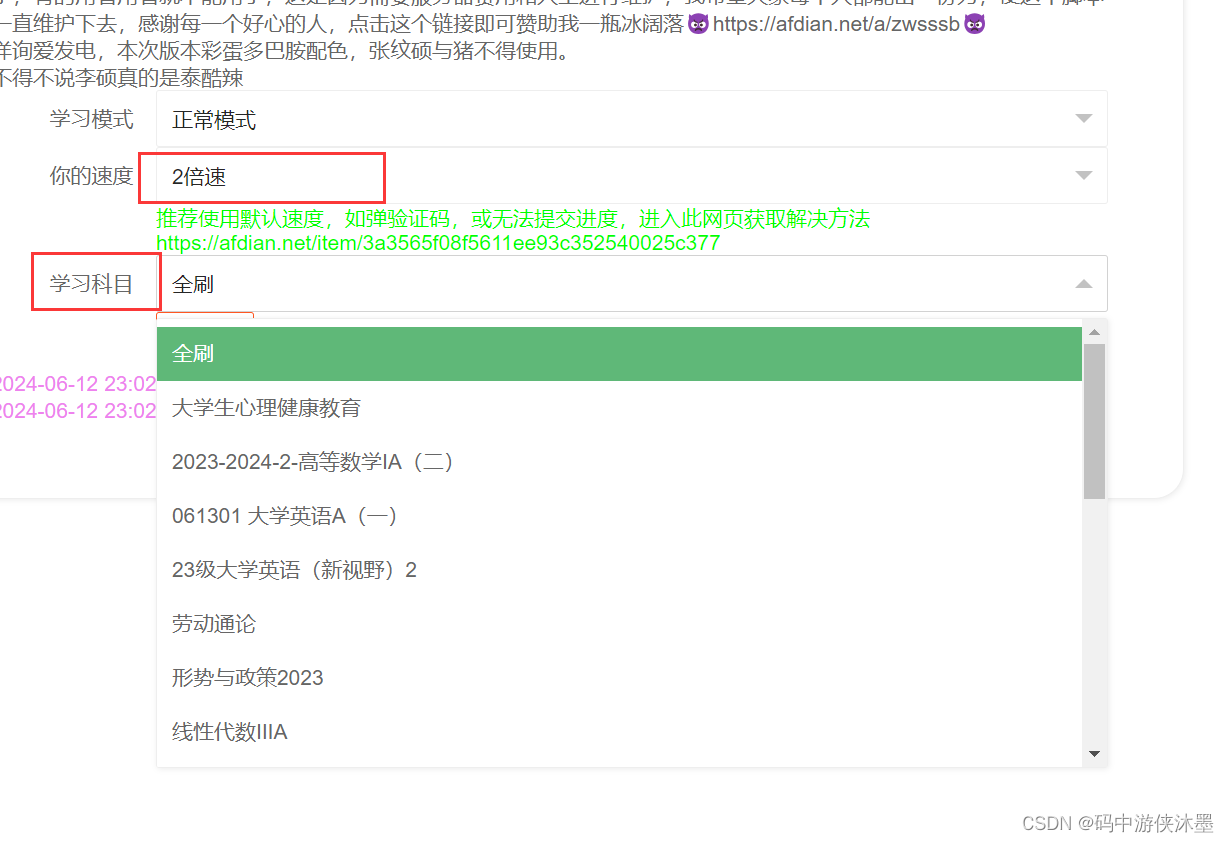
免费学习通刷课(免费高分)Pro版
文章目录 概要整体架构流程小结 概要 关于上一版的免费高分的学习通刷课,有很多人觉得还得登录太复杂了,然后我又发现了个神脚本,操作简单,可以后台挂着,但是还是建议调整速度到2倍速,然后找到你该刷的课&…...

线性数据结构-队列
队列(Queue)是一种先进先出(First In First Out, FIFO)的数据结构,它按照元素进入的顺序来处理元素。队列的基本操作包括: enqueue:在队列的末尾添加一个元素。dequeue:移除队列的第…...

python脚本将视频抽帧为图像数据集
AI应用开发相关目录 本专栏包括AI应用开发相关内容分享,包括不限于AI算法部署实施细节、AI应用后端分析服务相关概念及开发技巧、AI应用后端应用服务相关概念及开发技巧、AI应用前端实现路径及开发技巧 适用于具备一定算法及Python使用基础的人群 AI应用开发流程概…...

Xmind导入纯文本TXT方法
最近有很多同事咨询我如何在xmind直接导入纯文本txt笔记或者思维导图呢? 解决办法如下: 1.先打开xmind随便打开一个思维导图-文件-导出-marldown 2.选中导出的markdown文件。右键-打开方式-苹果系统选择文本编辑,Win系统选择记事本 3.按照图示…...

深度学习在老年痴呆检测中的应用:数据集综述
深度学习在老年痴呆检测中的应用:数据集综述 引言 老年痴呆(Alzheimer’s Disease, AD)是一种神经退行性疾病,主要影响老年人,导致记忆力、认知能力和行为的逐步衰退。早期检测和诊断对于延缓疾病进展、提高患者生活质量至关重要。近年来,深度学习技术在医学影像分析和…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
