mxnet版本与numpy,requests等都不兼容问题
简介
跟着李沐学AI时遇到的mxnet环境问题。
问题
使用pip install mxnet时会重新安装相匹配的numpy和requests,而这新安装的这两个版本不满足d2l所需的版本。
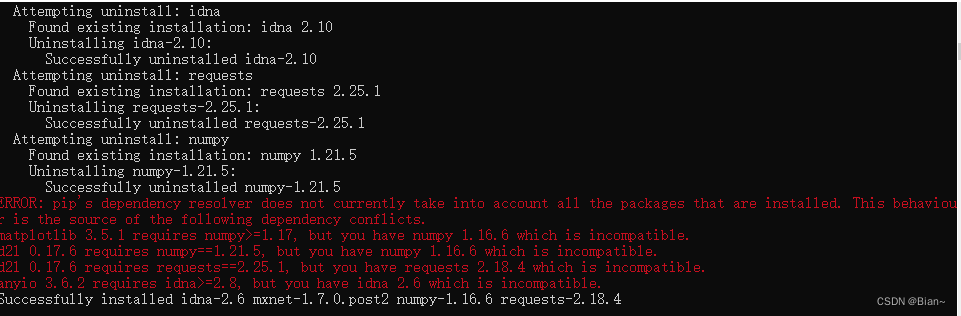
然后报错:
ERROR: pip's dependency resolver does not currently take into account all the packages that are installed. This behaviour is the source of the following dependency conflicts.
matplotlib 3.5.1 requires numpy>=1.17, but you have numpy 1.16.6 which is incompatible.
d2l 0.17.6 requires numpy==1.21.5, but you have numpy 1.16.6 which is incompatible.
d2l 0.17.6 requires requests==2.25.1, but you have requests 2.18.4 which is incompatible.
anyio 3.6.2 requires idna>=2.8, but you have idna 2.6 which is incompatible.
尝试
试图下载最新版本的mxnet,失败!

显示支持的版本最高只到1.7.0
解决
遍寻csdn无果后,回到d2l的安装那一节,终于成功解决。
- 步骤
- 首先,查看已安装的CUDA版本
nvcc --version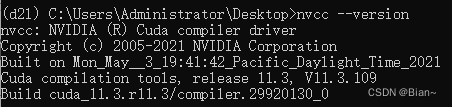
我的版本是11.3- 安装命令:
可以根据CUDA版本更改如上mxnet-cu101的最后一位数字, 例如:CUDA 10.0是cu100, CUDA 9.0是cu90。pip install mxnet-cu101==1.7.0
我的是CUDA 11.3,所以我的命令是:pip install mxnet-cu113==1.7.0
发现我的库里只有1.0.0版本,所以直接下载1.0.0版本尝试一下:

- 下载成功,回到jupyter notebook尝试运行。运行成功!
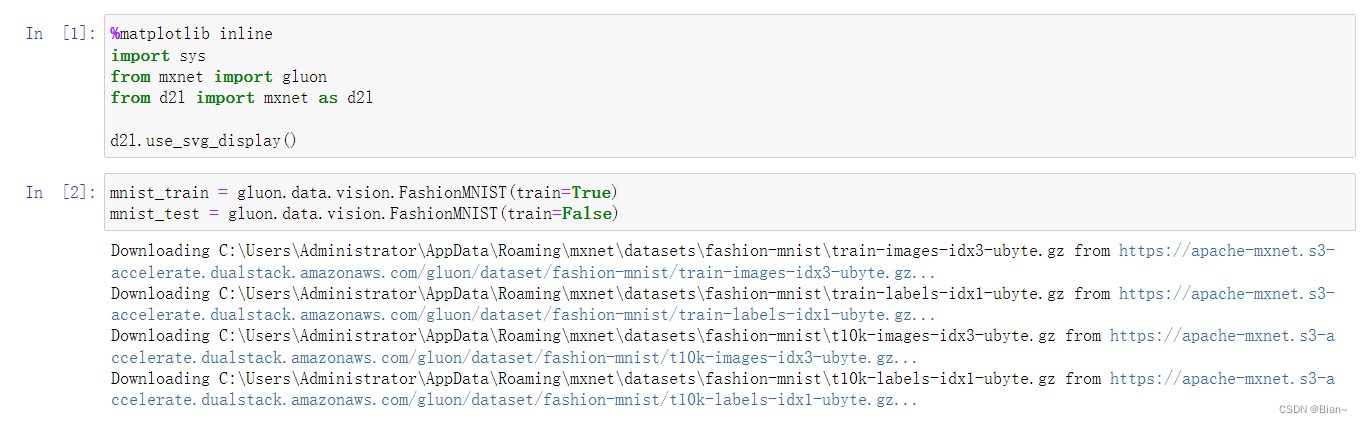
成功解决,撒花!!!!
过后反思
最后发现其实用不上mxnet,忘了点pytorch代码,被自己蠢哭了,呜呜呜~~~
相关文章:

mxnet版本与numpy,requests等都不兼容问题
简介 跟着李沐学AI时遇到的mxnet环境问题。 问题 使用pip install mxnet时会重新安装相匹配的numpy和requests,而这新安装的这两个版本不满足d2l所需的版本。 然后报错: ERROR: pips dependency resolver does not currently take into account all …...

逆向分析——壳
你脑海中的壳是什么 壳在自然界是动物的保护壳,软件同样有保护壳,为了防止破解 也许大海给贝壳下的定义是珍珠,也许时间给煤炭下的定义是钻石 ——沙与沫 壳的由来 在DOS时代,壳一般指的是磁盘加密软件中的一段加密程序 后来发展…...
为 Argo CD 应用程序指定多个来源
在 Argo CD 2.6 中引入多源功能之前,Argo CD 仅限于管理来自 单个 Git 或 Helm 存储库 的应用程序。用户必须将每个应用程序作为 Argo CD 中的单个实体进行管理,即使资源存储在多个存储库中也是如此。借助多源功能,现在可以创建一个 Argo CD 应用程序,指定存储在多个存储库…...

verilog specify语法
specify block用来描述从源点(source:input/inout port)到终点(destination:output/inout port)的路径延时(path delay),由specify开始,到endspecify结束&…...

CMake编译学习笔记
CMake学习笔记CMake编译概述CMake学习资源CMake编译项目架构cmake指令CMakeList基础准则CMakeList编写项目构建cmake_minimum_required() 和 project()set()find_package()add_executable()aux_source_directory()连接库文件include_directories()和target_include_directories…...
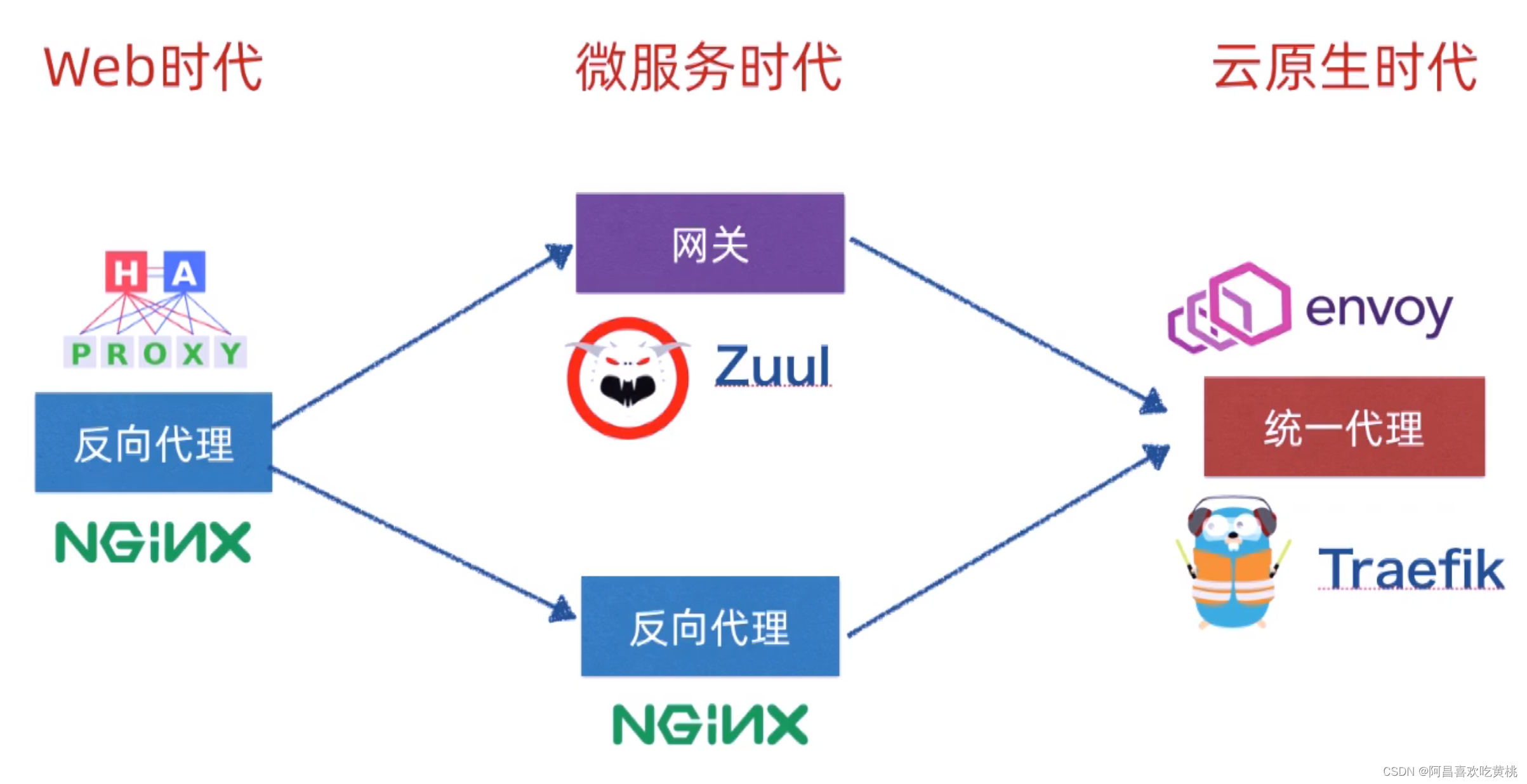
Day913.反向代理和网关是什么关系 -SpringBoot与K8s云原生微服务实践
反向代理和网关是什么关系 Hi,我是阿昌,今天学习记录的是关于反向代理和网关是什么关系的内容。 一、反向代理 反向代理 是一种网络技术,用于将客户端的请求转发到一个或多个服务器上,并将响应返回给客户端。与正向代理不同&am…...

IT行业就业趋势显示:二季度平均月薪超8千
我国的IT互联网行业在近些年来规模迅速扩大,技能和技术水平也明显提升,目前IT互联网行业已经成为社会发展中新型产业的重要组成部分,行业的人才队伍也在不断的发展壮大,选择进入入互联网行业工作的人也越来越多。 根据58同城前段…...
【毕业设计】基于Java的五子棋游戏的设计(源代码+论文)
简介 五子棋作为一个棋类竞技运动,在民间十分流行,为了熟悉五子棋规则及技巧,以及研究简单的人工智能,决定用Java开发五子棋游戏。主要完成了人机对战和玩家之间联网对战2个功能。网络连接部分为Socket编程应用,客户端…...
C#:Krypton控件使用方法详解(第十四讲) ——kryptonSeparator
今天介绍的Krypton控件中的kryptonSeparator。下面介绍控件的外观属性如下图所示:Cursor属性:表示鼠标移动过该控件的时候,鼠标显示的形状。属性值如下图所示:DrawMoveIndicator属性:表示确定移动分隔符时是否绘制移动…...
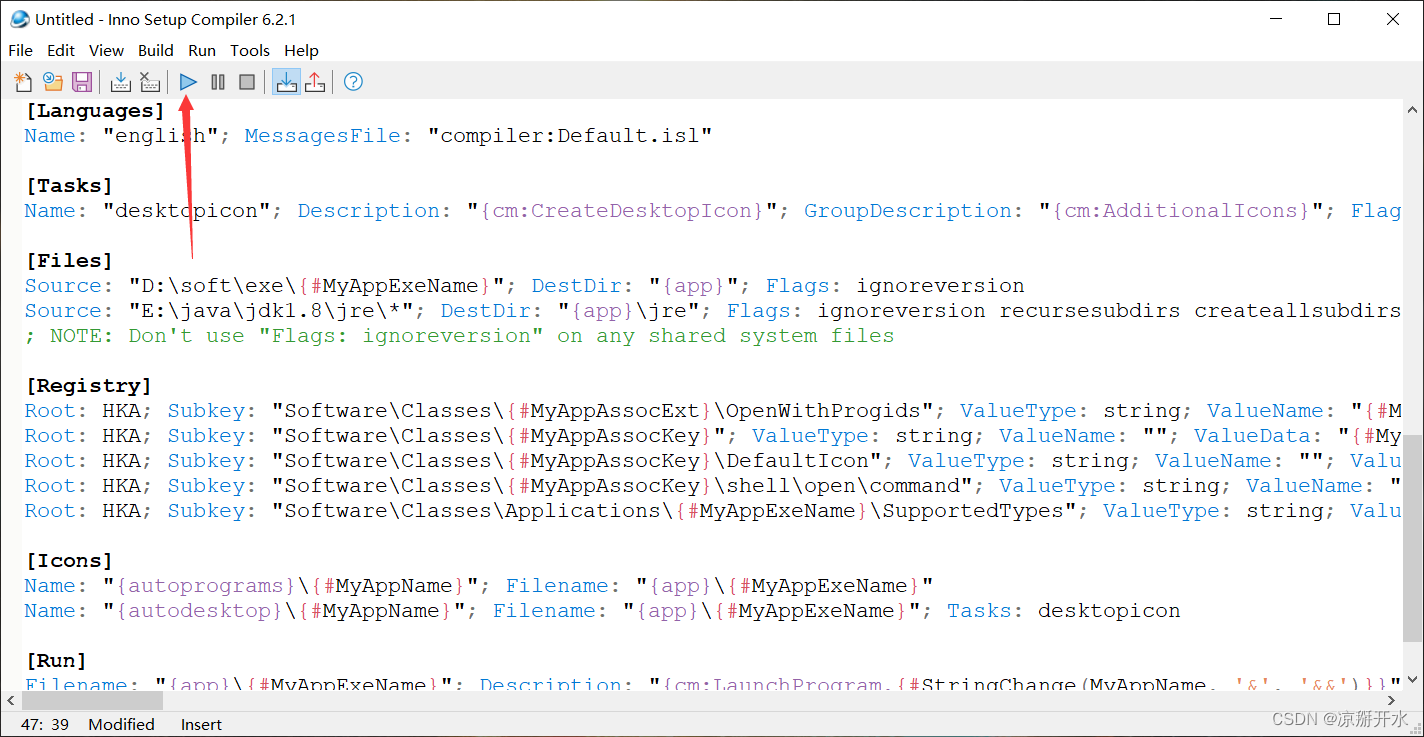
Java的jar包打包成exe应用
将springboot项目使用maven打出的jar包,打成windows平台下exe应用程序包(自带jre环境)。 工具:1、exe4j 2、Inno Setup 工具放到网盘,链接:https://pan.baidu.com/s/1ZHX8P7u-7GBxaC6uaIC8Ag 提取码&#x…...

Latex学习笔记
Latex 学习笔记 快速入门 编译软件: TeX Live TexStudio, Ctex, 线上: Overleaf第一个示例代码: \documentclass{article} % 设置文档使用的文档类 % 导言区 \title{my first Latex document} \author{Jclian91} \date{\today} \begin{document} % 正文区\maket…...
)
【c++复习】C++的基础知识(常用关键字、缺省参数、函数重载、引用)
C基础写在开头C基础常用关键字using namespace流插入和流提取操作符内联函数(inline)宏auto关键字 (c11nullptr (c11缺省参数函数重载引用写在开头 C基础部分我想介绍如下几个关键点: 常见关键字命名空间的定义和使用缺省参数函数重载引用、指针和引用的区别内联函…...

Docker入门建议收藏 第二部分
二、Docker 容器技术与虚拟机的区别 Docker 到底是个什么东西呢?我们在理解 Docker 之前,首先得先区分清楚两个概念,容器和虚拟机。 虚拟机 虚拟机(Virtual Machine)指通过软件模拟的具有完整硬件系统功能的、运行在…...

蓝桥杯三月刷题 第7天
文章目录💥前言😉解题报告💥三角回文数🤔一、思路:😎二、代码:💥数数🤔一、思路:😎二、代码:💥数组切分🤔一、思路:😎二、…...

面试官问百万数据excel导出功能如何实现?
文章目录 背景实现1.异步处理1.1 使用job1.2 使用mq2.使用easyexcel4.多个sheet5.计算limit的起始位置6.文件上传到OSS7.通过WebSocket推送通知8.总条数可配置9.order by商品编号总结背景 用户在UI界面上点击全部导出按钮,就能导出所有商品数据。 咋一看,这个需求挺简单的。…...

理解HTTPS及配置
HTTP的弊端及HTTPS的由来 众所周知HTTP协议是以TCP协议为基石诞生的一个用于传输Web内容的一个网络协议,在“网络分层模型”中属于“应用层协议”的一种.那么在这里我们并不研究该协议标准本身,而是从安全角度去探究使用该协议传输数据本身存在的安全问题:(1)、通信使用明文(不…...

IP-guard浏览器上传下载智能加解密,让管理更省心省力
现在员工日常工作中经常会通过浏览器访问公司的业务系统(OA、JIRA等),或者访问其他外部系统,访问下载服务器的文档变得更便捷,工作地点也不再局限于办公室中。为确保应用系统机密安全且又不影响员工的正常工作…...

leetcode day22 位运算
位运算咋这么老难 剑指 Offer 56 - I. 数组中数字出现的次数 借评论区大佬答案:nums [1,2,10,4,1,4,3,3] a^a0a^0aa^b^ca^c^ba&(-a)最低位为1的二进制(从又到左)所有的异或结果得到sum2^108flag-8&88可分为两组,一组为与…...
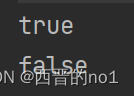
java中如何判断map是否为空
java中判断map是否为空的方法是:利用isEmpty()函数来判断。函数介绍:isEmpty()是Java中用于判断某种容器是否有元素的系统库函数。如用来判断ArrayList,HashSet,HashMap是否有元素等。在Java中,可以用isEmpty();判断一…...

C语言数据结构:链表的增删改查及动态创建
目录 一,链表与数组 ① 定义区别 ② 实现区别 二,链表遍历和计算链表中节点数量 ① 链表遍历 ② 计算节点数量 三,查找链表节点 四,增加节点到链表中 ① 在节点后方插入 ② 在节点前方插入 ● 在头节点前方插入 ● 在…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
