JS-12-es6常用知识-async
目录
1. 定义与概述
2. 使用方法
3. 注意事项
4. 应用场景
5. 示例代码
6.总结
async 是 JavaScript(包括 TypeScript)中的一个关键字,用于声明一个函数为异步函数。async其实是一个promise的语法糖,以下是关于 async 的详细解释:
1. 定义与概述
- 关键字:
async - 作用:声明一个函数为异步函数,允许函数内部使用
await关键字等待 Promise 对象的完成。 - 返回值:异步函数总是返回一个 Promise 对象,无论函数内部是否有显式的
return语句。如果没有返回语句,函数会隐式地返回一个已解析(resolved)的 Promise,其值为undefined。
2. 使用方法
-
声明:在函数定义前加上
async关键字。
async function myAsyncFunction() { // 函数体
}- 与
await配合使用:在async函数内部,可以使用await关键字等待一个 Promise 对象的完成,并获取其解析后的值。
async function fetchData() { const data = await getDataFromApi(); // 假设 getDataFromApi 返回一个 Promise console.log(data);
}3. 注意事项
-
不要单独使用:如果函数被声明为
async但没有使用await,那么该函数将没有实际异步行为,但仍然会返回一个 Promise 对象。 -
错误处理:异步函数内部可以使用
try...catch结构来捕获由await表达式抛出的错误。
async function myAsyncFunction() { try { const data = await getDataFromApi(); // 处理数据 } catch (error) { // 处理错误 }
}- 返回值:如果
async函数返回一个非 Promise 值,该值会被包装在一个已解析的 Promise 中。
4. 应用场景
- 串行处理多个异步操作:使用
async/await可以避免回调地狱和链式.then()方法带来的嵌套问题,使代码逻辑更加清晰、易于维护。 - 处理 I/O 操作:在 Node.js 中,
async/await常用于处理文件 I/O、数据库查询、网络请求等异步操作。
5. 示例代码
例1:认识
async<script>function f1() {return new Promise(resolve => {setTimeout(() => {console.log('你好');resolve();}, 1000);})}//这是上一篇文章提到的实现方法// f1().then(res=>{// console.log('第二步');// })//async的实现(async function () {//await是表示这行代码是一个异步操作//下面的代码会在这个异步操作之后执行// -->这里的异步操作执行完毕其实就是resloveawait f1();console.log('第二步');await f1();await f1();console.log('第三步');})() </script>例2:
async处理返回值。await必须是在async函数内部的
<script>function q() {return new Promise((resolve) => {setTimeout(() => {resolve("你好");}, 1000)})}//await必须是在async函数内部的var o1 = {say: async () => {console.log('say方法:');const res = await q();console.log(res);},run: async function () {console.log('run方法');const res = await q();console.log(res);}}//需求,先执行完毕say,再执行runvar fn = async function () {await o1.say();await o1.run();}fn(); </script>例3:async错误处理try...catch
<script>function q(){return new Promise((resolve,reject)=>{setTimeout(()=>{reject("你好");},100)})}(async function(){try{let res = await q();console.log(res);}catch(e){console.log(e);}})() </script>
6.总结
- await可以执行异步操作,但是await必须在async函数内执行
- await操作可以有返回值,这个返回值表示promise操作成功的返回值
- 如果await里面执行的异步操作发生了reject,或者发生了错误,那么只能使用try...catch语法来进行错误处理
相关文章:

JS-12-es6常用知识-async
目录 1. 定义与概述 2. 使用方法 3. 注意事项 4. 应用场景 5. 示例代码 6.总结 async 是 JavaScript(包括 TypeScript)中的一个关键字,用于声明一个函数为异步函数。async其实是一个promise的语法糖,以下是关于 async 的详细…...

使用winscp 通过中转机器(跳板机、堡垒机)密钥远程连接服务器,保姆级别教程
1.winscp下载地址 winscp下载 2.安装自己选择位置 3.连接服务器 到这里,基本就是没有壁垒机的就可直接连接,传递文件 4.配置中转服务器(壁垒机、跳板机) 选择高级选项 配置utf-8的编码格式 配置中转服务器(壁垒机、跳板机) 设置中专机的密码或者私钥 配置私钥...

力扣-1984. 学生分数的最小差值
文章目录 力扣题目工程代码C实现python实现 力扣题目 给你一个 下标从 0 开始 的整数数组 nums ,其中 nums[i] 表示第 i 名学生的分数。另给你一个整数 k 。 从数组中选出任意 k 名学生的分数,使这 k 个分数间 最高分 和 最低分 的 差值 达到 最小化 。…...

激动人心的LayerDiffusion终于可以在ComfyUI中使用了
一、什么是LayerDiffusion 随着Stable Diffusion等散射模型的蓬勃发展,人工智能图形生成进入了一个崭新的阶段。我们可以仅仅通过文字提示,就可以让AI模型为我们生成逼真的图像。但是,目前主流的AI生成模型大多只能生成普通的RGB图像,对生成具有透明通道的图片能力还非常有限。…...
 方法的定义与作用)
【JVM】finalize() 方法的定义与作用
finalize() 方法的定义与作用 定义 finalize() 方法是 Java 中的一种特殊方法,定义在 java.lang.Object 类中。它在对象被垃圾回收之前由垃圾回收器调用,用于执行清理操作。 方法签名: protected void finalize() throws Throwable作用 …...

这10个前端库,帮我在工作中赢得了不少摸鱼时间!!
文章目录 前言1、dayjs2、 lodash3、 Quill4、 crypto-js5、 viewerjs6、 localforage7、 vconsole8、 uuid9、 copy-text-to-clipboard10、 classnames前言 通过高效的工具提高工作效率,从而有更多的时间来处理其他重要的任务,或者……摸鱼。没错!就是摸鱼。毕竟,提高效率…...
CentOS 7上在线安装MySQL 5.7)
(2024最新)CentOS 7上在线安装MySQL 5.7
在CentOS 7上安装MySQL 5.7并配置允许远程连接,以下是详细步骤: 1. 添加MySQL官方存储库 首先,下载并添加MySQL的官方存储库。默认情况下,添加的存储库可能会包含最新的MySQL版本(如MySQL 8.0),…...

【C++高阶】C++继承学习手册:全面解析继承的各个方面
📝个人主页🌹:Eternity._ ⏩收录专栏⏪:C “ 登神长阶 ” 🤡往期回顾🤡:模板进阶 🌹🌹期待您的关注 🌹🌹 继承 📖1. 继承的概念及定义…...

使用GPT-soVITS再4060下2小时训练声音模型以及处理断句带来的声音模糊问题
B站UP主视频 感谢UP主“白菜工厂1145号员工”的“熟肉”,我这篇笔记就不展示整一个训练和推理流程,重点写的4060该注意的一些事项。如何解决断句模糊的问题,在本篇笔记的最末尾。 相关连接: 原项目github UP主的说明文档 1、训…...
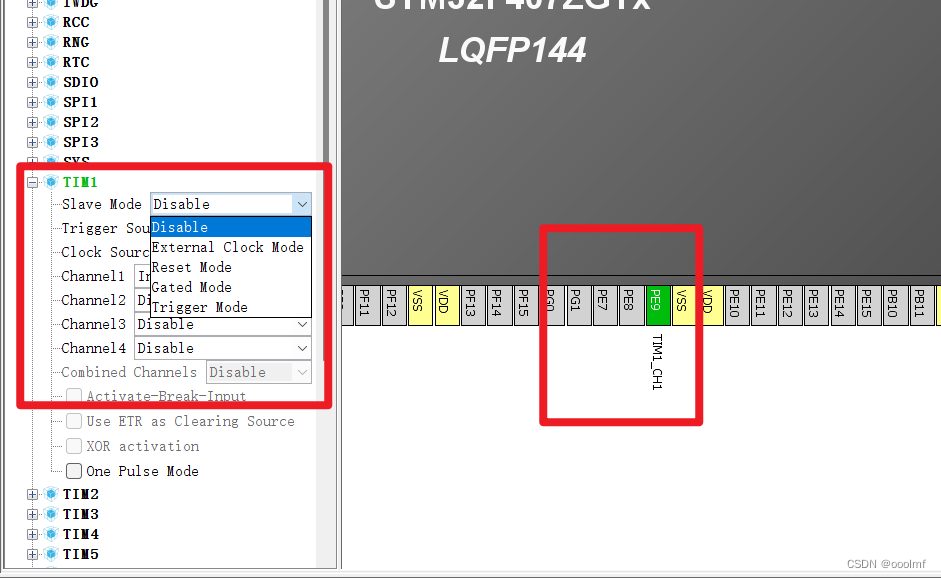
如何对stm32查看IO功能。
有些同学对于别人的开发板的资源,或者IO口,或者串口等资源不知道怎么分配。 方法1、看硬石、野火、正点原子的开发板,看下他们的例子,那个资源用什么。自己多看几个原理图,多看几个视频,做一下笔记。以后依…...
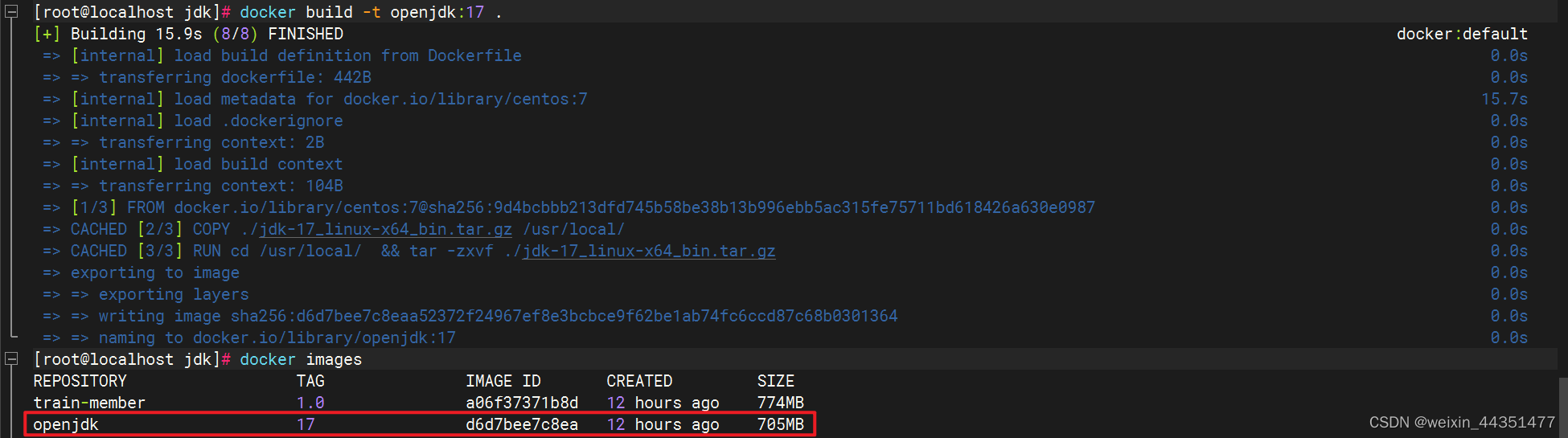
docker构建jdk17镜像
资料参考 参考自黑马教程:10.Docker基础-自定义镜像_哔哩哔哩_bilibili 更多详细语法声明,请参考官网文档:https://docs.docker.com/engine/reference/builder 初步准备 1、下载jdk17包(linux版),我这边版…...
Android Uri转File path路径,Kotlin
Android Uri转File path路径,Kotlin /*** URI转化为file path路径*/private fun getFilePathFromURI(context: Context, contentURI: Uri): String? {val result: String?var cursor: Cursor? nulltry {cursor context.contentResolver.query(contentURI, null…...
iOS界面设计要点:四大模块解析
UI设计不是艺术设计,这限制了我们从设备和现有技术开始设计。因此,熟悉每个平台的设计规则已经成为每个设计师的第一课,也是每个设计师必要的专业知识。 今天小边给您带来了iOS设计规范,希望帮助您快速熟悉iOS平台设计规范&#…...
实验课II)
数字取证技术(Digital Forensics Technology)实验课II
数字取证技术(Digital Forensics Technology)实验课II 本文是我本学期的教学课题目,不包含任何博客知识分享,无关的读者可忽略; 实验练习题 (♞思考):请对工作邮件进行签名;“problem3_1.txt"里存储的是由John Doe撰写的真实的邮件,而"problem3_2.txt"里存储的…...
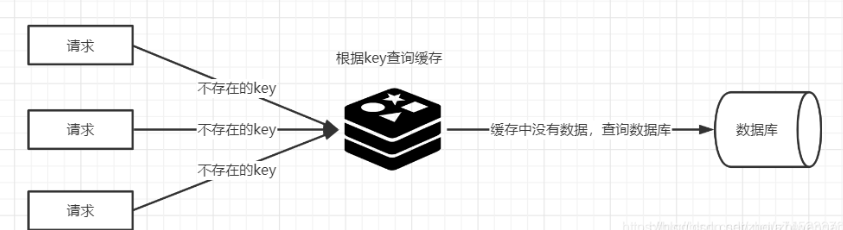
Redis缓存的使用
1.缓存穿透 描述:查询数据在redis不存在,请求打到数据库 解决方法: 缓存空值 当出现Redis查不到数据,数据库也查不到数据的情况,我们就把这个key保存到Redis中,设置value"null",并设…...

力扣LCP 08.剧情触发时间
力扣LCP 08.剧情触发时间 前缀和 二分 对increase求前缀和 在前缀和数组上做二分 找到符合要求的最小时间 class Solution {public:vector<int> getTriggerTime(vector<vector<int>>& increase, vector<vector<int>>& requirements)…...

Elasticsearch-IndexTemplate和DynamicTemplate 有什么区别
Elasticsearch中的Index Template和Dynamic Template是两种不同的概念,它们在索引管理中扮演不同的角色: ### Index Template(索引模板) 1. **目的**:用于定义新索引的默认设置,包括映射、设置、别名等。 …...
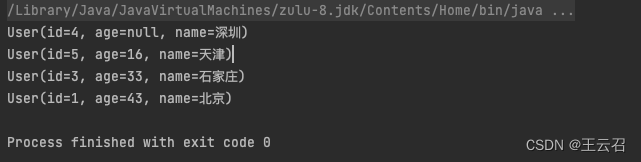
list集合自定义排序
一、基本类型排序 1.list中只有数字或字符串 //升序排序 List<T> ,T为数字或字符串 Collections.sort(list); //降序排序 Collections.sort(list,Collections.reverseOrder());2.list中为对象 基于jdk.18 import lombok.Data;Data public class User {private int i…...

PHP Cookies:应用与管理
在Web开发中,Cookies是一种在客户端(通常是浏览器)存储少量数据的机制。PHP作为一种服务器端脚本语言,提供了对Cookies的全面支持,使得开发者可以轻松地设置、读取和删除Cookies。Cookies通常用于存储用户的会话信息&a…...
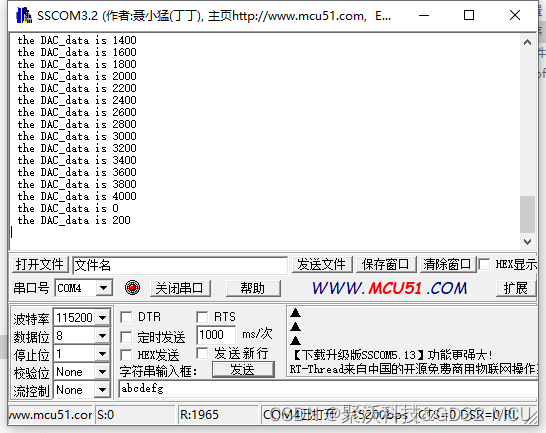
【GD32F303红枫派使用手册】第十四节 DAC-输出电压实验
14.1 实验内容 通过本实验主要学习以下内容: DAC工作原理 使用DAC输出电压 14.2 实验原理 14.2.1 DAC工作原理 我们上几章学习了ADC,本章我们来学习DAC。ADC是模-数转换,即模拟量转换为数字量,DAC正好相反,即数-…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...
