中心极限定理的MATLAB例
独立同分布的中心极限定理:
设 X 1 , X 2 , … , X n X_1, X_2, \ldots, X_n X1,X2,…,Xn 是独立同分布的随机变量序列,且 E ( X i ) = μ E(X_i) = \mu E(Xi)=μ, D ( X i ) = σ 2 > 0 D(X_i) = \sigma^2 > 0 D(Xi)=σ2>0,则随机变量之和 ∑ i = 1 n X i \sum_{i=1}^{n}X_i ∑i=1nXi 的标准化变量 ∑ i = 1 n X i − n μ n σ \frac{\sum_{i=1}^{n}X_i - n\mu}{\sqrt{n}\sigma} nσ∑i=1nXi−nμ 的分布函数 F n ( x ) F_n(x) Fn(x) 对于任意 x x x 满足 lim n → ∞ F n ( x ) = Φ ( x ) \lim_{{n \to \infty}} F_n(x) = \Phi(x) limn→∞Fn(x)=Φ(x),其中 Φ ( x ) \Phi(x) Φ(x) 是标准正态分布的分布函数。
简单来说,中心极限定理表明,当从任意一个总体中抽取样本量足够大的样本时,样本均值的分布将趋近于正态分布,无论原来的总体分布是什么。
mu = 1; % Population parameter
n = 1e3; % Sample size
ns = 1e4; % Number of samples
%%
rng('default') % For reproducibility
samples = exprnd(mu,n,ns); % Population samples
means = mean(samples); % Sample means
%%
[muHat,sigmaHat] = normfit(means);
numbins = 50;
%%
figure
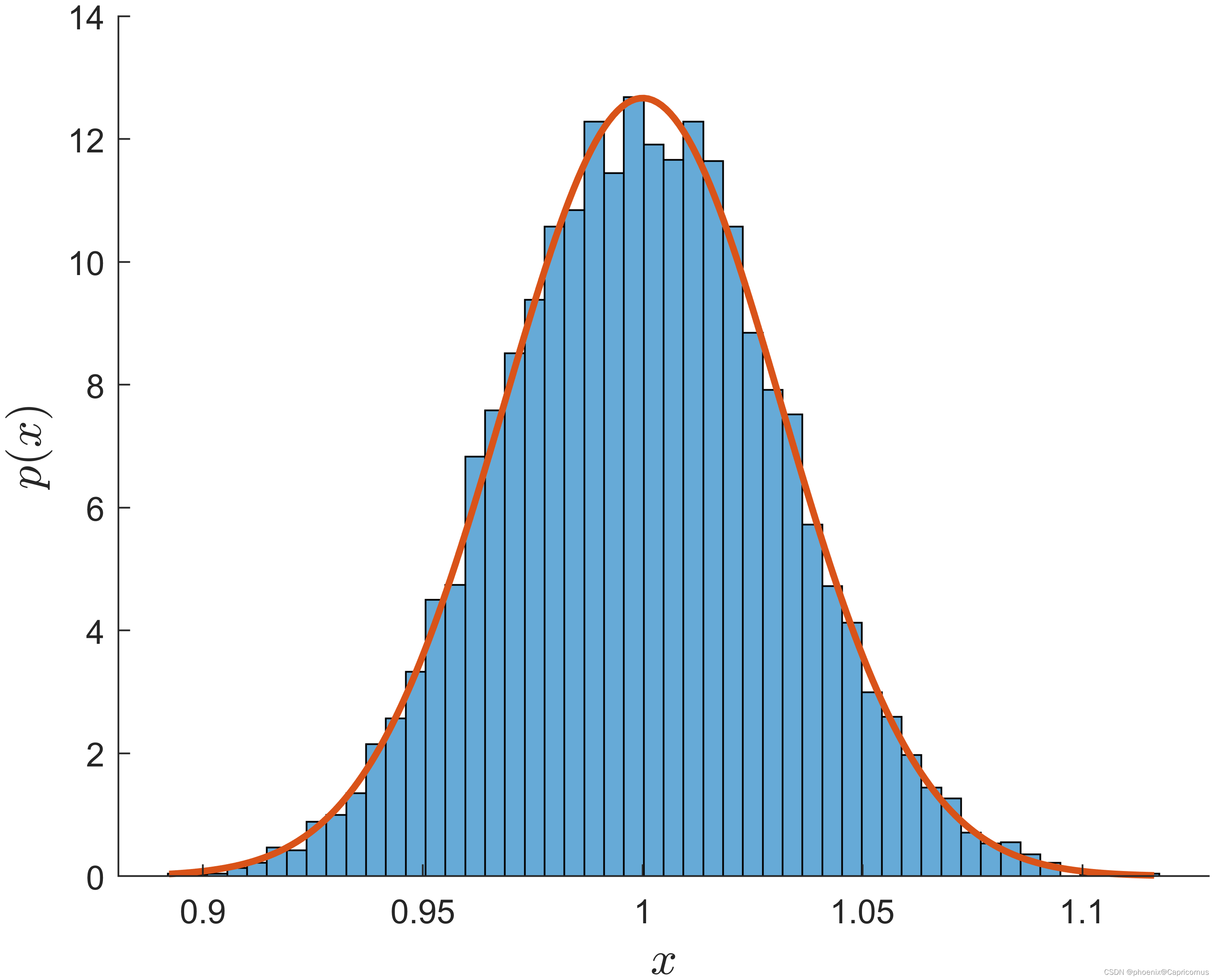
histogram(means,numbins,'Normalization','pdf')
hold on
x = min(means):0.001:max(means);
y = normpdf(x,muHat,sigmaHat);
plot(x,y,'LineWidth',2)
box off
xlabel('$x$', 'FontSize',14, 'Interpreter','latex')
ylabel('$p(x)$', 'FontSize',14, 'Interpreter','latex')
相关文章:

中心极限定理的MATLAB例
独立同分布的中心极限定理: 设 X 1 , X 2 , … , X n X_1, X_2, \ldots, X_n X1,X2,…,Xn 是独立同分布的随机变量序列,且 E ( X i ) μ E(X_i) \mu E(Xi)μ, D ( X i ) σ 2 > 0 D(X_i) \sigma^2 > 0 D(Xi)σ2>0&a…...

定义input_password函数,提示用户输入密码.如果用户输入长度<8,抛出异常,如果用户输入长度>=8,返回输入的密码
def input_password(password):str1passwordlen1len(str1)try:if len1<8:raise ValueError("密码长度不能小于8")else:return print(f"你的密码为:{password},请确认")except ValueError as e:print(f":Error is {e}")number1input("请…...

【深度学习】IP-Adapter 和 InstantID 的核心机制比较
IP-Adapter 和 InstantID 是两个在图像生成中具有不同优势和应用场景的模型。以下是这两个模型的区别及其理论分析。 IP-Adapter 特点: 图像提示能力: IP-Adapter 通过引入图像提示能力,使得预训练的文本到图像扩散模型可以接受图像作为提示,从而生成…...
JEPaaS 低代码平台 j_spring_security_check SQL注入漏洞复现
0x01 产品简介 JEPaaS是一款优秀的软件平台产品,可视化开发环境,低代码拖拽式配置开发,操作极其简单,可以帮助解决Java项目80%的重复工作,让开发更多关注业务逻辑,大大提高开发效率,能帮助公司大幅节省人力成本和时间成本,同时又不失灵活性。适用于搭建 OA、ERP、CRM、…...

天锐绿盾 | 无感知加密软件、透明加密系统、数据防泄漏软件
摘要:文件加密软件,包含禁止非授权的文件泄密和抄袭复制解决方案即使被复制泄密都是自动加密无法阅读,透明加密,反复制软件,内网监控,文件加密,网络安全方案,透明文件加密,加密文件,图纸加密,知识产权保护,加密数据; 通过绿盾信息安全管理软件,系统在不改…...
kubernetes(k8s)集群部署(2)
目录 k8s集群类型 k8s集群规划: 1.基础环境准备: (1)保证可以连接外网 (2)关闭禁用防火墙和selinux (3)同步阿里云服务器时间(达到集群之间时间同步) &…...

Git操作指南
1、提交代码操作 拉取线上分支,防止本地代码提交冲突 git pull origin dev git add . git commit -m “给本次提交添加注释” git push origin dev 2、打分支并切换分支 git checkout -b 新建并切换到新分支 切换到主分支 git checkout main git merge dev git p…...

全域推广和标准推广哪个更好。谁更容易获客?
随着全域概念的兴起,全域推广逐渐走进人们视野,并成为新的互联网热词。在此背景下,与全域推广相关的话题,如全域推广是什么及全域推广和标准推广的区别等成为了许多创业者讨论和搜索的对象。 所谓的全域推广,简单来说…...

首张地下地图!D-Wave 专用量子计算机助力沙特阿美完成地震成像
内容来源:量子前哨(ID:Qforepost) 文丨浪味仙 排版丨沛贤 深度好文:800字丨3分钟阅读 摘要:过去两年中,沙特阿美研究中心一直在使用总部在加拿大的D-Wave 公司的专用量子计算技术,…...
机器学习分类及算法
1. 深度学习 1.1学习算法 1.2基本术语和概念 1.3机器学习分类常用算法 1.3.1线性回归 1.3.2逻辑回归 1.3.3决策树 1.3.4朴素贝叶斯 1.3.5支持向量机SVM 1.3.6K-最近临邻KNN 还有K-均值(k-means)、随机森林、降维、人工神经网络等 1.4超参数和验证集 1.4.…...

电容器连接到 PCB 电源层的过孔配置
为什么我们需要去耦电容器? 时钟数字IC通常需要大的瞬态电源电流。例如,大型微处理器可以在很短的时间内消耗高达 10 A 的电流。随着 IC 输出的上升/下降时间缩短,我们需要以更高的速率提供瞬态能量。PCB 的电源和接地导体确实存在一定的电感…...
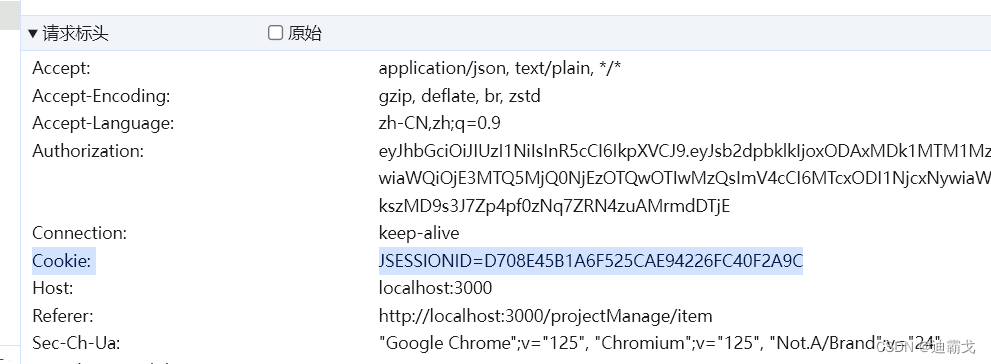
springboot+shiro+jwt 兼容session和token
最近和别的软件集成项目,需要提供给别人接口来进行数据传输,发现给他token后并不能访问我的接口,拿postman试了下还真是不行。检查代码发现项目的shiro配置是通过session会话来校验信息的 ,我之前一直是前后端自己写,用…...
)
CSS Display(显示)
CSS Display(显示) 概述 CSS(层叠样式表)中的display属性是控制元素如何显示的关键属性。它决定了元素的盒模型类型,即元素是块级元素、内联元素还是其他类型的元素。display属性对于网页布局和元素样式的控制至关重要。 基本用法 块级元…...
【PB案例学习笔记】-20制作一个超链接按钮
写在前面 这是PB案例学习笔记系列文章的第19篇,该系列文章适合具有一定PB基础的读者。 通过一个个由浅入深的编程实战案例学习,提高编程技巧,以保证小伙伴们能应付公司的各种开发需求。 文章中设计到的源码,小凡都上传到了gite…...

Django中使用下拉列表过滤HTML表格数据
在Django中,你可以使用下拉列表(即选择框)来过滤HTML表格中的数据。这通常涉及两个主要步骤:创建过滤表单和处理过滤逻辑。 创建过滤表单 首先,你需要创建一个表单,用于接收用户选择的过滤条件。这个表单可…...
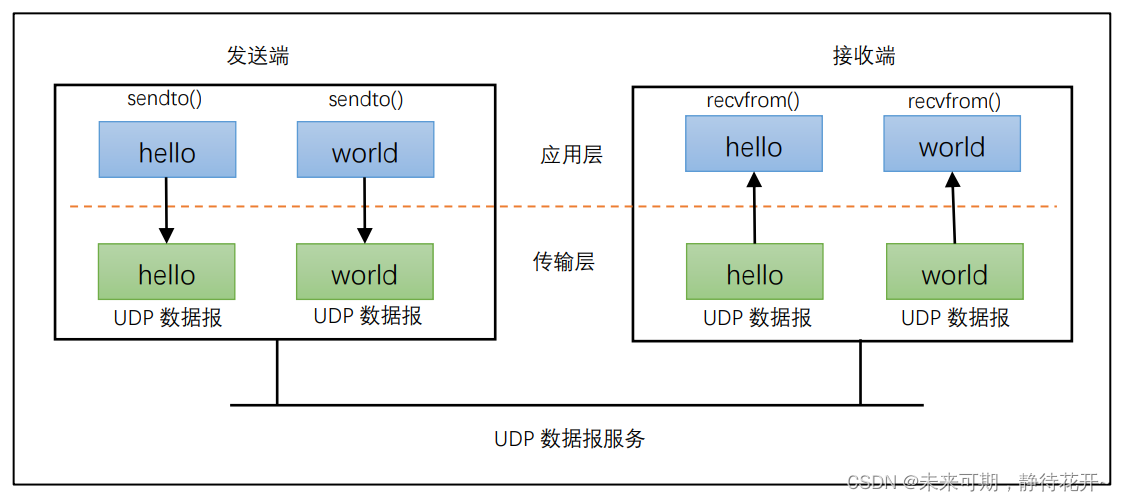
Linux基础 (十五):TCP 协议特点和UDP协议
上一节,我们学习了TCP协议的服务器-客户端的编程流程以及对中间的过程进行了详细的讨论,那么,这一节,我们对于TCP协议的特点进行进一步的分析,这也是面试的重点和难点。 目录 一、TCP 协议特点 1.1 连接的建立与断…...

python替换word文件中的图片
python替换word文件中的图片 模拟鼠标键盘,截屏 import glob import os import timeimport pyautogui import pyautogui as p from PIL import ImageGrab from pynput.keyboard import Controller# -*- coding:utf-8 -*-directory ./directory1 ./outputfor f i…...
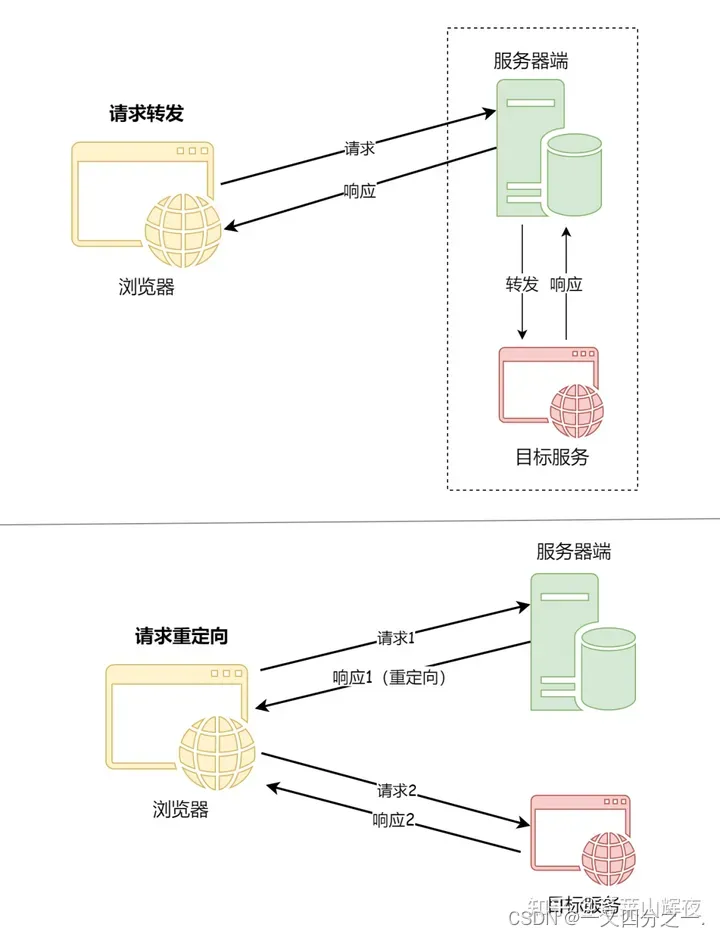
Servlet-01
文章目录 Servlet创建Servlet探究Servlet的生命周期 HttpServletWebServlet注解详解 重定向与请求转发ServletContextServletContext中的接口 HttpServletRequestHttpServletResponse状态码解释Cookie Servlet Q:它能做什么呢? A:我们可以通…...

C语言:链表
链表 介绍单向链表节点结构创建节点插入节点删除节点遍历链表尾部插入查找节点链表反转示例程序程序1程序2 介绍 链表是一种常见的数据结构,用于存储一系列线性数据。与数组不同,链表中的元素在内存中不必是连续存放的,而是通过指针将每个元…...
【git使用二】gitee远程仓库创建与本地git命令用法
目录 gitee介绍 管理者注册gitee账号 管理者在gitee网站上创建远程仓库 每个开发者安装git与基本配置 1.git的下载和安装 2.配置SSH公钥 3.开发者信息配置 git命令用法 gitee介绍 Gitee(又称码云)是一个基于Git的代码托管服务,由开源…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

【Redis】Redis从入门到实战:全面指南
Redis从入门到实战:全面指南 一、Redis简介 Redis(Remote Dictionary Server)是一个开源的、基于内存的键值存储系统,它可以用作数据库、缓存和消息代理。由Salvatore Sanfilippo于2009年开发,因其高性能、丰富的数据结构和广泛的语言支持而广受欢迎。 Redis核心特点:…...
